Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante.

 

QUESTO il quiz di cui questo articolo costituisce la soluzione

 

Premessa (per i meno esperti)

I fotoni sono le particelle-non particelle che trasportano la luce e riescono a esistere solo viaggiando alla massima velocità possibile, quella della luce, appunto. In realtà, se non corressero, non avrebbero massa e sparirebbero nel nulla: chi ha visto un fotone fermo alzi la mano! Senza di loro non si vedrebbe niente…e tutto sarebbe buio e triste.

I fotoni sono le “particelle” più allegre dell’Universo, essendo libere di muoversi e di scontrarsi con i loro grandi amici elettroni, che a volte li seguono nel loro girovagare continuo, altre volte no, ma il divertimento è sempre assicurato. Chi non ci crede vada a leggere la QED e/o la fisica papalliana…

Tra di loro non esiste invidia o gelosia, dato che sono tutti uguali, malgrado possano cambiare colore ed energia a seconda del balletto che compiono mentre viaggiano. Sappiamo già che, a volte, questo cambio di colore è del tutto apparente, ma il risultato è sempre estremamente fantasioso e apprezzato da tutti i corpi celesti. Fare apparire le cose come non sono in realtà… ecco un gioco che a loro piace moltissimo e di cui anche gli uomini sono consapevoli (aberrazione, effetto doppler, miraggi, fate morgane e mille altre diavolerie del genere). In particolare, si divertono a prendere in giro quel sapientone di Albertino (il mago che avete conosciuto QUI). Gli vogliono un gran bene, tanto che gli hanno regalato perfino un Premio Nobel (effetto fotoelettrico), ma fanno di tutto per metterlo in agitazione e in difficoltà, combinandogli scherzi insospettabili. Poi tutto finisce con una bella risata…

Albertino si vanta tanto (e giustamente) della sua Relatività Ristretta e non perde occasione per farsi bello e dimostrare che può spiegare praticamente tutto (compresa la strana massa dei fotoni, che proprio massa non è). E allora è proprio su questa teoria inattaccabile che scatenano la loro fantasia.

A volte, però, la cosa capita quasi senza volerlo.

Si tramanda una storia molto simpatica che vede come attori principali due amici per la pelle, il fotone A e il fotone B, destinati a vivere separati ai due estremi di un righello di lunghezza d₀. In realtà, loro non vivono da fermi, ma possono facilmente essere creati in un certo posto e a un certo tempo. Il discorso non è facile da spiegare, ma a noi interessa poco in questa avventura, ormai diventata celebre nel mondo fotonico. Immaginiamo, quindi, che A e B esistano potenzialmente nei due estremi del righello, pronti a nascere e spiccare il volo. Ovviamente, sul righello vi sono moltissimi altri fotoni potenziali (anche nella stessa posizione di A e di B), pronti a partire continuamente. In altre parole, dato che i fotoni trasportano la luce, il righello è sempre illuminato. Ma noi interessa soltanto (per adesso) la storia dei due amici per la pelle.

Una favola molto reale

Tutto nasce proprio da Albertino che, ancora una volta, vuole dimostrare quanto bella e perfetta sia la sua teoria. Lui ha preso un righello (proprio il loro righello) e ha deciso di farlo muovere a grande velocità, poco meno di quella a cui viaggiano normalmente i fotoni. Come previsto il righello si accorcia (e i potenziali fotoni A e B si avvicinano) e tutte le misure eseguite da chi sta fermo rispetto al righello non possono che confermarlo. Ancora una volta Albertino ha stupito il mondo! La nuova lunghezza d è minore di d₀. Questo momento di stupore e ammirazione è rappresentato in Fig. 1.

“Come sarebbe bello farci fotografare mentre viaggiamo a questa velocità” pensano i due fotoni. Bastava che venissero eccitati, sarebbero nati e si sarebbero lanciati verso la macchina fotografica M e sarebbero apparsi entrambi nella fotografia. Una bella foto, con i due fotoni agli estremi e il righello accorciato che li unisce, segnalato da tutti gli altri amici dislocati lungo l’asta.  Sarebbero stati molto più vicini!

A e B erano già stati fotografati, ma con il righello fermo, ossia con una distanza tra di loro uguale a d₀. Loro sapevano bene come fare… partiva il fotone A, mentre il fotone B aspettava che A arrivasse a una distanza dalla macchina fotografica M uguale alla sua; poi partiva anche B che sarebbe giunto insieme all’amico nello stesso istante t₀, quello del “clic” della macchina fotografica (viaggiando alla stessa velocità e avendo lo stesso spazio da percorrere, sarebbe stato uguale anche il tempo impiegato). Un lavoro di “routine” che conoscevano molto bene.

L’importante era che A partisse a un certo tempo t_A e che B partisse un po’ dopo, al tempo t_B. Ripetiamo: se B partisse insieme ad A, arriverebbe su M molto prima dell’amico, dato che la distanza BM è più corta di AM e loro viaggiano alla stessa velocità (come già detto, non possono rallentare). B doveva, perciò, aspettare che la distanza tra l’amico A e M diminuisse fino a diventare uguale alla sua.

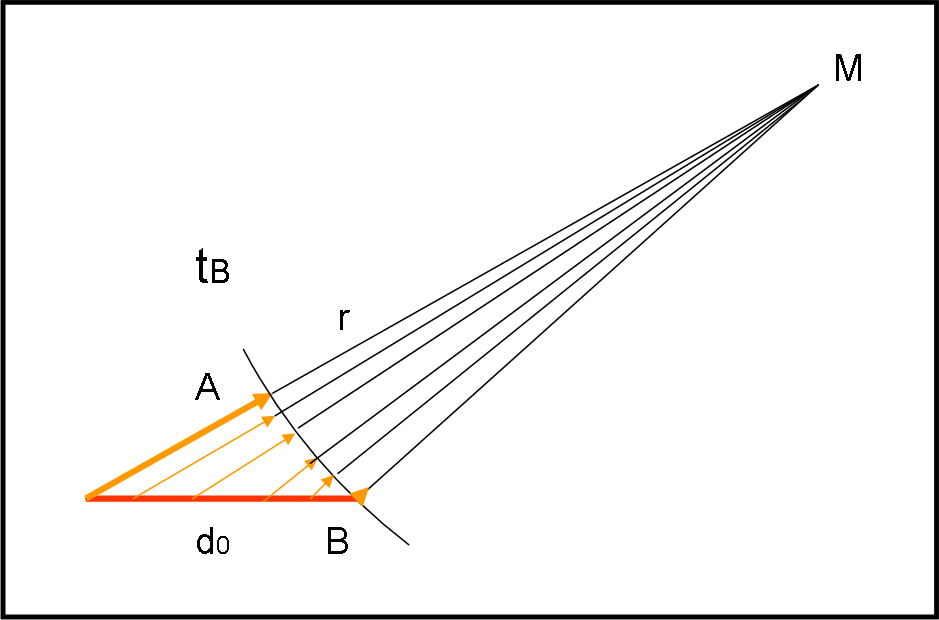
Ovviamente non erano solo loro a fare quel gioco. In ogni istante, dal righello partivano dei fotoni diretti verso M, ma, ovviamente, alcuni arrivavano in M prima, altri dopo, del tempo t₀. Solo quelli che si accodavano al viaggio di A, partendo quando la distanza tra loro ed M era uguale a quella di A da M avrebbero raggiunto insieme ad A e B la macchina fotografica nel momento t₀ dello scatto. La Fig. 2 ci mostra una serie di fotoni del righello che sono partiti ai tempi giusti (compresi tra t_A e t_B), in modo da essere, al tempo t_B, tutti alla stessa distanza da M. Questi fotoni, compresi tra A e  B, sono gli unici che saranno visibili nell’immagine ripresa da M all’istante t₀. Ovviamente la distanza tra A e B rimane sempre la stessa, ossia d₀.

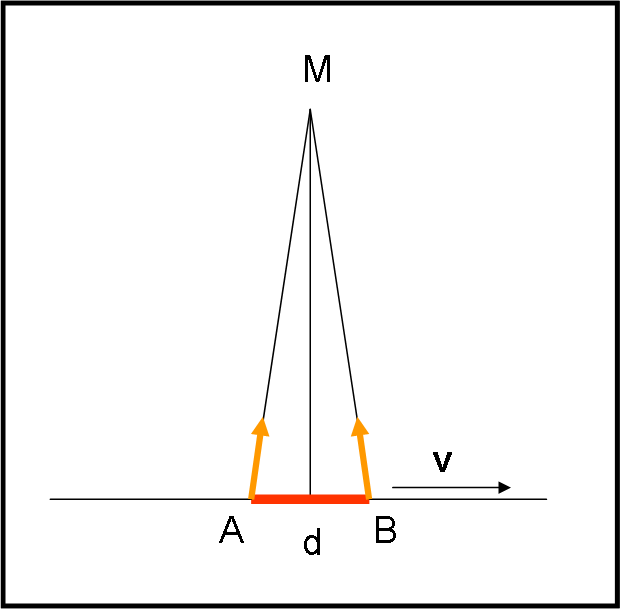
A e B sono così amici che il solo pensiero di avvicinarsi li emoziona. Il righello sta viaggiando a una certa velocità v e il fotone A si fa coraggio e decide che è il momento di partire verso la macchina fotografica M: sarebbe arrivato da lei proprio nel momento t₀ stabilito per lo scatto istantaneo (la foto avrebbe ripreso solo ciò che sarebbe arrivato da lei in quel momento esatto: chi c’è c’è e chi non c’è non c’è!).

Il fotone B scalpita per partire anche lui, ma sa che non può farlo subito, come già detto precedentemente e come mostra il primo riquadro della Fig. 3, a partire dall’alto.

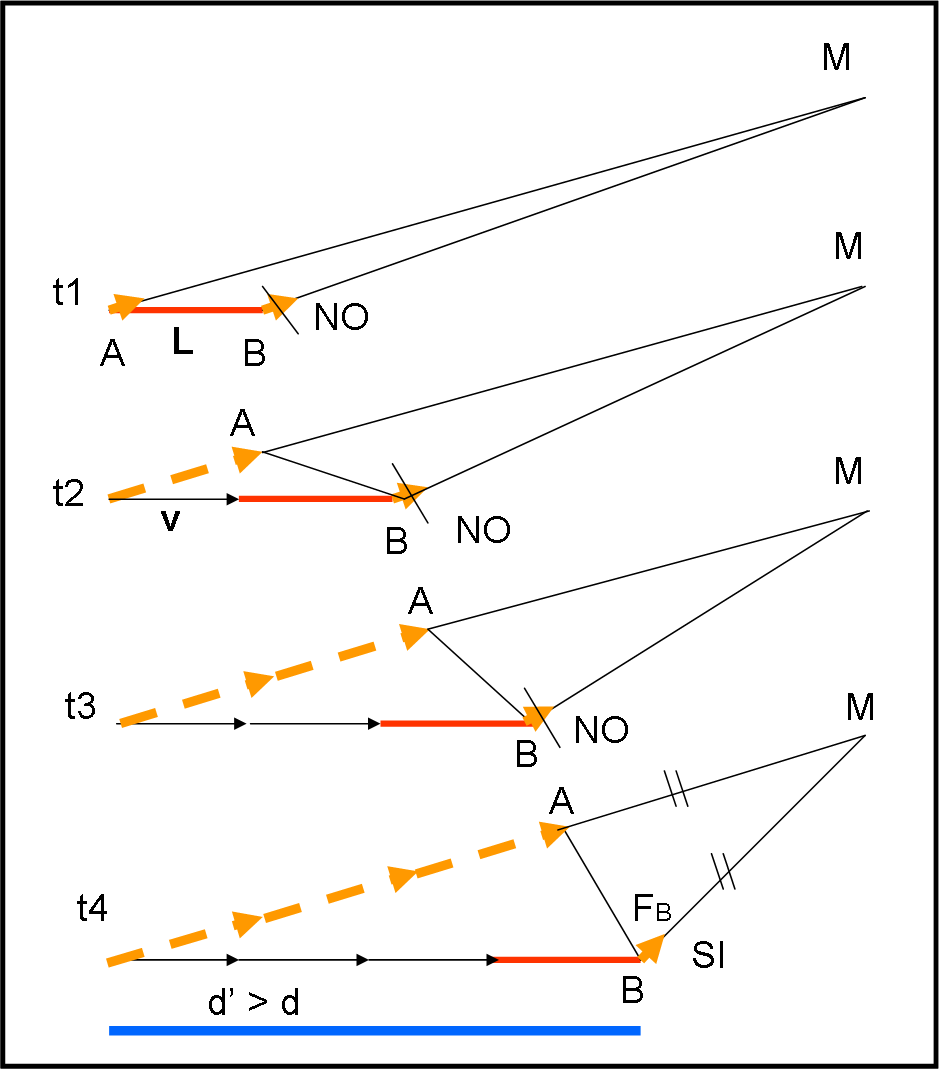
Lascia passare un secondo (di solito bastava…) e rifà la sua misura: accidenti, è sempre più avanti di A. La spiegazione è facile: mentre A ha percorso la freccia gialla tratteggiata, lui si è mosso verso destra con una velocità v, non molto più piccola di quella della luce, ossia la loro. B deve ancora aspettare (secondo riquadro dall’alto della Fig. 3). Potesse farlo, B sarebbe tutto sudato…

Passa un altro secondo e la situazione è quella del terzo riquadro della Fig. 3. B comincia a rincuorarsi. Si è accorto, infatti, che la differenza tra il percorso che deve fare lui per arrivare a M diventa sempre più simile a quello che manca ad A per arrivare alla macchina fotografica nello stesso istante t₀. Comincia ad eccitarsi e si prepara al volo. Ormai è questione di poco…

Un altro secondo è trascorso (ma poteva anche essere di meno…) e la configurazione diventa quella dell’ultimo riquadro in basso. Non c’è più dubbio: la distanza tra A, già in viaggio da un po’, ed M è ormai perfettamente uguale alla distanza tra B ed M. E’ il momento di partire, dato che uguale distanza e uguale velocità vogliono anche dire tempo uguale. A e B arriveranno sicuramente su M nello stesso istante t₀, come se si dessero la mano. E così avviene!

Perfetto, A e B sono sicuri di essere stati immortalati nella foto e sono anche sicuri che appariranno più vicini di quando il righello era fermo, dato che Albertino ha dimostrato attraverso misure precise che la lunghezza si è accorciata.

Pochi attimi e possono guardare la foto… Accidenti, questa non se la aspettavano (e nemmeno Albertino che diventa bianco in volto). La distanza tra A e B (che si vedono benissimo nella foto, essendo agli estremi del righello) è molto più grande di quella prevista (e misurata) da Albertino, ma anche di quella che era all’inizio, prima di essere accorciata.

Un attimo di ragionamento e tutto appare chiaro: la posizione di A, sulla pellicola fotografica, si riferisce all’istante t₁ in cui è partito. La posizione di B si riferisce, invece, all’istante in cui B ha lasciato il righello, ossia quella relativa al tempo t₄. In poche parole, ciò che si vede nella fotografia è A nella posizione del primo riquadro e B nella posizione del quarto riquadro, ossia tra loro sembra proprio che la distanza sia quella disegnata in azzurro.

Albertino è distrutto, mentre i due fotoni sono ancora un po’ frastornati, ma stanno capendo tutto e sanno anche come fare per ottenere il loro sogno. Lo dicono subito ad Albertino e anch’egli si rincuora. L’accorciamento del righello esiste davvero e può essere misurato, ma la sua visione apparente è ben diversa dalla realtà misurata.

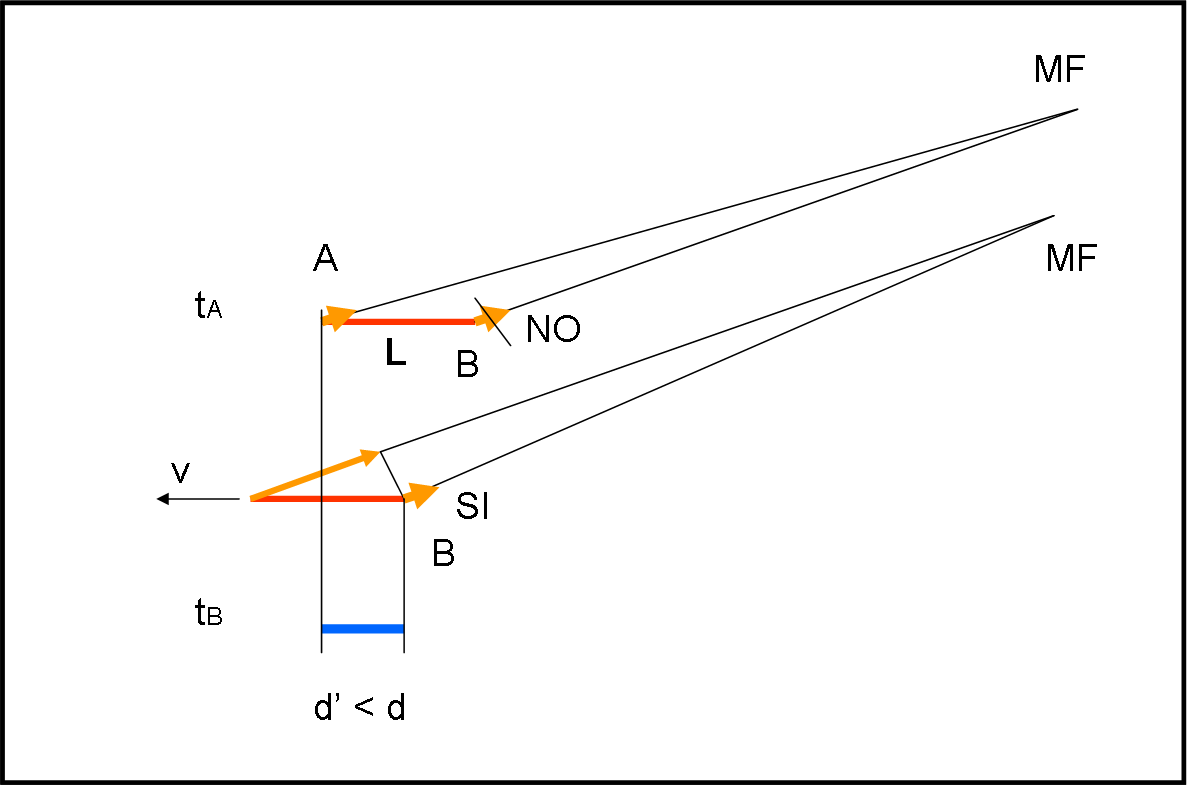
I due amici propongono ad Albertino di fare di nuovo l’esperimento, ma facendo andare il righello alla stessa velocità, ma in verso opposto. Albertino ha ormai capito anche lui e la sua bocca si curva in un sorriso. Come ormai previsto, la nuova foto dà un risultato del tutto opposto: il righello si è accorciato moltissimo ed è addirittura più corto di quanto previsto e misurato da Albertino (Fig. 4). Ma ormai tutti e tre hanno capito il perché e il percome e non possono che brindare tutti assieme con un bel bicchiere di vino (non accorciato…).

Parliamo seriamente e capiamo che una cosa è misurare e un’altra cosa è vedere…

La realtà apparente e quella misurata

La teoria della Relatività Ristretta non è certo “distrutta” da questa favola reale inventata da quei mattacchioni dei fotoni. Tutto, in fondo, si basa sulla “finitezza” della velocità della luce che può dar luogo a configurazioni istantanee nella vita quotidiana, ma che non sono più tali se le distanze da percorrere sono ben più grandi. In generale, nell’articolo di “aiuto”, avevamo già dimostrato che fotografare oggetti in movimento (anche non rapidissimo) comporta un visione apparente ben lontana dalla realtà dei fatti, allorché la luce prima di giungere a noi dia il tempo ai vari oggetti di spostarsi in modo evidente.

Tuttavia, anche oggetti posti vicini a noi possono dar luogo a configurazioni del tutto inaspettate, se le velocità con cui si spostano diventano comparabili con la velocità della luce. In modo analogo a prima, nel tempo che la luce impiega per partire da un punto di un oggetto e giungere alla macchina fotografica, l’oggetto stesso si è spostato macroscopicamente e la luce che deve giungere alla macchina, da un altro punto dell’oggetto, allo stesso tempo t₀, proviene da una posizione ben diversa da quella originaria. In fondo è ciò che abbiamo mostrato con la favola. Il fotone che vuole arrivare insieme all’amico deve partire dopo e questo tempo si allunga se si è allontanato a grande velocità dal punto originario. Ciò che fotografiamo al singolo tempo t₀ corrisponde a due fotoni partiti in tempi decisamente diversi.

Abbiamo, perciò, un qualcosa che si aggiunge agli effetti della RR per quanto riguarda l’apparenza visiva (o meglio fotografica) delle dimensioni di un oggetto. Siamo sempre in ambito relativistico, ma certi risultati teorici ineccepibili vengono profondamente trasformati nella realtà visibile.

Il caso del righello è solo il primo e più semplice esempio di deformazione apparente di una lunghezza. Abbiamo visto che deriva dalla finitezza della velocità della luce, ma intuiamo facilmente anche che la deformazione è fortemente dipendente dalla direzione della velocità dell’oggetto rispetto alla macchina fotografica. In qualche modo, possiamo concludere che la lunghezza del righello è estremamente variabile e non è certo quella che ci aspetteremmo dalla RR. Va, quindi, capita bene la differenza.

La contrazione delle lunghezze rimane un dato di fatto che non viene minimamente scalfito. Se in un sistema di riferimento in quiete eseguo le misurazioni atte a stabilire la lunghezza del righello, non posso che confermare una contrazione che dipende solo e soltanto dalla velocità v dell’oggetto (come dimostra il fattore di Lorentz). Tuttavia, se mi chiedo quanto questo effetto misurato sia realmente visibile non posso che accettare una risposta ben più complessa. La macchina fotografica è una prova inconfutabile, dato che essa ci mostra ciò che realmente si vede, comprese le deformazioni di cui si diceva prima.

Sembrerebbe una discussione poco utile se ci limitassimo a misurare la vera differenza tra due punti. Tuttavia, a volte e soprattutto con la tecnologia odierna, è proprio la fotografia che ci dona l’informazione che si deve studiare. Immaginiamo una particella che viaggi a grandissima velocità. Non è certo possibile misurare le sue dimensioni in modo standard, ma solo attraverso una serie di immagini riprese da sofisticate telecamere o da fotogrammi istantanei, fortemente influenzati dalle deformazioni che abbiamo appena cominciato ad analizzare. Lo stesso Einstein non le aveva considerate…

Una trattazione analitica

Descriviamo analiticamente il nostro caso, utilizzando un metodo basato, essenzialmente, sul solo teorema di Pitagora (ma ne esistono sicuramente di alternativi che sfruttano la trigonometria). Tuttavia, quello descritto è sicuramente il più facile da seguire ed è facilmente applicabile nei casi pratici, dato che si riduce a un’equazione di secondo grado…

Consideriamo la Fig. 5. Tracciamo da M la circonferenza che passi per la posizione di A e per quella di B all’istante t in cui deve lanciarsi anche lui. Questa circonferenza ci dice che al tempo t BM è uguale ad AM: i due fotoni arriveranno insieme in M al tempo t₀. Questa uguaglianza ci garantisce l’arrivo contemporaneo, imponendoci le condizioni perché ciò avvenga. In questo contesto l’unica incognita è il tempo t.

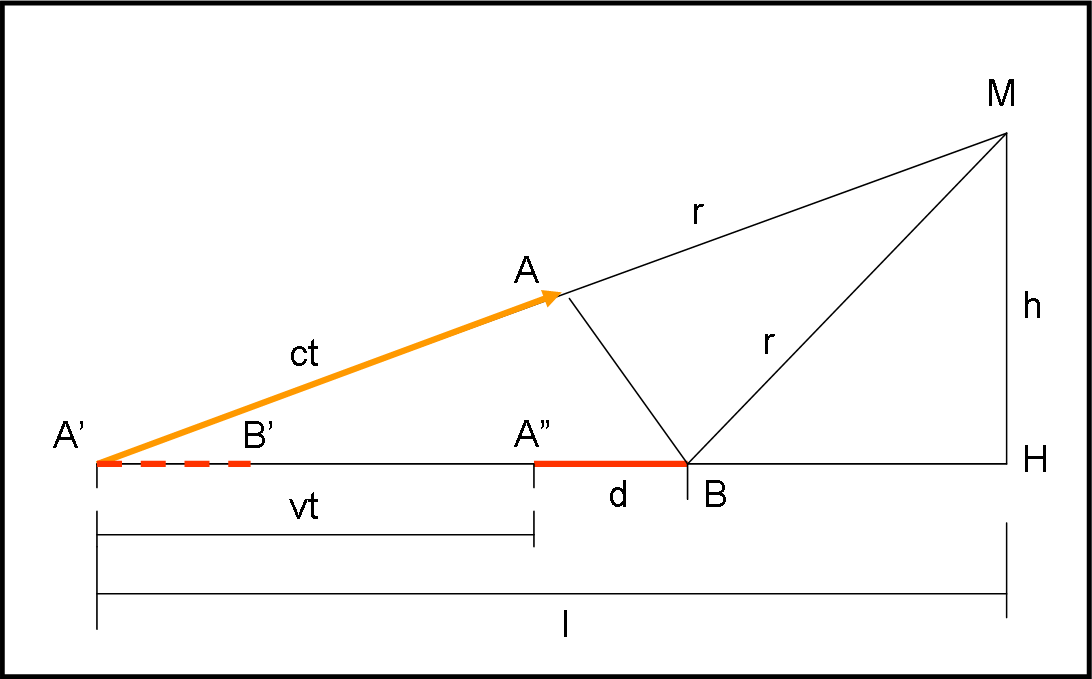
Consideriamo come origine il punto A’ da cui è partito A. Indichiamo con l e h l’ascissa e l’ordinata di M (l’asse delle ascisse è quello su cui si muove il righello di lunghezza d, già contratta).

Al tempo t, il fotone A  ha percorso una distanza che è data da:

A’A = c t

Deve ancora percorrere la distanza AM che indichiamo con r.

Ne segue che:

r = (l² + h²)^1/2 – ct

r² = l² + h² + ct² - 2 ct(l² + h²)^1/2       …. (1)

Nello stesso tempo t il righello si è spostato di vt e possiamo scrivere:

A’H = l = vt + d + BH

E ancora:

BH = l – vt – d

Da cui, applicando Pitagora al triangolo MHB:

r² = h² + (l – vt – d)²

r² = h² + l² + v²t² + d² - 2vlt - 2ld + 2vdt            …. (2)

Uguagliando la (1) e la (2), si ottiene:

l² + h² + ct² - 2 ct(l² + h²)^1/2  =  h² + l² + v²t² + d² - 2vlt - 2ld + 2vdt

Con facili passaggi (e qualche semplificazione), si ha:

ct² - 2 ct(l² + h²)^1/2  =  v²t² + d² - 2vlt - 2ld + 2vdt

t²(c²- v²)  - 2 tc (l² + h²)^1/2 + 2vlt -  2vdt  + 2dl – d² = 0

t²(c²- v²)  - 2 t [c(l² + h²)^1/2 – v (l – d)]  + 2dl – d² = 0

Sostituendo i valori noti è facile trovare la soluzione accettabile di t

Noto t, è immediato ricavare la lunghezza apparente d’, fotografata:

d’ = A’B = v t + d

In modo analogo si può calcolare la contrazione, nel caso in cui la velocità abbia verso contrario.

Come potremmo fare per “fotografare” veramente la contrazione di Lorentz e fare contento Albertino? Basta che il righello passi a grande velocità in direzione perpendicolare alla macchina fotografica. Nell’istante in cui si forma l’angolo di 90°, A e B possono lanciarsi insieme verso M, rendendo felice Albertino (Fig. 6).

Abbiamo visto che il quiz ha destato molto interesse. Alcuni ci sono arrivati prima, altri dopo e altri sono rimasti ancora in sospeso… Questa soluzione ha visto l’aiuto fondamentale di Arturo che ha preparato le animazioni che seguono, che mi sono sembrate le più facili da comprendere, oltre ad aver affrontato la parte analitica. Un grazie a tutti, ma a lui in particolare.

Animazioni

Righello fermo (ovviamente non contratto)

 

Righello già contratto in moto con velocità v (si avvicina a M)

 

Righello già contratto in moto con velocità – v (si allontana da M)

 

 

Non crediate, però, che la storia sia finita qui! Questa è stata la parte più facile, la prossima volta sarà già leggermente più difficile. Leggete quindi con attenzione questa favola molto seria in modo da proseguire con il piede giusto…

A presto!!!

Nota fuori dal coro: visioni apparentemente distorte sono, però, frequentissime anche nel mondo comune. Pensiamo alla visione prospettica: lunghezze più lontane si vedono apparentemente più piccole, così come le rotaie sembrano incontrarsi all’infinito. Un’apparente deformazione dell’oggetto che si fotografa dipende, ancora una volta, dal punto da cui viene fotografato. Se un righello viene spostato in varie direzioni, cambia naturalmente la sua lunghezza apparente. Tutto ciò pur restando nell’ambito della fisica classica. Un cubo fotografato assumerebbe forme inaspettate se non avessimo già nel cervello una certa conoscenza delle sue forme previste. Non per niente, quando l’arte è riuscita a capire le leggi matematiche che permettono di costruire queste deformazioni, è riuscita a rappresentare la realtà visiva delle tre dimensioni su un piano. Masaccio insegna…

 

QUI tutti gli articoli dedicati alle visioni relativistiche