Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante.

Dato che il secondo quiz, insieme all’aggiunta , sono solo un punto di passaggio verso una costruzione più laboriosa e forse meno intuitiva, diamo una risposta abbastanza qualitativa, lasciando i calcoli esatti solo a chi avesse proprio voglia di “toccare con mano”. D’altra parte Arturo ha già indicato la strada da seguire nei commenti (QUI).

Ovviamente, la strategia è sempre lo stessa utilizzata per il righello posto in posizione orizzontale (QUI): tutto si riduce a definire gli istanti in cui i punti del righello devono inviare i loro fotoni affinché essi arrivino sulle macchine fotografiche M₁ e M₂ ai tempi t_o e t₂

Facciamo allora muovere con velocità relativistica il nostro righello. E’ chiaro, ormai, che i punti A ed E, i più lontani da M₁, devono inviare per primi il loro raggio di luce. I fotoni (che ci interessano) partono dagli altri punti del righello non appena la distanza tra i punti e M₁ è perfettamente uguale a quella che manca ai fotoni di A ed E per giungere su M₁. In altre parole, questi sono i fotoni che riescono ad arrivare simultaneamente in M₁ al tempo t₀.  L’ultima a partire è, ovviamente, la luce emessa da C, il punto più vicino a M₁.

La Fig. 1 mostra ciò che succede, ma è molto più esplicativa l’animazione preparata da Arturo, più immediata che non quella, parimente ben fatta, di Paolo.

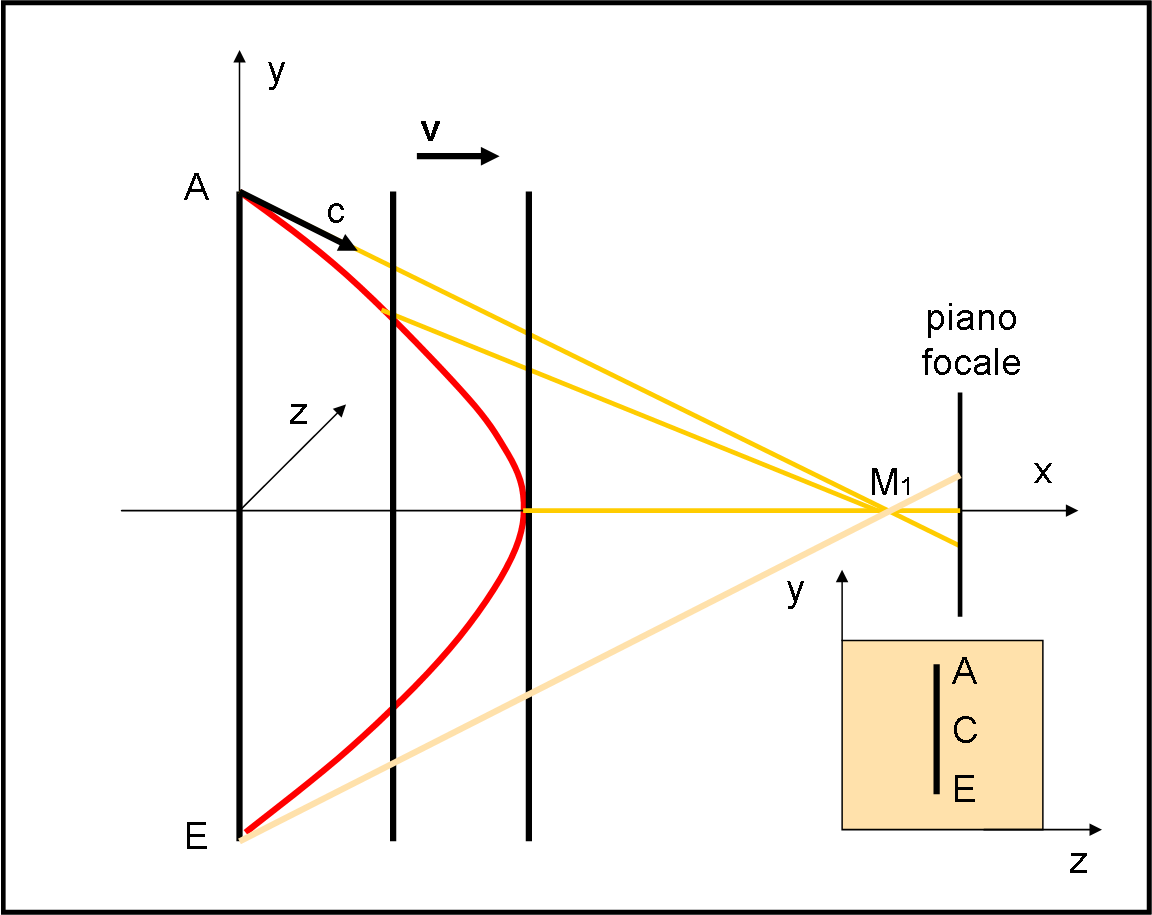
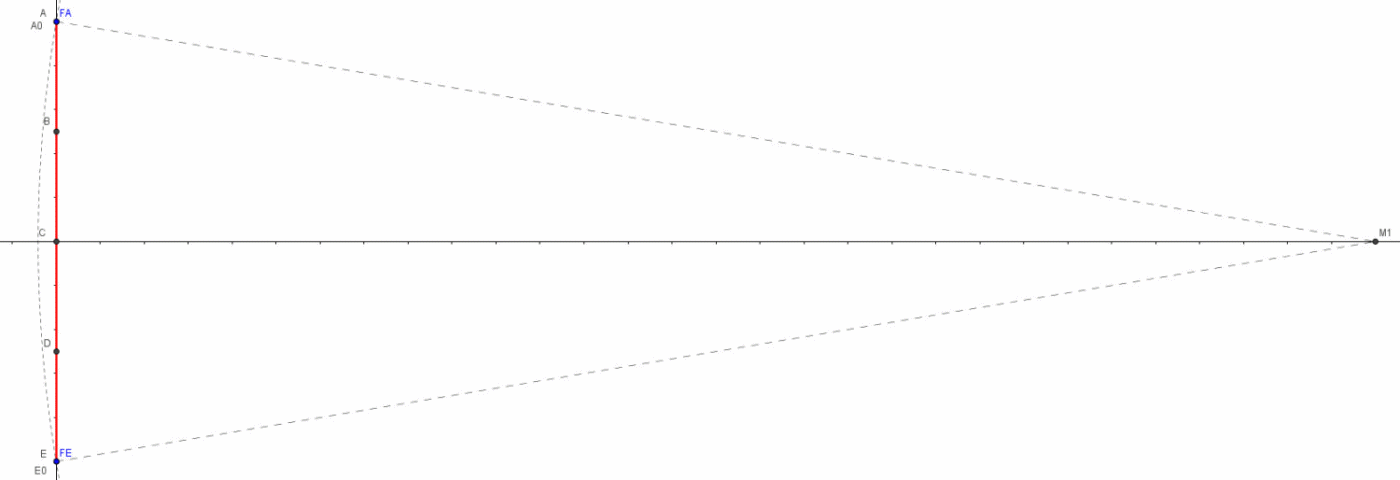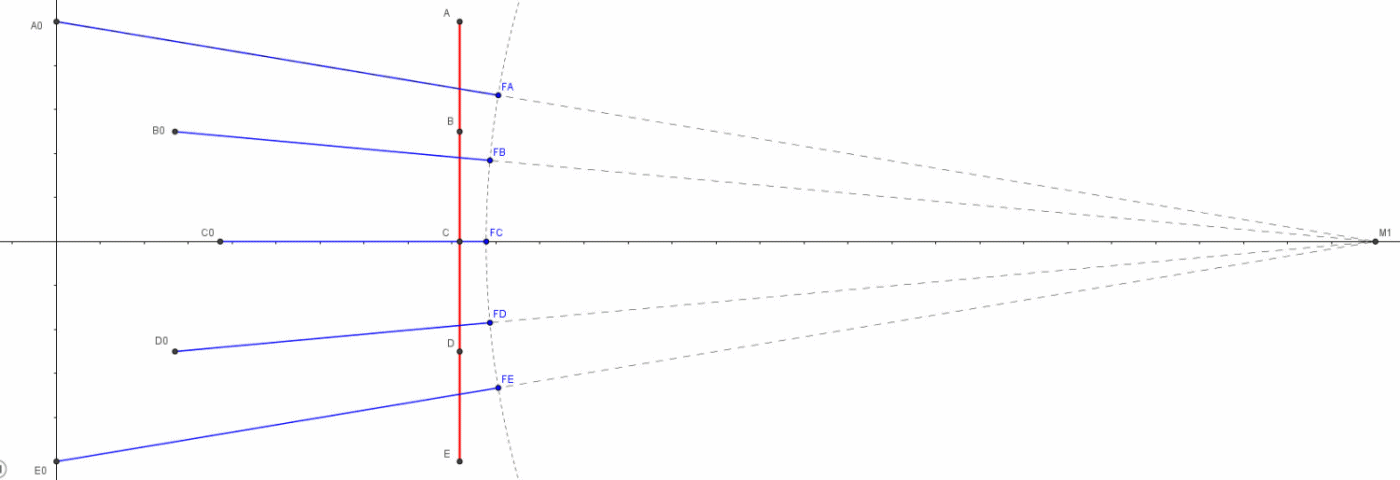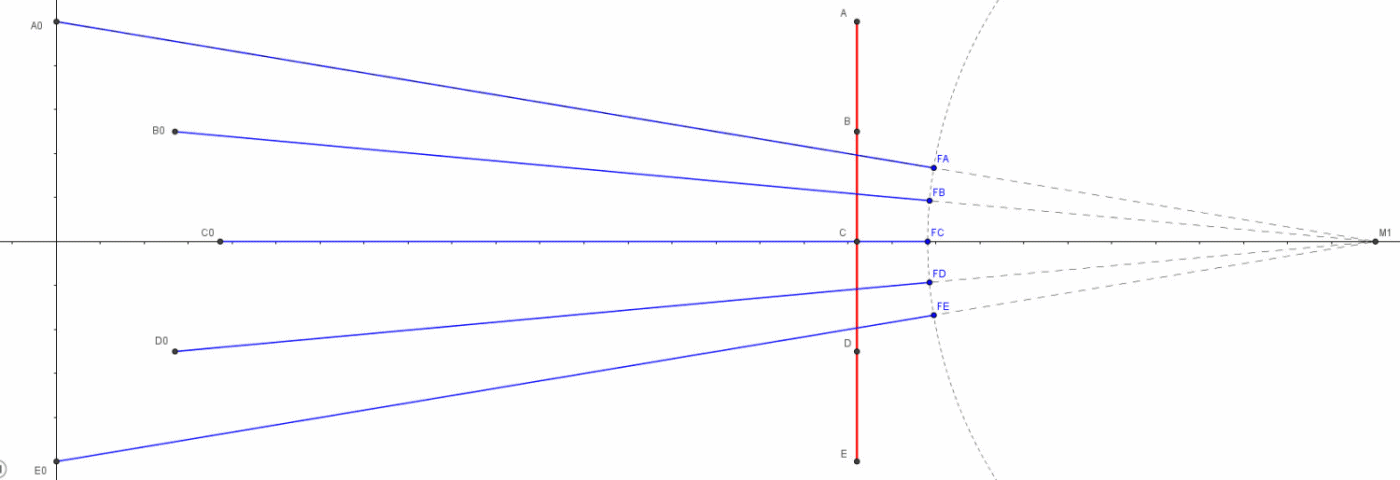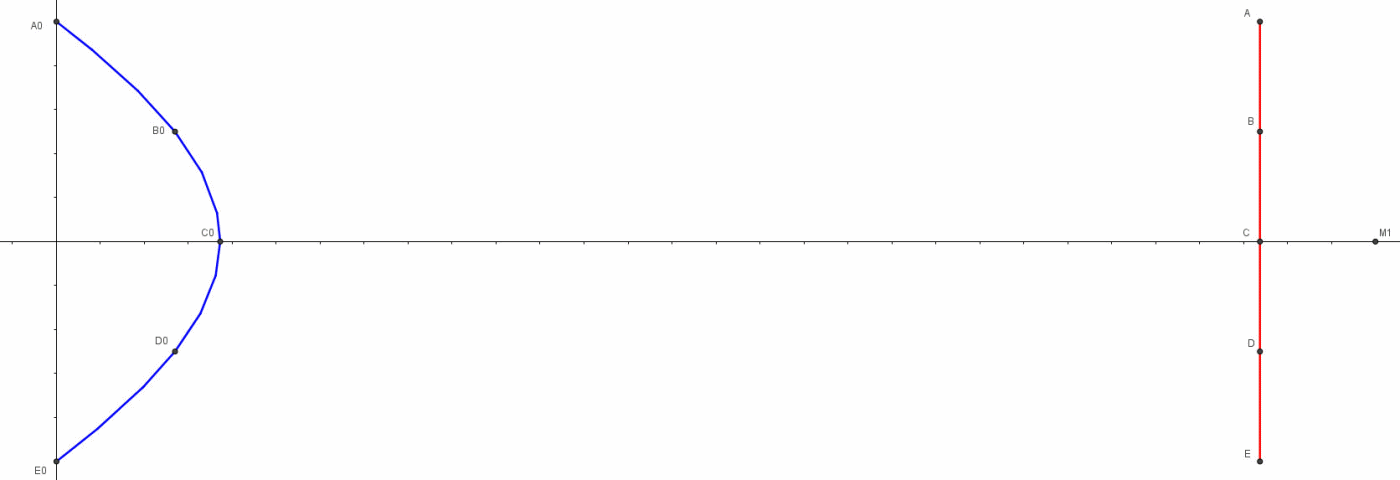
I punti che mandano i loro fotoni in tempi diversi, ma tali da farli arrivare tutti assieme in M₁, descrivono una curva che ha il vertice in C. I punti sono sempre punti dello stesso righello: ciò che cambia è il momento in cui consideriamo l’invio della loro luce e quindi, dato che il righello si avvicina a M₁ con velocità v, essi sono relativi a posizioni sempre diverse del righello. Data la simmetria della figura (l’asse ottico di M₁ passa per il punto di mezzo del righello ed è anche la direzione del moto), si ha sempre una coppia di punti da cui la luce parte simultaneamente, uno sopra e uno sotto all’asse ottico CM₁, come A ed E, B e D, e così via. Solo il punto C rimane singolo e ultimo nell’inviare la luce che ci interessa.

Arturo, nel suo commento, ha dimostrato che questa curva è un’iperbole, di cui un fuoco è M₁. Non sono stati svolti tutti i calcoli, ma, con le indicazioni date, non è difficile arrivare alla conclusione.

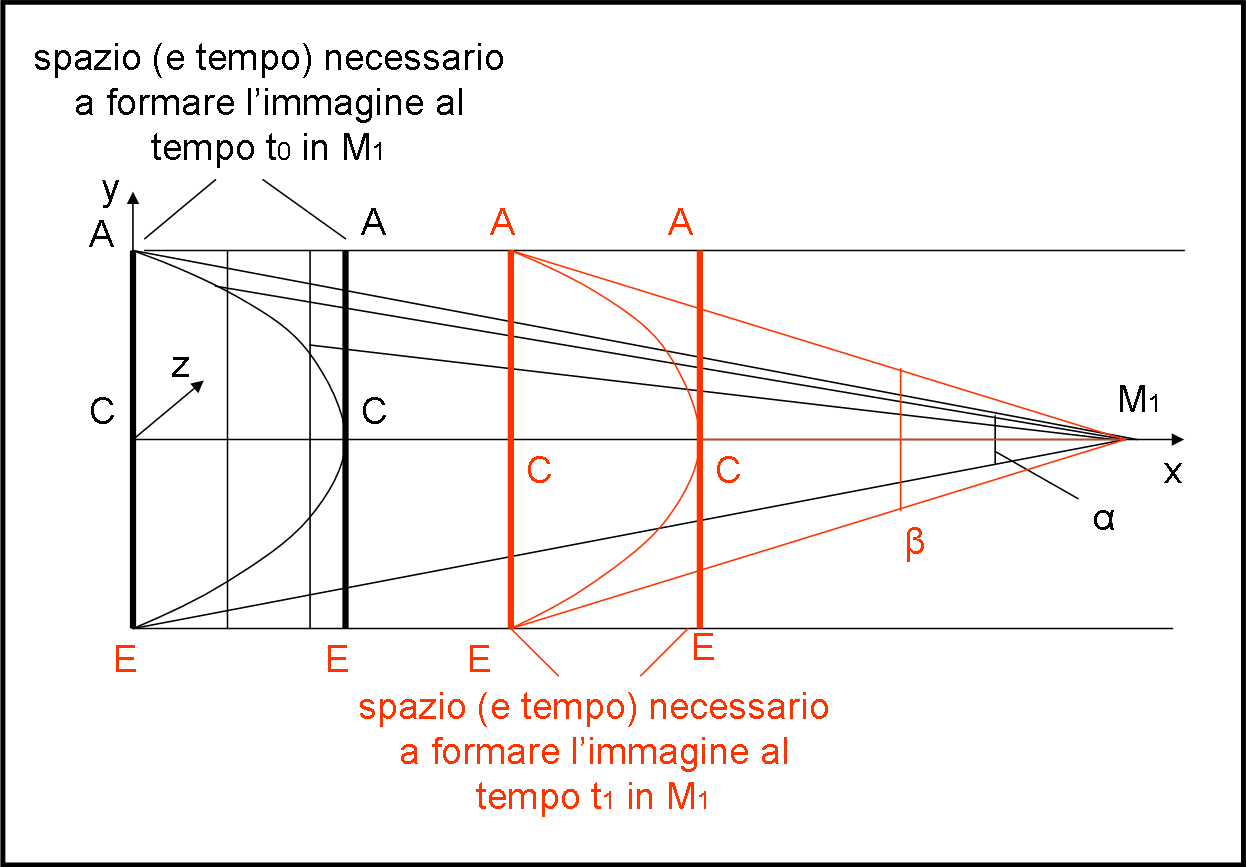
A noi, però, interessa sapere cosa fotografa M₁. Dato che il suo asse ottico è proprio quello della direzione del moto (asse x), a sua volta perpendicolare al righello, ciò che colpisce il piano focale non riesce a evidenziare l’ascissa dei punti di invio. Può solo identificare la loro ordinata, ossia la distanza dal punto centrale C. In poche parole, alla macchina M₁ non interessa assolutamente niente dell’iperbole! Ciò che impressiona la sua pellicola -o quello che preferite- è una linea perfettamente verticale, come disegnato nel riquadro piccolo (piano yz) inserito vicino a M₁. Che il punto centrale abbia inviato la sua luce dopo quella inviata dagli estremi A ed E non può cambiare ciò che giunge tutt’assieme sulla macchina fotografica e che forma l’immagine. La distanza angolare tra A e E resta sempre la stessa ed è, ovviamente, uguale a quella visibile da M₁ all’atto della partenza del righello.

Mettiamo, però, bene in chiaro una cosa: ciò che stiamo raffigurando è relativo a un solo istante t0. Se la macchina fotografica facesse un'altra foto al tempo t₁ > t0, avremmo una diversa lunghezza dell’immagine del righello, dato che esso si è avvicinato, come mostra la Fig. 2 (aumenta la dimensione angolare).

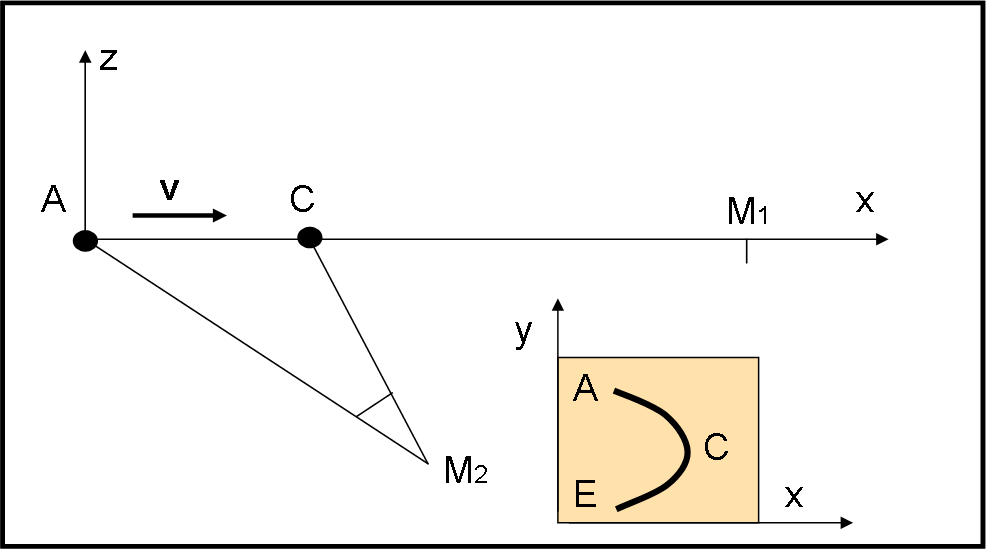
Veniamo brevemente a M₂. Vediamo la situazione dall’alto (Fig. 3), ossia lungo l’asse y. Il righello è un punto che indichiamo con A. In quel momento parte il suo fotone che giunge in M₂ insieme a quello che parte da C in un tempo e in una posizione diversa. Ne segue che nella foto (piano xy) si vede l’iperbole prima descritta. La sua forma dipende molto dalla posizione di M₂, ma su questo punto ci torneremo più avanti.

Digeriamo bene questa parte e prepariamoci a qualcosa di un po’ più complicato e di più “concreto”.

I quiz e l'appendice si trovano QUI, QUI e QUI.

QUI tutti gli articoli dedicati alle visioni relativistiche