Categorie: Relatività
Tags: fotografia quiz relatività ristretta velocità della luce visioni relativistiche
Scritto da: Vincenzo Zappalà
Commenti:6
QUIZ didattico: fotografiamo un righello. 2 ***
Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante.
Come vi avevo già detto, il quiz sul righello e la relativa soluzione erano solo il primo passo verso un’avventura relativistica estremamente stimolante. Ho inserito un asterisco in più solo perché dobbiamo fronteggiare una figura a tre dimensioni… ma chi ha capito la prima parte non avrà problemi a risolvere anche questa seconda parte. La possiamo considerare di “preparazione” a qualcosa di più articolato, dove farà il suo ingresso anche la prospettiva… Per qualche giorno (4-5) sarò in vacanza SENZA PC, per cui divertitevi a fare figure, calcoli (sempre che ne abbiate voglia… ma non è necessario più di tanto) e … animazioni.
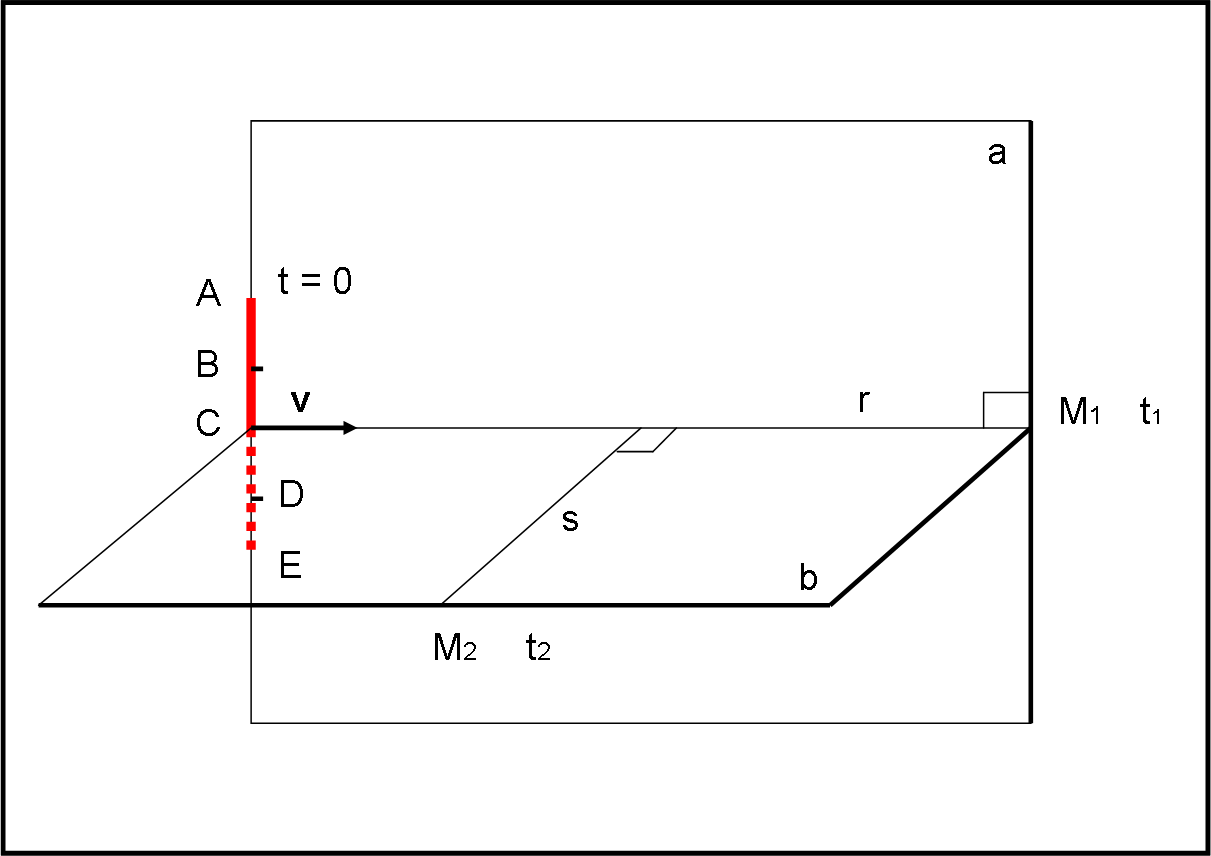
Il righello è sempre lo stesso dell’altra volta e lo possiamo considerare di spessore “nullo” (in poche parole non subisce contrazioni relativistiche). Questa volta utilizziamo due macchine fotografiche che lo fotografino interamente a un certo istante t (può essere anche diverso tra la macchina M1 (t1) e la M2 (t2)). Il righello AE sta nel piano a e inizia a muoversi a velocità costante relativistica verso M1. Il righello è posto perpendicolarmente alla direzione CM1 ed è AC = CE. I punti B e D sono punti medi tra A e C e tra C ed E, rispettivamente (possono essere utili per le varie costruzioni e potete anche usarne di più…). La macchina fotografica M2 è situata nel piano b perpendicolare al piano a. La configurazione è ben visibile e comprensibile nella figura che segue. Il righello si muove a partire dalla posizione disegnata, al tempo t = 0, con velocità costante v. Le due macchine fotografiche hanno un grandangolo e le rette r e s sono i loro assi ottici.
Disegnate le immagini che appaiono nelle due fotografie e (ovviamente) come si creano in funzione del tempo.
Buon divertimento…
QUI un'appendice
QUI la soluzione
QUI il terzo quiz di questa serie
QUI tutti gli articoli dedicati alle visioni relativistiche
6 commenti
Per ora ho affrontato il righello inquadrato da M1. Applicando gli stessi concetti del primo quiz, mi viene fuori codesta animazione. Lo strumento utilizzato per realizzarla è sempre geogebra, partendo dalle equazioni di tutte le entità geometriche che vedete nell'animazione (punti, rette, circonferenze...). A tali equazioni arrivo ragionando sulla geometria del problema specifico, così come si è arrivati nel primo quiz.
Sempre per il discorso che l'immagine in M1 si forma quando arrivano insieme i fotoni provenienti dai 5 punti considerati del righello, e poiché essi non posso partire contemporaneamente per arrivare insieme in M1, per via della velocità relativistica del righello, ottengo che l'immagine del righello che si forma in M1 è "bombata" nella direzione del moto del righello. Però, trattandosi in questo caso di un righello che si muove verso M1 e lungo l'asse ottico di M1 , mi chiedo come potrà essere effettivamente osservata tale "bombatura" da M1. Credo comunque che , almeno da M1, l'effetto sia questo. Se al posto del righello, avessi un piano perpendicolare all'asse ottico e che si avvicina relativisticamente ad M1, lo vedrei bombato , cioè le parti del piano più vicine all'asse ottico sembrerebbero più vicine all'osservatore, rispetto a quelle più distanti dall'asse ottico.
Mumble, mumble
, per provare a vedere cosa inquadrano le due macchine fotografiche, ho realizzato due simulazioni.
Nella prima si utilizza la macchina fotografica che ritrae il righello mentre questo si muove verso l'obiettivo.
In fin dei conti la macchina vede il righello come da fermo (da quella posizione non può accorgersi che il centro del righello si trova "più avanti" rispetto ai lati).
La seconda animazione mostra cosa vede l'altra macchina fotografica, sia quando il righello è in avvicinamento, sia quando è in allontanamento.
Per ragioni grafiche ho mostrato solo il percorso dei fotoni provenienti dalla metà superiore del righello (tanto nella parte sotto accade la stessa cosa, dato che le due parti sono speculari
).
Questa volta il righello appare come i due lati di un triangolo isoscele
, più “allungato” quando si avvicina rispetto a quando si allontana dalla macchina fotografica.
Paolo
Con riferimento alla macchina fotografica M2, con ragionamento analogo a quello da me seguito per M1, direi che l'immagine del righello visto da M2 , nella fase di avvicinamento sia curvata con la convessità nel verso del moto, mentre nella fase di allontanamento sia curvata con convessità opposta.
In questo caso l'animazione basata sulla geometria/fisica del problema implementata in geogebra è resa più complicata dal fatto che siamo nello spazio tridimensionale. Ci vuole più tempo per farla
Ecco l'animazione dalla camera M2, fase di avvicinamento.
La curvatura del righello come visto da M2 è tanto maggiore quanto più vicina è M2 al piano a.
aggiungo un "rallenty" della fase iniziale del movimento del righello verso destra, in cui si vede la partenza dei fotoni FA, FB, FC, FD, FE dai 5 punti significativi A, B, C, D, E del righello ad istanti di tempo tali che tutti e 5 arrivino contemporaneamente alla camera M2. Gli istanti di tempo indicati sono relativi al caso in cui c=1, v=0,9, l (lunghezza righello)=1, xM2=2, yM2=5.
Fornisco di seguito le equazioni di secondo grado da cui si ricavano i valori di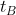
e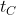 
rispettivamente, essendo 
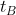l'istante di tempo in corrispondenza del quale parte da B il fotone FB che andrà ad incontrarsi insieme agli altri in M2, e 
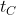l'istante di tempo in corrispondenza del quale parte da C il fotone FC che andrà ad incontrarsi insieme agli altri in M2.
Alle suddette equazioni si giunge con semplici considerazioni geometriche (traiettoria seguita da FB e FC) e tenendo conto che i fotoni si muovono con velocità c mentre il righello si muove con velocità v.