Categorie: Relatività
Tags: fotografia quiz righello verticale velocità della luce visioni relativistiche
Scritto da: Vincenzo Zappalà
Commenti:4
QUIZ didattico: fotografiamo un righello. 2 (BIS) ***
Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante.
Avendo visto le animazioni proposte e la definizione dei punti di partenza della luce, direi che potremmo aggiungere una breve appendice a quanto fatto finora (questo il quiz)
In poche parole, che tipo di curva è quella che caratterizza i vari punti di partenza della luce dalla sbarra in modo che arrivi a un tempo prefissato nelle macchine fotografiche? C'interessa un'equazione in x e y, scelti convenientemente (magari solo nel caso di M1). Inoltre cosa vediamo esattamente nella foto di M1 e M2 (ricordiamo che l'immagine si forma su un piano perpendicolare agli assi ottici).
Dato che la faccenda si complicherà ancora, potremmo anche limitarci a una visione qualitativa senza eseguire calcoli analitici troppo complicati...
QUI la soluzione
QUI tutti gli articoli dedicati alle visioni relativistiche
4 commenti
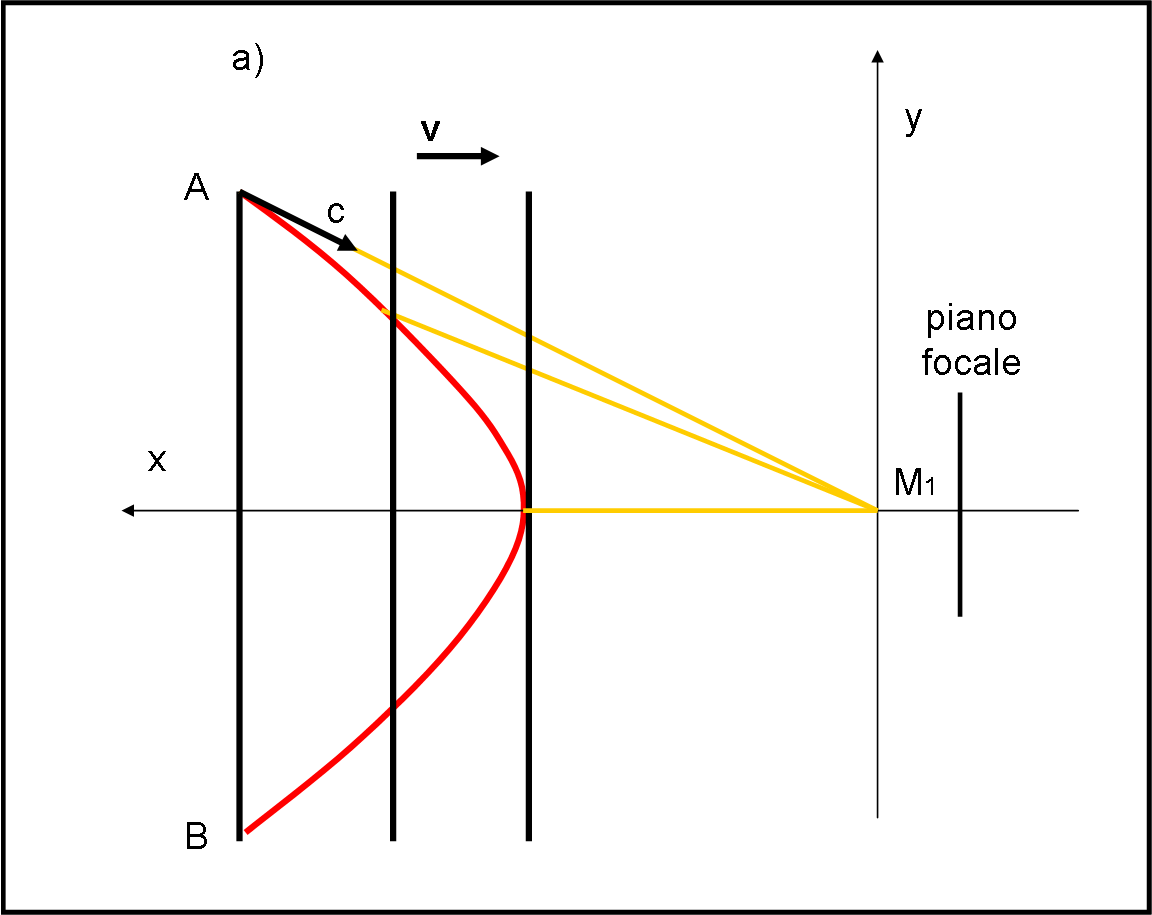
La curva è un'iperbole. L'immagine del righello ottenuta somigliava molto ad un ramo di iperbole, così, per verificarlo, ho fatto il seguente ragionamento.
Ho posto l'origine degli assi O come in figura, cioè coincidente con la posizione di C all'istante iniziale t=0.
Se per caso M1 fosse uno dei due fuochi di un'iperbole ed F1 l'altro, per definizione di iperbole dovrei avere, per ciascun suo punto, la costanza della differenza tra la distanza del punto da M1 e la distanza del punto da F1. Cioè, per esempio, considerando i punti A0 e C0 della curva:
A0M1 - A0F1 = C0M1-C0F1 (1)
AoM1 e CoM1 sono noti:
indico con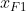
l'ascissa del fuoco F1 dell'eventuale iperbole e ricavo l'espressione di A0F1 e CoF1:
sostituisco tutto nella (1), smanetto un po' con i calcoli e alla fine ricavo l'espressione di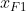
Per la scelta dell'origine, inoltre, l'equazione dell'eventuale iperbole deve essere del tipo
essendo x=xc l'equazione dell'asse dell'iperbole , posto quindi a metà strada tra i due fuochi (o tra i due vertici). Per calcolare xc, mi determino prima la lunghezza del segmento CoP:
quindi
a questo punto , sapendo che rispetto l'asse di equazione x=xc, il fuoco F1 ha ascissa uguale a -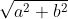
(mentre rispetto all'origine scelta ha ascissa xF1) e il vertice C0 ha ascissa uguale a -a (mentre rispetto all'origine scelta ha ascissa pari a 
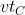) , posso scrivere le due equazioni:
da cui alla fine mi ricavo a e b
Sostituisco le (3), (4) e (5) nella (2) ottenendo l'equazione della eventuale iperbole.
A questo punto sostituisco nell'equazione trovata le coordinate dei punti A0, B0, C0, D0, E0 e mi accorgo che esse soddisfano tutte tale equazione. Cioè che tutti i punti appartengono all'iperbole. Quindi la curva cercata è proprio un'iperbole, di cui uno dei fuochi coincide con la macchina fotografica M1.
per vedere ingrandita l'immagine del precedente commento fare click qui
Scusa Arturo...
quando fai la differenza tra CoM1 e CoF1 non dovrebbe sparire vtC ? Forse si potrebbe semplificare qualcosa...
Ben tornato, caro Enzo
Salvo mie sviste, dovrebbe essere:
E il risultato della suddetta differenza è identico a CoP, come ci si aspetterebbe per ovvie considerazioni geometriche.