Il Paradosso di Borel, parte seconda

27/10/17

Il Paradosso di Borel, parte seconda

Categorie: Matematica Teoria degli insiemi Tags: Scritto da: Umberto Cibien Commenti:1

Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

Blog di Umberto Cibien

 

Facciamo un breve riassunto di quanto visto  la volta scorsa (Paradosso di Borel-parte prima). Per prima cosa abbiamo parlato dei fondamenti essenziali del calcolo delle probabilità, ovvero :

La definizione di probabilità

Cioè la probabilità come rapporto tra casi favorevoli e casi possibili

Probabilità di eventi complementari

Nel caso di un semplice esperimento in cui i casi sono solo due, successo e insuccesso, se p è la probabilità di successo, 1-p è la probabilità di insuccesso

Eventi certi ed eventi  impossibili

Un evento è certo se la sua probabilità è  uno, impossibile se la probabilità è zero

La probabilità di eventi indipendenti

Abbiamo visto che la probabilità di eventi indipendenti è semplicemente il prodotto delle probabilità dei due eventi.

Supponiamo adesso di ripetere un esperimento che abbia solo due esiti; successo o insuccesso.Qual'è la probabilità che in n prove non si verifichi nemmeno un successo ?. Tale probabilità, come abbiamo visto , è  (1-p)^{n}, ovvero che si verifichino n insuccessi consecutivi.

Questo per n prove. Ma è possibile che non esca mai, qualsiasi sia n?
Ripetiamo indefinitamente l'esperimento. Questo equivale a far tendere n all'infinito.  Poiché il limite per n tendente a infinito di (1-p)^{n} è zero,
lim_{n \to +\infty}(1-p)^{n}=0
(essendo q=(1-p) un numero compreso fra zero e uno), la probabilità di non aver almeno un successo se si ripete l'esperimento indefinitamente è zero. Quindi l'evento "almeno un successo" è un evento certo.
E qui salta fuori il paradosso di Borel:
"Può una scimmia battendo a caso delle lettere su una tastiera comporre un poema come la Divina Commedia?"
Ci siamo limitati al problema (semplificato dal punto di vista solo numerico) che ne scriva solo il titolo:
Pensiamo solo alle lettere senza spazi che formano la parola "DIVINACOMMEDIA", che sono 14,  e ad una tastiera semplificata di soli 30 tasti. Per ogni singola lettera abbiamo un probabilità p=1/30 che venga battuta la  lettera giusta, ossia quella che ci aspettiamo(la probabilità  che venga invece battuta un altra lettera, è 29/30). La scimmia batte quindi a caso sulla tastiera: che  probabilità abbiamo che esca  "DIVINACOMMEDIA" ? sono eventi consecutivi di uno schema Bernulliano,  la probabilità di avere 14 successi consecutivi è (\frac{1}{30})^{14}. Questo è un numero molto piccolo (2,03 \cdot10^{-21}).
Sappiamo, da quanto abbiamo visto sopra, che la probabilità che non si verifichi nemmeno un successo ripetendo  per  n prove l'esperimento è data da (1-p)^{n}.
Nel nostro caso dunque tale probabilità è  (1-\frac{1}{30^{14}})^{n} . Sappiamo già che il limite per n tendente a infinito della probabilità  che non si verifichi nemmeno un successo è zero:
lim_{n \to +\infty}(1-\frac{1}{30^{14}})^{n}=0. Quindi, certamente, avremo almeno un successo.
"Soluzione" del paradosso.
La soluzione del paradosso, è che il tempo per scrivere a caso un poema, chè è proporzionale al numero di tentativi, è un numero molto grande, maggiore addirittura dell'età dell'universo.
Vediamo il calcolo nel caso  di 14 lettere; la probabilità che non si verifichi mai un successo è data da:
(1-p)^{n}
ovvero (1-\frac{1}{30^{14}})^{n};
sappiamo invece che la probabilità che  si verifichi almeno un successo è data da(evento complementare):
 1-(1-p)^{n}
nel nostro caso:
1-(1-\frac{1}{30^{14}})^{n}
Limitiamoci a calcolare quando la probabilità  che si verifichi almeno un successo sia superiore al 90%, ovvero 0.9:
1-(1-\frac{1}{30^{14}})^{n}>0.9
cioè:
-(1-\frac{1}{30^{14}})^{n}>-0.1
se cambio i segni cambia il verso della diseguaglianza:
 (1-\frac{1}{30^{14}})^{n}<0.1
questa disequazione esponenziale si risolve applicando i logaritmi:
ricordando che 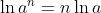\ln a^{n}=n \ln a:
n \ln (1-\frac{1}{30^{14}})< \ln(0.1)
se divido adesso per \ln (1-\frac{1}{30^{14}}), essendo  \ln (1-\frac{1}{30^{14}})< 0   devo cambiare il segno della diseguaglianza:
n>\frac{ln(0.1)}{\ln (1-\frac{1}{30^{14}})}\simeq1101319311964046810181,9939807662=\cong 1.1 \cdot 10 ^{32}; supponiamo pure che la scimmia batti un tasto al secondo \cong 1.1 \cdot 10 ^{21} diventano secondi, mentre sappiamo che l'età dell' universo non supera 10^{18} secondi.
Chiaramente , se consideriamo l'intero poema, il valore di n  sarà di gran lunga maggiore.
Osserviamo un'altra cosa importante: se come valori di probabilità ci avviciniamo  maggiormente ad 1, essendo:
n>\frac{ln(1-p)}{\ln (1-\frac{1}{30^{14}})} (dove nel nostro caso p=0.9) il numeratore diventa un numero in valore assoluto sempre più grande, essendo il logaritmo di un numero sempre più piccolo. Se usiamo un valore che si avvicina di più a 1, tipo 0.9999 troveremo un valore sempre più grande, essendo il denominatore un valore costante. Tale valore quando p=1 è infinito (logaritmo di zero diviso un numero finito).
Concludiamo dicendo che l'evento "scrittura della Divina Commedia battendo dei tasti a caso" non è un evento logicamente impossibile, ma il tempo affinché si verifichi con certezza (probabilità 1) è infinito.

 

Articoli correlati

1 commento

  1. Gianni Bolzonella
    27/10/2017 at 23:07

    ESTERO - LE NOTIZIE MAI LETTE IN ITALIA

    È il risultato del progetto di formazione lanciato negli anni '80
    Singapore ha cambiato insegnamento e adesso ha i migliori matematici
    di Giovanni Galli

    Singapore prima nell'insegnamento della matematica. C'è voluto molto tempo per raggiungere questo primato mondiale. E lo si deve al progetto «Matematica Singapore» lanciato negli anni '80. Una équipe specializzata ha impiegato dai 5 ai 7 anni per elaborare un metodo che è stato sperimentato per i successivi 15 anni, corretto, migliorato in base alle risposte dei test sul campo...

     

    Mi permetto di mettere una nota non pertinente all'argomento,ma ho letto un articolo su Italia Oggi,che parlava di un risultato importante risultato pedagogico della scuola di Singapore.

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.