La probabilità che si verifichi un certo evento (un evento può essere l'uscita di un determinato numero alla roulette, oppure al lotto, ecc.) è un numero p dato dal rapporto fra i casi favorevoli e i casi possibili. In formule:

Esempi (tratti da giochi elementari quali il testa o croce e la roulette):

probabilità che esca testa o croce: 1/2;infatti abbiamo due possibilità di uscita, e una  favorevole

probabilità che esca il rosso alla  roulette: 18/37; i numeri rossi sono 18, mentre i rimanente sono 37

probabilità che esca il nero: 18/37;

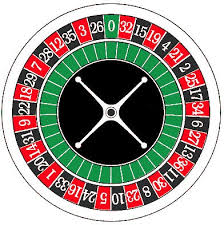
probabilità che esca il rosso o lo zero (quindi che non esca il nero): 19/37;

probabilità che esca il nero o lo zero (quindi che non esca il rosso): 19/37;

probabilità che esca un numero qualsiasi:1/37.

 NOTA: La probabilità è un numero compreso fra zero e uno:

; infatti i casi favorevoli vanno da zero al numero dei casi possibili.

 Se in un gioco,in un esperimento, la probabilità che si verifichi un evento è p e quella che non si verifichi è q , allora  p e q e sono legate dalla formula:

p+q=1

Ciò deriva direttamente dalla definizione di probabilità; siano infatti Nf i casi favorevoli, Nnf i non favorevoli, ;allora :

p=Nf/(Nf+Nnf) ; q=Nnf/(Nf+Nnf);p+q=(Nf+Nnf)/(Nf+Nnf)=1

esempio; la probabilità che esca il rosso è 18/37; quella che non esca 19/37; la loro somma dà 37/37=1

Notiamo dal fatto che p+q=1, se la probabilità di vincere è p, la probabilità di perdere è q=1-p.

 Se un evento ha probabilità 1 allora è un evento certo, mentre se ha probabilità zero è un evento impossibile. Questo discende direttamente dalla definizione di probabilità. Essendo essa il rapporto fra casi favorevoli e casi possibili, se i casi favorevoli sono uguali a quelli possibili, l'evento si verifica certamente. Se in vece tale rapporto è zero, allora i casi favorevoli sono zero, quindi l'evento è impossibile.

Affermiamo che la probabilità di due eventi consecutivi (che non dipendono uno dall'altro) è data dal prodotto delle probabilità. La dimostrazione generica di questa affermazione richiede l'introduzione di concetti quali la probabilità condizionata e di eventi dipendenti e indipendenti; noi la giustificheremo con degli esempi concreti.

Supponiamo di avere delle biglie numerate da 1 a 10 in una scatola. Se estraggo un biglia a caso, la probabilità che sia la numero 1 è 1/10 ( 1 caso favorevole su 10 casi possibili.) Qual'è la probabilità che invece, rimettendo la biglia nella scatola, si estragga ancora la biglia numero 1? Tale probabilità è data da (1/10)*(1/10)=1/100, ovvero è il prodotto delle due probabilità.  Perchè? Anche in questo caso dobbiamo contare i casi favorevoli. E' solo la coppia (1,1) che dà esisto favorevole. E i casi possibili? Sono tutte le coppie possibili, (1,1),(1,2), (1,3)...(1,10)...(2,1),(2,2),..(2,10).......(10,1),.(10,2),...(10,10). che sono 10 x 10=100 quindi la probabilità è ancora 1/100. Complichiamo un po' il ragionamento;Cerchiamo la probabilità che la prima biglia sia 1 e la seconda un numero pari. Siano p,q tali probabilità. Allora p=1/10, q=5/10=1/2, p*q=5/100; infatti i casi favorevoli sono (1,2),(1,4),(1,6),(1,8), (1,10) che sono 5, mentre quelli possibili sono sempre 100; dunque p*q=5/100. Dunque anche se e probabilità sono diverse, la probabilità che accadano i due eventi consecutivi è data dal prodotto delle probabilità.

Supponiamo di voler giocare al rosso/nero; qualsiasi persona tenderebbe a ripetere la giocata sullo stesso colore,in caso di insuccesso.

Abbiamo 19/37 come probabilità che non esca il colore scelto; la probabilità che non esca due volte di fila è in tal caso . E che non esca tre volte?

,quindi , quattro volte , cinque volte  e così via.

Ovvero, se n sono le ripetizioni, tale probabilità è , dove p=18/37.

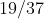n=1	n=2	n=3	n=4	n=5
0.51	0.26	0.13	0.06	0.03

Il gioco che abbiamo illustrato è un caso particolare di un processo che avviene con uno schema detto Bernulliano. Chiamiamo processo di Bernoulli di parametro p la ripetizione indefinita di un esperimento che può dare due esiti alternativi, che indichiamo convenzionalmente coi termini successo e fallimento, con probabilità rispettivamente p e q=1-p. Si suppone che l’esito di una singola prova non sia influenzato dagli esiti delle prove precedenti.Si dice anche che gli eventi sono indipendenti .

 Ciò che attira il giocatore in genere  è il fatto intuitivo che prima o poi debba uscire il colore scelto. Questo è vero, ma non si sa quando. Questo comporta la rovina del giocatore.  Analizziamo meglio la questione. Qual'è la probabilità che in n prove non si verifichi nemmeno un successo ? Riagganciamoci all 'esempio del rosso o nero. Tale probabilità, come abbiamo visto sopra, è  .

Questo per n prove. Ma è possibile che non esca mai, qualsiasi sia n?

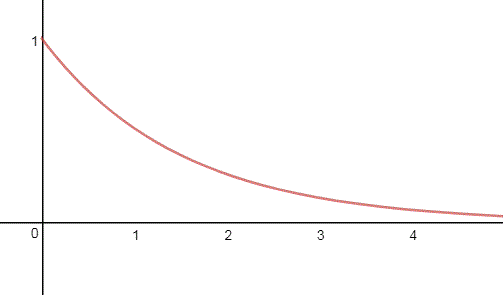
Ripetiamo indefinitamente l'esperimento. Questo equivale a far tendere n all'infinito.  Poiché il limite per n tendente a infinito di  è zero,

(essendo q=(1-p) un numero compreso fra zero e uno), la probabilità di non aver nemmeno un successo è zero. Quindi l'evento successo è un evento certo.

Una conseguenza  di questo fatto,  nota come Paradosso di Borel, è che una scimmia (o un automa) che batte a caso i tasti di una tastiera di computer, ne farà uscire, prima o poi, il testo della Divina Commedia.

Concentriamoci su un esempio più semplice, senza voler scrivere un poema. Pensiamo solo alle lettere senza spazi che formano la parola "DIVINACOMMEDIA", che sono 14,  e ad una tastiera semplificata di soli 30 tasti. Per ogni singola lettera abbiamo un probabilità p=1/30 che venga battuta la  lettera giusta, ossia quella che ci aspettiamo(la probabilità  che venga invece battuta un altra lettera, è 29/30). La scimmia batte quindi a caso volte sulla tastiera: che  probabilità abbiamo che esca  "DIVINACOMMEDIA" ? sono eventi consecutivi di uno schema Bernulliano,  la probabilità di avere 14 successi consecutivi è . Questo è un numero molto piccolo ().

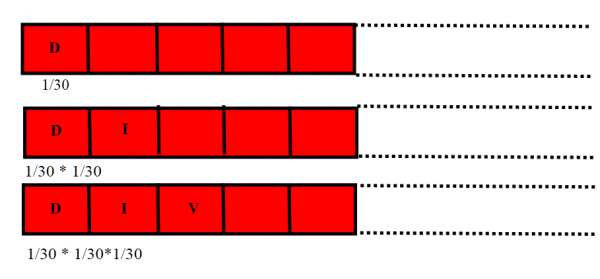
La scimmia continua con  queste ripetizioni per un numero indefinito di volte. Abbiamo quindi uno schema di ripetizione Bernulliano; in questo caso però il successo è un evento composto, di cui conosciamo la probabilità che è  .

Nel nostro caso quindi, p=, mentre q=1-p è la probabilità che non si verifichi, quindi   Sappiamo, da quanto abbiamo visto sopra, che la probabilità che non si verifichi nemmeno un successo ripetendo  per  n prove l'esperimento è data da .

Nel nostro caso dunque tale probabilità è   . Sappiamo già che il limite per n tendente a infinito della probabilità  che non si verifichi nemmeno un successo è zero:

Quindi prima poi dovrà uscire quella combinazione di tasti, formanti la parola "DIVINACOMMEDIA".

Questo discorso vale anche per il poema completo, basta sostituire a 14 il numero di  di lettere che compongono il poema.

Nella seconda parte dell'articolo, vedremo però che questo non è un buon sistema per scrivere poemi.

Il problema non banale sarà quello di calcolare quello che si chiama"tempo medio di attesa" prima che si verifichi un successo. questo ci darà un indicazione di quanto ci  vorrebbe per far scrivere ad una scimmia particolarmente longeva la Divina Commedia.