Categorie: Fisica Matematica
Tags: area del cerchio area del quadrato babilonesi circonferenza egizi pi greco raggio storia antica storia pi greco
Scritto da: Vincenzo Zappalà
Commenti:5
La storia infinita del pi greco. 1 : 24/25 *
Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"
Irrazionale (non è quoziente di due numeri interi), trascendente (non può essere radice di polinomi con coefficienti razionali), non è una costante fisica, ma puramente matematica; tuttavia, sembra che non si riesca descrivere l’Universo senza di essa: entra dappertutto, dal micro al macrocosmo. E’ solo una necessità dell’uomo, che è costretto a inserirla per tentare di spiegare le leggi della Natura, o è invece un qualcosa di profondamente radicato nell’essenza stessa del Cosmo? Forse non lo sapremo mai, ma il pi greco e la sua storia sono un punto chiave di tutta la Scienza e non potevamo fare a meno di dedicargli un articolo approfondito.
14 marzo, nello stile inglese 3/14. 3.14…. è proprio l’inizio di questo fantastico numero, il vero prezzemolo della matematica e della sua applicazione alla Scienza in generale. Questo giorno è stato scelto per celebrarlo e noi ci adattiamo con piacere, anche se leggermente in ritardo (ma lui non ha problemi ad aspettare…).
L’inizio (e la fine?)
Cominciamo a scrivere tre formule che meglio di tante parole possono dimostrare l’importanza del pi greco e darne una visione la più ampia possibile
24/25
ΔxΔp ≥ h/4π
Rμυ - ½ Rgμυ = 8πGTμυ/c4
Il primo è un semplice rapporto che compare in una tavoletta babilonese del 1680 a.C.
Il secondo esprime il Principio di Indeterminazione di Heisenberg, la base di tutta la Meccanica Quantistica, che sancisce l’impossibilità di misurare con estrema accuratezza sia la quantità di moto che la posizione di una qualsiasi particella, lasciando il microcosmo in una generale indeterminazione, con risvolti che potrebbero addirittura legarsi alla nascita stessa dell’Universo.
Il terzo descrive le equazioni della Relatività di Einstein. Esse racchiudono la rappresentazione dell’intero Cosmo e della sua struttura: la materia dice allo spaziotempo come curvarsi, lo spaziotempo dice alla materia come muoversi. Sono proprio loro che trovano le giuste parole per avvicinarsi ai Signori dell’Universo, ai buchi neri, forse ai rifugi finali di tutta la materia.
Sia il possibile inizio che la fine, sia le creature più piccole che le più gigantesche, hanno bisogno del pi greco.
Il primo rapporto ci indica, invece, il probabile inizio della presa di coscienza e conoscenza del fantastico numero da parte dell’uomo. Nel 1936 si trovano, a Susa, vicino a Babilonia, delle tavolette incise dalla cultura babilonese. In una di queste sono riportati i rapporti tra lati e aree e perimetri di vari poligoni. In particolare, vi è una serie di numeri che si riferiscono al lato dell’esagono (uguale al raggio del cerchio circoscritto) e la circonferenza.

Da essi, effettuando la conversione dalla base 60, adottata dai babilonesi, alla decimale si ricava il rapporto tra il perimetro dell’esagono e del cerchio come 24/25, ossia:
24/25 = p/c
Il lato dell’esagono è conosciuto essere uguale al raggio del cerchio, e, quindi:
24/25 = 6r/c
Oggi sappiamo che l’effettiva misura della circonferenza è c = 2πr, per cui è facile ricavare il valore di π deducibile dal rapporto 24/25.
24/25 = 6r /2πr
π = 3 25/24 = 3.125
Probabilmente, questo è il primo valore di π ricavato dall’uomo, anche se la sua vera essenza è ben lontana dall’essere compresa. In realtà, nelle varie misure legate all’agricoltura e all’architettura, quando è necessario passare da linee circolari a linee rette o alle aree in esse contenute, viene utilizzato normalmente il numero 3, che è considerato il rapporto tra perimetro di un cerchio e il suo diametro o, analogamente, tra area del cerchio e area del quadrato di lato il raggio del cerchio. Probabilmente, più che sufficiente per i calcoli necessari alle richieste pratiche.
Forse, ancora più interessante è ciò che si legge nel papiro di Rhind (reperto risalente al 1650 a.C.,circa, ora conservato al British Museum di Londra) su cui lo scriba Ahmes scrive:
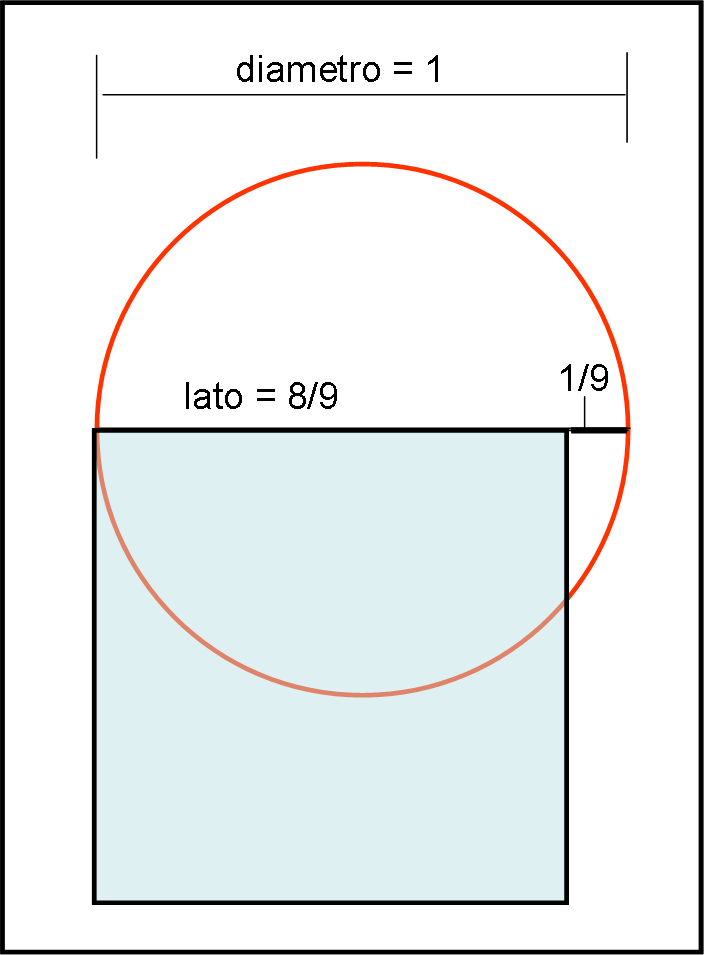
“… Prendi il diametro di un cerchio con diametro unitario, togli 1/9. Ciò che trovi è il lato di un quadrato che ha la stessa area del cerchio…”

Il che vuol dire (Fig. 1):
Diametro = d = 1
Lato quadrato = 1-1/9 = 8/9
Area quadrato = (8/9)2 = area cerchio
Noi sappiamo che area cerchio uguale a π(d/2)2
Area cerchio = π/4 = area quadrato = (8/9)2
π = 4(8/9)2 = 3.16049
Determinazione piuttosto accurata, senza alcun dubbio…
Gli Egizi (forse ancora prima del papiro) avevano ricavato questa affermazione da una esperienza pratica veramente ingegnosa, utilizzando monete tutte uguali tra loro (Fig. 2).
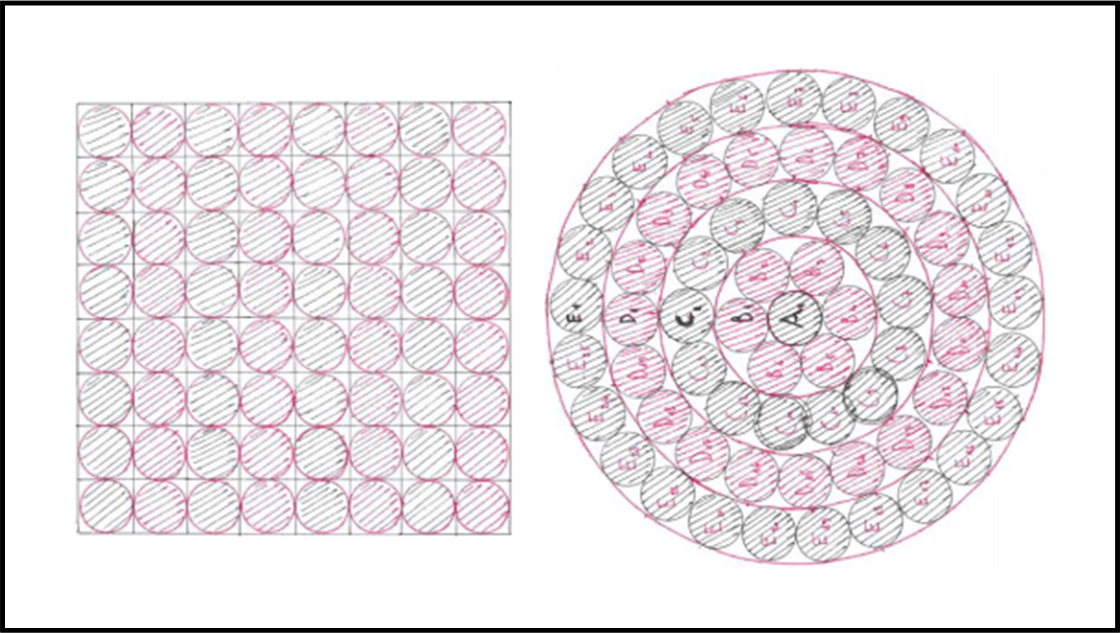
Con 64 monete riuscivano a ricoprire sia un quadrato avente 8 monete per lato sia un cerchio il cui diametro conteneva 9 monete: le due aree erano, quindi, uguali. In particolare, il cerchio era riempito da una moneta centrale attorniata da 4 strati circolari di 6, 13, 19, 25 monete. Modernizzando i calcoli, si ottiene:
r = 9/2 = 4,5
π = Area/r2 = 64/4,52 = 64/20,25 = 3,16049
La piramide di Cheope
Il fascino delle piramidi egizie è indiscutibile. Costruzioni immense eppure di geometria semplicissima. Come potrebbero non nascondere qualche mistero? Segni della presenza di alieni? Allineamenti stellari o planetari incredibilmente complessi e conoscenze astronomiche impensabili per quei tempi? Oppure soltanto una meravigliosa opera dell’ingegno umano, dietro cui si nascondono veri e propri geni dell’architettura? Noi propendiamo per la terza ipotesi e, trattando di un numero fantastico, riteniamo interessante proporre una sua possibile presenza nella realizzazione di una costruzione altrettanto fantastica. Prendiamo il tutto per quello che è e cerchiamo anche di dargli un risvolto molto pratico e poco magico.
La “colpa” di questa dissertazione è di Erodoto, che scrisse chiaramente che la piramide fu realizzata in modo tale che l’area di ogni faccia laterale fosse uguale all’area di un quadrato di lato uguale all’altezza della piramide. Una soluzione che ci porta alla ricerca dell’armonia dell’insieme (necessità pratiche legate strettamente all’estetica), ma che nasconde, ancora una volta, la presenza dell’immancabile pi greco. Divertiamoci un po’…
Il problema è puramente di geometria solida, ma noi –che possiamo perché sappiamo- ci facciamo aiutare dall’algebra. Aggiungeremo, ovviamente, anche un bel teorema di Pitagora (prima o poi descriveremo anche la sua storia altrettanto affascinante).
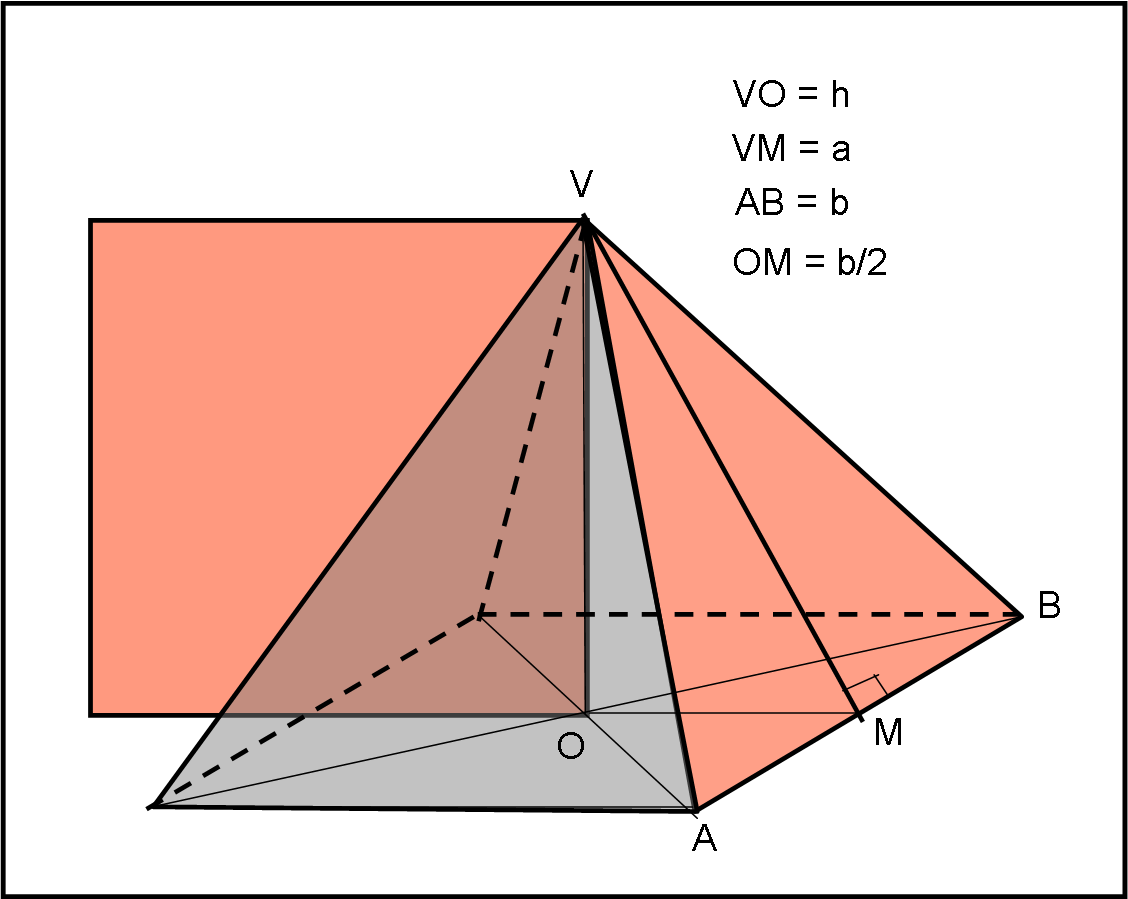
Consideriamo la Fig. 3 , dalla quale possiamo scrivere:
Area quadrato = area triangolo laterale
h2 = b·a/2 …. (1)
h2 + b2/4 = a2
Risolviamo il sistemino, inserendo la prima relazione nella seconda:
b·a/2+ b2/4 = a2
da cui ricaviamo a
a = (b +/- b√5)/4 = (b/4) (1 + √5) (escludendo la soluzione negativa)
Sostituendo nella (1), si ha:
h2 = (b2/8) (1 + √5)
b2/h2 = 8/(1 + √5)
estraendo la radice quadrata
b/h = 2√ (2/(1 + √5)) = 1.5722 ≈ π/2 (1.5708)
Probabilmente è solo un caso, ma…
QUI gli altri articoli dedicati all'infinita storia del pi greco






5 commenti
Ciao Enzo, decisamente interessante come tutti i numeri di questo tipo cioè ad es. radice di due, numero aureo, ecc. Però sulla conclusione "piramidale" quasi ci cascavo, non credo che le cose siano andate a questo modo propendo più per una soluzione pratica che matematico-geometrica. Sicuramente erano in grado di fare questi conti e li avranno fatti ma anche se la precisione della piramide di Cheope (per esempio) viene accreditata di solo una decina di cm di errore tra i lati la pratica probabilmente ha avuto il sopravvento sulla teoria. Mi spiego, ho visto e "toccato" le piramidi della piana di Giza e non solo, stabilire la precisione in dieci cm mi pare una forzatura visto che non esiste un reale spigolo e in ogni caso propendo più per un problema di precisione degli strumenti di allora che non a reali errori di calcoli vari. A mio parere a volte ci si fa prendere la mano e si forza oltre la necessità (di allora). Quel che scrivo è semplicemente frutto di quel che ha smosso l'articolo nella mia testa cioè primo essendo 3,14 un numero onnipresente lo si può far saltar fuori da quasi tutte le figure solide e non, ma qui sarai tu, che sei il matematico ad eventualmente smentirmi. Secondo faccio un esempio di praticità per intendere come ingegnandosi si possa fare una piramide pur essendo a digiuno di tutto di cui sopra: Supponiamo di dover fare 8 fori con centro fori di diametro A su di una flangia di diametro B dove naturalmente B è maggiore di A. Semplicissimo basta avere un compasso e pazienza, punto il centro eseguo una traccia (cerchio) del diametro centro fori, segno un punto sul questo cerchio e poi divido a occhio con il compasso partendo dal punto fino a quando, aggiustando il compasso, non trovo una misura che sta con precisione ragionevole dentro questo cerchio otto volte. In meccanica si chiama tracciatura e quando non si dispone di strumenti è l'unica via, la precisione raggiungibile, senza grande sforzo, è inferiore al decimo di mm (garantisco fino a 1,6 m di diametro tracciato) e non occorre alcuna conoscenza matematica-geometrica teorica. Se si conosce la formula del diametro del cerchio si ha pure una prima approssimazione per puntare il primo giro di "compassate". Quindi anche per una piramide, volendo, con qualche corda a disposizione si può ottenere il risultato.
Cool
caro Frank,
anch'io ho qualche dubbio (lo dico anche) ... tuttavia la determinazione NON deriva da misure fatte, ma da quanto ha detto Erodoto. In altre parole, qualsiasi piramide costruita secondo la sua descrizione darebbe come risultato quel pigreco mezzi. La piramide di Cheope potrebbe benissimo non essere mai stata costruita, ma rimarrebbe la volontà di costruire qualcosa in cui vi siano certi rapporti tra lati e altezze...
Ovviamente, Erodoto non avevo certo misurato la piramide e quindi la sua descrizione geometrica doveva provenire da tradizioni, scritti o disegni di origine egizia.
Una possibile spiegazione potrebbe essere collegata al metodo di misura utilizzato dagli egizi per le distanze sul terreno: un rullo circolare. Distanze misurate sulla base della circonferenza e altezze misurate -magari- mediante "diametri"... insomma un pi greco che nascerebbe dalla differenza del tipo di misurazione... Ma anche questa ipotesi non mi convince molto. Chi è capace di costruire meraviglie come i templi egizi era sicuramente in grado di fare disegni e di scegliere le proporzioni, imponendo poi il loro rispetto finale.
Insomma, Frank... il problema non era certo fare una piramide (per loro era una sciocchezza), ma decidere le sue proporzioni. Anch'io potrei fare una Gioconda, ma sarebbe ben diversa da quella del mio grande amico Leonardo...
Si Enzo, come al solito riesci a sintetizzare al meglio. Ho spostato l'attenzione su Cheope ma il soggetto rimane il 3,14. Forse è lecito scindere in due, "3,14" per la pratica e "pi greco" con la sua irrazionalità per la matematica. Alla fine 3,14 è una necessità pratica facilmente ricavabile con approssimazione più che sufficiente all'uso comune. Tutta un'altra storia le incredibili elucubrazioni dei matematici di allora come Erodoto. Anche ridurre al solo perimetro, come ho fatto, la piramide di Cheope è una forzatura, la piramide è molto di più di quel perimetro. Forse lo stesso si può dire di radice di due, per questo aspetto l'articolo dedicato come hai quasi "promesso" .
Hai notato l'ordine di precisione della tracciatura paragonato ai dieci cm su 230 m della piramide?
PS i critici d'arte potrebbero preferire la tua Gioconda, basta che ti vendi bene.................. Dai provaci.