Categorie: Relatività
Tags: astronavi quiz relatività ristretta tempo trasformazioni di Lorentz velocità
Scritto da: Vincenzo Zappalà
Commenti:42
Quiz relativistico: esplosioni terrestri e solari ** (NEW: con piccolo aiuto)
Ormai le astronavi viaggiano tranquillamente nel Sistema Solare e la direzione Terra-Sole (e viceversa) è una rotta molto seguita. Ogni tanto può capitare di assistere a fenomeni non previsti. I problemi nascono quando si vuole calcolare l'intervallo di tempo tra di essi.
Le velocità raggiunte sono tali che possiamo considerare la Terra e il Sole senza moto relativo tra di loro. In altre parole, essi appartengono a un unico sistema di riferimento. Tra di loro vi è una distanza "fissa" di 8.3 minuti luce. A un certo istante t = 0 sulla Terra esplode un vulcano. Due minuti dopo (tempo terrestre) il Sole ha una violenta esplosione.
La domanda (doppia) è: "Qual è la differenza di tempo tra i due eventi per un osservatore di un'astronave che viaggi con una velocità pari a 0.8 quella della luce lungo la rotta che passa prima dalla Terra e poi dal Sole? Qual è, invece, quella nel caso di un'astronave che viaggi nella direzione opposta con la stessa velocità?"
Attenzione... cerchiamo di ragionare attentamente! Le domande potrebbero avere un seguito, molto istruttivo... La Relatività Ristretta non smette mai di sorprendere!
N.B.: Abbiamo chiesto la differenza di tempo tra due eventi in un sistema di riferimento in moto rispetto a quello Terra-Sole.
PICCOLO AIUTO:
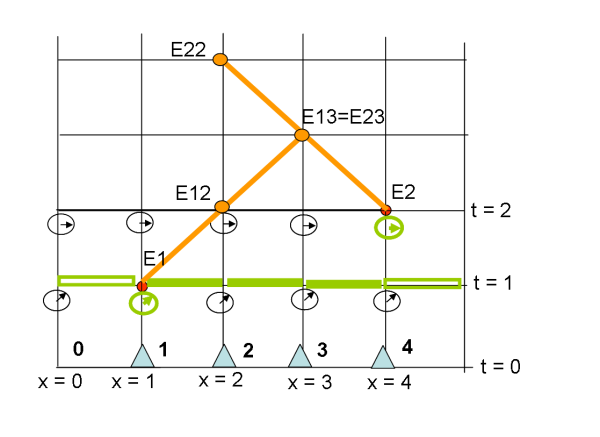
Richiamiamo cosa s'intende per sistema di riferimento e per evento misurato in tale sistema di riferimento. Per preparare il sistema si devono usare righelli unitari e orologi sincronizzati, in modo da ottenere ciò che si vede nella figura che segue.
Immaginiamo che vi siano 4 astronavi (1,2,3,4) che si muovono solo nel tempo, ossia sono ferme spazialmente. All'istante t = 0, tutte le astronavi misurano lo stesso tempo. L'evento E1 (vulcano?) ha la stessa coordinata temporale per tutte le astronavi, mentre varia la sua coordinata spaziale. Stessa cosa capita per l'evento E2 (brillamento?). Tuttavia, per tutte le astronavi la differenza tra il tempo e la distanza spaziale dei due eventi è sempre uguale. Anche facendo muovere le astronavi (nel tempo), le differenze temporali e spaziali tra i due eventi non cambiano. In poche parole, tutte le astronavi concordano sulle differenze tra coordinate di due eventi.
Possiamo adesso considerare un altro tipo di evento: qundo e dove la luce di E1 incontra l'astronave 2. Chiamiamo questo evento E12. Aggiungiamo anche l'evento E22 che indica il luogo e il tempo in cui la luce di E2 incontra l'astronave 2. In altre parole, abbiamo indicato gli eventi relativi alla visione dei due eventi da parte dell'osservatore in 2. Se considerassimo l'astronave 3, i due eventi "visione degli eventi E1 ed E2" coiciderebbero sia spazialmente che temporalmente in E13=E23.
In conclusione: separiamo bene gli eventi tra di loro e cerchiamo di capire bene il sistema di riferimento. Ogni astronave descrive un evento secondo le sue coordinate (considerandosi come origine degli assi), ma le differenze tra coordinate rimangono sempre le stesse. L'origine degli assi è del tutto ininfluente per valutare le differenze temporali e spaziali tra eventi diversi.
Nel problemino sottoposto stiamo parlando di due eventi E1 ed E2 e non di eventi tipo E12 o E23, ecc. L'unica vera differenza è che vogliamo calcolare le coordinate degli eventi così deffiniti in un altro sistema di riferimento inerziale che si muove relativisticamente rispetto al primo. Tutto qui...
Le cose più interessanti potremo vederle e discuterle successivamente...
QUI la soluzione
42 commenti
Nota Bene
Temo che il problema sia stato mal compreso... Nel sistema spaziotemporale Terra-Sole vi è una certa differenza temporale e spaziale tra due eventi. Noi abbiamo chiesto la differenza di tempo tra gli stessi due eventi in un sistema di riferimento in moto rispetto a quello Terra-Sole.
Questo piccolo aiuto è stato anche inserito nel testo del quiz...
PICCOLO AIUTO:
Richiamiamo cosa s'intende per sistema di riferimento e per evento misurato in tale sistema di riferimento. Per preparare il sistema si devono usare righelli unitari e orologi sincronizzati, in modo da ottenere ciò che si vede nella figura che segue.
Immaginiamo che vi siano 4 astronavi (1,2,3,4) che si muovono solo nel tempo, ossia sono ferme spazialmente. All'istante t = 0, tutte le astronavi misurano lo stesso tempo. L'evento E1 (vulcano?) ha la stessa coordinata temporale per tutte le astronavi, mentre varia la sua coordinata spaziale. Stessa cosa capita per l'evento E2 (brillamento?). Tuttavia, per tutte le astronavi la differenza tra il tempo e la distanza spaziale dei due eventi è sempre uguale. Anche facendo muovere le astronavi (nel tempo), le differenze temporali e spaziali tra i due eventi non cambiano. In poche parole, tutte le astronavi concordano sulle differenze tra coordinate di due eventi.
Possiamo adesso considerare un altro tipo di evento: qundo e dove la luce di E1 incontra l'astronave 2. Chiamiamo questo evento E12. Aggiungiamo anche l'evento E22 che indica il luogo e il tempo in cui la luce di E2 incontra l'astronave 2. In altre parole, abbiamo indicato gli eventi relativi alla visione dei due eventi da parte dell'osservatore in 2. Se considerassimo l'astronave 3, i due eventi "visione degli eventi E1 ed E2" coiciderebbero sia spazialmente che temporalmente in E13=E23.
In conclusione: separiamo bene gli eventi tra di loro e cerchiamo di capire bene il sistema di riferimento. Ogni astronave descrive un evento secondo le sue coordinate (considerandosi come origine degli assi), ma le differenze tra coordinate rimangono sempre le stesse. L'origine degli assi è del tutto ininfluente per valutare le differenze temporali e spaziali tra eventi diversi.
Nel problemino sottoposto stiamo parlando di due eventi E1 ed E2 e non di eventi tipo E12 o E23, ecc. L'unica vera differenza è che vogliamo calcolare le coordinate degli eventi così deffiniti in un altro sistema di riferimento inerziale che si muove relativisticamente rispetto al primo. Tutto qui...
Le cose più interessanti potremo vederle e discuterle successivamente...
Visto il silenzio-assenso che circonda questo quiz, arrischio la mia interpretazione....
Innanzi tutto non credo che si voglia discutere sul fatto che si veda prima l'eruzione e poi il brillamento o viceversa, a seconda della posizione o a seconda della direzione del moto. Questo forse non ci interessa.
Quello che si chiede è come si modifica l'intervallo di tempo tra i due eventi visto dalle astronavi.
Ebbene , dato che tra due sistemi in moto relativo, a velocità comparabili a quella della luce, esiste una precisa relazione per quanto riguarda la percezione del tempo, direi che dalle astronavi, che si muovono entrambe alla velocità di 0,8 C , lungo la direttrice terra sole ( una in un senso, l'altra nel senso opposto) l'intervallo di tempo viene percepito dilatato del fattore di Lorentz (gamma) che a quella velocità vale 1,66666.
Gamma = 1/ radq(1-(v/c)^2)
Se sbaglio mi corriggerete...
caro Mau... temevo un poco questo tipo di risposta. Pensaci bene... dilatazione del tempo e contrazione delle lunghezze sono due casi particolari nella trasformazione di coordinate. Nel caso del tempo, vale solo se gli eventi non hanno distanza tra di loro nel sistema in cui sono definiti (t,x). (Per chi è nel sistema a terra non vi è stato spostamento spaziale tra i due eventi, ma solo temporale...). Nel nostro caso non è così. Il fattore gamma compare ma in un ambito più generale. L'importante è seguire passo passo la trasformazione di Lorentz, come fosse una trasformazione di coordinate qualsiasi. Se due eventi capitano nel sistema fermo, essi avranno un delta t per il treno e un delta t per l'ossevatore a terra, ma i due eventi NON hanno, nel caso del quiz, un delta x uguale a zero per il sistema fermo. Basta fare una bella figura minkowskiana e il tutto si vede molto bene... Ricordiamo anche che i due eventi non sono assolutamente collegati causalmente tra di loro e nessuno vuole viaggiare tra uno e l'altro, ma solo determinarne le coordinate.
Per adesso ci interessano gli eventi "esplosione"... gli eventi "vedere le esplosioni" è un problma aggiuntivo, da capire molto bene...
Resto un po' nel confuso, ma se dico di più, risolvo il quiz... Al limite potrei fare una figura "muta" con le linee, ma senza spiegare cosa sono i vari punti e via dicendo... ma aspetto ancora un po'.
In particolare: il problema è decisamente più semplice di quello che può sembrare... è solo un cambiamento di coordinate e basta!
Aggiunta:
guardatevi bene la Fig. 32 de
http://www.infinitoteatrodelcosmo.it/2015/10/01/lo-spaziotempo-di-minkowski-luniverso-in-un-foglio/
e capirete che la dilatazione del tempo è un caso particolare del problema più generale della trasformazione di coordinate di due eventi in due sistemi di riferimento (uno in moto rispetto all'altro).
Caro Enzo, ieri sera ho finalmente avuto il tempo di provare a trovare la soluzione usando il diagramma di Minkowski:
https://postimg.cc/image/hewq3r1p1/
Nella figura che ho realizzato ho disegnato solo gli assi del tempo (t per il sistema terricolo, t’ per l’astronave che dalla Terra va verso il Sole, t’’ per l’astronave che dal Sole va verso la Terra), le linee di simultaneità per le due diverse rotte, corrispondenti agli eventi A (vulcano che esplode sulla Terra) e B (eruzione solare).
Se la figura è corretta questo potrebbe essere un possibile colloquio che confronta i diversi punti di vista:
Terricolo: i nostri strumenti indicano chiaramente che prima il vulcano ha eruttato e dopo 2 minuti c’è stata l’eruzione solare.
Comandante dell’astronave in rotta dalla Terra verso il Sole: i nostri strumenti (sistema di riferimento t’) indicano chiaramente che prima c’è stata un’eruzione solare e dopo circa 7,8 minuti è esploso un vulcano sulla Terra.
Comandante dell’astronave in rotta dal Sole verso la Terra: i nostri strumenti (sistema riferimento t’’) indicano chiaramente che prima è eruttato il vulcano sulla Terra e dopo circa 14,34 minuti c’è stata un esplosione sul Sole.
I tempi sono stati ricavati graficamente, per cui sono approssimativi…
Volendo, però, si possono ricavare in maniera più accurata attraverso le trasformazioni di Lorentz (ovvero con una trasformazione di coordinate):
t’ = (t - βX) γ
t’b = (tb - βXb) γ = (2 – (0,8 x 8,3)) 1,666 = -7,73 minuti
t’a = (ta - βXa) γ = (0 – (0,8 x 0)) 1,666 = 0 minuti
∆T’ = (t’b – t’a) = (-7,73 - 0) = - 7,73 minuti (il segno meno indica solo che gli eventi A e B vengono visti “invertiti” rispetto al terricolo)
Nel caso dell’astronave in rotta dal Sole verso la Terra, cambia il segno della velocità (β)
t’’b = (tb + βXb) γ = (2 + (0,8 x 8,3)) 1,666 = 14,39 minuti
t’’a = (ta + βXa) γ = (0 + (0,8 x 0)) 1,666 = 0 minuti
∆T’’ = 0 – 14,39 = 14,39 minuti
Spero sia corretto!
Paolo
Se bisogna usare le trasformazioni di Lorentz così come sono state trattate, c'è solo un modo per usarle, ovvero di dove posizionare al tempo t=o l'astronave e il suo sistema di riferimento. E il tutto si riduce a a un calcolo semplice, come dici. Pur intuendo che è vero, ma è proprio banale il fatto che la differenza dei tempi non dipenda dalla posizione relativa dell'astronave? Nell'aiuto inserito tu lo hai dimostrato per le astronavi ferme assieme agli eventi, ma nell'altro coso mi sembra un po' differente la questione.Per quanto riguarda la seconda parte, quello della visione, ho provato a fare i calcoli, ma la differenza di tempi non mi viene indipendente dalla posizione dell'astronave.Penso di aver sbagliato qualcosa.
caro Umberto,
io, per adesso, ho chiesto solo la differenza degli eventi E1 ed E2, non della loro visione. Per gli eventi richiesti non cambia mai la differenza di tempo. Quindi puoi calcolarla tranquillamente nei due casi (v e -v)... la soluzione è, come dici tu, veramente banale ma fa capire bene una situazione più generale che si potrà discutere...
caro Paolino,
non dico ancora niente sulla risposta numerica. Posso solo dire che la figura potrebbe essere resa un po' più didattica disegnando proprio i due sistemi di riferimento e qualche linea in più... (tu mi capisci...). Almeno io la penso così, dato che una figura più completa darebbe il via a una serie di chiarimenti e piccole discussioni. Oltretutto, i conti espressi nella figura non sono chiarissimi... (pensiamo a chi deve leggerli e capirli...).
ho parlato di visione solo perché l avevi citata in uno degli ultimi commenti. Del resto ritengo questo problema più interessante del primo.
ovviamente sì, caro Umberto... ma è per partire dalle cose più facili per cercare di non ... spaventare. Ma sembra che non sia così facile per molti... Lorentz è proprio la base!
Nel riferimento dell'astronave i diagrammi dovrebbero essere questi per l'astronave che va dalla sole alla terra, il primo, e dalla terra al sole, il secondo.
Qui ho fatto passare l'astronave sopra la terra nel momento dell'eruzione. Se passase in qualche altro istante i diagrammi sarebbero solo traslati senza modifiche delle differenze dei tempi. Le distanze indicate sono quelle calcolate per i diagrammi di Minkowski.
Per il calcolo numerico può convenire utilizzare direttamente le trasformazioni di Lorentz.
Per ottenere l'intervallo di tempo in un riferimento, noti intervalli di tempo e distanze in un altro, la trasformazione è:
in minuscolo intervalli tra gli eventi nel riferimento terra-sole ed in maiuscolo quelli nel riferimento astronave. La velocità v è quella dell'astronave nel sistema di riferimento terra-sole. Nel sistema di riferimento dell'astronave la velocità della terra e del sole sono -v.
I valori a destra sono noti
In quest'ultimo caso, per il riferimento dell'astronave avviene prima E2 e poi E1.
Volendolo calcolare a partire dai diagrammi si vede che contribuiscono a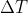
2 intervalli, quello corrispondente all'intervallo spaziale di lunghezza 8,3 (distanza terra-sole in unità relativistiche nel riferimento terra-sole) e quello corrispondente all'intervallo temporale 2 (intervallo temporale tra i due eventi nel riferimento terra-sole). Per il modo con il quale vengono calcolate le distanze temporali nei diagrammi di Minkowski i due contributi dovrebbero essere:
Caro Enzo, per la figura fino a stasera non ho a disposizione photoshop, per fare qualche aggiunta o modifica.
Posso, invece, provare a spiegare i calcoli riportati in figura.
Innanzitutto, alla velocità di 0,8 c corrisponde un fattore di 1/γ = 0,6
L’intervallo di tempo che separa i due eventi (a e B) secondo il sistema di riferimento terricolo, è pari a 2 minuti.
Per trovare l’intervallo di tempo ∆t’ che separa i due eventi (A e B) secondo il sistema di riferimento blu (astronave in rotta dalla Terra al Sole), ho tracciato la linea di simultaneità (linea parallela all’asse x’, non indicato in figura) che congiunge l’evento B (eruzione solare) all’asse t’.
Per l’evento A, non ce n’è stato bisogno, dato che questo interseca direttamente l’asse t’.
Invece di indicare le unità di misura sull’asse t’, ho usato la relazione che lega il tempo t’ al tempo terricolo t, ossia:
∆t’ = ∆t/γ
L’evento A, secondo il sistema terricolo, interseca l’asse t’ al tempo ta =0.
La linea di simultaneità dell’astronave blu, unisce l’evento B all’asse t’, al tempo t1 = -13.
Ciò significa che il punto di intersezione con l’asse t’, indica quando avviene l’evento B secondo l’astronave blu.
Tale evento per il sistema di riferimento t’, avviene prima dell’evento A, ossia per l’astronave in rotta dalla Terra al Sole, prima c’è l’eruzione solare, poi c’è l’eruzione del vulcano.
L’intervallo di tempo ∆t’ trascorso tra i due eventi è quello che separa sull’asse t’ l’evento A, dall’intersezione tra la linea di simultaneità blu che parte dall’evento B e l’asse t’.
Invece di indicare le unità di misura sull’asse t’, mi sono limitato ad eseguire una semplice trasformazione, usando i tempi t corrispondenti ad A (ta) e all’intersezione tra B e l’asse t’ (t1), visti dal sistema terricolo (le linee tratteggiate nere sono le linee di simultaneità per il sistema terricolo).
Quindi:
∆t’ = ∆t/γ = (ta – t1)/γ = (0 – (-13)) 1/γ = 13 x 0,6 = 7,8 minuti
Se avessi tracciato le unità di misura sull’asse t’, avrei ottenuto lo stesso risultato, d’altronde quando t =1 la linea di simultaneità terricola interseca l’asse t’ quando questo segna 1/γ, ossia t’= 0,6 (dilatazione del tempo).
Per trovare l’intervallo di tempo ∆t’’ che separa i due eventi secondo il sistema di riferimento rosso (astronave in rotta dal Sole verso la Terra), ho tracciato le linee di simultaneità (linee parallele all’asse x’’, non indicato in figura) che congiungono rispettivamente l’evento A (eruzione vulcano) e l’evento B (eruzione solare) all’asse t’’.
Anche in questo caso per trovare l’intervallo di tempo ∆t’’ che separa le due intersezioni tra le linee di simultaneità degli eventi A e B e l’asse t’’, ho usato i tempi corrispettivi segnati dal sistema terricolo, con le sue linee di simultaneità.
All’intersezione tra l’evento A e l’asse t’’, corrisponde il tempo terricolo t2 = -18,4 (vedi linea tratteggiata nera di simultaneità terricola), mentre all’intersezione tra l’evento B e l’asse t’’ corrisponde il tempo terricolo t3 = 5,5 (vedi linea tratteggiata nera di simultaneità terricola).
Quindi, come prima:
∆t’’ = ∆t/γ = (t3 – t2)/γ = (5,5 – (-18,4)) 1/γ = 23,9 x 0,6 = 14,34 minuti
Spero, che così il metodo usato sia più chiaro.
Paolo
se consideriamo la terra come origine x del sistema terra sole e lo scoppio al tempo t=0 dello stesso sistema e se prendiamo l astronave che passa per la terra al tempo t=0 basta applicare la formula per i tempi ottenendo -464 che mi sembra in secondi lo stesso tempo di Paolo. Chiaramente se un tempo é zero per trovare la differenza basta trovare il secondo.Nel sistema terra il secondo ha coordinate 120,498. Nel sistema astronave t'=5/3 (120-0.8*498)=-464.Analogamente si procede bel secondo caso.
Il testo del quiz afferma che la direzione terra sole e viceversa è una rotta molto seguita. Mi sarei aspettato una figura un po' diversa, con ambedue le astronavi collocate all'interno dello spazio tra terra e sole, l'una diretta verso la terra e l'altra diretta verso il sole.
Ponendo l'astronave che si allontana dal sole all'esterno di questo spazio, il suo movimento risulta comunque in allontanamento anche dalla la terra. Questo particolare non dovrebbe modificare i calcoli visti fino ad ora, in relazione a come la dislocazione nel tempo e nello spazio determina , per i sistemi in movimento, una diversa valutazione dell'intervallo di tempo tra i due eventi del tipo E1 ed E2 ma credo faccia differenza quando si andrà a valutare gli altri eventi, di tipo E12 o E23, nella seconda parte.
caro Mau,
come dici tu, nel caso degli eventi E1 ed E2 non ha alcuna importanza se la rotta passa proprio dalla Terra e dal Sole... conta solo che sia parallela a questa direzione e sia percorsa a pari velocità. Non ha neanche importanza quando capitano i due eventi: l'importante è la loro differenza temporale. Ovviamente, ciò non vale più se consideriamo gli eventi "esplosioni viste dall'astronave".
Limitiamoci, però, al primo caso e facciamo delle belle figure per far capire bene la situazione e per dimostrare l'indipendenza dei delta x e delta t rispetto alla reale traiettoria e al tempo del primo evento. Sono cose banali, ma è il modo migliore per fare amicizia con la RR e con la rappressentazione di Minkowski.
Comunque, nella figura che sto mettendo a punto considero proprio la traiettoria Terra-Sole e Sole-Terra...
Ma se sulla terra il brillamento viene visto due minuti dopo l'eruzione questo non sta a significare che è avvenuto 6,3 minuti prima dell'eruzione? Ossia il brillamento è avvenuto ad un certo istante e la sua immagine ha raggiunto la terra 8,3 minuti dopo, quando l'eruzione si era già verificata da 2 minuti.
Insomma il "delta t" nel sistema terra-sole vale 6,3 minuti oppure vale 2 minuti (considerando l'istante in cui la luce del brillamento arriva alla terra)?
Aggiungo questo diagramma per provare a descrivere meglio l’ultima parte della mia risposta precedente.
Il diagramma è nel riferimento dell’astronave.
X e T (maiuscole) sono le coordinate nel riferimento dell’astronave, mentre x e t (minuscole) sono le coordinate nel riferimento Terra-Sole.
Dal diagramma si vede che è la somma di due addendi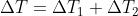
Terra e Sole si muovano a velocità u rispetto all’astronave. Questa velocità è uguale e contraria alla velocità v dell’astronave nel riferimento Terra-Sole (u=-v). Le linee blu e gialla rappresentano il movimento della Terra e del Sole in questo riferimento. Lungo queste linee vale questa relazione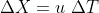
E1 rappresenta l’evento eruzione. Si trova sulla terra, quindi sulla linea blu. L’ho messo nell’origine del rifermento astronave (X=0,T=0). Scelta comoda che non influisce sul risultato di questo quiz come ha spiegato Enzo.
E1s rappresenta l’evento localizzato sul Sole e simultaneo ad E1 nel riferimento Terra_Sole. Si trova sulla linea grigia che passa per E1.
La linea grigia è la retta che congiunge gli eventi simultanei ad E1 nel sistema di riferimento Terra-Sole. Su questa linea vale la relazione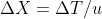
La distanza relativistica totale tra E1s ed E1 coincide con la distanza spaziale dei due eventi nel sistema di riferimento Terra-Sole (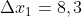
minuti in unità relativistiche). La distanza temporale non contribuisce alla distanza totale poiché è nulla in questo riferimento essendo gli eventi simultanei.
La distanza relativistica totale tra E1s ed E1 nel sistema di riferimento astronave è^2-\Delta&space;T_1^2}=\Delta&space;T_1&space;\frac{\sqrt{1-u^2}}{u})
Ho utilizzato la relazione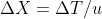
che esiste tra i punti della linea grigia.
Cambiando sistema di riferimento cambiano intervalli temporali e distanze spaziali tra gli eventi, ma la distanza relativistica non varia. Quindi deve valere questa relazione
dalla quale è possibile ricavare
che una delle due parti di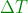
.
E2 rappresenta l’evento esplosione sul Sole. La distanza relativistica totale tra E2 ed E1s coincide con la distanza temporale tra i due eventi nel sistema di riferimento Terra-Sole (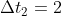
minuti ). La loro distanza spaziale è nulla essendo entrambi collocati sul Sole.
La distanza relativistica totale tra E2 ed E1s nel sistema di riferimento astronave è
Ho usato la relazione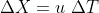
che esiste tra i punti della linea gialla.
Per il fatto che la distanza relativistica totale non varia cambiando sistema di riferimento deve valere questa relazione
dalla quale è possibile ricavare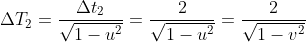
Quindi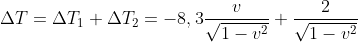
che è l'espressione finale della risposta precedente e coincide con una delle trasformazioni di Lorentz.
Ho provato a disegnare due astronavi con origini diverse,O',O'' e il sistema terra-sole di origine O , nel primo caso.il segmento giallo e quello verde che rappresentano la differenza di tempo dei due eventi E1 E2 nei rispettivi sistemi sono effettivamente uguali. Quello che si forma delimitato dai pallini rossi è infatti un parallelogramma. Quindi è indipendente dalla posizione iniziale dell'astronave.
caro Fabry,
mi sa che sei stato troppo "simmetrico" nel riportare i due eventi... Almeno io capisco così la tua figura...
pensaci un po' sopra...
caro Fabry,
io mi riferivo alla tua prima figura...
caro Mau,
gli eventi brillamento ed eruzione vengono misuraati dagli orologi sincronizzati del sistema Terra Sole, I due minuti sono la differenza di tempo tra questi due eventi misurati da qualsiasi orologio del sistema, Altra cosa è misurare il tempo di un altro evento, ossia il raggiungimento sulla Terra della luce del brillamento. Noi vogliamo solo considerare i primi due eventi che avvenìgono a distanza di due minuti nel SISTEMA Terra-Sole e sapere come questo intervallo di tempo si trasforma nel SISTEMA di un astronave che viaggia tra la Terra e il Sole o viceversa...
Posssiamo fare il calcolo banalissimo e poi disegnare con Minkowski considerando uno o l'altro sistema come fermo.
caro Umberto,
come avevo già detto, qualsiasi traslazione dell'astronave o del sistema Terra-Sole non può comportare differenze, dato che i due sistemi rappresentano uno spaziotempo in cui tutti gli orologi sono sincronizzati tra loro. Ciò che cambia è la differenza temporale passando da un sistema all' altro (relatività della simultaneità...).
PER TUTTI:
I metodi usati e gli scopi dei vari commenti sono abbastanza discordanti. Rimaniamo al quiz senza cercare di estrapolare oltre.
Il quiz si risolve in modo immediato da un punto di vista matematico, applicando la trasformazione di Lorentz. Sembrerebbe più difficile la rappresentazione grafica nel piano spaziotemporale di Minkowski, dove dobbiamo trovare lo stesso risultato, sia considerando come sistema fermo quello Terra-Sole, sia quello dell'astronave.
Invito perciò tutti a ragionare con calma, magari utilizzando una qualsiasi velocità e non proprio 0.8 che stringe troppo la figura (intanto il calcolo è già stato fatto abbastanza in sintonia).
Una figura alla volta, però... per non creare confusione:
Non preoccupiamoci di cambiare origine degli assi nei due casi: abbiamo già visto che questo non influenza assolutamente le differenze di coordinate!
3. sistema fisso quello dell'astronave che viaggia tra Terra e Sole e sistema in movimento quello Terra - Sole. L'astronave parte dalla Terra e arriva al Sole.
4. sistema fisso quello dell'astronave che viaggia tra Sole e Terra e sistema in movimento quello Terra-Sole. L'astronave parte dal Sole arriva sulla Terra. (in pratica si cambia di segno alla velocità)
Anche in questo caso si può cambiare tranquillamente l'origine deggli assi da un caso all'altro, il risultato non cambia.
NON preoccupatevi di usare la velocità giusta, basta mostrare come restino fisse le coordinate degi eventi nel sistema Terra-Sole (gli eventi sono collegati a loro) invertendo la velocità (ossia la direzione), mentre cambino quelle del sistema astronave (gli eventi non sono collegati a loro).
Solo dopo aver digerito bene queste quattro figure, si può iniziare a discutere degli eventi "visione dell'eruzione e del brillamento" e ragionare un attimo sulla peculiarità del concetto dilatazione e/o contrazione, che vanno intesi come casi particolari della trasformazione.
INVITO anche altri lettori a non farsi suggestionare da quanto scritto nei commenti (il succo è sempre lo stesso, ma le motivazioni diverse) e seguire quanto richiesto in questo commento: basta eseguire i vari passaggi con la dovuta calma e attenzione, disegnando tutte le linee anche abbondando... in modo da essere perfettamenti chiari. Non cerchiamo di sintetizzare rischiando confusione...
FORZA, è un eserizio facile e che vi aiuta ad avere maggiori certezze sulla RR di base.
penso che trattandosi di un quiz ognuno abbia il diritto di affrontarlo come meglio crede. Per quanto mi riguarda richiedendo un valore numerico é stato in qualche modo risolto.Se ci saranno altre domande cercherò di dare il mio contributo.Per ora torno ai miei impegni sugli spazi topologici.
Giusto per verificare cosa intendi chiedere , questa è la prima figura con astronave in movimento dalla terra (origine) al sole, con velocità di circa 0,5c... Et= evento sulla terra Es = evento sul sole
Il delta t , di 2 minuti nel sistema fisso ( x t) terra sole, si traduce nel delta t' (da origine a P) nel sistema di coordinate mobili ( x' t' ) della astronave (linee rosse).
Questo in termini puramente grafici. Se coincide con la tua richiesta proseguo a ragionare sugli altri tre casi.
Questo sarebbe il secondo caso....
Ora l'origine è nel sole al momento del brillamento (prima era nella terra al momento dell'eruzione)
L'astronave si muove dal sole alla terra con velocità 0,5 c
Et rappresenta come prima l'evento sulla terra e Es quello sul sole.
Il delta t , di 2 minuti nel sistema fisso ( x t) terra sole, si traduce nel delta t" (da origine a P) nel sistema di coordinate mobili ( x", t") della astronave (linee blu).
caro Mau, il mio dubbio nei tuoi riguardi era questa frase scritta nel primo commento:
l'intervallo di tempo viene percepito dilatato del fattore di Lorentz
pensavo che facessi solo delta t' = gamma (delta t)
caro Umberto,
nessuno obbliga nessuno! Io ho solo consigliato di descrivere il problema in modo chiaro per tutti, senza limitarsi a una risposta frammentaria che non dice nemmeno quali formule o grafici siano stati usati. Il lettore medio vorrebbe una spiegazione adeguata... non tutti sono maghi!
Finora si è sempre cercato di rispondere ai quiz, cercando di spiegare la logica che gli sta dietro...
E nessuno è obbligato a risolvere il quiz... ovviamente. Pensavo di fare cosa utile nel richiamare concetti base della RR..., ma chi è già ben preparato può benissimo farne a meno. Che sia facile lo dimostrano i due asterischi ...
In effetti quel commento era piuttosto sintetico e non entrava nei dettagli.... sarebbe stato meglio metterci anche qualche conto con i dati disponibili, come hanno fatto gli altri amici.
Caro Mau... un ulteriore consiglio per non creare confusione nei meno esperti. Sarebbe bene non prendere l'origine nel primo evento, ma scaglionarli durante il volo Terra-Sole e viceversa. Certe conferme si vedrebbero meglio... Magari prendere proprio la Terra all'andata e il Sole al ritorno (tanto non cambia niente nel traslare un sistema, dovendo lavorare con differenze).
grazie Mau... era proprio quello che intendevo dire con il mio consiglio scritto nei commenti. Anche le figure di Paolo e Fabrizio non aiutano molto nel fare chiarezza al problema rappresentato graficamente.
Questo è un caso che matematicamente è di immediata soluzione, ma che graficamente aiuta ad andare un po' avanti. Ecco perchè ci tengo ad avere figure semplici e chiare... (come le tue ultime, a parte la scelta dell'origine... ma quello è solo un mio pensiero del tutto personale).
nessuna polemica..ma penso solo che nessuno meglio di te può spiegare bene ai lettori la soluzione.
Cato Umberto anche io penso che sia così, ma la speranza e la ricompensa di un maestro è di insegnare fino al punto di venire superato dai suoi allievi.
Non siamo ancora a questo punto, (per ora) quindi insistiamo...
cari amici,
mi avete più volte dimostrato che quando volete superate facilmente il ... maestro!!! E ne sono ultra contento (vedi cono e geodetiche... e non parliamo dei topi...).
Caro Fabrizio,
ho capito perchè la tua prima figura dà un risultato "strano". Tu hai ribaltato la figura in alto rispetto all'asse x. il che vuol dire che hai invertito il tempo, ma lasciato la velocità uguale... e uindi le due figure coincidono... (infatti hai anche invertito i due eventi in modo da lasciarli simmetrici rispetto all'asse x). Ti torna?
E l'altro quesito accennato, quello della visione dell'eruzione e del brillamento ( E13=E23) verrà formulato qui o in un altro quiz?
Penso sia molto interessante.
I diagrammi per i primi due casi indicati da Enzo dovrebbero essere questi.
Il riferimento è quello della Terra-Sole. Il loro moto relativo è considerato trascurabile rispetto a quello dell'astronave.
Astronave in viaggio dalla Terra al Sole
Astronave in viaggio dal Sole alla Terra
L’intervallo di tempo che cerchiamo è quello indicato con
Il procedimento per calcolarlo è lo stesso in entrambe i casi
E1: evento eruzione sulla Terra
E2: evento brillamento solare
E1A: evento simultaneo ad E1 nel riferimento astronave
E2A: evento simultaneo ad E2 nel riferimento astronave
Nota: E1A ed E2A si trovano sull’asse T (o parallelo all’asse T) del riferimento dell’astronave poiché in quel riferimento hanno la stessa coordinata spaziale. Quindi la loro distanza è proprio il tempo trascorso tra i due eventi nel riferimento dell'astronave.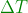
prima trovo le coordinate dei suoi due punti estremi, E1A ed E2A, e poi calcolo la distanza tra questi punti.
Per calcolare
Il riferimento che uso ha l'istante t=0 coincidente con l'evento E1 e l'origine del riferimento è nella posizione dell'astronave a t=0.
Questa scelta non modifica il risultato e riduce la complessità delle formule.
Coordinate di E1A![\mathbf{[x_1_a,t_1_a]}](http://latex.codecogs.com/gif.latex?\mathbf{[x_1_a,t_1_a]})
=t_1_a&space;\\&space;x_1_a=v\;&space;t_1_a&space;\end{matrix}\right.)
=t_1_a\\&space;(v^2\;&space;t_1_a-t_1_a)=v\;x_t\\&space;\end{align*})
E1A si trova alla intersezione della linea d’universo dell’astronave con la retta degli eventi simultanei ad E1 nel riferimento dell’astronave. Quindi le coordinate devono soddisfare contemporaneamente le due equazioni di queste rette.
Sostituendo nella prima la seconda ottengo
Coordinate di E2A![\mathbf{[x_2_a,t_2_a]}](http://latex.codecogs.com/gif.latex?\mathbf{[x_2_a,t_2_a]})
=(t_2_a-t_2)\\&space;x_2_a=v\;&space;t_2_a\\&space;\end{matrix}\right)
E2A si trova alla intersezione della linea d’universo dell’astronave con la retta degli eventi simultanei ad E2 nel riferimento dell’astronave. Quindi le coordinate devono soddisfare contemporaneamente le due equazioni di queste rette.
Procedo come sopra
Calcolo di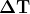
^2-(x_2_a-x_1_a)^2&space;\\&space;\Delta&space;T^2&=\left&space;(\frac{-(v\;x_s-t_2)+v\;x_t}{1-v^2}&space;\right&space;)^2-&space;v^2\;\left&space;(\frac{-(v\;x_s-t_2)+v\;x_t}{1-v^2}\right&space;)^2\\&space;\Delta&space;T^2&=\frac{1-v^2}{(1-v^2)^2}\left&space;(t_2-v\:(x_s-x_t)&space;\right&space;)^2\\&space;\Delta&space;T^2&=\frac{(t_2-v\:d_t_s)^2}{1-v^2}\\&space;\end{align*})
}{\sqrt{1-v^2}}})
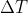dipende dalla differenza 
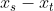che è la distanza 
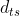tra Terra e Sole. Questo indica che non dipende da come posizioniamo il riferimento.
}{\sqrt{1-0,8^2}}=-7,733\:&space;\textup{min})
\:8,3)}{\sqrt{1-0,8^2}}=14,4\:&space;\textup{min})
Ore che ho trovato le coordinate dei due punti estremi posso calcolare la loro distanza (relativistica)
Nota:
Sostituendo i valori dati nel quiz nel caso di astronave che va dalla Terra al Sole
nel caso di astronave che va dal Sole alla Terra
Caro Fabry,
adesso andiamo molto meglio...
Per Umberto:
direi di concludere il quiz a questo livello, descrivendo i vari passaggi in modo estremamente didattico. Dopo, possiamo anche proseguire e quindi se vuoi cominciare a pensare al secondo passo fai pure: lo riprenderemo, ma non so ancora se come quiz o come trattazione nuovamente molto didattica. In qualche modo, si fa un bel ripasso della trasformazione di Lorentz e dell'iperbole di calibrazione...
La posizione della visione dei due eventi E1 ed E2 dall'astronave mi sembra venga abbastanza direttamente nei due diagrammi nel mio commento sopra. Basta utilizzare le rette a +/-45° della propagazione della luce invece di quelle di simultaneità, poi il procedimento è lo stesso.
Caro Enzo ho realizzato due figure e qualche breve ragionamento.
La prima confronta l'astronave in rotta dalla Terra al Sole, con il sistema terricolo.
https://postimg.cc/image/z8pz44kol/
Per confrontare l'intervallo di tempo che separa i due eventi (A eruzione vulcano e B eruzione solare) misurato dal sistema terricolo con quello dell'astronave, è possibile usare le trasformazioni di Lorentz.
Per i terricoli:
ta= 0; tb= 2; xa = 0; xb = 8,3 e la velocità dell'astronave rispetto alla luce è 0,8c.
Innanzitutto si ricava il valore del fattore di Lorentz:
γ = 1/√(1- v²/c²) = 1/√(1- 0,8²) = 1/0,6
Dopodiché si ricava l'intervallo di tempo Δt’, che separa i due eventi secondo l'astronave, ricordando che:
t’ = (t – vx) γ
t'a = (ta – vxa) γ e t'b = (tb – vxb) γ
Δt’ = (t'b – t'a) = (tb – vxb) γ - (ta – vxa) γ
Δt’ = (tb – vxb -ta + vxa) γ
Δt’ = ((tb -ta) -v (xb - xa)) γ
Δt’ = ((2 -0) -0,8 (8,3 - 0))/0,6
Δt’ = (2 -(0,8 (8,3))/0,6 =
Δt’ = (2 -(0,8 (8,3))/0,6 = -7,73 minuti
Il valore trovato è negativo solo perchè per l'astronave l'evento B avviene prima dell'evento A, per cui tb è minore di ta.
Infine usando le trasformazioni di Lorentz si ricava anche l'intervallo di spazio Δx’, ricordando che
x’ = (x – vt) γ
x'a = (xa – vta) γ e x'b = (xb – vtb) γ
Δx’ = (x'b – x'a) = (xb – vtb) γ - (xa – vta)
Δx’ = (xb – vtb - xa + vta) γ
Δx’ = ((xb- xa) – v (tb -ta)) γ
Δx’ = ((8,3- 0) – 0,8 (2 -0)) /0,6
Δx’= (8,3 – (0,8 (2)) /0,6 = 11,16 minuti luce
Giusto per conferma nella figura intervallo di tempo Δt’ corrisponde a un intervallo misurato sull'asse del tempo t di -12,88 minuti.
Visto dal sistema di riferimento del terricolo, il tempo dell'astronave appare dilatato, ossia:
Δt’ = Δt 1/γ = -12,88 x 0,6 = -7,73
Inoltre per il sistema del terricolo, anche lo spazio dell'astronave appare contratto (x =18,6) :
Δx’ = Δx 1/γ = 18,6 x 0,6 = 11,16 minuti luce.
I risultati ovviamente coincidono!
Infine ciò che non cambia per i due sistemi di riferimento è la distanza spaziotemporale tra i due eventi, ossia:
T² – X² = T'²- X'²
T² – X² = 2² – 8,3² = -64,89
Il segno meno indica che i due eventi non possono essere connessi tra loro, ossia uno non può essere la causa dell'altro (d'altronde in 2 minuti la luce, ossia l'informazione, non può certo percorrere 8,3 minuti luce).
T'²- X'² = -7,73² - 11,16² = -64,89
Come volevasi dimostrare la distanza spaziotemporale tra A e B è un invariante, ossia è uguale per tutti i sistemi di riferimento (attenzione che i valori riportati sono approssimati alla seconda cifra decimale, ma se si evitano le approssimazioni il risultato è preciso, ossia -64,89).
Un'ultima veloce considerazione: nella figura è stata indicata anche la luce che parte da B e raggiunge la Terra al tempo t= 10,3 minuti (2 + 8,3), mentre raggiunge l'astronave dopo circa 3,4 minuti dall'evento A (A visto dall'astronave avviene al tempo t' =0).
Lo stesso ragionamento si può fare per l'astronave rossa che viaggia dal Sole verso la Terra.
https://postimg.cc/image/ffdvb422d/
t'' = (t + vx) γ
t''a = (ta + vxa) γ e t''b = (tb + vxb) γ
Δt'' = (t''b – t''a) = (tb + vxb) γ - (ta + vxa) γ
Δt'' = ((tb -ta) + v (xb- xa)) γ
Δt'' = ((2 -0) + 0,8 (8,3- 0)) /0,6
Δt'' = (2 + 0,8 (8,3)) /0,6
Δt'' = (2 + 0,8 (8,3)) /0,6 = 14,4 minuti
x'' = (x + vt) γ
x''a = (xa + vta) γ e x''b = (xb + vtb) γ
Δx'' = (x''b -x''a) = (xb + vtb) γ - (xa + vta) γ
Δx'' = (xb + vtb - xa – vta) γ
Δx'' = ((xb -xa) + v (tb – ta)) γ
Δx'' = ((8,3-0) + 0,8 (2 -0))/0,6
Δx'' = ((8,3 + 0,8 (2))/0,6 = 16,5 minuti luce
Giusto per conferma nella figura l'intervallo di tempo Δt’' corrisponde a un intervallo misurato sull'asse del tempo t di 24 minuti (22 + 2 = 24).
Visto dal sistema di riferimento del terricolo, il tempo dell'astronave appare dilatato, ossia:
Δt'' = Δt 1/γ = 24 x 0,6 = 14,4 minuti
Inoltre per il sistema del terricolo (x=27,5) , anche lo spazio dell'astronave appare contratto:
Δx'' = Δx 1/γ = 27,5 x 0,6 = 16,5 minuti luce.
Anche in questo caso i risultati coincidono.
Inoltre la distanza spaziotemporale tra i due eventi non deve cambiare:
T''²- X''² = 14,4² - 16,5² = -64,89.
Quindi T² – X² = T'²- X'² = T''²- X''² .
Infine, rispetto a prima la luce che parte dall'evento B raggiunge l'astronave in un tempo decisamente maggiore rispetto all'altra astronave ed al terricolo...
Paolo
che dire? Paolo ne sa proprio una più del diavolo sulla RR. Sembra che quando cammini un po' rapidamente misuri tempo e distanza direttamente in RR e poi le trasformi in tempi e distanze "normali", con tutti i decimali del caso!!!!
Scherzi a parte... lasciatemi dire che Paolino è stato proprio chiarissimo, oltre che essere anche andato un po' oltre (ma su questa parte ci torneremo con calma).
Direi che fra tutti, il quiz è stato sviscerato appieno e posso tranquillamente ripetere la risposta, spostando soltanto l'origine degli assi sulla Terra e sul Sole nei casi di andata e ritorno. Piccolezze, ma tanto per cambiare qualcosa.
Aggiungo i due diagrammi nel riferimento dell’astronave. Spero che questa volta siano corretti.
Astronave in viaggio dalla Terra al Sole
Astronave in viaggio dal Sole alla Terra
E1: evento eruzione sulla Terra
E2: evento brillamento solare
E1A: evento simultaneo ad E1 nel riferimento astronave
E1S: evento simultaneo ad E1 nel riferimento Terra-Sole
E2A: evento simultaneo ad E2 nel riferimento astronave
u: velocità del Sole e della Terra rispetto all'astronave che è ferma in questo riferimento
u=-v, cioè è uguale ed opposta alla velocità dell'astronave nel riferimento Terra-Sole
L’intervallo di tempo che cerchiamo è quello tra gli eventi E1 ed E2 indicato con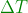
.
Il metodo diretto per il suo calcolo è quello di utilizzare le trasformazioni di Lorentz.
Volendo trovarlo a partire dai diagrammi si può usare questo procedimento.
Dai diagrammi si nota che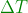
può essere visto come somma di due contributi 
.
Calcolo di
Quella che è l’intervallo di spazio tra Terra e Sole nel riferimento terrestre,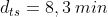
, nel riferimento dell’astronave diventa un intervallo con una componente temporale 
ed una componente spaziale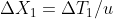
. Nel riferimento terrestre gli estremi dell’intervallo 
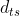sono simultanei essendo un intervallo di spazio. Gli eventi simultanei nel riferimento terrestre, nel riferimento astronave si trovano su rette che hanno la relazione 
tra le coordinate. Per questo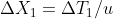 
. La distanza relativistica di un intervallo con le componenti che abbiamo detto è:
Nota: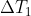
è dovuto al fatto che E1 ed E1S non sono simultanei nel riferimento astronave
Calcolo di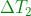
Lo stesso accade per l’intervallo temporale tra i due eventi E1 ed E2,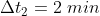
. Nel riferimento astronave questo intervallo ha una componente temporale 
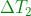ed una componente spaziale 
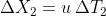. Nel riferimento terrestre gli estremi dell’intervallo 
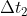sono spazialmente nello stesso punto (Sole) essendo un intervallo di tempo. Gli eventi spazialmente nello stesso punto nel riferimento terrestre, nel riferimento astronave si trovano su rette che hanno la relazione 
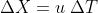tra le coordinate. Per questo 
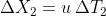. Ne segue che:
Calcolo di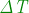
Sommando i due contributi si ottiene
Ovviamente è proprio una delle trasformazioni di Lorentz ed è lo stesso risultato ottenuto nel sistema di riferimento Terra-Sole. Non aggiungo il calcolo numerico che è lo stesso.