Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"

Sicuramente, un apporto fondamentale alla determinazione del pi greco o, se vogliamo, alla quadratura del cerchio si deve ad Archimede. Particolare importanza e suggestione ha il suo metodo meccanico a cui avevamo già accennato nell’articolo sul calcolo della superficie e del volume della sfera. Iniziamo a eseguire la quadratura di una parabola…

Questa serie di articoli avrebbe dovuto essere limitata al calcolo del pi greco attraverso i secoli. Tuttavia, nel cercare di mettere insieme tutto il materiale necessario si è giocoforza obbligati a imbattersi e a superare varie problematiche del tutto simili alla quadratura del cerchio, che mettono in luce la genialità dei grandi pensatori e geometri greci. A volte siamo di fronte a veri e propri capolavori “artistici” e risulta difficile trascurarli. Non per niente abbiamo affrontato la squadratrice di Ippia e la duplicazione del cubo.

Incontrando Euclide ci si accorge, poi, che è una vera miniera di idee e di previsioni fantastiche che solo l’algebra, molti secoli dopo, sarebbe riuscita a rendere più semplici e a dimostrare la sorprendente genialità che era già presente nell’antichità. Euclide merita sicuramente un discorso a parte e lo faremo sicuramente…

Si arriva, infine ad Archimede e le parole sono inutili. Le sue deduzioni e il suo metodo meccanico vanno descritti senza trascurare troppi dettagli, sia per l’importanza che hanno nella storia del pi greco sia per comprendere la bellezza e l’eleganza dei procedimenti usati da un personaggio che riusciva a ottenere risultati eclatanti solo con mezzi che chiamare “di fortuna” (oggi) sarebbe un’esagerazione.

In poche parole, prima di arrivare al cerchio (e al pi greco direttamente) mi sembra doveroso dare spazio al metodo di Archimede  e alla sua essenza fondamentale.

La leva e la bilancia sono gli strumenti indispensabili ad Archimede per risolvere meccanicamente un problema geometrico. Uno dei suoi capolavori è senz’altro la determinazione dell’area di un segmento parabolico. In parole povere, egli utilizza la bilancia per valutare i rapporti tra aree o volumi (assumendo, ovviamente, pari densità al materiale usato).

La base di tutto é la condizione di equilibrio rispetto a un fulcro (o punto di sospensione della bilancia). La vediamo nella Fig. 33.

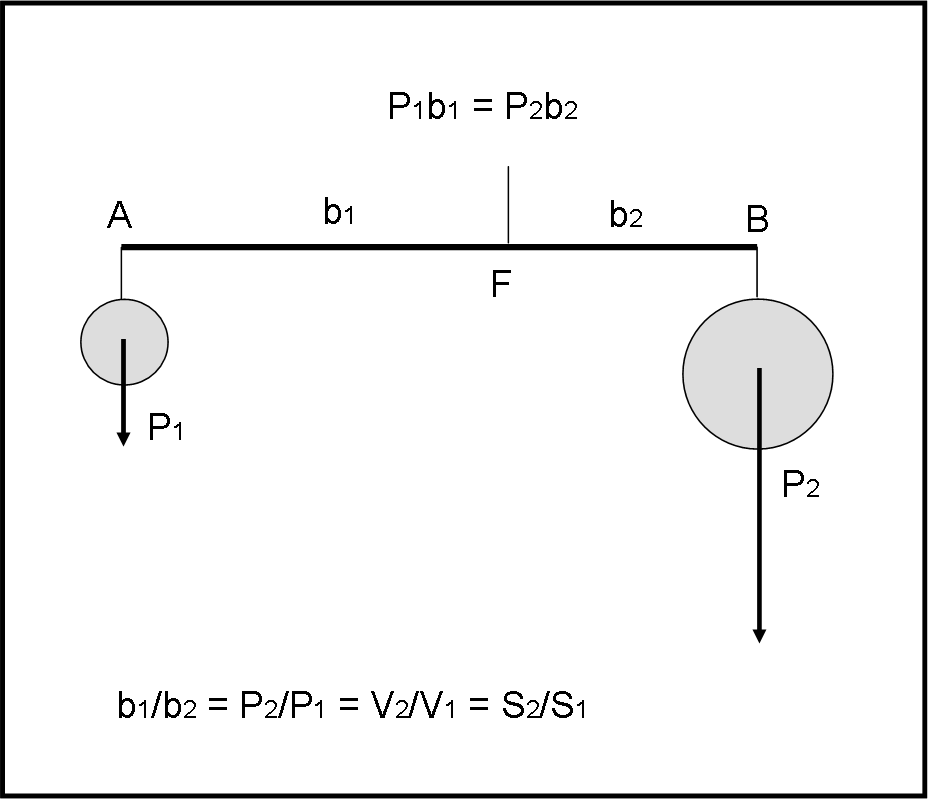
Se F è il fulcro della leva AB, le lunghezze dei bracci b1 e b2 sono inversamente proporzionali ai pesi P1 e P2 o, per densità costante, ai volumi V1 e V2 o, per figure piane, alle superfii S1 e S2.

In parole matematiche:

b₁/b₂ = P₂/P₁ = S₂/S₁ = V₂/V₁                …. (1)

Archimede considera questo metodo non rigoroso ma, a vantaggio degli altri matematici, fornisce esempi del suo valore efficace nel trovare aree e volumi; Il metodo possiede anche delle connotazioni filosofiche in quanto si pone il problema di considerare come un vincolo necessario, l'applicazione della matematica alla fisica. Archimede utilizza l'intuito per ottenere risultati meccanici immediati e innovativi, che poi però si impegna a dimostrare rigorosamente da un punto di vista geometrico, sfruttando soprattutto il metodo di esaustione, già introdotto da Eudosso e di cui parleremo in seguito.

Per capire al meglio lo spirito che anima Archimede, basta riportare la lettera a riguardo scritta ad Eratostene:

“Archimede ad Eratostene, prosperità!

Ti ho mandato precedentemente certi teoremi che avevo scoperto limitandomi a darti gli enunciati e invitandoti a trovare le dimostrazioni che io non avevo ancora indicato .... sono ora le dimostrazioni di questi teoremi che io ti invio redatti in questo libro. Ma prima, come ti avevo detto, dato che tu sei uno studioso e domini in maniera ragguardevole le questioni di filosofia e sai apprezzare nel suo giusto valore la ricerca matematica sui problemi nuovi che si presentano, ho giudicato opportuno di descrivere e di sviluppare in questo stesso libro le proprietà caratteristiche di un metodo che ti permetterà di affrontare certe questioni matematiche con l'aiuto della meccanica. Ma io sono persuaso che questo strumento può servire anche per la dimostrazione dei teoremi; certe proprietà in effetti, che mi erano apparse evidenti da un punto di vista meccanico, sono state poi dimostrate geometricamente, dato che, con questo metodo, non è possibile dare una dimostrazione rigorosa. E' più facile costruire una dimostrazione conoscendo preliminarmente le proprietà che si vuole dimostrare e che si sono conosciute con questo metodo piuttosto che cercare delle dimostrazioni senza nessun riferimento.”

 Al fine di una più immediata comprensione, noi faremo uso di formule algebriche e di geometria analitica, ma è bene sapere che certi risultati, oggi quasi immediati, sono stati ricavati da Archimede attraverso passaggi ben più complessi, che lui aveva riassunto nelle sue celebri proposizioni.

La quadratura della parabola (metodo meccanico)

Consideriamo un segmento di parabola e, per comodità, stabiliamo un sistema di coordinate cartesiane che ci permetta di fare semplici calcoli su di essa e su alcuni segmenti di enorme importanza. Riferiamoci alla Fig. 34.

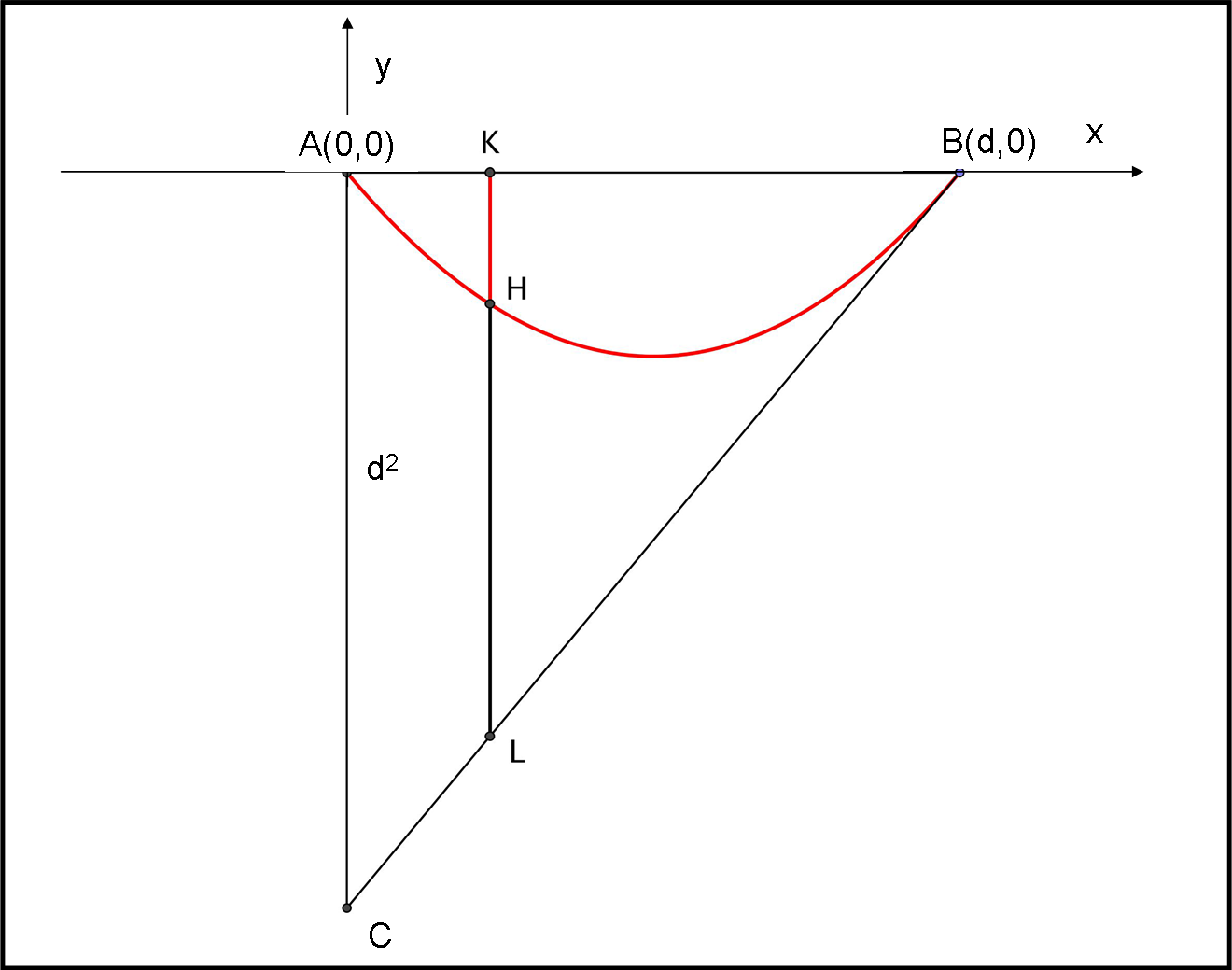
L’origine degli assi viene posto nel punto A e il segmento di parabola è quello che sta al di sotto dell’asse x. Costruiamo un triangolo rettangolo che abbia come cateto AB (punti d’intersezione della parabola con l’asse x) e per ipotenusa il segmento BC che sta sulla tangente alla parabola tracciata dal punto B (C è il punto di intersezione tra la tangente e l’asse delle y).

Iniziamo con scrivere l’equazione della parabola, assumendo l’ascissa di B uguale a d. La parabola ha equazione generica:

y = ax² + bx + c

Nel nostro caso passa per l’origine degli assi, per cui il termine c deve essere uguale a zero. Basta, infatti,  inserire x = 0 e y = 0 nell’equazione e si deriva subito che c = 0.

Sappiamo, inoltre, che per x = d , la y deve essere uguale a zero, ossia:

0 = ad² + bd = d(ad + b)

Dato che d > 0, deve essere

ad + b = 0

ponendo a = 1 (variando a varia la parabola, ma a noi interessa una parabola qualsiasi che passi per A e per B), si ottiene subito che:

b = - d

Da cui:

y = x² - dx = x(x - d)

Occupiamoci, adesso, della retta tangente in B alla parabola. Una retta qualsiasi ha equazione:

y = mx + n

Il passaggio per B, comporta che:

0 = md + n

Ossia:

n = -md

Non ci resta che ricavare m, ossia il coefficiente angolare della retta. Esso non è altro che la derivata della parabola calcolata nel punto B(d,0):

y’(d) = m = 2x – d = 2d – d = d

La retta ha quindi equazione:

y = mx + n = dx – md = dx - d²

y = d(x – d)

Si ricava anche subito l’ordinata del punto C, che si ottiene ponendo x = 0:

C (0, - d²)

Siamo arrivati al punto chiave del procedimento, di una genialità senza pari…

Tracciamo da un punto K qualsiasi dell’asse x (compreso tra A e B), una retta parallela all’asse y che intersechi la parabola in H  e la retta in L.

Quanto valgono KL e KH ?

Non sono altro che le ordinate corrispondenti all’ascissa x dei punti intersezione con retta e parabola, ossia:

KL = d(x – d)

KH = x(x –d)

Facendo il rapporto, abbiamo:

KL/KH = d(x – d)/(x(x – d)) = d/x

Possiamo semplificare dato che x ≠ d

Il rapporto x/d, però, non è altro che:

d/x = AB/AK

Si ottiene, perciò:

KL/KH = AB/AK

Immaginiamo, adesso, che sia KL che KH siano segmenti di un certo “peso”, ossia segmenti di metallo o di quello che volete, ma di uguale densità: la loro lunghezza è, quindi, proporzionale al loro peso.

Costruiamo una bilancia di fulcro A, che abbia un braccio (a sinistra) uguale ad AB e uno (a destra) uguale ad AK, come riportato in Fig. 35.

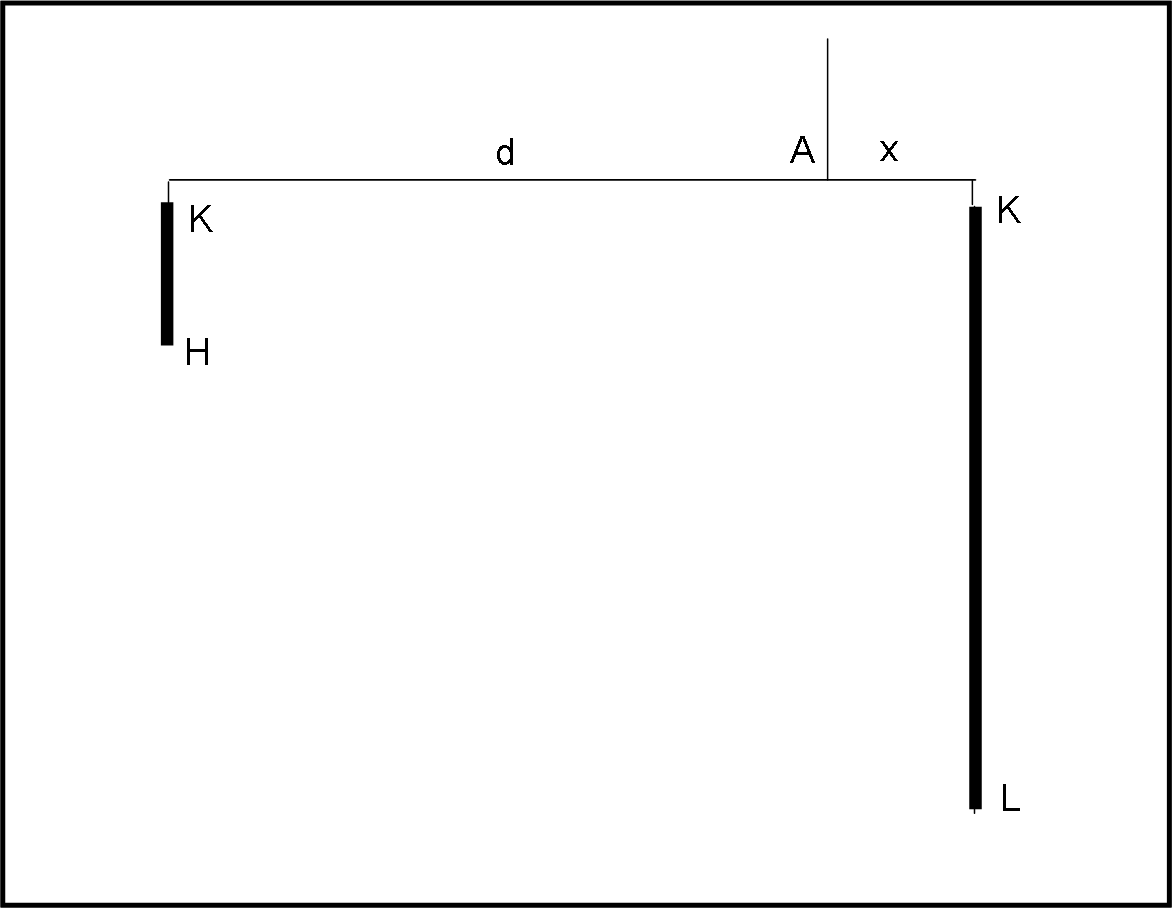
A distanza d = AB dal fulcro appendiamo il segmento KH. Mentre, dall’altra parte, a distanza x = AK appendiamo il segmento KL.

Per quanto stabilito per la bilancia di fulcro F dobbiamo ottenere un perfetto equilibrio. Infatti avevamo l’equilibrio per:

b₁/b₂ = P₂/P₁

che nel nostro caso diventa:

AB/AK = KL/KH

Proprio ciò che abbiamo ricavato nella (1).

Quanto fatto per i due segmenti, possiamo ripeterlo per l’intero triangolo e per l’intero segmento di parabola, in modo da mantenere l’equilibrio. Praticamente si costruisce il segmento parabolico appeso a sinistra e il triangolo a destra, attraverso sottili “fette” delle due figure geometriche. La distanza del braccio di sinistra è sempre AB, mentre il braccio di sinistra deve corrispondere al baricentro del triangolo (Fig. 36).

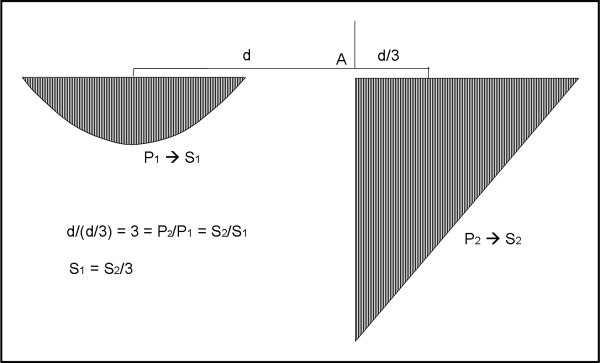
Ma Archimede sa benissimo dove si trova il baricentro di un triangolo: nell’intersezione delle mediane e, in particolare, a 2/3 dal vertice da cui è stata tracciata la mediana.

Da ovvi triangoli simili (Fig. 37) segue che il braccio a cui appendere il triangolo è uguale a 1/3 del braccio a cui si appende il segmento di parabola.

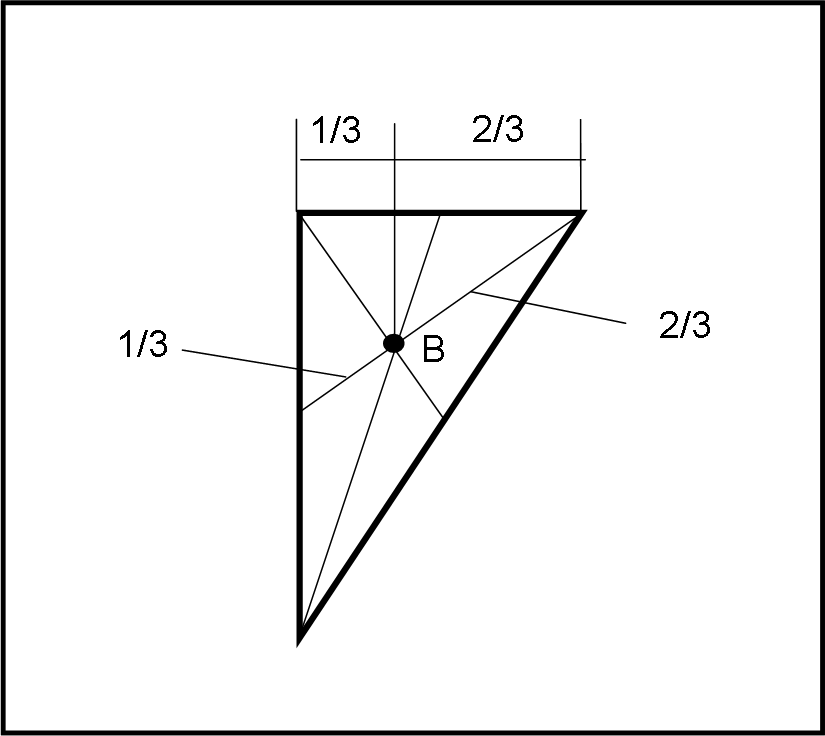
Ne segue che, avendo equilibrio, il peso, ossia la superficie del segmento di parabola è uguale a 1/3 della superficie del triangolo. Si è ottenuta la quadratura della parabola. Fantastico. In poche parole, abbiamo espresso l’area di un segmento curvilineo attraverso l’area di una figura le cui caratteristiche sono ben note. Si può fare ancora meglio (quel triangolo non è proprio l’ideale…).

Consideriamo di nuovo il nostro segmento di parabola e il triangolo ABC (Fig. 38). L’area di quest’ultimo vale:

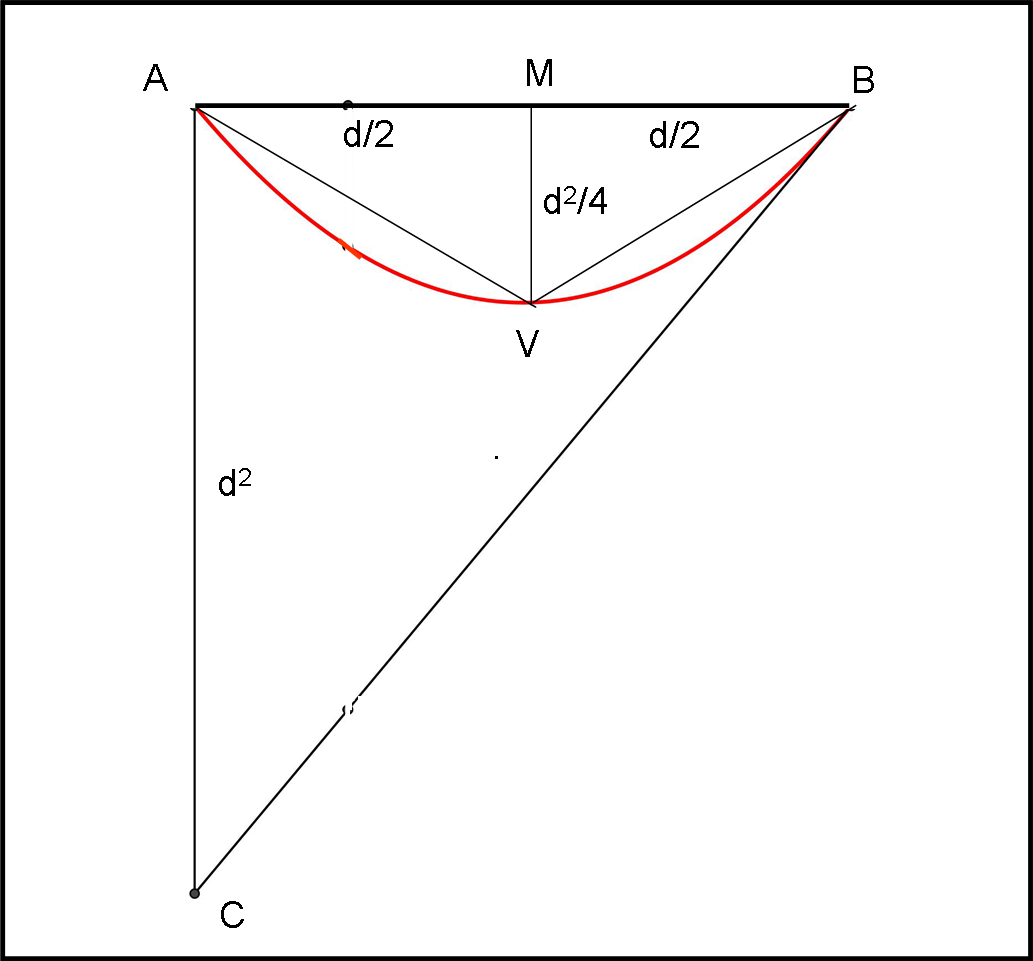
S_ABC = AB·AC/2 = d·d²/2 = d³/2

Ma sappiamo anche che è tre volte l’area S_P del segmento di parabola:

S_ABC = 3 S_P                .... (2)

Costruiamo, adesso, il triangolo ABV. Il vertice V ha come ascissa il punto medio di AB, ossia d/2.

L’ordinata di V vale:

y = x(x – d) = d/2(d/2 - d) = - d²/4

In valore assoluto possiamo scrivere che

MV = d²/4

Il triangolo ABV ha, perciò, un’area

S_ABV = MV·AB/2 = d³/8 = S_ABC/4

Ricordando la (2) si ha:

S_ABV = 3S_P/4

O, infine:

S_P = 4/3 S_ABV

L’area del segmento di parabola ha un’area che è 4/3 quella di un triangolo che ha la stessa e la stessa altezza.

Tutto ciò verrà poi dimostrato geometricamente attraverso il metodo di esaustione, lo stesso che servirà a quadrare il cerchio (non in modo classico… però), a cui abbiamo già accennato QUI.

La rettificazione del cerchio è stata invece trattata QUI, ma ci torneremo sopra sicuramente.

 

QUI gli altri articoli dedicati all'infinita storia del pi greco