Categorie: Fisica classica
Tags: accelerazione jerk moto velocità
Scritto da: Vincenzo Zappalà
Commenti:9
JERK: chi è costui? **
Questo articolo è stato inserito nella pagina d'archivio "Dinamica e meccanica", compresa in "Fisica classica"
Lo scopo di questo articolo è quello di affrontare la variazione dell'accelerazione e come questa e le sue sorelle di grado più elevato siano introdotte sia attraverso percorsi curvilinei alquanto laboriosi sia agendo sull'acceleratore e sul freno di un qualsiasi veicolo anche in moto rettilineo. In questa prima parte, decisamente più semplice, ci dedichiamo a un problema di pura cinematica.
Entriamo, dunque, senza timore nella cinematica più semplice e prendiamo come esempio un treno che deve partire dalla stazione P e deve arrivare nella stazione A che si trova a una certa distanza d.
Ciò che interessa, soprattutto, è riuscire a muovere il treno fermo in P. Se fossimo dei maghi (o -magari- se usassimo la meccanica quantistica) lo potremmo portare immediatamente in A. Nel grafico spazio-tempo (quello che ci serve per descrivere il moto) avremmo un salto repentino del treno dal punto P al punto A. Mostriamolo pure in Fig. 1.
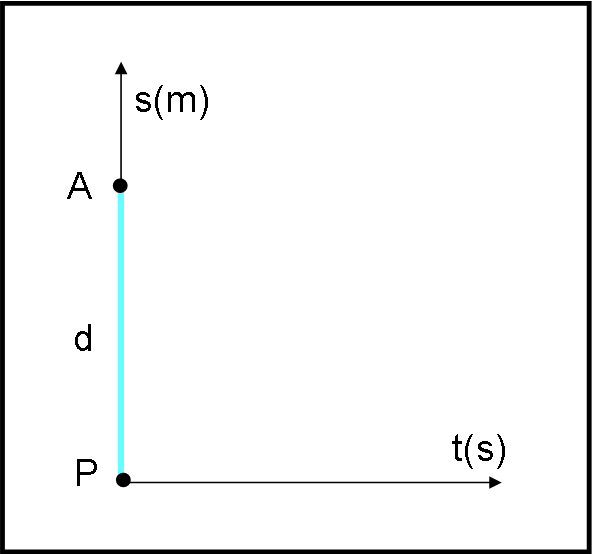
In un tempo uguale a zero il treno è sparito da P ed è comparso in A, più veloce della luce e di Superman. Ovviamente, per la nostra fisica, ciò non è possibile e ci dobbiamo accontentare di introdurre un moto più lento, ossia impartire al treno una certa velocità costante v0. La velocità può essere più grande o più piccola (senza avvicinare quella della luce se no addio cinematica semplice...) e il moto del treno è, di conseguenza, rappresentato da una retta inclinata che congiunge P con la stazione di arrivo, che dista d dal luogo di partenza. L'inclinazione della retta ci dice quanto velocemente il treno può raggiungere A, ossia quanto tempo impiega per percorrere la distanza tra le due stazioni.
Nel grafico spazio-tempo (Fig. 2) disegniamo questa retta del moto e nello stesso grafico inseriamo anche il valore della velocità che abbiamo scelto (cambiando l'unità di misura che non è più lo spazio, ma lo lo spazio diviso per il tempo, ossia m/s, metri al secondo). Non segniamo nemmeno le scale delle ascisse e delle ordinate, dato che vogliamo fare solo un discorso molto qualitativo e arrivare ai concetti fondamentali. Come vediamo la retta blu relativa alla velocità è una retta parallela all'asse del tempo, dato che è una costante. Notiamo, anche come il treno parta subito con un certo angolo (legato alla velocità) e come lo mantenga fino alla fine. Siamo nel caso di un moto rettilineo uniforme. Sicuramente un modo molto drastico per partire che è del tutto teorico, dato che la velocità non si può impartire con una bacchetta magica, ma deve essere raggiunta un po' alla volta. Non disegniamo più la stazione di arrivo A, dato che siamo interessati, per adesso, solo alla partenza. Notiamo anche che abbiamo tracciato la retta orizzontale della velocità "a casaccio" senza preoccuparci se ha proprio il valore che giustifica il moto del treno. Come ho detto, vogliamo solo capire i concetti.
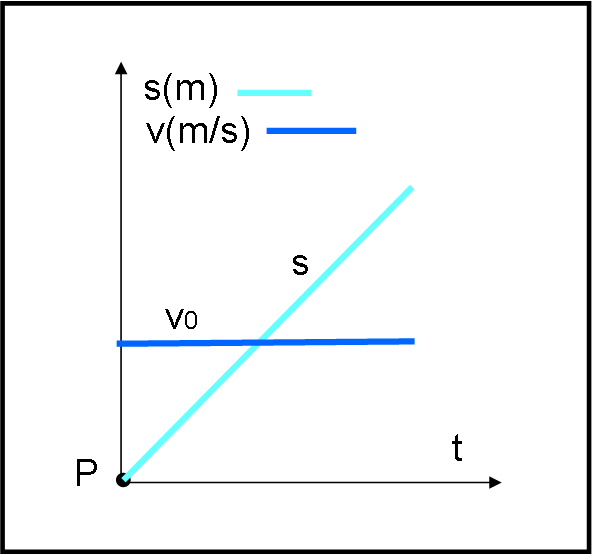
Passiamo allora a un caso leggermente più complicato. Vogliamo far crescere la velocità un po' alla volta in modo che il moto del treno avvenga lungo un curva spaziotemporale che parta in modo più tranquillo e più realistico. Introduciamo allora l'accelerazione. Essa (oltre a essere la derivata della velocità, ma questo lo vedrete nella seconda parte) è normalmente una costante, il che vuol dire che la velocità cresce in modo rettilineo e il moto del treno diventa parabolico o se preferite quello di una quadrica (funzione di secondo grado in t).
La Fig. 3 illustra la situazione, ove abbiamo inserito un nuovo asse delle ascisse relativo all'accelerazione, che si misura in metri al secondo al secondo (m/s2). Questa volta è l'accelerazione ad essere costante e la indichiamo con a0, colorandola in verde. Ovviamente, essendo costante, è una retta parallela all'asse del tempo.
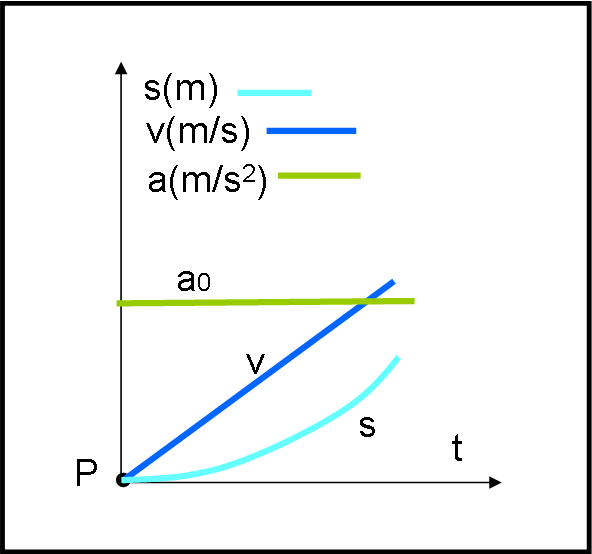
Anche se in modo qualitativo, possiamo già dire che l'introduzione dell'accelerazione costante ha fatto variare gradatamente la velocità e ha anche fatto muovere con molta più lentezza il treno, rispetto al moto rettilineo precedente (in cui il treno raggiungeva istantaneamente una determinata velocità). Continuando a mantenere l'accelerazione costante, il moto del treno diventerebbe, però, via via più rapido superando abbondantemente, dopo un certo tempo, lo spazio percorso da quello rettilineo uniforme. Come già detto, però, a noi interessa solo la partenza... e questa è stata "addolcita". In altre parole il moto è diventato un moto rettilineo uniformemente accelerato.
Normalmente lo studio del moto, in cinematica, si ferma qui... Ma noi vogliamo fare un saltino in avanti e aprire la strada per salti ancora più grandi.
Cosa vogliamo fare esattamente? Beh... la partenza del treno è abbastanza dolce (curva azzurro chiara), ma può essere ancora addolcita... Prima di passare all'azione vediamo la Fig. 4 che ci mostra l'andamento delle funzioni s = tn, con n crescente.
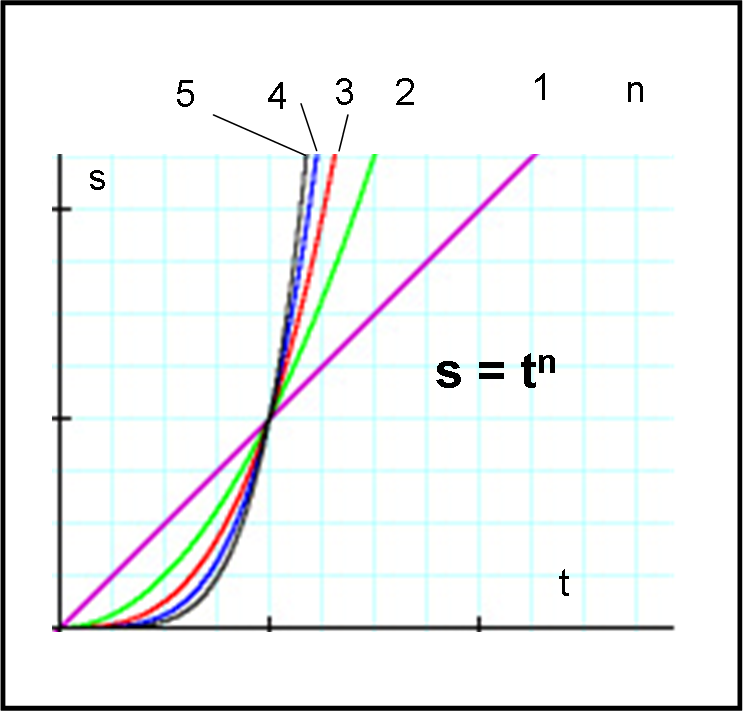
Per n = 1 e n= 2 abbiamo già visto il risultato, ma possiamo andare oltre e trarre una conclusione molto utile. Per n = 1 abbiamo la retta inclinata (che corrisponde al moto rettilineo uniforme); per n = 2 abbiamo una parabola (che corrisponde al moto rettilineo uniformemente accelerato). Notiamo subito quanto già detto; dopo un po' di tempo la parabola raggiunge e supera la retta, ma all'inizio (ossia alla partenza del treno) la parabola cresce più lentamente.
Una cosa analoga capita aumentando l'esponente n... le curve partono sempre con maggiore "delicatezza", salvo poi impennarsi sempre più velocemente. A noi basta e avanza, per adesso, quella con n=3. Potessimo far muovere il treno secondo quella curva la partenza sarebbe decisamente ancora più morbida. Come fare? Detto e fatto, basta far variare linearmente l'accelerazione. Questo fatto causa un moto secondo una curva del terz'ordine, una velocità che segue una curva del secondo ordine, un'accelerazione che assume l'andamento della retta inclinata, ossia del primo ordine, come mostrato in Fig. 5. Sì, ma se l'accelerazione è variabile deve esistere un qualcosa (la derivata dell'accelerazione) che è costante rispetto al tempo. Essa si misura in metri al secondo al secondo al secondo e viene chiamata JERK. Non vi è certo sfuggito che essa esiste ed è costante dato che il moto è una cubica (n = 3) e quindi la sua derivata terza è diversa da zero ed è costante.
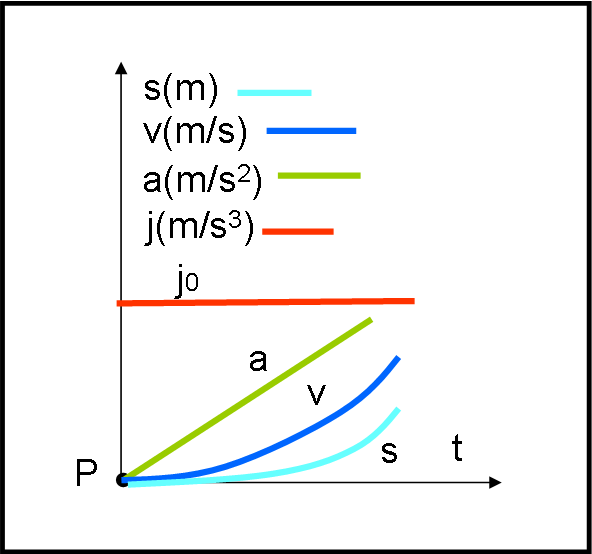
Non è difficile immaginare una curva del quart'ordine come moto e far variare linearmente anche lo jerk... ma, per adesso, a noi basta e avanza...
Abbiamo giocato in modo molto qualitativo, ma abbiamo capito come far partire il treno nel modo più dolce possibile e abbiamo anche introdotto la variazione dell'accelerazione. Non ci resta, adesso, che lavorare direttamente su un treno vero, facendolo partire e arrivare a destinazione senza causare tragedie. Per far ciò useremo tutte le strategie che abbiamo descritto precedentemente. Prendiamolo come un riassunto da seguire attentamente, dato che oltre ad accelerare dovremo anche decelerare...
Consideriamo la Fig. 5 e andiamo a commentarla con molta calma.
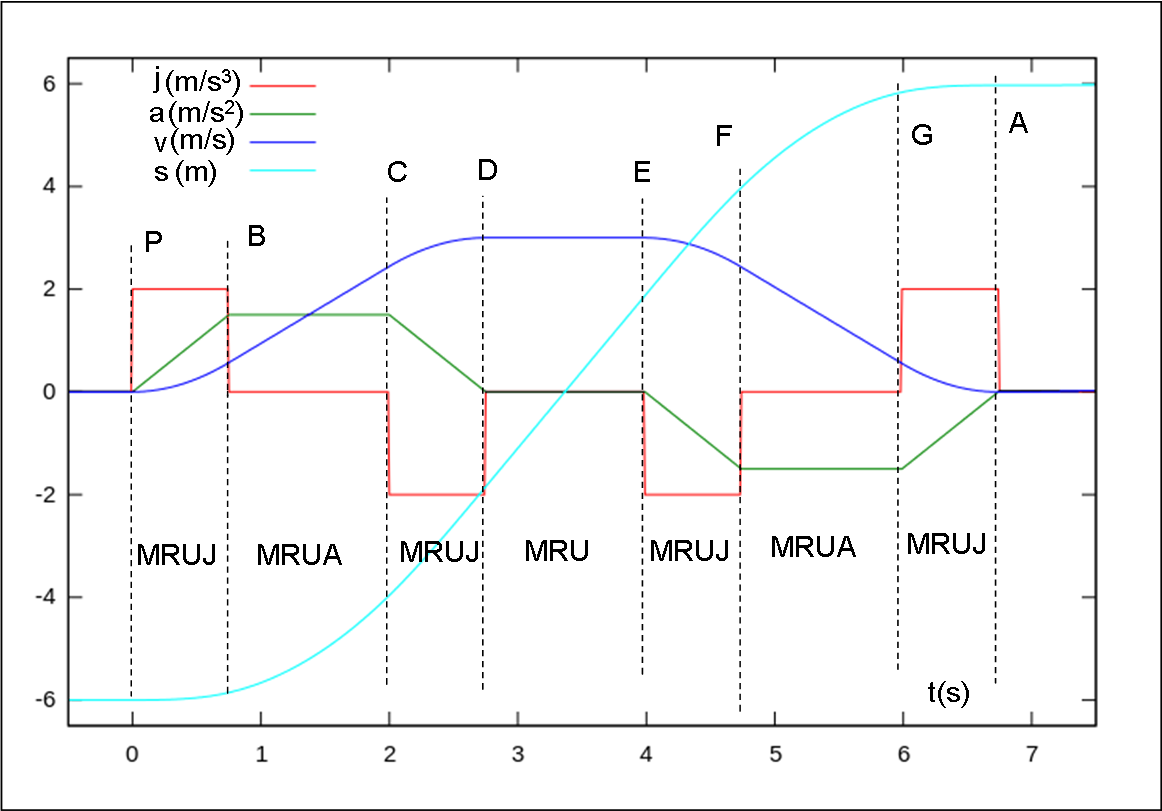
Come fatto precedentemente, nello stesso grafico sono state inserite le varie curve relative allo spazio, alla velocità, all'accelerazione, e al... jerk, in funzione del tempo. L'ascissa è sempre la stessa (t), ma l'ordinata cambia a seconda del colore (metri, m; metri al secondo, m/s; metri al secondo al secondo, m/s2; metri al secondo al secondo al secondo, m/s3)
Il moto può essere tranquillamente rettilineo (come andare in treno da una stazione a un'altra, percorrendo un solo lungo rettilineo), senza nessuna curva. Ciò che cambia non è il percorso, ma il modo di far procedere il treno dalla stazione di partenza P fino al suo arrivo nella seconda stazione A.
La curva azzurro chiaro rappresenta lo spazio percorso nell'unità di tempo. Il fatto che non sia rettilinea indica che il treno non viaggia certo a velocità costante, ossia il moto non è rettilineo uniforme, altrimenti avremmo una bella linea retta da A a P. O, almeno non lo è sempre. Possiamo vedere dove questo capita? Facilissimo: dove la curva azzurro chiara è una retta inclinata e dove la curva blu è una retta parallela all'asse del tempo (ossia è costante). Questo fatto capita nell'intervallo DE. In tale intervallo di tempo il treno viaggia di moto rettilineo uniforme (velocità blu costante). Ovviamente in questo tratto del percorso deve essere nulla sia l'accelerazione che il jerk.
Il moto, però non è nemmeno uniformemente accelerato (lo spazio seguirebbe una parabola). Nuovamente, vi sono dei tratti in cui lo è. Quali sono? Cercare i pezzi parabolici dello spazio è troppo complicato e non serve nemmeno: basta cercare i pezzi in cui la velocità cresce o decresce in modo rettilineo. Questo capita nel tratto BC e nel tratto FG. Nel primo la retta blu è inclinata verso l'alto, nel secondo verso il basso. Ciò vuol dire che nel primo tratto la velocità cresce, nel secondo decresce. In questi tratti l'accelerazione (linea verde) deve essere costante, ossia deve essere parallela all'asse del tempo. E' vero? Sicuramente sì. Nel primo tratto vi è un'accelerazione costante positiva, nel secondo negativa. Il primo tratto descrive un moto uniformemente accelerato, il secondo un moto uniformemente decelerato. Infine, in questi tratti, il jerk deve essere uguale a zero.
Normalmente si finisce qui lo studio cinematico di un... treno. Esso parte accelerando fino a raggiungere una velocità costante poi inizia a decelerare in vista della stazione successiva.
Nel nostro caso invece restano ancora quattro tratti da analizzare: PB, CD, EF e GA. Se guardiamo cosa succede alla curva azzurro chiara dello spazio, sembrerebbe avere a che fare con situazioni del tutto diverse tra loro. Nel tratto PB e GA è quasi parallela all'asse del tempo, ossia il treno percorre uno spazio piccolissimo nell'unità di tempo. Sembra quasi che qualcosa si opponga al movimento. Beh... è facile capirlo dato che in questi due tratti anche la velocità sta crescendo (PB) o decrescendo (GA) col la dovuta calma. E cosa può causare questo strano andamento? Sicuramente un'accelerazione non costante, ossia che tende a crescere in modo rettilineo. Nel primo tratto PB l'accelerazione sale ed è positiva, ossia va verso valori a mano a mano più elevati, costringendo la velocità a crescere anch'essa lentamente. Nel tratto GA l'accelerazione sale di nuovo, provenendo, però, da un valore negativo e quindi causa un "frenamento", dato che si avvicina allo zero. Se non si diminuisse gradatamente l'accelerazione , la velocità arriverebbe a zero troppo rapidamente. Siamo di fronte a due tratti rettilinei inclinati dell'accelerazione il che implica che la sua variazione deve però essere costante. Ma la sua variazione è proprio il jerk che infatti, nei due tratti analizzati, si sistema su un valore costante e positivo in entrambi i casi (accelerazione crescente).
Solo apparentemente diversi sono gli ultimi due tratti rimasti, CD ed EF. In entrambi i casi vi è una decelerazione rettilinea. In CD la motivazione è quella di smorzare lentamente l'aumento della velocità fino a portarla alla costanza. Nel secondo tratto, EF, la motivazione è quella di smorzare una sua repentina discesa. In entrambi i casi è necessario decelerare con una certa cautela, ossia in modo graduale. Variazione di accelerazione vuole di nuovo dire imporre uno jerk costante, che in questi casi sarà, però, negativo.
L'introduzione del jerk, ossia di una variazione dell'accelerazione effettuata linearmente evita passaggi troppo bruschi da una velocità a un'altra... Siamo comunque di fronte a un moto che in certi tratti non è uniformemente accelerato... al limite è uniformemente jerkato!
Se non avessimo introdotto il jerk, ossia avessimo impartito accelerazioni e decelerazioni costanti, avremmo sicuramente impiegato meno tempo tra le due stazioni, ma ci saremmo accorti di movimenti un po' troppo bruschi...
Nella figura sono stati segnate le varie parti descritte: moto rettilineo uniforme, MRU; moto rettilineo uniformemente accelerato, MRUA; moto rettilineo uniformemente jerkato (noi ci capiamo...), MRUJ.
Adesso che abbiamo compreso alcuni concetti base, possiamo studiare in dettaglio le variazioni delle variazioni e analizzare delle traiettorie veramente speciali che aiutino a ottenere i risultati voluti. Un discorso molto più da ingegnere che da matematico...
QUI la seconda parte






9 commenti
Molto interessante e chiaro.... grazie!
grazie a te, Mik!!
Maledetti schermi orizzontali! Mi sono slogato l'indice a scrollare su e giù la pagina tra il testo e i grafici! ;)
Comunque, of course, un mare di grazie per il gran bel post e l'intero gran bel sito.
Sai come puoi fare, Hotrats, per evitare di slogarti l'indice? E' semplice... basta aprire l'articolo in due finestre diverse: una la posizioni sulla figura che ti interessa e sull'altra fai scorrere il testo che la commenta.
Più o meno così...
Grazie Enzo, avessi avuto un insegnante di meccanica come te, non mi sarei mai dato al marketing!
@PapalScherzone
Non so se ringraziarti per la dritta o maledirti per avermi fatto capire quanto io sia rinc****nito ;)
Ciao
grazie amici di Circolo... e grazie anche a Scherzy
e grazie anche a Scherzy  per le sue idee continue (anche se spesso mi fa arrabbiare...
per le sue idee continue (anche se spesso mi fa arrabbiare...  )
)
Questi professori di astrofisica in pensione sono proprio incontentabili

E' risaputo che sono il papallo più buono sulla faccia della... Terra!