Categorie: Fisica classica
Tags: dinamica fluidi Feynman Reynolds turbolenza vortici
Scritto da: Maurizio Bernardi
Commenti:14
Il fascino discreto della turbolenza *
Questo articolo è stato inserito nella pagina d'archivio "Vortici e Turbolenze", che si trova sia nella sezione "Fisica Classica" che in "Forme ricorrenti nell'Universo"
Mentre state camminando sul marciapiede, ad un certo punto, vi trovate davanti un cavalletto che segnala lavori in corso ( hanno fatto una buca per riparare un tubo del gas) che vi impedisce di andare diritto. Dovete aggirarlo a sinistra o a destra.
Se siete già un po' a sinistra andate ancora più a sinistra, oppure se già siete un po' a destra vi spostate ancora più a destra. Naturalmente non siete obbligati, ma anche la natura sceglie la via più facile, di solito. Se siete proprio al centro, spero che non farete come l'asino di Buridano e troverete il modo di decidere.
Lo stesso problema ce l'hanno gli elettroni davanti alla doppia fenditura e sanno cavarsela egregiamente, lasciandoci tutte le perplessità sul loro comportamento.
Ma anche le molecole di acqua (o quelle dei gas che compongono l'aria, o gli stormi di uccelli) si trovano nella medesima situazione, quando incontrano i piloni di un ponte.
C'è chi va a sinistra e chi va a destra, ma a differenza di voi, non sono soli, a dovere prendere rapidamente la decisione, sono una moltitudine.
Chi si trova oltre il bordo dell'ostacolo, su un lato o sull'altro, andrà proprio diritto per la sua strada, magari un po' disturbato dal vicino, che sceglie la medesima direzione, spostandosi un po' verso di lui. Ma se i vicini sono molti, quelli più centrali si dovranno spostare di un bel po', proprio la metà della dimensione dell'ostacolo. E' improbabile che chi si trova più o meno al centro, ma verso il lato opposto, faccia la scelta illogica di spostarsi nella direzione più lontana, ma non si sa mai.
Inevitabilmente si manifesterà una pressione trasversale, per via di quel 50% di folla che deve evitare l'ostacolo, aggirandolo su quel lato.
E' come se si mettessero in coda, in direzione perpendicolare, rallentando il moto naturale che avevano, per girare intorno a quel benedetto pilone. Voi avete il vantaggio di vedere l'ostacolo prima di andare a sbatterci contro, e potrete anticipare la deviazione, ma se foste attorniati da altri...
Saranno educate queste molecole? saranno ordinate? diranno "Prima lei, signora..." , "Ma si figuri, passi pure lei, io non ho fretta", oppure si affastelleranno nell'ansia di non restare bloccate davanti all'ostacolo, senza troppi riguardi l'un l'altra?
E che traiettoria seguiranno, dopo? Cercheranno di ridurre la pressione che le circonda, tornando, a pilone superato, nella posizione che avevano prima? Dovrebbe essere facile farlo, perché all'ombra dell'ostacolo lo spazio è libero e sicuramente costituisce una attrattiva. Ma come riempiranno quello spazio? Ordinatamente, andando ad occupare proprio la "corsia" in cui erano prima, oppure si spintoneranno nella fretta di infilarsi in qualsiasi modo in quel vuoto che si ritrovano lateralmente?
Non occorre essere una molecola d'acqua per saperlo, basta essere stati anche solo una volta in coda in autostrada, o al supermercato, quando arriva l'annuncio "apre la cassa 11" e osservare i movimenti e le manovre tattiche dei clienti già in coda alle casse adiacenti la 11.
Se però vi siete fissati di capire come si comportano le molecole d'acqua, basta osservarle.
Lo faceva anche Leonardo.

E poi lo hanno fatto anche altri, per esempio Feynman, come vedete.
E se vi interessa leggere che ne dice, basta andare qui, alle sue straordinarie lezioni californiane. http://www.feynmanlectures.caltech.edu/II_41.html
A proposito, quest'anno è il centesimo anniversario della sua nascita.
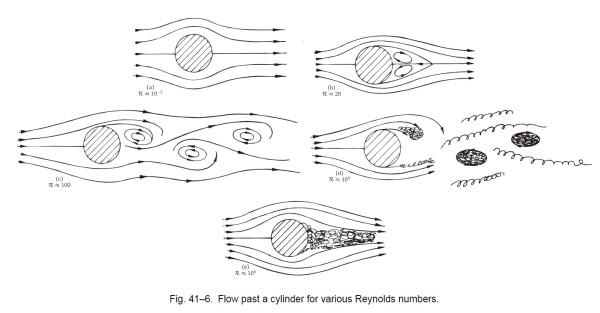
Dunque, questa figura 41-6 dice … Flusso a valle di un cilindro per diversi numeri di Reynolds...
Ma chi è questo Reynolds? E cosa sono quei suoi numeri?
Osborne Reynolds, un fisico e ingegnere nord-irlandese, studiò, oltre un secolo fa, i moti laminari e i moti turbolenti di un fluido in un condotto.
I moti laminari sono quelli in cui il fluido scorre lungo piani paralleli ed ogni particella si mantiene, anche a livello microscopico, sempre sul medesimo piano, senza interagire con quelle dei piani adiacenti.
Il moto turbolento, viceversa, presenta dei vortici di dimensione e velocità differenziate, imprevedibili. Se sapessimo risolvere esattamente le equazioni che lo descrivono (equazioni di Navier Stokes) e conoscessimo perfettamente la distribuzione delle velocità, potremmo in teoria prevedere tutti i valori futuri, ma nella realtà il livello di precisione con cui possiamo conoscere tali valori non è assoluto e, trattandosi di un moto caotico, minime differenze iniziali producono risultati del tutto diversi e imprevedibili.
In base ai risultati ottenuti, Reynolds giunse alla definizione di un valore caratteristico, detto appunto numero di Reynolds, (Re, un numero puro) che dipende essenzialmente dai valori di densità ρ del fluido (ad una certa pressione e temperatura) di viscosità μ e di velocità media del flusso v , oltre che dal diametro d del condotto.
Ricordiamo che la densità non è altro che la massa rapportata al volume, mentre la viscosità è la resistenza allo scorrimento che si manifesta tra una lamina di fluido e quelle adiacenti.
L'espressione è questa: Re = ρ v d / μ
Restando a livello intuitivo, questo numero è quindi proporzionale a quanto è denso e veloce il fluido e a quanto è grande il diametro della tubazione in cui scorre, mentre è inversamente proporzionale alla sua viscosità.
Esiste un valore critico di Re che separa il regime laminare da quello turbolento, in cui si creano i vortici, che non sono sfuggiti all'occhio indagatore di Leonardo.
Il movimento di un fluido, oltre che entro una tubatura, può avvenire attorno ad un corpo, ( o il corpo può muoversi dentro il fluido). Anche in questi casi, a seconda della velocità e degli altro parametri, otterremo un preciso valore del numero di Reynolds.
Così vediamo, nei disegni di Feynman, a numeri di Reynolds diversi corrispondono configurazioni diverse del fluido a valle del corpo con cui ha interagito.
Nel primo disegno Re vale 10-2 e non si formano vortici: il regime rimane laminare.
Nel successivo, con Re= 20 vediamo una coppia di vortici apparire a valle dell'ostacolo.
Nel terzo disegno con Re = 100 i vortici si distaccano e creano una scia, che prende il nome di Scia di Von Karman, una configurazione che genera una vibrazione dell'ostacolo, dovuta alla variabilità della pressione determinata della doppia coda di vortici alternati e inframmezzati ai due lati.
La possiamo apprezzare in questa animazione tratta da Wikipedia.

Come potete immaginare, lo studio di queste vibrazioni è fondamentale per la progettazione di strutture immerse in una corrente di fluido, come nel caso delle piattaforme petrolifere o dei ponti, ma anche nel caso di edifici come grattacieli esposti ai venti.
Una strategia per contrastare questo fenomeno, che potrebbe produrre dannosi effetti in caso di risonanza con le frequenze critiche delle strutture, è di inserire elementi a forma di pinna che evitano la formazione delle scie vorticose. Nel caso di edifici o tralicci, che possono essere esposti a venti di direzione imprevedibile, si ricorre a elementi a profilo elicoidale, simili a filetti che, montati sulla superficie delle strutture, generano un flusso asimmetrico tridimensionale che riduce la formazione alternativa dei vortici.
Il fenomeno si presenta anche nelle strutture degli impianti petroliferi, in cui i vortici generati dalle correnti marine esercitano una forza di sollevamento che agisce lungo la superficie immersa dei tubi di pompaggio, attraverso i quali gli idrocarburi estratti vengono pompati fino alla piattaforma galleggiante.
In questa immagine si vede distintamente la struttura elicoidale che riduce gli impatti dovuti alla formazione della scia di von Karman e conseguentemente l'effetto di sollevamento.

Ecco alcune fotografie che illustrano una sequenza analoga ai disegni tracciati da Feynman.
Ciò che varia è essenzialmente la velocità del flusso, crescente di fotogramma in fotogramma, a cui il numero di Reynolds è direttamente proporzionale.
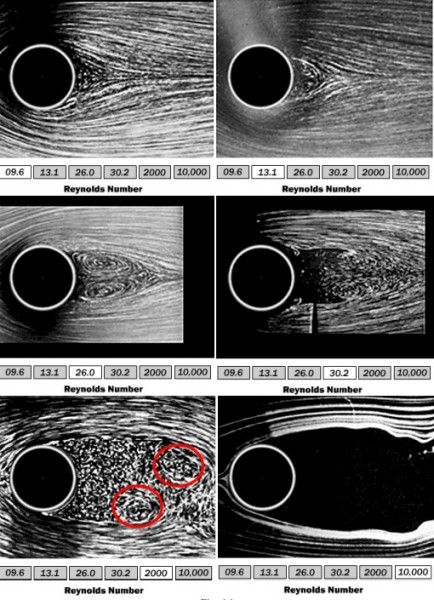
Cosa c'è nei circolini rossi?
Ebbene, in questo caso il numero di Reynolds è molto elevato, vale 2000, ma i vortici che si vedono distintamente separati, sono proprio quelli della scia di Von Karman, che abbiamo già visto.
Feynman ce li mostra ad un numero di Reynolds ancora più grande : 104 e mette bene in evidenza che i sensi di rotazione delle due famiglie di vortici sono opposti.
Ce lo fa vedere anche con questa interessante fotografia:

La formazione dei vortici avviene a cascata, vortici grandi generano vortici più piccoli con un meccanismo di autosomiglianza frattale.
Se non vi è chiaro il significato di autosomiglianza frattale basta che andiate da un fruttivendolo e compriate un cavolfiore come questo.

Se ne staccate una parte ritroverete in miniatura la medesima struttura dell'intero. E una parte di quella parte manterrà l'identica somiglianza, insomma, una autosomiglianza.
Allo stesso modo nei vortici potrete ritrovare vortici più piccoli e ancora più piccoli, e così via. Come in questa immagine.

L'energia si trasferisce dai vortici maggiori a quelli secondari e poi ai più piccoli e ancora più piccoli, fino a raggiungere un limite in cui si trasforma in calore ceduto all'ambiente. Tornate un momento al disegno di Leonardo e potrete notare che Lui lo aveva capito perfettamente, i vortici sono presenti in una mescolanza di dimensioni.
La vorticosità nei regimi turbolenti è un fenomeno estremamente complesso, che ad oggi non ha trovato risposte definitive, nonostante i progressi fatti. L'impiego di simulazioni numeriche e di modelli fisici è indispensabile per superare i limiti e le carenze dell'approccio teorico.
Ai confini del caos, la turbolenza rappresenta tuttora una grande sfida: pur trattandosi di un fenomeno perfettamente ambientato nella fisica classica, pur non necessitando di concetti di fisica moderna, come la meccanica relativistica o la meccanica quantistica, e pur disponendo della descrizione matematica delle leggi fondamentali che la governano, (equazione di Navier-Stokes) siamo ancora alla superficie di una comprensione completa.






14 commenti
Chissà perché ho subito pensato a questo...
Qualsiasi riferimento è del tutto casuale (oppure no ?)...
Caro Enzone, so che mi crederai...
Era una immagine candidata ad essere messa in evidenza in testa all'articolo.
Grazie di averla "recuperata" nel tuo commento.
E io recupero l’articolo in cui è inserita quella splendida immagine, oltre a consigliarne vivamente la lettura a chi se lo fosse perso
http://www.infinitoteatrodelcosmo.it/2014/05/15/da-van-gogh-alla-macchia-rossa/
E quella gif animata a me ha fatto pensare a questo:
Ciao a tutti
Grazie hotrats, splendida immagine dal satellite dei vortici generati dalle isole di Capo Verde, che fa riflettere su quanto la bellezza sia unita al pericolo in questi "attraenti" fenomeni naturali.
Pericolo. Poi prometto che non parlerò più di aerei, ma quanto al pericolo delle scie vorticose volevo solo ricordare che la torre autorizza il decollo solo dopo due minuti dal precedente. La turbolenza che genera un aereo di linea specialmente nelle fasi di decollo e atterraggio, con la configurazione "sporcata" da flap, slot, ecc. è tale che può addirittura capovolgere un velivolo più leggero che lo segua. Si vola in sicurezza solo mantenendo una quota maggiore di chi ti precede perché le scie che si staccano dalle sue ali e fusoliera tendono a scendere (per gravità? ). In aria molto umida la turbolenza diventa spesso visibile a causa della decompressione adiabatica che la raffredda è condensa, tanto da far credere ai profani che si tratti di un principio d'incendio.
Per non parlare degli effetti anche catastrofici della turbolenza che possono provocare i grandi ostacoli come alberi, edifici e peggio ancora montagne. Sottovento a queste si formano dei rotori che un piccolo velivolo non riesce proprio a contrastare. Puoi solo abbandonarti ad essi come una foglia al vento affidandoti alla tua buona sorte. A me è successo un paio di volte e lo ricordo bene
Caro Alberto, invece dovresti promettere di parlarci ancora di queste esperienze di fenomeni così poco familiari alla maggioranza delle persone. L'aria, a differenza dell'acqua, non si vede, ma la sua azione non è meno vigorosa e talvolta devastante. Chi come te si è confrontato con questo elemento ne ha una percezione fisica che va certo ben oltre la comprensione teorica di qualche equazione. Grazie.
E mi sono dimenticato di ricordare la tremenda turbolenza all'interno dei cumolonembi. Se un aereo ci entra, a parte che può essere distrutto da chicchi di grandine piu' grossi di noci, può ritrovarsi tirato su o giù per migliaia di piedi in pochi secondi.
Un mio conoscente andava davanti al cumulonembo a seminare sali d'argento per scongiurare la grandine. Riduceva il motore al minimo e si lasciava trasportare come una foglia. Non so se sia ancora vivo
Grande! Ero sicuro che ci fossero altre cose da sentirti raccontare.
Già che ci sei leggi anche questo...
http://www.infinitoteatrodelcosmo.it/2018/09/22/nuove-storie-turbolenza/
Si parla anche di uno strano aereo.
Ioduro d'argento
restando a livello più "terrestre" e conosciuto...
http://www.infinitoteatrodelcosmo.it/2015/02/22/pirlo-tira-e-segna-il-merito-e-di-bernoulli/
Guardate che bei vortici di Karman si sono formati ieri a sud-ovest delle Canarie. In particolare l'artefice è il vulcano Teide, a Tenerife, alto ben 3.700 metri slm. Screenshot ricavati dall'app Windy impostata su Satellite.
Una vera meraviglia !
Ringrazio Alberto per averci fatto notare questo fenomeno che io non conoscevo.
Per quanto ho letto dopo il commento di Alberto, probabilmente il fenemeno è anche dovuto alla inversione termica presente nella zona oltre alla presenza del vulcano segnalata da Alberto.
Nella figura c’è la situazioni del 24 febbraio alle 12:00 UTC.
In effetti c’è una inversione termica a relativamente bassa quota (linea a destra) e vento a bassa quota circa nella direzione dove si sono formati i vortici.
Le nuvole che rendono visibili i vortici dovrebbero essere vicine a terra, al di sotto dell’inversione termica. L’inversione termica ostacola l’ascesa dell’aria che non riesce a “scavalcare” il vulcano ed è costretta ad aggirarlo producendo i vortici.