Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

La definizione degli spazi compatti è stata introdotta un po' al volo. Per cui volevo approfondire  il discorso, cercando di dare spiegazione a due fatti fondamentali che ci permetteranno di andare avanti con le nostre costruzioni topologiche in tutta tranquillità: la compattezza dell'intervallo chiuso in R e del quadrato (o rettangolo) in  .

La definizione data di compattezza è topologica,  è la più generalizzata, ed è stata introdotta così perchè sia valida appunto anche negli spazi topologici. Tale definizione di spazio compatto è diversa negli spazi metrici, dove si usa la convergenza di successioni. Ma negli spazi topologici, abbiamo a disposizione solo gli aperti, e dobbiamo usare quelli.Riprendiamo ora la definizione di spazio compatto.

Ricoprimento aperto di uno spazio topologico

E' una famiglia di aperti  tali che .

Sottoricoprimento finito di U

è una parte della famiglia U, consistente in un numero finito di insiemi , tali che la loro unione contenga ancora X:

 tali che valga ancora , e l'insieme degli indici J, oltre ad essere un insieme finito, sia sottoinsieme di I.

Definizione di spazio  compatto

Uno spazio topologico X è compatto se e solo se da ogni ricoprimento aperto U è possibile estrarre un sottoricoprimento finito V. 

Di sicuro decidere se un insieme topologico è compatto o no, non è la cosa più semplice di questo mondo. Faremo un esempio di spazio compatto spostandoci su R, che è uno spazio metrico. Scopo principale di questo articolo è dimostrare che l'intervallo [0,1] è compatto.

Ma cominciamo dall' inzio; siamo in R che è uno spazio metrico e dobbiamo trattare con degli aperti. Riporto la definizione che avevo dato di aperti negli spazi metrici:

Insiemi aperti negli spazi metrici.

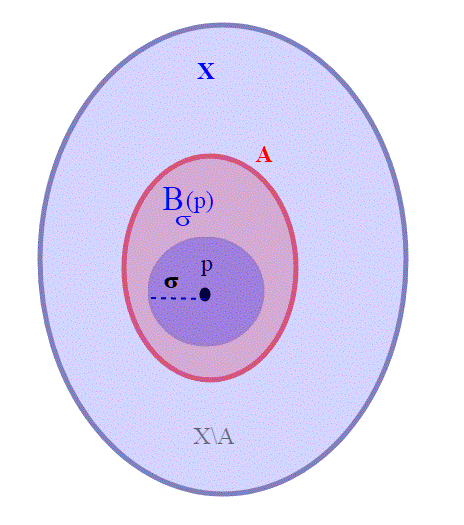
Dato un insieme X con la sua metrica d, definiamo un sottoinsieme

 aperto, se comunque scegliamo un punto p appartenente ad A,

, esiste una bolla con centro in p contenuta in A, ovvero più formalmente, esiste un >0 tale che:

. Nel caso di R sappiamo che le bolle sono gli intervalli aperti centrati in p,  . Ricordo poi che anche intervalli (a, b) sono insiemi aperti mentre quelli di tipo [a, b] non sono aperti (infatti ogni bolla di centro b esce fuori dall’ intervallo [a, b] e quindi non vi può essere contenuta).

 

Un altro concetto che ci servirà, e che anzi sarà la chiave della dimostrazione è quello di estremo superiore in R. Avevamo parlato di R e della continuità nella serie dedicata agli infiniti di Cantor. Qui trovate l'articolo, io riprendo solo quello che ci serve per la dimostrazione. Per no appesantire troppo l'articolo, ho dato la possibilità di aprire o no dei dettagli.

Per chi non ha letto i dettagli sopra ricordiamo la proprietà fondamentale dell'estremo superiore:

Se M è l'estremo superiore di un insieme S , allora esistono elementi di S arbitrariamente vicini a M=sup S.

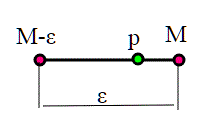
O detto in modo più formale:

Qualsiasi sia il numero , esiste sempre un elemento p di S tale che M-p<

Veniamo adesso alla nostra dimostrazione:

L’intervallo I = [0, 1] con la topologia indotta da quella euclidea è uno spazio topologico compatto.

Sia   un ricoprimento aperto di [0,1] , ovvero   . Sia N un numero reale maggiore di 1 (N>1). Sia S l'insieme dei   tali che esiste un sottoricoprimento finito di U che copre l'intervallo [0,k].

Tale insieme è non vuoto perchè . Infatti U ricopre tutto [0,1], quindi esiste un  che contiene lo zero, e quindi anche [0,0]. {}  è un ricoprimento finito di [0,0]  che consiste solo nell'insieme  stesso. S è superiormente limitato; infatti gli elementi di S non possono essere maggiori di N, dovendo appartenere a [0,N].  Quindi esiste l'estremo superiore. Sia M=supS . M è maggiore di 1.Supponiamo per assurdo M<=1.

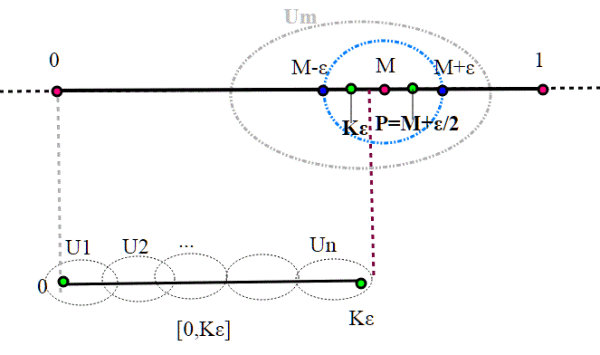
M è un punto di [0,1], quindi è contenuto in qualche aperto Um del ricoprimento. Essendo Um aperto, esiste un intervallo aperto contenuto in Um e centro in M, ovvero un intervallo aperto (M-ε,M+ε)  contenuto in Um. E qui interviene il concetto di estremo superiore; essendo M estremo superiore, esiste un  che sta fra ;

Ma allora, appartenendo ad S, esiste un sottoricoprimento finito di U che  contiene 

U1,U2,....Un, ovvero

Prendiamo adesso un punto P interno a , che potrebbe essere per esempio , tanto per fissare le idee.  (qualsiasi punto interno a  andrebbe comunque bene).

Se adesso noi aggiungiamo a tali insiemi aperti anche l'insieme Um , avremmo che anche [0,M+ε/2] ammette un sottoricoprimento finito.

Infatti [0,M+ε/2]=[0,] U [t,M+ε/2]   [0,] U (M-ε,M+ε)  

Ma questo è assurdo, in quanto M è estremo superiore di S,  mentre M+ε/2 è maggiore di M e appartiene ad S.

Quindi M>1. Ma se M>1, per la proprietà dell'estremo superiore, esiste K  tale che 1<K<M (basta prendere )

Quindi K appartiene ad S, ed esiste un sottoricoprimento finito di U  che lo contiene. Ma allora, essendo 

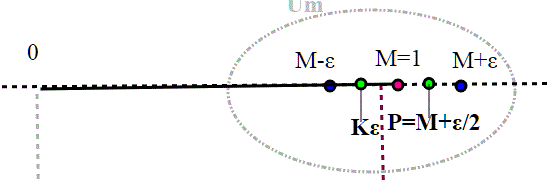
,esiste un ricoprimento finito per [0,1] che quindi è compatto. Notare che il disegno è stato fatto nel caso M<1; niente cambia se M=1:

 

Notiamo che il fatto che [0,1] sia compatto dipende esclusivamente dalla continuità di R. In Q (razionali) , questa dimostrazione non sarebbe valida, in quanto non vale l'assioma di completezza.

Tutti gli intervalli di R chiusi, del tipo [a,b] sono compatti.

Infatti, come abbiamo visto nell'ultimo articolo:

Sia f : X--->Y un’applicazione continua, e sia X uno spazio compatto. Allora f(X) è uno spazio compatto.

Sappiamo che gli intervalli  [0,1] e [a,b] sono omemorfi, quindi esiste una applicazione continua di  [0,1] ---> [a,b].

Citiamo ora un Teorema che non dimostreremo.

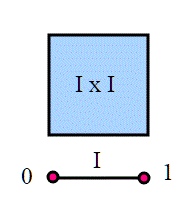
Siano X, Y degli spazi topologici. Allora L'insieme prodotto X x Y è uno spazio topologico compatto.

Ma allora veniamo al nostro quadrato [0,1] x [0,1], o più in generale al rettangolo  [a,b] x  [c,d]. In base al teorema citato, tali  sottoinsiemi di  sono compatti.

Il Teorema di Heine-Borel.

Per chi vuole andare più a fondo sui compatti di ,  esiste un risultato molto potente, Il Teorema di Heine-Borel. Esso parla di insiemi chiusi (e questo sappiamo cosa vuol dire) e limitati (questo invece no). Intuitivamente (e anche formalmente), un insieme Y è limitato se riusciamo a contenerlo con una bolla di un certo raggio N. Ebbene, il teorema afferma che:

Un sottoinsieme Y di  è   compatto se e solo se Y è chiuso e limitato.

La dimostrazione non è molto difficile, usando i risultati visti sopra. Il fatto che [0,1] sia compatto è infatti alla base della dimostrazione.Ma per ora la omettiamo. Notiamo che sia l'intervallo chiuso che il rettangolo sono insiemi chiusi e limitati.

Bene, adesso che sappiamo che gli intervalli  chiusi e i rettangoli sono compatti, possiamo andare avanti con le costruzioni della topologia quoziente.