Categorie: Fisica classica
Tags: equazione di Tsiolkovsky moto del razzo quantità di moto seconda legge della dinamica
Scritto da: Vincenzo Zappalà
Commenti:7
Lanciamo un razzo ***
Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.
Uffa! Basta relatività ristretta... Torniamo alla cara, sana e semplice (?) meccanica classica. Ma non illudetevi troppo, perché Minkowski è sempre in agguato... Il problema che affrontiamo si ricollega a quello più generale della legge del moto di un corpo di massa variabile. Noi lo trattiamo nel caso più semplice, ossia quello di un razzo che non subisca forze esterne durante il suo movimento.
Un sistema a massa variabile significa, in parole povere, un sistema materiale che durante il suo moto aumenta o diminuisce la propria massa con il tempo. A prima vista sembrerebbe sufficiente utilizzare la seconda legge di Newton. In realtà la massa diventa una variabile ed è necessario “riscriverla” in modo da tenere conto della quantità di moto che viene aggiunta o tolta a seguito dell’aumento o della diminuzione della massa del sistema. Un problema non eccessivamente complesso che trova la sua migliore applicazione nel moto di un razzo. Inoltre, come avrete già capito, è un problema che mi piace moltissimo, dato che vede come attore principale proprio la mia grandezza fisica preferita: la quantità di moto!
Iniziamo con un minimo di storia. Si immagina, generalmente, che il moto di un razzo sia strettamente collegato ad episodi bellici, come le celebri V2 tedesche potrebbero facilmente far pensare. In realtà, ci aveva già pensato Giulio Verne nel 1870 nel suo celebre romanzo "Dalla Terra alla Luna". Beh… il modo usato da Verne per arrivare sulla Luna era del tutto simile a quello dello sparo di un proiettile mediante un cannone. Un impulso iniziale e via… fino alla Luna. Le cose sono nettamente meno semplici, ma vengono affrontate proprio in quegli anni da Konstantin Tsiolkovsky (1857-1935), un matematico russo che insegnava a Kaluga, a 150 km da Mosca. Egli fu il primo scienziato al mondo che si interessò al moto nello spazio e pose le basi per le future missioni.
Nel 1896 iniziò la scrittura del manoscritto: “Exploration of the Universe with Reaction Machines” che venne pubblicato nel 1903. Già a quei tempi lui simulava un motore che utilizzasse ossigeno e idrogeno liquidi. L'equazione del moto finale è di estrema semplicità e porta il suo nome. Tuttavia, pensiamo che in piena era spaziale bisognerebbe ricordare molto di più il lavoro fondamentale di questo poco conosciuto insegnante. Ancora oggi tutto si basa sul suo lavoro veramente geniale per i suoi tempi. Ricordiamo che, pochi anni dopo, aveva perfino descritto razzi a stadi multipli e con l’utilizzo di altri propellenti, tra cui perfino il radio e la sua disintegrazione.
Per essere completamente onesti, bisogna dire che, per via del tutto indipendente, l’equazione del moto a massa variabile era già stata formulata nel 1813 dall’inglese William Moore e nel 1873 dal belga Coquillart. Tuttavia, solo Tsiolkovsky intuì il suo utilizzo per i viaggi spaziali e può, perciò, essere considerato a tutti gli effetti il padre dell’astronautica.
Vi sono vari modi per ricavare la formula finale, ma noi useremo quello più semplice, applicabile nel caso teorico di un valore nullo delle forze esterne (compresa la gravità). Una semplificazione che cambia poco, però, il risultato finale e che ancora stupisce per la facilità e il rigore. Annullando le forze esterne, il tutto si riduce alla legge della conservazione della quantità di moto. Una trattazione che potrebbe benissimo essere data come esercizio di meccanica classica (chi vuole può anche provare… senza andare a cercare nel web).
Prima di iniziare pensiamo solo brevemente alla seconda legge della meccanica di Newton. Essa dice:
F = ma = m dv/dt = dq/dt
In pratica ci dice che F è la forza in grado di far cambiare la quantità di moto q di un sistema. Tutto ciò, però se la massa m è costante. Nel nostro caso ciò non è vero, e quindi la variazione della quantità di moto va calcolata con particolare attenzione.
Assumendo che non vi siano forze esterne F, la relazione precedente dice anche che dq = 0, ossia che q deve essere costante (conservazione della quantità di moto). Il tutto, perciò, si riduce ad annullare la variazione della quantità di moto totale del sistema, ossia mantenere costante q del sistema razzo più combustibile.
La relazione che troveremo ci dirà che un corpo può accelerare, semplicemente espellendo parte della sua massa in senso opposto a quello in cui si vuole che aumenti la sua velocità. Sembra una cosa ovvia, oggi giorno, ma è stata veramente un’idea rivoluzionaria. Ciò che si doveva fare era solo riuscire a espellere materiale (gas di scarico) a grande velocità e sfruttare questo fenomeno come SPINTA per il razzo vero e proprio. Il combustibile serviva, in pratica, sia come massa da eliminare gradatamente sia come mezzo per espellere tale massa.
L’equazione finale si può ricavare sia nel sistema di riferimento dell’osservatore in quiete, sia nel sistema di riferimento del razzo. Noi, useremo la seconda strada, più semplice, che niente cambia nel risultato finale che ci deve fornire solo una variazione di velocità del razzo. Questo approccio è usato molto poco in letteratura, ma posso assicuravi che nulla cambia nell’equazione finale. Quello che conta, infatti, è che il razzo riesca ad aumentare la propria velocità e poco importa rispetto a quale sistema di riferimento lo faccia.
La Fig. 1 ci mostra il razzo in volo.
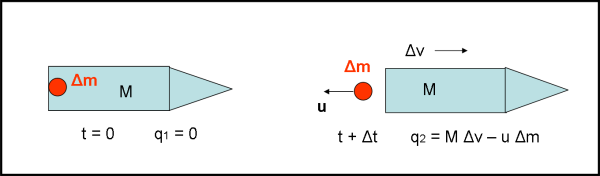
La sua massa sia M + Δm, dove Δm è la massa di carburante che sta per essere espulso Nel suo sistema di riferimento il razzo può considerarsi fermo all’istante t = 0. Ciò vuole solo dire che la sua quantità di moto iniziale q1 può essere considerato uguale a zero:
q1 = (M + Δm) v = 0
Al momento t + Δt il sistema razzo si divide in due parti: il razzo di massa M e la massa di gas di scarico Δm che si allontana verso sinistra con una velocità – u (rispetto al razzo vero e proprio) considerata costante. Ovviamente, è necessario tener conto che la quantità di moto è cambiata e può essere scritta come somma tra quella della massa espulsa e quella del razzo che ha adesso una massa M e una certa velocità Δv:
q2 = M dv – u Δm
La quantità di moto deve conservarsi, dato che non agiscono forze esterne, e quindi otteniamo:
q1 = q2 = 0
M dv – u Δm = 0
Detto fatto! Questa è in pratica l’equazione del moto del razzo…
Basta ora passare a valori infinitesimi e si ottiene l’equazione differenziale:
M dv – u dm = 0 .... (1)
Dividendo tutto per dt si ha la legge del moto da paragonare alla seconda legge della dinamica:
F = Mdv/dt – u dm/dt
Dove, però, F = 0 e quindi:
M dv/dt = u dm/dt .... (2)
La spinta necessaria ad accelerare la massa M è data proprio dalla velocità di espulsione e dalla massa espulsa.
Torniamo all’equazione (1) e facciamo una giusta considerazione (tornare alla (1) vuole anche dire moltiplicare per dt la (2)): Il secondo membro è legato alla massa espulsa e non alla massa del razzo che diminuisce. In altre parole, è molto meglio sostituire l’aumento di gas espulso con la diminuzione di massa del razzo. Beh… molto facile, basta cambiare di segno è sostituire dm con dM. La (1) diventa:
M dv = - u dM
dv = - u dM/M
Basta ora integrare entrambi i membri per avere la relazione tra velocità finale e massa del razzo iniziale e finale:
ʃ0 vf dv = - u ʃMin Mfin dM/M
Ricordiamo che l’integrale di 1/M non è altri che il logaritmo naturale di M (o –se preferite- la derivata del logaritmo naturale di M vale proprio 1/M)
vf - 0 = - u (ln Mfin – ln Min) = u (ln Min – ln Mfin)
vf = u ln (Min/Mfin) .... (2)
la velocità u è costante e ne segue che al diminuire della massa del razzo (Min > Mfin) la velocità del razzo cresce.
Vogliamo rendere la faccenda più “pratica” ancora? possiamo tornare all’equazione (2) e interpretarla come l’accelerazione del razzo.
a = u (dm/dt)/M
esplicitiamo meglio la M. Essa è composta dalla massa del razzo vuoto (Mvu) più la massa del carburante iniziale (Mc) (Mvu + Mc è la massa del razzo pieno, alla partenza), da cui è stata espulsa una certa quantità di massa di ga di scarico (Me).
a = u (dm/dt)/(Mvu +Mc - Me)
Come possiamo esprimere ciò che viene scritto da questa apparentemente “arida” formula? Bene possiamo dire che l'accelerazione del razzo è variabile in quanto il denominatore del secondo membro è funzione del tempo. Man mano che passa il tempo, infatti, la massa di materia espulsa aumenta e quindi il denominatore diminuisce, fino all'esaurimento totale del combustibile (Mc = Me). L'accelerazione dipende anche dalla velocità di espulsione dei frammenti u, che può essere immaginata dipendere dal tipo di motore montato sul razzo. L'accelerazione, però, dipende anche da dm/dt che e' il ritmo con cui il gas di scarico viene espulso. Questo termine non è altro che ... l'acceleratore di un'autovettura. Ovviamente, quando finisce la benzina (M = Mvu), l'auto deve fermarsi (dm/dt = 0). Tutto semplice e banale… sapere interpretare una formula matematica può aprire gli occhi sulla realtà che ci circonda… basta saper leggere tra le righe, o -meglio- tra i simboli.
Teoricamente, se il razzo fosse leggerissimo, si otterrebbe una velocità quasi infinita. Come sempre, tutto funziona sempre che si resti su valori della velocità ben lontani da quelli della luce. Altrimenti è necessario tenere in conto la relatività …
Non sarebbe nemmeno troppo complicato scrivere l’equazione relativistica, ma dovremmo prima introdurre qualche funzione che ancora non conosciamo (seno, coseno e tangente iperbolici). Pensiamoci sopra… e, per adesso, accontentiamoci. Un giorno, chissà...
QUI riproponiamo l'equazione del razzo (degna di nota l'appendice semplificata)






7 commenti
Quindi più velocemente vengono espulsi i gas di scarico e maggiore è la velocità del razzo per l'effetto azione-reazione. Mi confermi che grande importanza ha a tale scopo la forma dell'ugello capace, se ricordo bene, di accelerare i gas da velocità subsoniche a supersoniche attraverso la sua forma dapprima convergente e poi convergente.
Sono ricordi quasi di infanzia (10-11 anni), quando nel dopoguerra disponevamo di grandi quantità di proiettili di tutti i tipi abbandonati dai tedeschi in fuga. Li aprivamo e con la balestite che contenevano provavamo a costruire razzi sempre più sofisticati. L'ugello lo sagomavamo bucando il tappo (di legno o di ferro) che mettevamo sul fondo del tubo. Se ben ricordo aveva una gola di circa un terzo del diamero del tubo. Se era troppo stretto il razzo esplodeva, se era troppo largo bruciava tutto il propellente senza muoversi dalla base di lancio.
Allora studiavo con avidità la benemerita rivista "Scienza e Vita" che dedicava alla missilistica una apposita rubrica. Erano anni entusiamanti, con la feroce gara tra Unione Sovietica e Stati Uniti per la "conquista dello spazio" e lo Sputnik non era un triste vaccino...
Non sono un tecnico, caro Alberto, ma sicuramente conta tutto ciò che riesce ad aumentare la velocità di espulsione... intesa come quantità di massa che si riesce a espellere in un certo tempo.
Mi sa questo articolo me lo ero perso, sempre interessante scoprire articoli "persi". Thanks Alberto.
Ma la curiostà è inarrestabile Enzo.....Come diventa la formula se consideriamo la gravità e vogliamo trovare la massima velocità di fuga possibile con gli attuali carburanti chimici immaginando di avere un pianeta sempre più massivo da cui fuggire? Penso che esista un punto in cui il peso del carburante necessario sia oltre la spinta dell'energia ricavabile dalla reazione anche solo per staccarsi dal suolo. I punti di equilibrio dovrebbero essere due, uno in funzione della densita e uno in funzione del raggio, considerando pianeti non gassosi. O sbaglio?
caro Frank,
io direi che tutto dipende dalla velocità u, che ha già in se stessa il problema della gravità. Se si raggiunge una certa u, poi tutto funziona come nell'articolo... Ma poi chi è l'esperto "pratico". Dovresti essere proprio tu a complicare (e risolvere) la faccenda. La u dovrebbe essere espressa come impulso specifico moltiplicato per la gravità g. La butto un po' così... ma dovrebbe essere giusto...
Frank... vedi un po' se la trattazione dell'impulso specifico ti soddisfa... io ho problemi di ... cinghiale...
https://en.wikipedia.org/wiki/Specific_impulse
In che senso? Lo stai cucinando? No no ho capito vista l'ora sicuramente te ne sarai ingozzato e adesso fai il coccodrillo......
Tranquillo non ho intenzione di trasferirmi su Kepler 10c. Comunque leggo al link indicato, si sa mai che cambio idea.
ma che dici? Vista l'ora è proprio perché lo sto cucinando. Ormai dovrebbe essere pronto...