Dopo aver giocato a golf tra mamba e arbitri molto parziali, dedichiamoci a un gioco meno “pericoloso”: il tennis. Ma sarà proprio così? Questo articolo scritto a due teste e quattro mani (quelle di Maurizio e quelle di Vincenzo) nasce da un'idea paranoica di Pautasso in onore del suo grande amico Fantozzi. Chi vuol provare ha tutti i dati a sua disposizione.

Oggi abbiamo deciso di abbandonare il golf (troppo complicato) e abbiamo deciso di dedicarci al tennis. Tuttavia, così come accadde a Fantozzi e Filini nel loro epico incontro, vi è un nebbione terribile.

Il guaio è che il nostro avversario non si è presentato o è sparito nell’oscurità… Non ci resta che una soluzione: giocare da soli.

Bene, chiunque lo può fare!

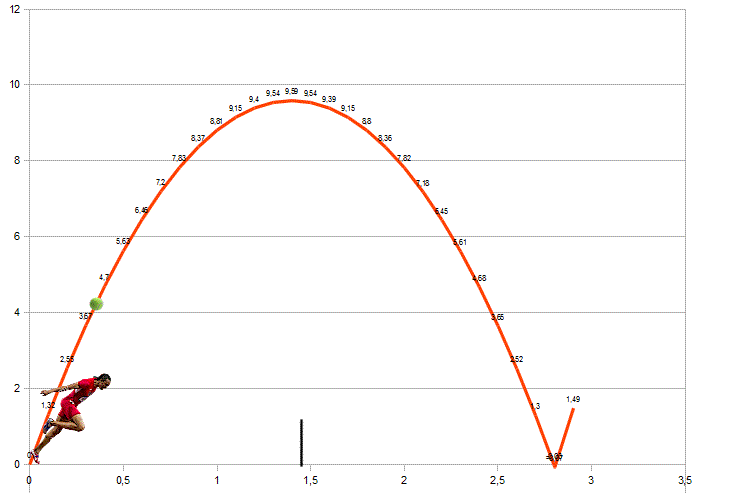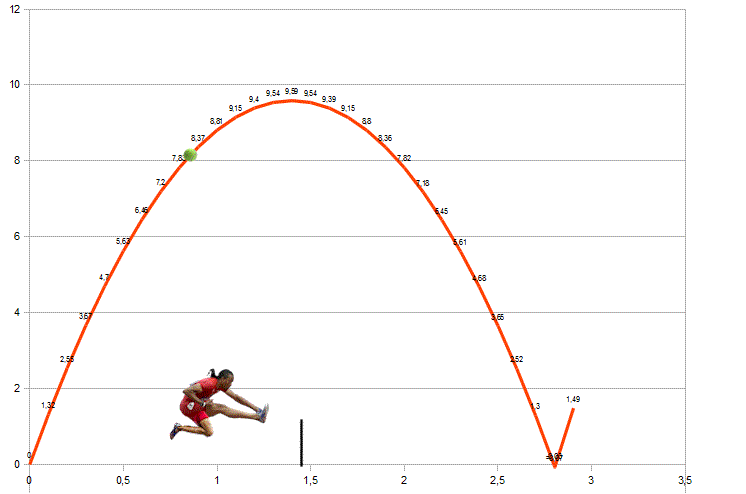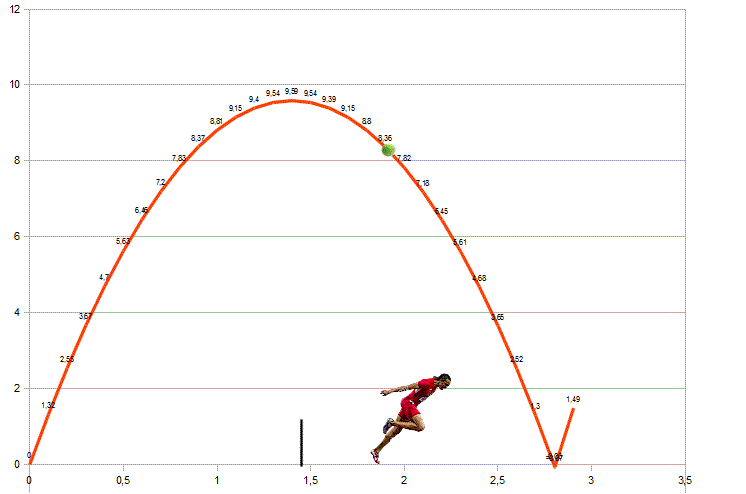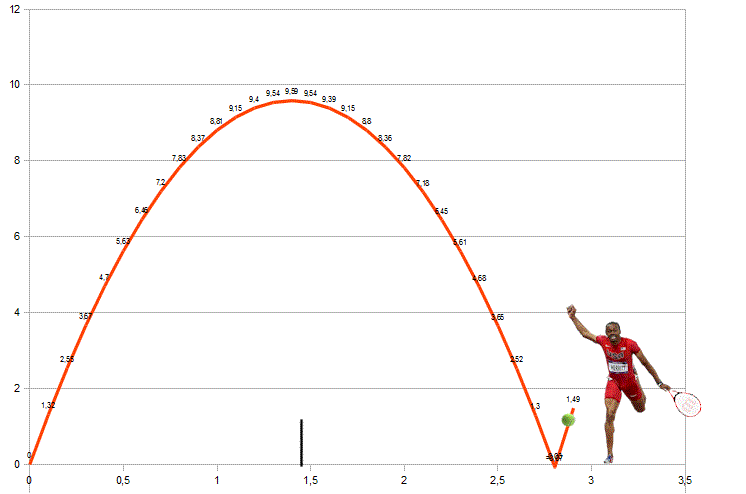
Il problema è tirare la pallina e poi correre, saltando la rete (aggirarla sarebbe impresa troppo difficile), e arrivare al fondo campo avversario in tempo per rilanciare la pallina. Avendo le forze e ragionando in termini teorici… la partita potrebbe continuare!

Vedremo che perfino Fantozzi lo potrebbe fare, dato che ognuno ha solo bisogno di un lancio adatto alle sue possibilità atletiche.

Il dato fisso e intoccabile è la lunghezza del campo D

Noi riusciamo a correre da un capo all’altro del campo in un certo tempo T che dipende dalle nostre capacita fisiche. Ovviamente bisogna scavalcare la rete in qualche modo, ma la sua altezza è soltanto 90 cm.

Data la distanza D (gittata del lancio parabolico) e il tempo di volo T (variabile) è possibile determinare il tipo di lancio da fare, ossia determinare, per ogni tempo T, l’alzo del tiro α e la velocità v da imprimere alla pallina.

Non riportiamo tutto il calcolo della traiettoria parabolica, ma potete consultare questo articolo, oltre a curiosare nella sezione “Dinamica e Meccanica”  del blog. Chi  avesse la fortuna di avere in casa questo libro, non avrà che andarsi a rileggere il capitolo sul moto parabolico, precisamente il capitolo 11, intitolato: "Puntate...mirate...fuoco !)”

Riportiamo solo le formule fondamentali che ci saranno utili (g è l’accelerazione di gravità e vale 9,81 m/s²):

Gittata

D = 2 v_x v_y/g = 2 v sin(α) v cos(α)/g     …. (1)

Tempo di volo

T = 2 vy/g = 2v sin(α)/g                   …. (2)

La Fig. 1 illustra il significato dei vari parametri.

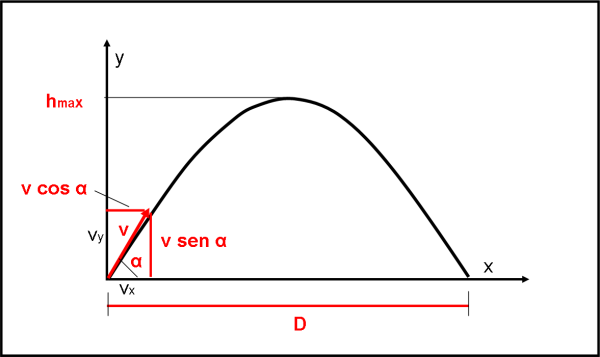
Dalle due relazioni precedenti possiamo esprimere le due componenti della velocità v  lungo x  e lungo y in funzione dei dati  D e T che caratterizzano la parabola

Inserendo la (2) nella (1) ricaviamo v cos(α), la componente orizzontale della velocità

D = T v cos(α)

v cos(α) = D/T             …. (3)

La (2)  permette di ricavare v sen(α) , la componente verticale della velocità

v sen(α) = Tg/2            …. (4)

quadrando e sommando la (3) e la (4) si ha:

v²cos²(α) + v²sen²(α) = D²/T² + T²g²/4

v² = D²/T² + T²g²/4          …. (5)

Questa relazione ci permette di calcolare la velocità del lancio per ogni tempo T scelto. La curva è una iperbole come si può vedere subito ponendo v² = y e T² = x

y = D²/x + xg²/4

y = (4D² + x²g²)/4x

x²g² - 4xy + 4D² = 0

Questa è una conica dato che è una funzione del tipo:

ax² + 2bxy + cy² + 2dx + 2ey + f = 0

Nella nostra curva abbiamo:

a = g²

b = - 2

f = 4D²

c = d = e = 0

se

b² – ac  > 0      siamo nel caso dell’iperbole

Noi abbiamo:

(-2)² – g²·0 = 4 > 0

Si potrebbe tranquillamente studiare questa funzione, ma per il nostro scopo basta tracciarla nella forma (5), estraendo la radice quadrata di entrambi i membri:

v = (D²/T² + T²g²/4)^1/2

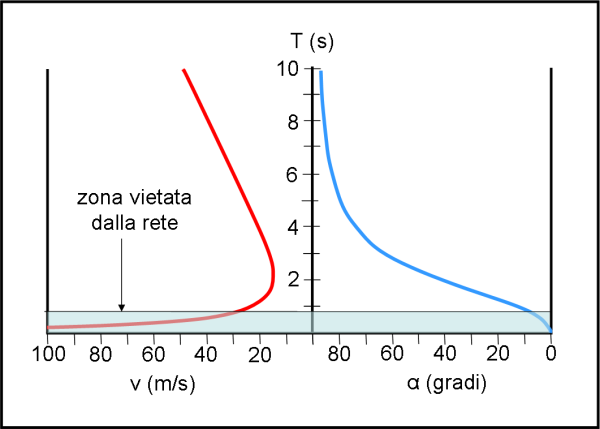
Ponendo D = 23 m e g = 9.81 m/s², il grafico di Fig. 2, ci mostra come varia la velocità del lancio per i diversi tempi che siamo capaci a raggiungere.

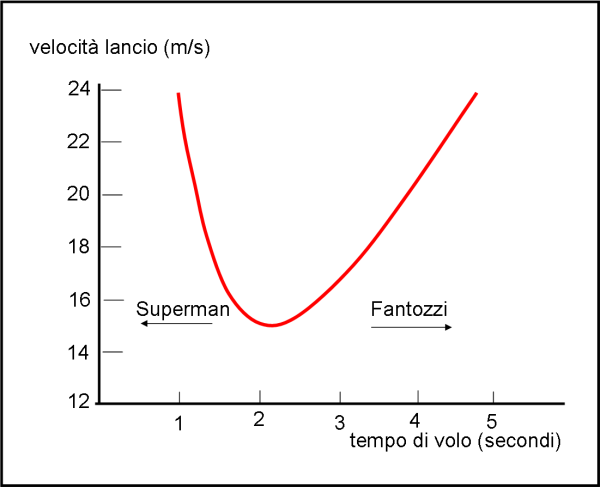
Si nota molto bene che la velocità raggiunge un minimo che separa i superman dalle persone normali. A destra del minimo possiamo andare sempre più piano, tenendo conto che dobbiamo aumentare la velocità del lancio e l'alzo, in modo da avere parabole più alte (a campanile),con velocità orizzontale più bassa. Ricordiamoci, infatti, che il tempo di volo dipende solo dalla componente orizzontale della velocità.

Per valori del tempo di volo sempre più corti, la velocità aumenta nuovamente, ma l'alzo è decisamente più basso.

In parole povere, la differenza sostanziale tra le due parti dell'iperbole è l’angolo di alzo della parabola: a parità di velocità della pallina si può avere un tiro con alzo molto basso (adatto ai superman), oppure con alzo sempre più grande (adatto ai Fantozzi).

A questo punto è necessario, perciò, collegare la velocità all’alzo attraverso il tempo T .

Per trovare una relazione tra l’angolo α e il tempo T, un modo molto rapido è di considerare nuovamente le relazioni  (4) e (3) e farne il rapporto:

v sen(α) = Tg/2

v cos (α) = D/T

v sen(α)/v cos(α) = (Tg/2)/(D/T) = T²g/2D

tan(α) = T²g/2D

α = atan(T²g/2D)

Ponendo g = 9.81 m/s² e D = 23 m

Si ottiene il grafico di Fig. 3 che lega l’alzo α con il tempo T.

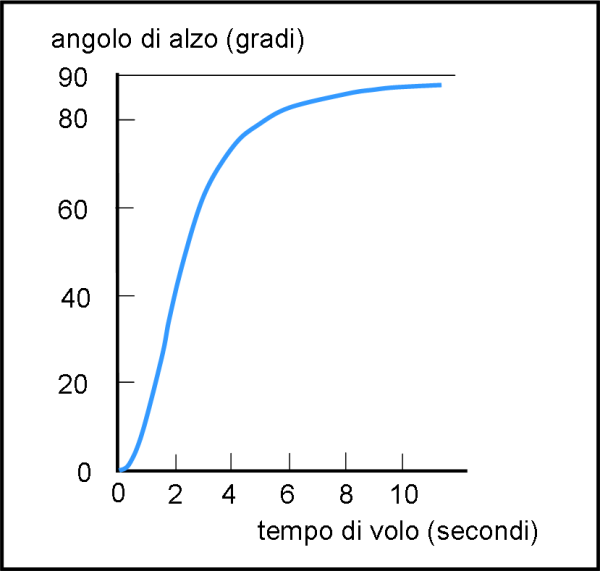
Mettendo uno a fianco dell’altro i due grafici, si calcolano immediatamente i valori dell’alzo e della velocità per ogni tempo T necessario al giocatore solitario sceso in campo, come riportato in Fig. 4 (inserendo il tempo come ordinata).

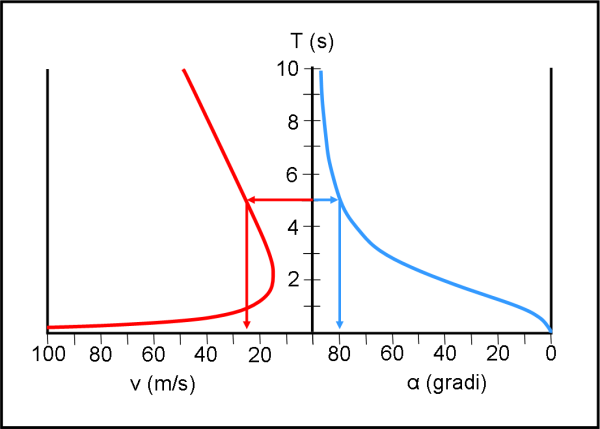
Tracciando delle rette con velocità costante nel grafico dell’iperbole si ottengono due valori del tempo. Questo implica che esistono sempre due  parabole con alzi diversi che permettono di raggiungere la stessa distanza (gittata della parabola).  Con i due valori di T si trovano subito questi due angoli nel grafico dell’arcotangente. Ma c‘è davvero bisogno di cercarli entrambi? Assolutamente no! Basta usare la (1)

D = 2 v_x v_y/g = 2 v sin(α) v cos(α)/g

Data una certa velocità v, si ottiene la stessa distanza D sia con l’angolo α che con l’angolo 90 – α. Infatti sappiamo benissimo (QUI) che sin(90 – α) = cos(α) e che cos(90 – α) = sen(α). L’espressione rimane la stessa.

cos(90-a) sin(90- a)  = sin(a) cos(a)

Ne segue che le due soluzioni sono sempre angoli complementari! In poche parole, otteniamo due parabole con pari velocità, ma con alzi di α e 90 –α. Ovviamente cambiano i tempi di volo. Una parabola, quella con angolo piccolo, è alla portata dei superman; quella con angolo più alto è alla portata di un Fantozzi qualsiasi.

Questo vale in tutti i casi, tranne che nel caso della velocità relativa al minimo dell’iperbole. Vi è un solo tempo e di conseguenza un solo angolo. L’unico angolo tale che α= 90 – α può essere solo α = 45°. Per quel dato tempo (e per quella data velocità) esiste un solo tiro possibile per percorrere tutto il campo ed è quello con un alzo di 45°. Questo angolo pone un limite tra i ... brocchi e i superman.

Domanda: esiste qualcuno che si avvicina più di tutti a questo valore limite (e forse lo raggiunge anche)?

Qualche esempio...

velocità m/s	tempo sui 100 piani (s)	tempo sui 110H (s)	tempo sui 23 m	Chi è
2,9*10^8	34,5*10^-8	34,5*10^-8	0,86 (limite rete)	Flash Gordon – Superman   Kripton
10,43	9,58		2,2	Usain Bolt     (Lightning Bolt ) JA
9,53	10,49		2,41	Florence Griffit                       USA
8,59		12,8	2,68	Aries Merrit                             USA
<    1,38	72,46	Non disp.	16,7	Rag. Ugo Fantozzi                    IT

Aries Merrit, campione del mondo dei 110H è forse il più vicino al limite dei super eroi, sapendo bene come saltare gli ostacoli. Non solo, però... Nei 110H vi sono 10 ostacoli, mentre nei 23 del campo ve ne è solo uno. Potrebbe darsi che il suo 2.68 (relativo ai 110 H) si riduca un po'. Basta chiedergli di fare la prova!

Nella tabella precedente è stato segnato in rosso il valore 0.86 come tempo limite per i supereroi. Un valore molto alto per loro... ma, allora, cosa frena la incredibile velocità dei supereroi?  Il semplice fatto che su lanci troppo bassi la rete intercetta la pallina.

Per eliminare i lanci che finiscono in rete (relativi solo  ai superman) basta considerare la formula che ci dà la massima altezza della parabola:

h_max = ½ v² sen²(α)/g

h_rete  = 0.91

E’ necessario che h_max del tiro sia maggiore dell’altezza della rete, ossia

v²sin² (α)> 2 · 0.91 · g

v sen(α) > (2 · 0.91 · 9.81)^1/2 = 4.225

ma

v sen(α) = gT/2

gT/2 > 4.225

T > 2 · 4.225/9.81 = 0.86

Non sono ammessi tempi minori di 0.86 secondi, dato che implicherebbero l’urto contro la rete. Questo tempo limita  l’alzo verso il basso e, automaticamente, anche la velocità. Nella Fig. 5 vediamo qualche parabola ammessa e quella limite a causa della rete.

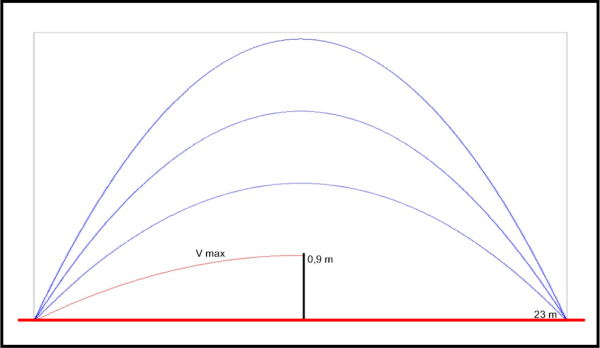
La Fig. 6 ripete la Fig. 4, inserendo la zona inibita  inibita dalla rete. Ossia, quella relativa a tempi di volo minori di 0.86 m/s).

Per essere veramente precisi (ma ne vale la pena?) bisognerebbe tener conto che il giocatore deve arrivare in fondo al campo avversario, potersi girare e respingere la pallina. Ciò vorrebbe dire una velocità leggermente superiore a quella della pallina e/o una gittata leggermente più corta. Ma, a livello Fantozzi va più che bene quanto è stato descritto.

Tenete presente anche il fatto che, più la pallina viene lanciata in alto, per consentire a un giocatore lento di arrivare a fondo campo, più velocemente arriverà a terra, ricadendo. Giusto per darvi una idea, pensate che il mitico Ragioniere, "correndo" a 1,38 m/s  avrà bisogno di tenere in volo la palla per  16,7 secondi. Di conseguenza dovrà batterla  con un alzo  a= 89°  e con velocità V=  79 m/s .

Quando la palla ricadrà dalla massima altezza raggiunta      =  318 metri  ( 18 m più della torre Eiffel),   gli piomberà addosso alla velocità    = 79 m/s, ossia , inevitabilmente, la stessa velocità della battuta. E la velocità di  79 m/s significa ben 274 Km/h.  Il tennis  in solitario ha i suoi rischi.

Bene, non possiamo che augurarvi una buona partita, sperando che vi siate divertiti imparando qualcosa sul moto parabolico!