Questo articolo è stato inserito nella pagina d'archivio "La caduta libera" compresa nelle sezioni "Dinamica e meccanica" e "Relatività Generale"

 

In questo articolo presentiamo tre classici esempi di meccanica classica che aprono le porte a una delle idee base della relatività generale. Lo facciamo attraverso domande all'apparenza abbastanza banali, ma sufficienti a comprendere cosa voglia dire essere in caduta libera.

 

Il bicchiere pieno d'acqua

Per fare divertire i propri figli o nipotini o amici (come volete voi) si può fare una scommessa con loro, che può anche assomigliare a un gioco di prestigio. Prendo un bel bicchierone di carta e  gli faccio un buco A nella parte bassa. Poi tappo il buco con il pollice e chiedo agli ascoltatori cosa succederà all’acqua contenuta nel bicchiere. Tutti diranno: “Esce dal buco”. Tolgo il pollice e, effettivamente, l’acqua esce dal buco in pochi secondi o anche meno.

Rimetto il pollice sul foro, lo riempio di nuovo di acqua e faccio una scommessa con gli spettatori: “Scommettiamo che riesco a togliere il pollice e a  non far cadere nemmeno una goccia d’acqua dal foro, per un periodo di tempo uguale a quello di prima?”

Tutti si mettono a ridere, ma io vinco la scommessa… Come ho fatto?

Ovviamente, non posso usare tappi o altre cose del genere  e, nemmeno, immergere il bicchiere nell’acqua.

Un bicchiere posato sul tavolo o trattenuto in mano sente una forza contrapporsi alla sua voglia di cadere sotto il dominio della legge di gravità (il tavolo stesso o i muscoli del braccio). Se vi è un buco, l’acqua del bicchiere è, invece, soggetta liberamente alla forza di gravità e tende quindi a uscire dal buco per obbedire ai dettami di Newton. Ci troviamo di fronte a una situazione contrapposta: qualcosa è trattenuto e qualcosa no. Si potrebbe, perciò, esercitare una forza anche sull’acqua per non farla cadere, ossia unaforza che si opponga a quella di gravità. Ad esempio un tappo o anche il solo pollice.

Tuttavia, vi è un’altra soluzione: fare in modo che sia l’acqua che il bicchiere subiscano entrambi la forza di gravità, senza alcun intoppo. Sappiamo benissimo che la velocità di caduta dei corpi verso terra NON dipende dalla loro massa. Già questa conclusione ci porta verso un “principio di equivalenza”: la massa inerziale che si oppone alla caduta deve essere uguale alla massa gravitazionale su cui agisce la forza di gravità. Un’equivalenza già nota a Galileo… e verificata dagli astronauti sulla Luna!

In altre parole, dobbiamo lasciare sia l’acqua che il bicchiere in preda della forza di gravità. Entrambi cadono con la stessa velocità e, nel sistema di riferimento solidale con il bicchiere e l’acqua, non vi è alcuna velocità relativa. Essi stanno sicuramente cadendo verso il suolo, se visti da fuori, ma all’interno tutto appare perfettamente fermo. Niente si muove di moto proprio e, quindi acqua e bicchiere restano immobili: l’acqua non può uscire perché non vi è nessuna forza che l’aiuta a far ciò.

In poche parole, abbiamo cambiato sistema di riferimento e ci siamo portati in quello che si chiama “in caduta libera”, dominato solo e soltanto dalla forza di gravità.

Tuttavia, sappiamo bene che chi vive in un sistema non inerziale (e il bicchiere-acqua lo è, dato che sta accelerando), per potersi sentire fermo, ha bisogno di una forza uguale contraria a quella che sta subendo (o ancora meglio accelerazione). E’ lo stesso discorso della forza centrifuga che si oppone alla forza centripeta.

Vi è, insomma, bisogno di una forza apparente, che però è avvertita (e come) da chi si sente fermo. Nella caduta libera questa forza apparente non è altro che una forza uguale e contraria a quella di gravità. Sarebbe addirittura più giusto parlare solo di accelerazioni, dato che la massa non compare, essendo ininfluente. Ciò che è all’interno del bicchiere, dato che viene annullata la gravità, non avverte il suo peso (che è proprio la forza di gravità).

In altre parole: caduta libera = assenza di peso.

Siamo nel caso del celebre ascensore di Einstein, trattato anche dai nostri amici Astericcio & co (QUI e QUI). Ricordiamoci che la stessa cosa capita a chi orbita attorno alla Terra su una navicella. Anch’egli è soggetto alla forza di gravità che viene bilanciata dalla forza centrifuga. Nel suo sistema di riferimento non avverte peso e può considerarsi in caduta libera, in modo del tutto analogo al bicchiere che cade. Smentiamo ancora una volta l'errata idea che sulla Staziona Spaziale non si senta più la gravità terrestre! Anche la Luna la sente (che è ben più lontana), ma gli astronauti sono solo e soltanto in caduta libera e quindi possono volteggiare senza peso.

 

Un soldato  dalla mira molto scarsa

Si prepara una specie di scatola chiusa in cui si inserisce il fucile A. Tracciando una retta perfetta dalla bocca dell’arma da fuoco si arriva a un chiodo B. Per complicare la faccenda e per testare la bravura del soldato e la precisione nella mira, tra il fucile e la parete in cui si trova il chiodo viene inserita una lastra di metallo con un foro F in perfetta corrispondenza della retta AB. Il foro è molto piccolo e permette il passaggio al proiettile solo se la sua traiettoria è perfetta.

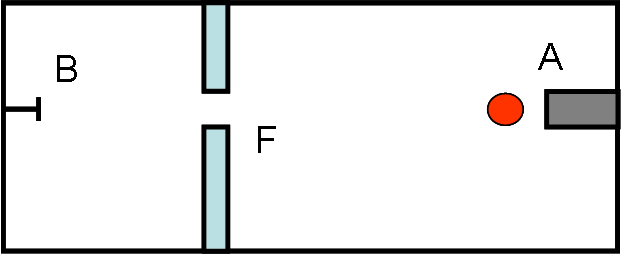Si dà il via all’esercitazione e… che pena! Dopo dieci tentativi, il soldato non è riuscito a fare un centro: tutti in proiettili sono finiti contro la parete di metallo e sono rimbalzati indietro.

(1) E’ veramente colpa della sua mira? (2) Cosa bisognerebbe fare affinché il soldato riesca a colpire  il chiodo B ?

Come vi dicevo non c’è bisogno di tante formule, anzi solo un po’ di ragionamento e ricordare il bicchiere pieno d’acqua…

Povero soldato, la colpa non è sua. Il fucile, i fori e il chiodo-bersaglio sono immobili perché trattenuti dal terreno che si oppone alla loro caduta. L’unica cosa che può muoversi è il proiettile. Come lui esce dalla bocca del fucile, ha una certa velocità rettilinea e uniforme, ma, purtroppo, non è trattenuto da niente e quindi subisce anche un’accelerazione di gravità che lo spinge verso il basso. La sua velocità uniforme è continuamente disturbata da una velocità crescente dovuta all’azione di quella di gravità. Ne risulta un moto parabolico che tende a portarlo verso il basso. In realtà, tutto ciò dipende dal fatto che il proiettile è in caduta libera (oltre che soggetto a una certa velocità uniforme), mentre fucile, fori e chiodo no.

Basta allora lasciare che tutto sia in caduta libera, eliminando il pavimento (Fig 1a).

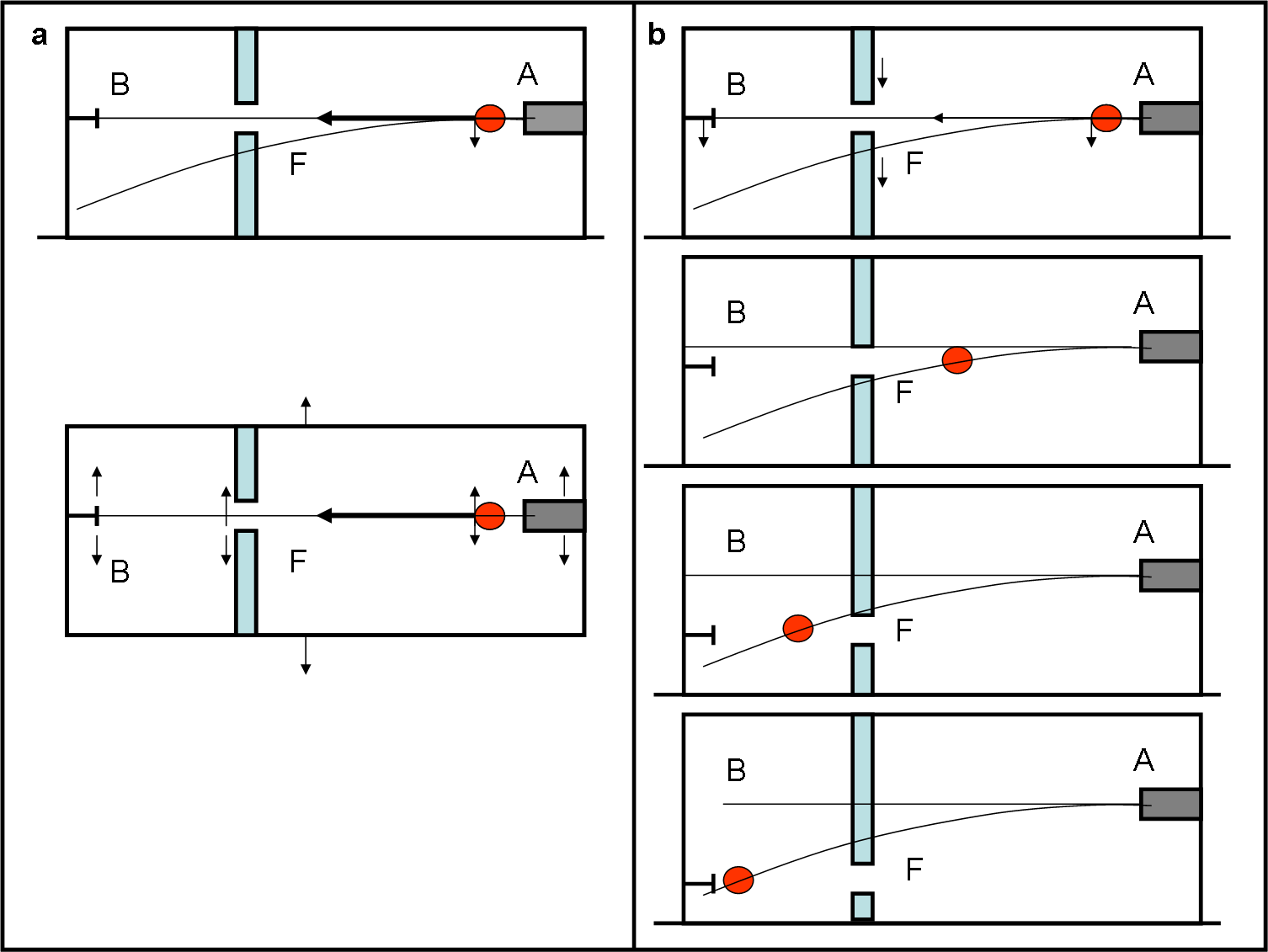
A questo punto, parete di metallo con il suo foro, fucile e bersaglio subiscono tutti la stessa gravità del proiettile. L’intera scatola è in caduta libera e gli oggetti sono senza peso (bilanciato dalla solita forza apparente uguale e contraria – attenzione, non siamo nel terzo principio della dinamica! Lo abbiamo spiegato QUI).

Essi sono, quindi, completamente fermi e lo sarebbe anche il proiettile se non avesse un moto rettilineo uniforme impartitogli dal fucile. In questo sistema immobile, il proiettile si muove solo lungo una retta e non ha alcun problema a passare nel foro e colpire il chiodo.

L’intera faccenda è completamente equivalente a quella del bicchiere d’acqua. Vi è stata solo l’aggiunta di un moto a velocità costante e rettilineo all’interno del sistema in caduta libera.

Cosa dovrebbe succedere al soldato per vedere il suo proiettile attraversare il foro e colpire il chiodo, pur restando con i piedi per terra? Piuttosto facile, teoricamente (Fig. 1b). Al momento dello sparo, sia il foro che il chiodo dovrebbero scendere sotto l’effetto della stessa accelerazione di gravità del proiettile. In qualche modo, bisognerebbe applicare un movimento alla parete e al chiodo, che simuli perfettamente quello dovuto alla gravità. In questo modo il proiettile potrebbe tranquillamente seguire la sua parabola e saprebbe di incontrare il foro al posto giusto così come il chiodo.

Praticamente, basterebbe trattenere in qualche modo la parete col foro e la parete col chiodo, prima dello sparo, e poi lasciarle libere di cadere al momento esatto dello sparo. Facendo così, avremmo costruito un sistema in caduta libera (proiettile-foro-chiodo) che manterrebbe l’immobilità reciproca degli oggetti, a parte il moto rettilineo orizzontale uniforme del proiettile. In questo sistema, basta mirare al foro (e al chiodo) per essere sicuri del risultato finale.

 

La  furba scimmietta

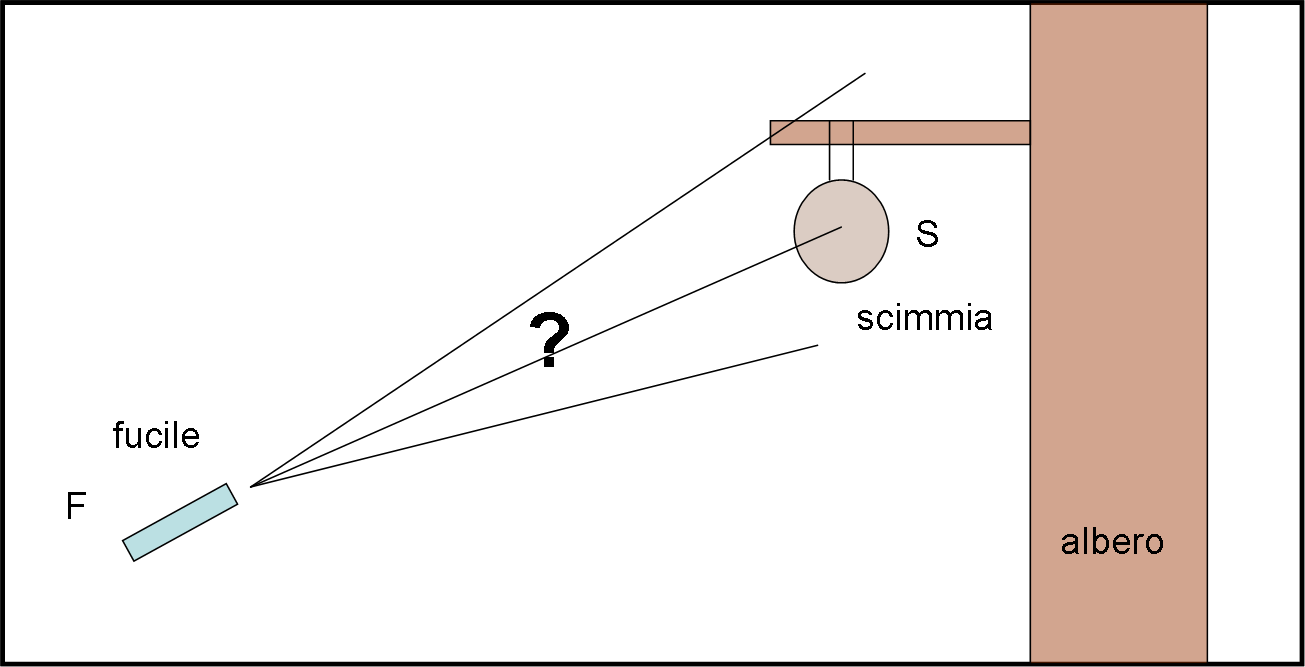
Un esploratore vuole catturare una scimmia di una razza molto rara e particolarmente intelligente (per poi liberarla dopo vari controlli sulla sua salute).

Non è facile e quindi sceglie di sparagli  un proiettile che l’addormenti soltanto. Si munisce di un fucile F ad alta precisione e si incammina nella foresta. Finalmente, ecco un bell’esemplare S, appeso a un ramo di un albero molto alto.

L’esploratore si nasconde e inserisce un piccolo marchingegno che faccia vedere un lampo notevole, al momento esatto dello sparo (fuoriuscita del proiettile). Adesso è questione di prendere la mira… Conoscendo la furbizia di quelle scimmie, è SICURO che l’animale, appena visto il lampo, si lascerà cadere dal ramo.

Dove dovrà sparare l’esploratore per essere SICURO di colpire la scimmietta? Sopra la posizione attuale, sotto o esattamente nella direzione attualmente occupata dalla scimmia?

(1) Descrivere il tutto per via cinematica e (2) dimostrare che qualsiasi sia la velocità del proiettile (sempre che riesca ad arrivare fino all’albero, ovviamente) la scimmia non ha scampo e viene colpita e catturata.

Il sistema esploratore-fucile-proiettile-scimmia è del tutto analogo e ancora più semplice del problema precedente, dato che non vi è nessuna parete con un foro a rompere le scatole al proiettile.

L’esploratore e il fucile possono pure restare con i piedi per terra. A noi basta che siano in caduta libera il proiettile e la scimmia. Se, al momento dello sparo, la scimmia si lascia cadere, il sistema proiettile-scimmia è in caduta libera e, quindi, l’unico movimento che avviene in questo sistema è quello rettilineo del proiettile, che deve, perciò, essere diretto esattamente verso la scimmia. Poi tutto avviene esattamente come nel caso del soldato e del chiodo (senza il foro).

La scimmia e il proiettile cadono allo stesso modo e si incontreranno sicuramente, prima o dopo, a
seconda della velocità del proiettile. Questo valore conta poco, così come non contava nel caso del
soldato. Il proiettile passa comunque. Così la scimmia viene colpita ad altezze diverse se la velocità
(come modulo) aumenta o diminuisce. Quello che conta è la direzione della velocità : il foro-chiodo nel primo caso, scimmia nel secondo.

Qualcuno potrebbe dire: “E se il fucile F sparasse un proiettile troppo lento e questo cadesse prima di raggiungere l’albero?”. Praticamente, avrebbe ragione, ma non teoricamente. Immaginate di eliminare il terreno e di lasciare proseguire nella loro caduta sia proiettile che scimmia S: Anche se molto più in basso (- h1) l’incontro avverrebbe comunque (Fig. 2)

In poche parole, se se il sistema è in caduta libera, niente può disturbare il moto rettilineo di un proiettile, che vede il bersaglio immobile per tutto il tempo del viaggio.

Non voglio andare oltre in questa trattazione, che ci porterebbe facilmente all’equivalenza di Einstein. Però, vale la pena ricordare che ciò che capita in un sistema in caduta libera per effetto dell’accelerazione di gravità capiterebbe allo stesso modo, se riuscissimo ad andare in uno punto dello Spazio in cui non agisse alcuna gravità. In entrambi i casi saremmo senza peso e non sapremmo dire, vivendo all’interno di questo sistema, se stiamo cadendo verso una tragica fine (ascensore di Einstein) o se siamo realmente immobili rispetto all’infinito che ci circonda.

Bene, direi che dal punto di vista concettuale abbiamo sciolto ogni dubbio (è molto importante ragionare in questo modo per avvicinarci al  ragionamento di Einstein). Tuttavia, il problema è ben lungi dall’essere relativistico e possiamo risolverlo attraverso la più semplice cinematica newtoniana, attraverso poche e semplici formule.

Abbiamo scelto un metodo che non faccia uso di trigonometria, ma le vie che si possono seguire sono diverse, pur dicendo la stessa identica cosa.

Per far ciò basta partire dal “fondo”, ossia scegliere una soluzione tra le tre proposte e dimostrare
che è quella giusta. In tal modo, i passaggi risultano semplificati e il punto chiave che lega questo
problema a quello del bicchiere e del fucile e il chiodo risulta più evidente.
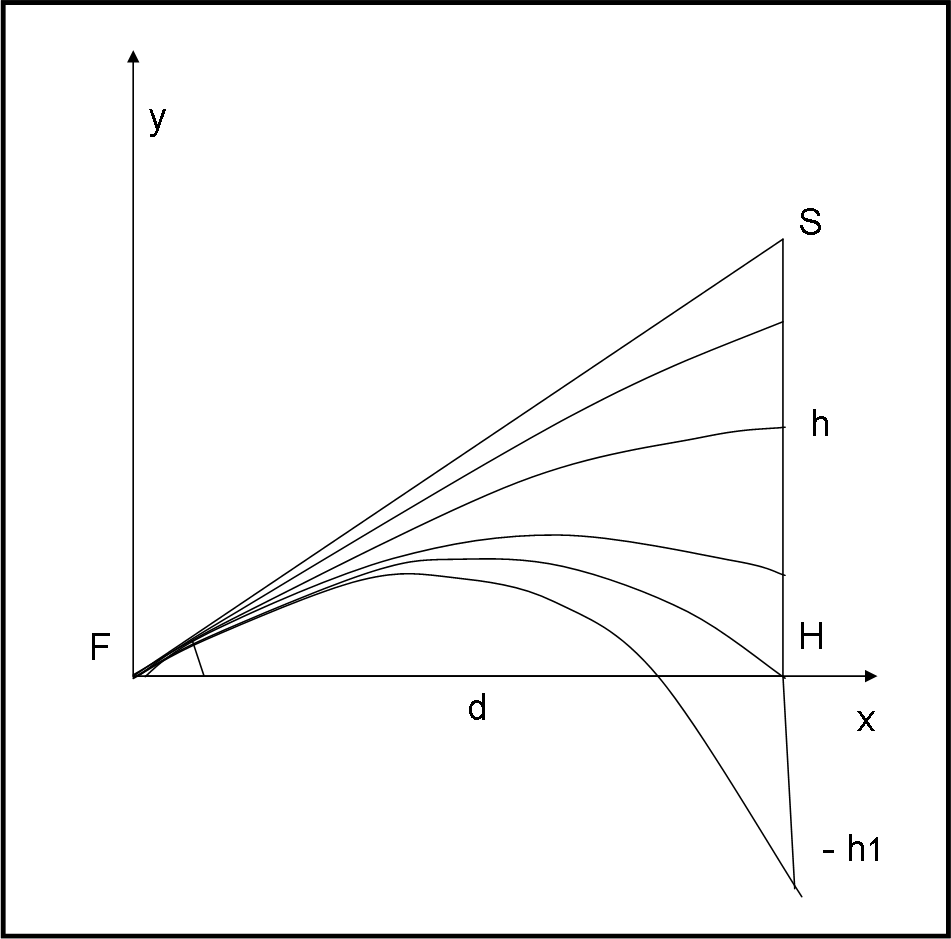
Facciamo in Fig. 3, un disegno estremamente schematizzato della situazione.

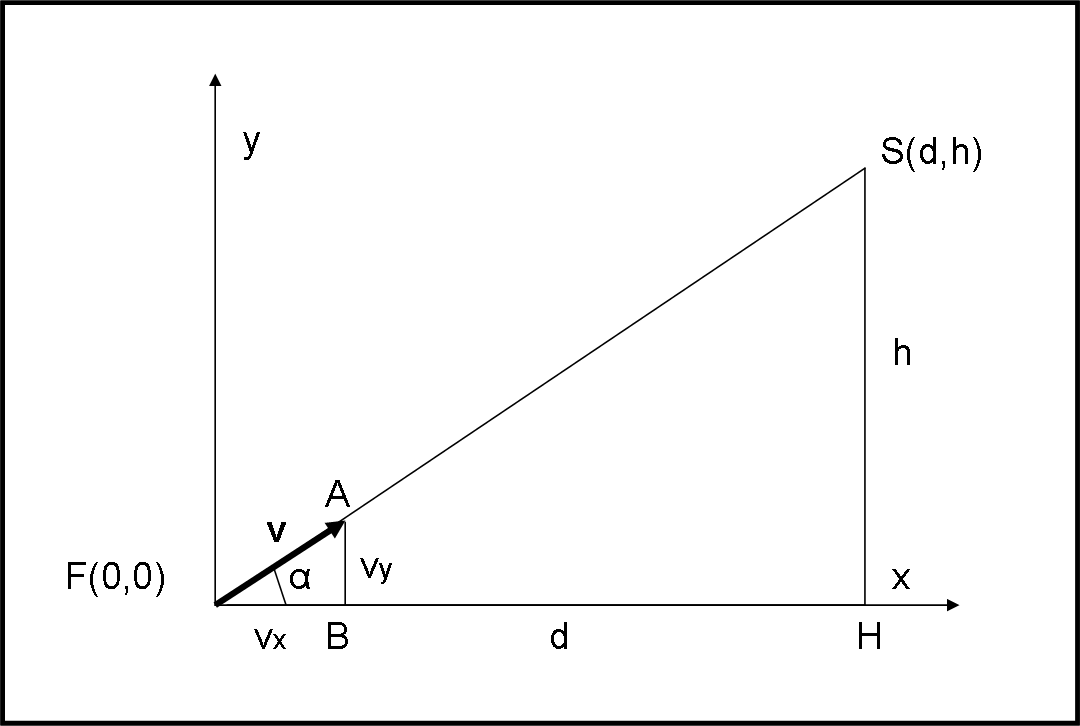
La scimmia si trova in S a una distanza d dall’esploratore F e a un’altezza h. Il cacciatore (o meglio la bocca del suo fucile) è invece posto nell’origine degli assi. Il tempo si misura a partire dal momento dello sparo che coincide con la caduta della scimmia. Consideriamo del tutto trascurabile il tempo che la pallottola impiega ad andare dal fucile alla scimmia.

Vogliamo dimostrare che la scimmia verrà sempre colpita, qualsiasi sia la velocità del proiettile, se l’esploratore mirerà esattamente alla posizione della scimmia prima dello sparo, ossia nella direzione FS.

Imponiamo, allora, che, sotto le ipotesi di partenza, esista sempre un certo tempo t in cui le
coordinate del proiettile e della scimmia siano uguali. Descriviamo il moto del proiettile e della scimmia in funzione del tempo, secondo le loro coordinate x e y. Per avere l’incontro basta uguagliare x e y della scimmia e del proiettile.
Cominciamo con il moto più facile, quello della scimmia.

Al tempo zero l’ascissa dell’animale è x_S = d e l’ordinata y_S = h. Dopo di che si lascia cadere. La
cinematica più semplice ci dice che le equazioni del moto, in x e y, sono date da:

x_S = d
y_S = h – ½ gt²

L’ascissa, infatti, non cambia durante la caduta, mentre la y dipende solo e soltanto dall’altezza iniziale (costante) e dall’accelerazione di gravità g (anch’essa costante).
Passiamo al proiettile che viene sparato con una velocità qualsiasi di modulo v. Le coordinate della
velocità sono v_x e v_y. Esse dipendono dall’angolo α che caratterizza la direzione del fucile, che è stato scelta essere FS.
Al tempo zero l’ascissa e l’ordinata del proiettile sono anch’esse zero. Le equazioni del moto nelle due coordinate sono dei classici della cinematica. L’ascissa x segue un moto rettilineo uniforme, mentre la y un moto uniforme verso l’alto a cui si aggiunge (anzi si sottrae) il contributo dell’accelerazione di gravità che riduce sempre più la componente della velocità di partenza fino a un valore zero. Dopo di che il proiettile inizia a cadere sotto l’effetto della sola accelerazione g. In formule:

x_P = v_x t
y_P = v_y t – ½ gt²

Non ci resta, adesso, che uguagliare le x e le y, ossia imporre che avvenga l’incontro tra proiettile e
scimmia.

x_P = x_S
y_P = y_S

Ossia:
v_x t = d
v_y t – ½ gt² = h – ½ gt²

Ed ecco la semplificazione fondamentale che ci dice, praticamente, che sia il proiettile che la
scimmia cadono secondo la stessa legge, ossia sono in caduta libera:

v_x t = d
v_y t = h

Ricaviamo adesso il tempo t dalla prima e vediamo se è veramente uguale al t della seconda:
t = d/v_x
t = h/v_y
d/v_x = h/v_y

Ma questa relazione è sempre vera! Infatti si può scrivere:
d/h = v_x/v_y …. (1)

Per dimostrarla, basta guardare la Fig. 3, in cui i triangoli FAB e FSH sono simili. Infatti, sono entrambi rettangoli e hanno l’angolo α in comune. Notiamo che la similitudine si ha per qualsiasi valore della velocità (cambiano solo A e B, ma mantengono la proporzionalità). Ne segue, quindi che vale sempre la relazione:

FB/AB = FH/SH

Ossia proprio la (1)

La traiettoria scelta, ossia quella diretta esattamente verso la scimmia, è quella vincente.
Ricordiamo, comunque, per onestà, che basterebbe che la scimmia si spostasse di lato e tutto si risolverebbe senza alcun problema di caduta libera e di cinematica…