Questo articolo va ad arricchire il nostro archivio dedicato alla Relatività Ristretta.

 

Un classico paradosso apparente della relatività ristretta, trattato sia nella sua versione più semplice che in quella più ambigua che sembra riportarci a quello dei gemelli. La contrazione delle lunghezze è una soluzione solo mentale o decisamente fisica?

La macchina e il garage

Pippo è ormai diventato maggiorenne e il papà gli regala un’automobile di seconda mano, piuttosto lunga (i modelli più ingombranti sono quelli che costano meno), ma impone al figlio di costruire da solo un garage per contenerla. Lo invita anche a inserire un portone sia da una parte che dall’altra, in modo da poter entrare da entrambe le direzioni (la famiglia vive in campagna e ha tanto terreno attorno).

Pippo ce la mette tutta, ma la geometria e la falegnameria non sono il suo forte. Concluso il lavoro, si accorge che  la macchina è più lunga del garage. Non di tanto, ma più che sufficiente per non potere chiudere entrambi i portoni. Pippo cade in una crisi profonda e non sa come risolvere la situazione.

Alla fine chiede aiuto a Pappo, il vero genio di famiglia: chissà che non abbia costruito qualche marchingegno tale da poterlo aiutare?

Pappo ascolta con attenzione e poi dice a Pippo: “Non ti preoccupare… ti dimostro che il tuo garage è abbastanza lungo per contenere tranquillamente tutta la macchina”. Pappo invita Pippo a sistemarsi vicino al garage e ad aprire entrambi i portoni. Poi sale in macchina (anche se minorenne, sa già guidare benissimo) e traffica un poco con l’acceleratore. Dopo poco mette in moto l’automobile e si allontana di qualche centinaio di metri, per poi arrivare a velocità pazzesca, ma costante, verso il garage, proprio lungo la traiettoria che l’attraversa da portone a portone.

Pippo fatica a vedere cosa succede, ma gli sembra che, in realtà, la macchina sia sparita completamente, per un attimo, dentro il garage. Se fosse proprio così, sarebbe salvo!

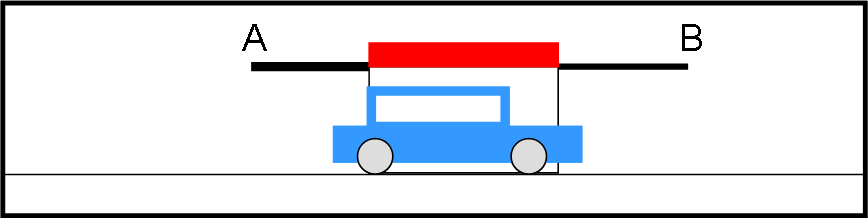
Pippo, però, vuole essere proprio sicuro di ciò che gli è sembrato di vedere e chiede a Pappo che costruisca qualcosa che gli dimostri ciò che, in cuor suo, spera ardentemente. Pappo, ci pensa un attimo e poi trova la soluzione: inserisce dei sensori nei due portoni in modo tale che nel momento in cui una delle due estremità della macchina è all’interno del garage, vicinissima a un portone, questo si chiuda e si riapra immediatamente. Pippo può benissimo rendersi conto che in un certo istante entrambi i portoni si chiudono e si riaprono all’unisono. Proprio quello che sperava di vedere. Per maggiore chiarezza chiamiamo A il primo portone e B il secondo portone.

La macchina sta perfettamente dentro il garage e le sue due estremità si trovano entrambe internamente e vicine ai portoni (ad esempio, dieci centimetri dopo e dieci centimetri prima di A e B, rispettivamente). I sensori danno il segnale di chiusura e apertura in contemporanea! Ciò che succede all’atto della chiusura-apertura dei portoni (immaginatela istantanea) lo vediamo in Fig. 1.

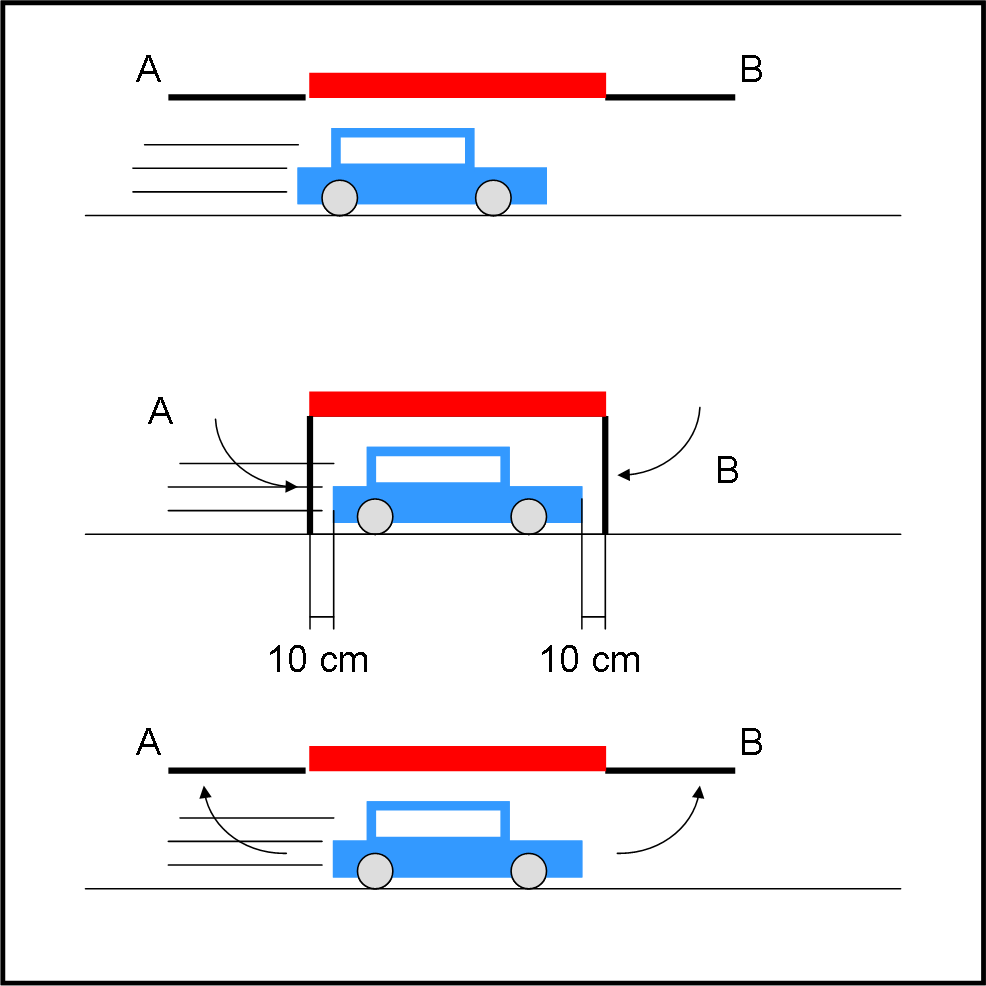
Pippo abbraccia Pappo con calore e ammirazione, senza chiedersi nemmeno come si riuscito in quella magia. Pappo, che è sempre un po’ birbante, non avendo dimenticato come il fratello cercasse di prenderlo in giro quando era piccolo, non dice altro e se ne va sghignazzando.

A Pippo non resta che mettere in pratica quanto ha fatto Pappo. Si lancia anche lui a grandissima velocità costante verso il garage. Entra all’interno di esso e vede il portone B (che dista dieci centimetri) che si chiude e subito si riapre. Tuttavia, la situazione è ben diversa da prima! Infatti, la coda della macchina è decisamente ancora fuori del portone A e quest’ultimo non può certo chiudersi. Accidenti: la lunghezza della macchina è nettamente superiore a quella del garage (Fig. 2)… Quel maledetto Pappo l’ha preso in giro.

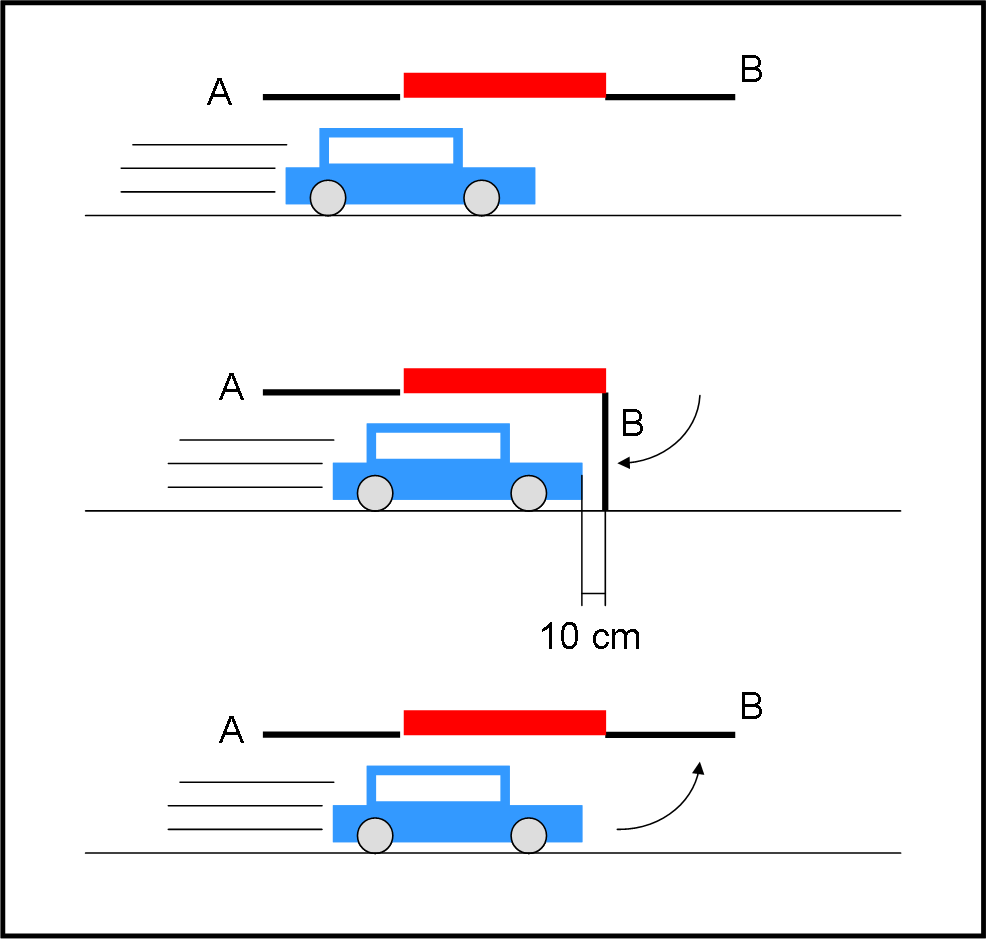
Pippo lo cerca dovunque e, finalmente, lo trova seduto tranquillo davanti al suo tavolo di lavoro (chissà che altra invenzione sta creando?!). E’ meglio non riportare le parole che Pippo scarica verso Pappo. Quando tutto si calma, Pappo prende la parola e cerca di spiegare a Pippo la teoria della relatività ristretta. Pippo lo segue attentamente, ma qualcosa non gli torna assolutamente: sarà tutto giusto, ma un certo fenomeno fisico deve rimanere identico in qualsiasi sistema di riferimento inerziale. In questo caso, invece, la macchina sta tutta dentro il garage per chi sta fermo, mentre è troppo lunga per chi sta sulla macchina.

La frase che Pippo rivolge a Pappo sembra distruggere quella strana teoria: “Caro Pappo, tu mi prendi in giro e la tua spiegazione è del tutto fasulla! In un caso riesco tranquillamente a chiudere entrambe le porte, anche se solo per un attimo, in modo che la macchina sia contenuta all’interno del garage. Nell’altro caso, riesco a chiudere solo il portone B, dato che la parte posteriore della macchina è decisamente ancora fuori dal portone A. Non posso sicuramente chiuderlo! Lo stesso fenomeno fisico dovrebbe, invece, accadere in entrambi i casi. Sarà meglio che butti giù tutto e ricominci da capo”.

Sicuramente la scelta di Pappo è quella giusta, dato che il garage deve contenere la macchina quando questa è ferma. In fondo, però, è abbastanza contento: dovrà rifare il lavoro, ma, almeno, ha smontato in pieno quella strana teoria del fratello.

Ma è proprio così?

Riassumiamo la situazione:

nel sistema di riferimento del garage, ossia quello di Pippo, se tutto è fermo (garage e macchina) l’automobile è troppo lunga per potere stare all’interno del garage e riuscire a chiudere i portoni.

Pappo dimostra a Pippo che questo problema può essere risolto facendo muovere la macchina a una velocità relativistica (comparabile con quella della luce). Essa, infatti, deve accorciarsi secondo il fattore di Lorentz, che dipende proprio dal quadrato del rapporto tra la velocità della macchina e quella della luce. Maggiore è questo rapporto e maggiore è la contrazione dell’automobile.

Pippo è più che soddisfatto e fa anch’egli la prova salendo in macchina e portandosi così nel sistema dell’automobile. Come gli spiega Pappo, la relatività ristretta deve essere simmetrica, per cui chi si trova sulla macchina è in un sistema in quiete e considera in moto (uguale e opposto) il garage.

Per Pippo è, quindi, il garage che si contrae seguendo lo stesso fattore di Lorentz (il rapporto tra le velocità è sempre lo stesso). Ne consegue che la macchina entra nel garage dalla parte anteriore (aperta) e viene a trovarsi vicinissima all’uscita in modo tale che il portone ha il tempo di chiudersi e di aprirsi nuovamente. Guardando nello specchietto retrovisore, Pippo si accorge, però, che mentre il portone posteriore ha svolto il suo ruolo perfettamente, quello anteriore non può chiudersi, dato che la macchina non è ancora penetrata all’interno del garage. Perché questo succeda, lui deve proseguire e uscire dal garage con la parte anteriore e solo in queste condizioni riuscirà a vedere anche il portone posteriore chiudersi e poi aprirsi nuovamente. Bella soddisfazione! Ha potuto toccare con mano che la sua macchina non riuscirà mi a stare tutta all’interno del garage con entrambi i portoni chiusi.

A questo punto si scatena contro Pappo e la teoria di quel fanfarone di Einstein. La simmetria vi è stata (si accorcia chi è visto muoversi), ma il fenomeno fisico finale è stato del tutto diverso da caso a caso! Nel primo, la macchina era contenuta all’interno del garage, nel secondo non lo era assolutamente.

Pappo non può che ridere… Pippo NON ha capito la relatività ristretta e, soprattutto, non ha capito che la sua base essenziale è la non simultaneità degli eventi. Dilatazione dei tempi e accorciamento delle lunghezze sono SOLO delle conseguenze di questo punto fondamentale (basterebbe leggere attentamente la parte relativa all’orologio a luce).

Consideriamo, perciò, gli eventi che c’interessano maggiormente. Essi sono: (a) entrata nel garage con la parte anteriore della macchina; (b) avvicinamento stretto (internamente al garage) del muso della macchina all’uscita posteriore (in altre parole, la chiusura e apertura del portone posteriore); (c) avvicinamento stretto (internamente al garage) della coda della macchina all’apertura anteriore (in altre parole, la chiusura e apertura del portone anteriore); (d) uscita della coda della macchina dall’apertura posteriore.

Vediamo come questi eventi si susseguono nei due sistemi.

Nel sistema del garage (Fig. 3):

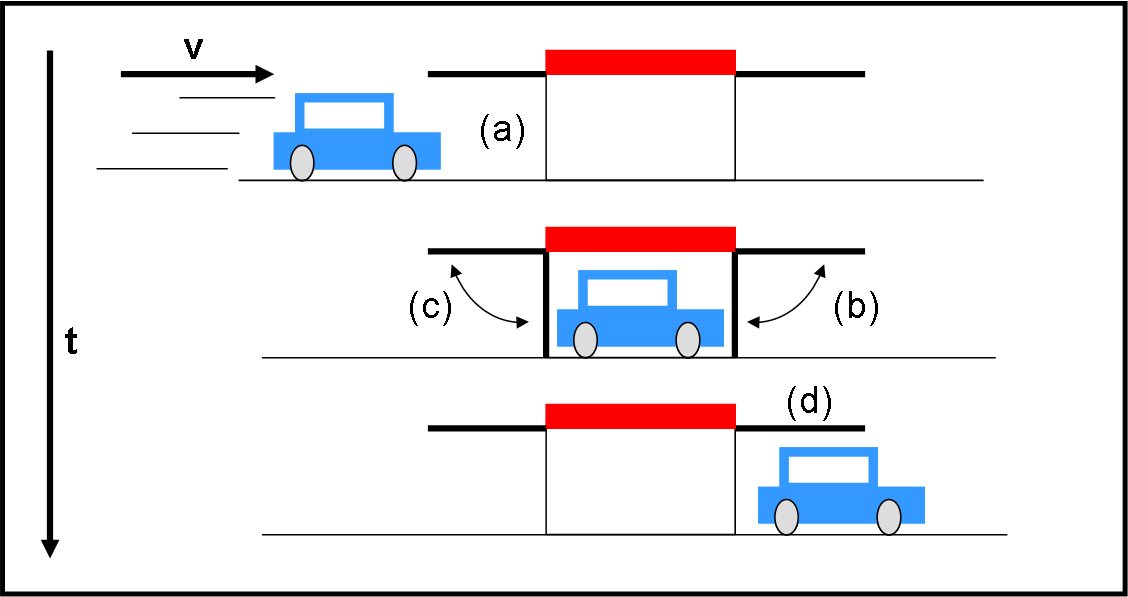
Il primo evento è (a), ossia la macchina entra nel garage dalla parte anteriore. Il secondo evento è (b), ossia la macchina è vicinissima all’uscita e il portone posteriore si apre e si chiude. Tuttavia, NELLO STESSO ISTANTE, si verifica anche l’evento (c), dato che la contrazione della macchina permette di avere la coda all’interno del garage e vicinissima al portone anteriore. Ne segue che i due eventi (b) e (c) sono simultanei. Pippo si illude che la stessa cosa avverrà anche a macchina ferma. Infine, si verifica l'evento (d).

Nel sistema della macchina (Fig. 4).

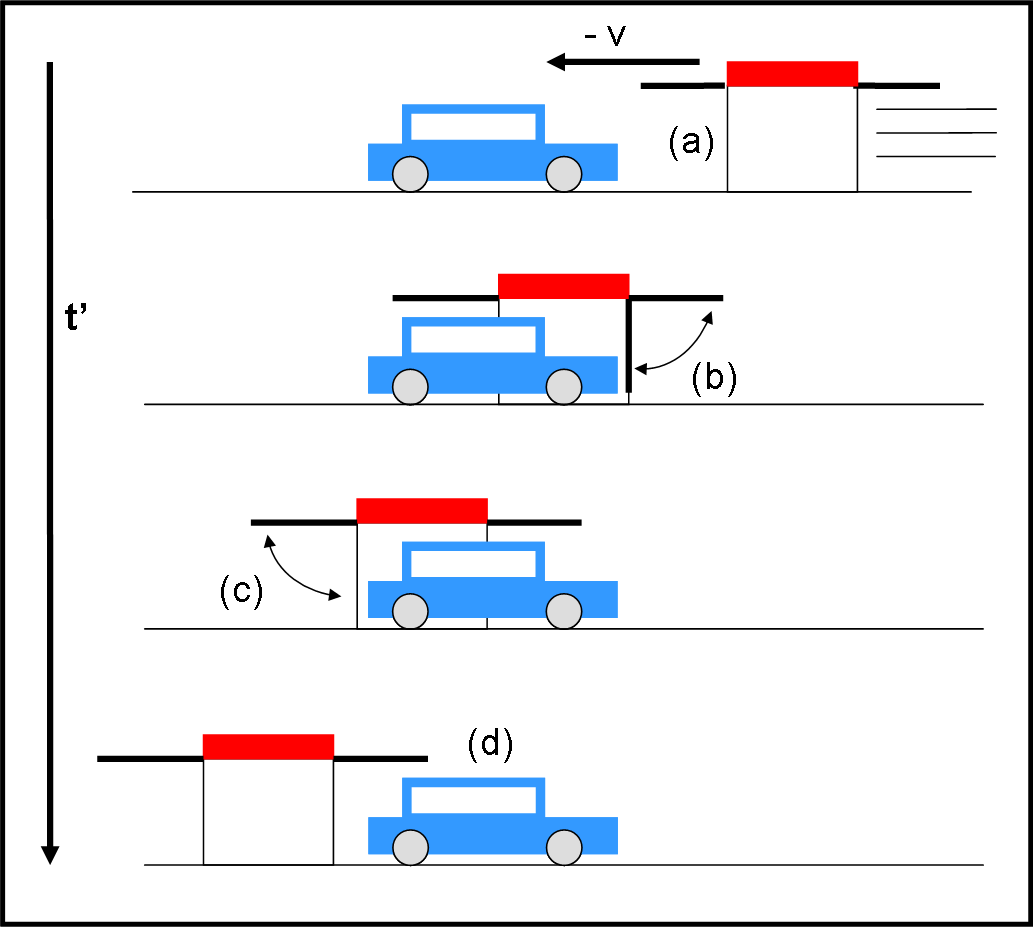
Il primo evento è nuovamente (a) e la macchina entra nel garage fino ad arrivare vicinissima all’uscita. Il portone si chiude e si apre, ossia abbiamo l’evento (b). Il portone posteriore non può fare niente dato che l’automobile sta ancora transitando. Il muso della macchina sarà giù uscito dalla parte posteriore quando finalmente la coda entra all’interno del garage e fa chiudere e riaprire il portone anteriore. A questo punto si verifica l’evento (c), decisamente DOPO che si è verificato l’evento (b). Infine, la macchina esce completamente verificando l’evento (d).

Gli eventi sono stati del tutto simili (ossia il fenomeno fisico è stato lo stesso). L’unica differenza è stata la differenza di tempo tra gli eventi (b) e (c). Nel sistema del garage sono avvenuti nello stesso istante, in quello della macchina in tempi diversi. Ma tutto ciò è PERFETTAMENTE consistente con la relatività ristretta che si basa proprio sulla relatività della simultaneità.

Il paradosso è completamente risolto e Pippo deve ricominciare a costruire il suo garage…

Seguendo quanto descritto a parole non è assolutamente difficile rappresentare il tutto in modo ancora più chiaro e immediato, utilizzando il diagramma di Minkowski.

Minkowski semplifica e sintetizza

Portiamoci nel sistema di riferimento del garage, immaginato in quiete. Il garage descrive, perciò, una striscia perpendicolare all’asse delle x, che è la sua striscia di universo in questo sistema di riferimento (Fig. 5). L’importanza di questa striscia è grande, in quanto ci permette di lasciarlo invariato in ogni altro sistema. Ciò che cambia è la linea di simultaneità che varia a seconda della velocità impressa alla macchina. Ogni sistema “vede” una certa sezione della striscia composta da eventi diversi. In altre parole, la nostra striscia-muro è l’insieme di tutti gli eventi relativi ai vari sistemi. Tra poco ne vedremo l’utilizzo immediato.

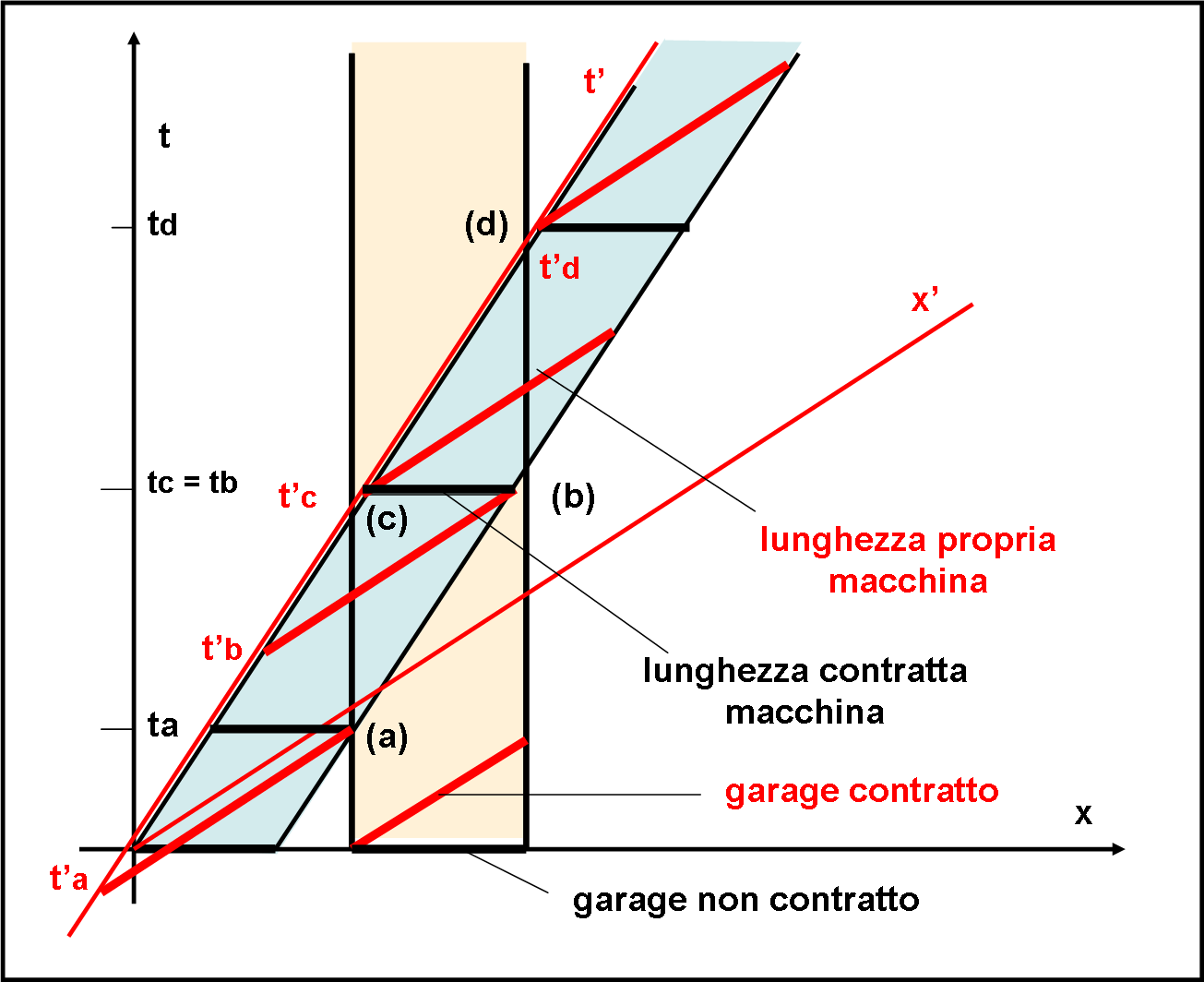
Nel sistema del garage è immediato ottenere la lunghezza ridotta della macchina (attraverso l’iperbole di calibrazione) e tracciare la linea che corrisponde a una certa velocità. In questo sistema il garage mostra la sua lunghezza propria che è data dalla sezione della sua striscia di universo (rosa) lungo l’asse delle x. La macchina in movimento sarà determinata dalla sua lunghezza ridotta lungo l’asse x e descrive la  striscia inclinata (azzurra). Per come sono stati scelti i parametri la sequela degli eventi è data da: a, entrata macchina nel garage;  b e c simultanei, chiusura e apertura di entrambi i portoni; d, uscita macchina dal garage.

Notiamo come la simultaneità di b e c sia un caso peculiare. Se la macchina si fosse “contratta” ancora di più, avrebbe avuto più tempo per restare all’interno del garage e l’evento (c), chiusura e apertura portone anteriore, anticiperebbe l’evento (b), chiusura e apertura portone posteriore. Tuttavia, Pappo ha scelto il caso limite per fare più “scena” col fratello…

Le linee nere di Fig. 5 riportano quanto detto finora (sistema di riferimento del garage).

Portiamoci, adesso, nel sistema in moto con la macchina (linee rosse). L’asse t’ è già stato tracciato e coincide con la linea che definisce la velocità della macchina. L’asse x’ è costruito facilmente ribaltando l’asse t’ rispetto al cono di luce (velocità della luce). La macchina che è adesso in quiete nel sistema (x’, t’) mantiene la sua lunghezza propria, sicuramente maggiore di quella del garage da fermo e, a maggior ragione, di quella del garage contratto.

Qual è la sezione del garage contratto? Presto detto la sezione della sua striscia di universo lungo l’asse x’. Non fatevi ingannare dalle apparenze! Essa sembra più lunga di quella del garage in quiete, ma non è vero, dato che siamo su un sistema diverso. Basterebbe costruire nuovamente l’iperbole di calibrazione per vedere come questa sezione sia veramente contratta.

Non ci resta allora che far muovere la nostra macchina verso destra (Attenzione! In realtà dovremmo far muovere la striscia del garage verso sinistra, ma il risultato sarebbe del tutto identico). Si riconoscono nuovamente gli eventi che ci interessano: a,b,c,d. Tuttavia, essi si riferiscono a tempi t’ diversi e separati. Prima abbiamo (a) con la parte anteriore della macchina che entra nel garage, poi (b) in cui la parte anteriore fa chiudere ed aprire il portone posteriore, poi (c) in cui, finalmente, la parte posteriore della macchina entra nel garage, mentre quella anteriore è giù uscita. Infine abbiamo (d) in cui tutta la macchina esce dal garage.

La macchina non sarà mai racchiusa completamente nel garage, ma la simmetria della RR è perfettamente conservata dato che gli eventi si ripetono, a parte una diversa simultaneità (del tutto ammessa dalla RR). Notiamo che la striscia azzurra della macchina è anch’essa una striscia di universo, riportata però a un sistema che non  è (x,t), ma (x’,t’). Rispetto a tale sistema la traccia parallela a x risulta, ovviamente, ristretta.

E se bloccassimo l'uscita del garage?

Nell'esercizio mentale che abbiamo appena  trattato, sia qualitativamente che attraverso Minkoski, la soluzione del paradosso non pretendeva che la macchina entrasse e fosse chiusa nel garage in entrambi i sistemi di riferimento, ma solo e soltanto che le due porte si chiudessero ed aprissero, entrambe all’avvicinarsi (interno) della macchina. La soluzione era ovvia se solo ci si ricordava che nella relatività ristretta non si mantiene la contemporaneità di due eventi, cambiando sistema di riferimento, come d’altra parte mostra molto bene la fascia di universo a mano a mano che viene tagliata dall’asse di simultaneità di un sistema in movimento a velocità variabile.

L’ulteriore complicazione è la seguente: immaginiamo di bloccare ermeticamente il portone posteriore del garage. Nessun problema per il sistema del garage. La macchina entra completamente dentro, attraversando e permettendo di chiudere il portone anteriore, senza avere contatti con la parte posteriore. Il fenomeno fisico è soltanto l’entrata della macchina completa dal portone anteriore. Purtroppo questo fenomeno fisico non sembra capitare nel sistema della macchina. Lei arriva fino al portone posteriore chiuso, ma è costretta a fermarsi senza essere passata completamente dal portone anteriore, che quindi non può chiudersi. Il fenomeno fisico è diverso e ciò non può succedere.

Il problema, in poche parole, è il seguente: chiudiamo ermeticamente il portone posteriore. Quando la macchina è tutta dentro al garage possiamo anche chiudere ermeticamente il portone anteriore.

Nessun problema nel sistema di riferimento del garage, come abbiamo visto nella Fig. 5 .La macchina si troverà sicuramente in quelle condizioni.

Più "maligno" è il caso in cui il sistema di riferimento della macchina. Utilizziamo nuovamente la Fig. 5, ma bloccando il portone posteriore. Al tempo t'_b la parte anteriore della macchina urta contro il portone posteriore chiuso e non proseguire.

Tuttavia, la parte posteriore della macchina non sa ancora che la sua parte anteriore è stata bloccata e deve quindi aspettare il segnale di stop che si trasmette dal punto dell'urto verso il resto della macchina che sta ancora viaggiando. Per veloce che vada l'informazione non può superare la velocità della luce e, quindi, non è difficile disegnare la traiettoria di questa informazione (linea verde) in Fig. 6, fino all'incontro con l'ultimo punto della macchina. In quell'istante, t'_f , tutta la macchina può fermarsi e risulta abbondantemente all'interno del garage e la macchina, essendo ferma, risulta essere nel sistema del garage (lo è diventata punto a punto a mano a mano che l'informazione arriva a dare lo stop). Si può chiudere tranquillamente anche il portone anteriore. Si nota molto bene come la macchina si sia notevolmente contratta (AB), ma in modo che più fisico di così non si può...

Cosa succede alla parte tratteggiata all'interno del triangolo verde? Tutto dipende da che composizione fisica diamo alla macchina... se è elastica si schiaccia per poi tornare alle dimensioni iniziali (e sfondare il portone anteriore, come fa anche nel caso in cui tutto è visto dal sistema del garage), altrimenti potrebbe sgretolarsi in mille pezzi. Ma questo, nell'esperimento mentale, poco importa...

Figura 6

Paradosso risolto, ma... siamo nelle condizioni del paradosso dei gemelli (quello era di tipo temporale, questo di tipo spaziale). Entrambi i sistemi di riferimento sono costretti ad ammettere che la macchina risulta sempre più corta del garage, così come nel paradosso dei gemelli, il gemello viaggiatore risultava effettivamente il più giovane. La faccenda si risolve concettualmente in fretta, ricordando che sia per i gemelli che per il portone inamovibile è necessario introdurre una accelerazione e/o decelerazione, trattabile, comunque, con la sola RR.

Non chiedetemi cosa succeda dopo che le macchine sono state bloccate... sfondamento del portone anteriore? esplosione? accartocciamento? Tutto dipende dal modello fisico che adottiamo per la nostra macchina.

Piccola provocazione: ammettiamo che la contrazione relativistica sia solo "apparente"... Come spiegarsi, allora, i danni subiti dalla macchina quando riprende le sue dimensioni in quiete?