Categorie: Relatività
Tags: fattore di Lorentz la favola di Muo lunghezze proprie e improprie relatività ristretta tempo improprio velocità della luce
Scritto da: Vincenzo Zappalà
Commenti:16
Un quiz arrivato dall'esterno... *
Un lettore (silenzioso ufficialmente) mi ha prospettato un quesito di cui ho piacere di rendervi partecipi (poteva anche inserirlo direttamente come commento...).
Riporto tale e quale la sua domanda:
"Io, che sono "fermo", osservo un nave stellare che, facendo partire un raggio di luce da poppa, raggiunge la pura percorrendo 21,598 dei "miei" metri, Riflesso, tale raggio ritorna alla poppa percorrendo 6,506 metri.
Posso determinare il Fattore di Lorentz, la velocità della nave e la sua lunghezza?"
Invito, anche i meno esperti, a tentare la risposta (non il lettore a cui ho già risposto, però!). La visione nello spaziotempo di Minkowski è anche gradita. Ovviamente con La Favola di Muo tra le mani tutto diventa banalissimo...
Preferirei che usaste i simboli e non i numeri, per rendere il tutto più generale.






16 commenti
Ho fatto il seguente ragionamento, con la RR non ho ancora molta padronanza, per cui chiedo venia per eventuali strafalcioni , più che altro consideratelo un mio mettermi alla prova
In effetti La favola di Muo aiuta parecchio, in particolare il paragrafo in cui si mette in orizzontale l'orologio a luce..
Chiamo L1 la lunghezza percorsa dalla luce che parte dalla poppa e arriva alla prua dell'astronave in movimento con velocità V , lunghezza misurata dall'osservatore fermo. Chiamo, invece, con L' la lunghezza dell'astronave come misurata dall'osservatore fermo (quindi contratta).
Naturalmente, anche se la luce in questa prima fase si muove nello stesso verso dell'astronave , per l'osservatore fermo la sua velocità è pur sempre c. Per cui, se chiamo t1 il tempo misurato dall'osservatore fermo perché la luce partita dalla poppa arrivi alla prua, esso sarà dato da:
t1 = L1 / c (1)
Per l'osservatore fermo, in tale tempo t1 la luce coprirà una distanza data da:
c*t1 = L' + v*t1 (2)
cioè pari alla somma della lunghezza dell'astronave, come da lui misurata (quindi contratta) , e dello spazio percorso dall'astronave (che si muove a velocità V) nel tempo t1.
Il tempo t1 lo sappiamo, perché attraverso la (1), sapendo L1 (che è un dato del problema = 21,598 m) , possiamo immediatamente calcolarcelo. Dalla (2), allora, sostituendo a t1 l'espressione della (1) , mi ricavo L':
L' = (c-v)*L1/c (3)
Passo ora alla seconda fase, cioè al ritorno della luce dalla prua alla poppa. Anche in questo caso, L' è sempre quella (contratta) , la velocità della luce per l'osservatore fermo è ancora
c , anche se stavolta la luce va in verso opposto all'astronave) e quindi, il tempo t2 che la luce impiega , per l'osservatore fermo, per andare dalla prua alla poppa sarà dato da:
t2 = L2 / c
e vale la relazione:
c*t2 = L' - v*t2
cioè, stavolta, la distanza coperta dalla luce per l'osservatore fermo è data dalla differenza tra la lunghezza dell'astronave, come da lui misurata (quindi contratta), e lo spazio percorso dall'astronave nel tempo t2. Anche in questo caso, mi ricavo L':
L' = (c+v)*L2/c (4)
A questo punto, confronto la (3) e la (4) ottenendo dopo qualche passaggio:
v= c*(L1-L2)/(L1+L2)
Una volta nota V, posso calcolari il fattore di Lorentz e la lunghezza propria dell'astronave .
Avrò compreso bene oppure ho fatto solo una gran confusione ? Prof, chiedo clemenza
Provo a farlo nello spazio di Minkowski, sfruttando le simmetrie geometriche.P-P1-P2 è il percorso del raggio di luce .
l è la lunghezza della astronave, v la sua velocità. L1, L2 le distanze orizzontali percorse nel primo e secondo tratto.
Consideriamo c=1: In tal modo l'angolo formato con dalla luce con rette parallele o perpendicolari agli assi è 45°; dal disegno risulta che:
l+L1 v=L1
l-L2v=L2
per cui l=L1-L1*v
l=L2+L2*v
da cui L1-L1*v=L2+L2*v,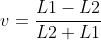
Fattore di Lorentz:
l=L1-L1*v=L1-L1*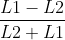
grazie Umberto! Notate come il diagramma di Minkowski permetta infinite variazioni sul tema. Saperlo leggere vuol dire entrare veramente nell'Universo!
Anche se l'angolo teta non serve più di tanto...
Caro Enzo, vorrei provare anch’io a rispondere a questo quiz.
Dunque per il sistema considerato in quiete, il raggio di luce percorre una distanza d1 per raggiungere la prua dell’astronave pari a 21,598 metri (in Italia la virgola la considero un separatore dei decimali).
Tale distanza per il sistema in quiete è pari a:
d1 = v Δt1 + L
Dove L è la Lunghezza dell’astronave per il sistema in quiete.
Lo stesso raggio di luce per tornare indietro, percorre una distanza d2 pari a 6,506 metri.
Tale distanza per il sistema in quiete è pari a:
d2 = L - v Δt2
Per cui:
L = d2 + V Δt2
Sostituendo L nella prima formula ottengo:
d1 = v Δt1 + d2 + v Δt2
d1 - d2 = v Δt1 + v Δt2
d1 - d2 = v (Δt1 + Δt2)
La velocità della luce è uguale per ogni sistema di riferimento ed il raggio di luce per compiere un andata e un ritorno (come un orologio luce posto sull’astronave in orizzontale) impiega, per il sistema in quiete, un intervallo di tempo Δt = (Δt1 + Δt2)
In tale intervallo di tempo la luce percorre per il sistema in quiete la distanza d = d1 + d2, per cui:
Δt = (d1 + d2)/ c
Ora non resta che sostituire quanto trovato nella formula precedente:
d1 - d2 = v (Δt1 + Δt2)
d1 - d2 = v Δt
(d1 - d2) = v (d1 + d2)/c
v/c = (d1 - d2)/(d1 + d2) = 0,537 c
In questo modo si trova la velocità dell’astronave in rapporto a quella della luce (v/c), misurata dal sistema in quiete.
Una volta stabilita la velocità dell'astronave è un attimo trovare il fattore di Lorentz, ossia:
γ = 1/√(1- v²/c²) = 1/√1- (d1 - d2)²/(d1 + d2)² = 1,185
Considerato che:
Δt2 = d2/c (tempo impiegato dalla luce per percorrere la distanza d2, secondo il sistema in quiete)
La Lunghezza dell’astronave per il sistema in quiete è pari a:
L = d2 + v Δt2 = d2 + v d2/c
L = d2 (1 + v/c) = 9,999 metri
Ovviamente per il sistema in quiete la lunghezza L è contratta rispetto a quella propria dell’astronave (L0), ossia:
L0 = L γ = L/√(1- v²/c²)
L0 = L//√1- (d1 - d2)²/(d1 + d2)² = 11,853 metri
Spero di non aver sbagliato qualcosa.
Paolo
carissimo Paolo... che ne dici di dare anche la rappresentazione nel diagramma di Minkowski...?
caro Umberto...
volendo considerare che v = tan(90 - teta)
bastava fare
v = (L1 - L2)/(t1 + t2)
dato che t1 e t2 sono noti... non ti pare?
mi e venuto cosi..
Caro Enzo, anche se in fretta, posso aggiungere questa immagine, che usa il diagramma di Minkowski.
Giusto per mostrare la situazione....
Paolo
Bene, penso che come al solito non si muoveranno i poco esperti per tentare di dire la loro... L'importante è che seguano i commenti e poi la soluzione.Grazie amici!
Buongiorno, tento una soluzione geometrica con Minkowski, l’ho fatto un po’ di fretta, tiratemi le orecchie al minimo errore.
L1 è la lunghezza percorsa dalla luce verso la prua ed è nota=21,598 m (nel sist di riferim. in quiete).
L2 è la lunghezza percorsa dalla luce nel suo viaggio di ritorno verso poppa ed è parimenti nota=6,506 m (sempre nel sist. in quiete).
Il rapporto tra queste 2 quantità è legato alla velocità v dell’astronave, se fosse ferma varrebbe 1, al crescere della velocità v il rapporto tra le due quantità cambia perché la luce, viaggiando sempre a velocità c fissa, si trova a percorrere più spazio all’andata e meno al ritorno.
I tempi di percorrenza conservano il medesimo rapporto, nel ns caso: 21,598/6,506=3,32 (approssimato).
Passo a sfruttare Minkowski. Nel sistema di riferimento in quiete individuo sull’asse t due punti rappresentativi di 2 istanti t1 e t2 relativi ai momenti in cui la luce arriva a prua (t1) e arriva a poppa (t2), i due punti devono avere ordinate tali che i segmenti individuati siano conseguenti ed abbiano lunghezze in rapporto 3,32.
Ora, partendo dall’origine O, che pongo sia l’istante in cui parte il raggio di luce, traccio la traiettoria della luce (linea gialla) di andata inclinata di 45°. All’istante t1 la luce arriva a prua, quindi l’intercetta della linea parallela (in tratteggio) all’asse s con la linea della luce individua l’istante di arrivo della luce a prua (punto rosso).
Dal punto rosso la luce riparte per riflessione sullo specchio e torna verso poppa, quindi traccio la perpendicolare, sempre in giallo, essa intercetterà la linea tratteggiata dell’istante t2 nel punto viola. Posso ora tracciare la retta rossa passante per O e per il punto viola, che rappresenta l’asse t’ del sistema di riferimento solidale con l’astronave.
E’ ora possibile tracciare la retta x’ simmetrica della retta t’ rispetto alla retta gialla della luce, ottenendo l’altro asse (x’) del sistema di riferimento dell’astronave. L’angolo in O (azzurro), che chiamo θ, è direttamente collegato con il valore di v dalla relazione tgθ=c/v ed è pure identificabile tramite il coeff. angolare della retta x’ nel piano cartesiano con gli assi in nero.
Seguendo la costruzione grafica mi sembra, se non sbaglio qualcosa, che il valore di v si possa calcolare facendo uso delle sole relazioni di geometria analitica.
ottimo Guido. Potresti anche dirmi facilmente come calcolare quell'angolo dai dati che hai... (Un banale triangolo rettangolo...).
Senza aggiungere figure, che impiego sempre molto tempo a fare: gli angoli xOx' e tOt' sono uguali, nel triangolo individuato dai vertici t2, O e dal punto viola faccio il rapporto tra la misura del cateto minore e quello maggiore, il rapporto corrisponde alla tangente dell'angolo (che è poi il coeff. angolare della retta x'). Ne calcolo l'arcotang. e ottengo l'angolo.
ma conosci il cateto minore? e poi che te ne fai dell'angolo? ricorda che vogliamo conoscere v e lunghezza della nave... rifletti e vedrei che è molto semplice...
è mio dovere aggiungere che la formula per v data da Umberto è esattamente quella che si trova in modo -forse- più rapido, ricordando che t1 + t2 = L1 +L2, dato che L1 = t1 e L2 = t2 per c = 1
Buongiorno, completo l’esercizio, anche se in ritardo. Indico con 1 l’estremo della lunghezza L1 (percorso della luce misurato dall’osservatore in quiete), il segmento con estremi 2 e 1 corrisponde quindi al percorso di ritorno della luce (sempre misurato nel sistema in quiete). Nel triangolo rettangolo 2OP posso fare il rapporto tra i cateti 2P/2O. Ma 2P/2O=tg(90-θ) e quindi 2P/2O=1/tgθ da cui tgθ=2O/2P. Ma il segmento 2P corrisponde a L1+L2 mentre 2O corrisponde a L1-L2, quindi tgθ=(L1-L2)/(L1+L2) ed è la velocità della nave, espressa in frazione di c. A me risulta essere appena più della metà di c, tgθ=0,537.
Per trovare la lunghezza propria dell’astronave, ragionando analiticamente sul diagramma, considero l’intersezione tra la retta parallela all’asse t’ (y=(1/tgθ)x) e passante per Q (L1, t1) e l’asse x’, di eq. y=tgθx, il segmento così individuato sull’asse x’ è la lunghezza propria dell’astronave.