Un esercizio perfetto per chi ama la geometria e detesta l'algebra. Ciò che si deve fare è solo tagliare, ruotare, traslare e incollare ... peccato che nessuno abbia avuto voglia di provarci. Riassumiamolo come dimostrazione di un teorema.

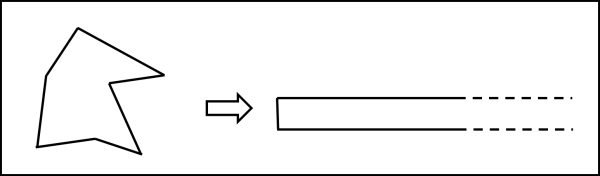
I due poligoni della figura sono equivalenti, ossia hanno la stessa area? L'unica cosa che dobbiamo fare è trovare un metodo che ci permetta di dimostrarlo. Il vero obiettivo non è tanto la conclusione, ma il metodo usato per trovarla (ne esiste più di uno...)

Tuttavia, vi sono alcune regole da rispettare:

possiamo solo TAGLIARE, TRASLARE e  RUOTARE  (eventualmente INCOLLARE). Nessun  calcolo e nessuna misura sono permessi attraverso righelli, squadre, compassi o qualsiasi altro marchingegno tecnologico. Il righello, senza tacche, può essere usato solo per tracciare linee rette. Al limite possiamo PIEGARE, se non abbiamo molto occhio.

La strategia scelta è abbastanza semplice: trasformare il poligono in un rettangolo di lato unitario. Qualsiasi poligono può subire la stessa sorte. Se, però, l'area deve essere uguale, è ovvio che tutti i poligoni di uguale area devono trasformarsi nello stesso rettangolo e, di conseguenza, è facile scomporre il rettangolo in qualsiasi poligono di uguale area, applicando il procedimento inverso. Dedichiamoci, quindi, alla scomposizione del nostro esagono, preso come esempio, ma è chiaro che si poteva partire da qualsiasi poligono equivalente.

(1) Tagliamo il poligono in triangoli che non abbiano punti in comune

Operazione veramente banale e poco importa se vi sono diverse possibilità per farlo: basta sceglierne una qualsiasi. La Fig. 1 mostra il nostro taglio... A questo punto abbiamo 5 triangoli del tutto diversi. Ruotiamoli per chiarezza in modo da mettere uno dei loro lati su una linea orizzontale.

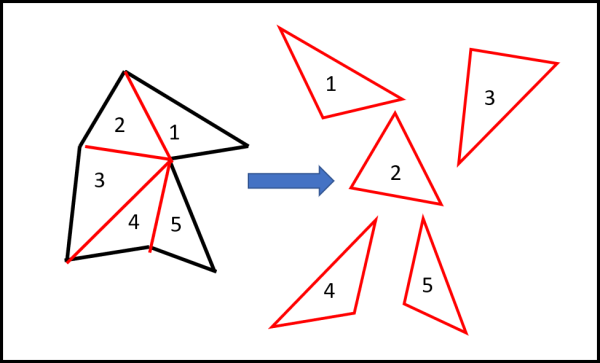
(2) Trasformiamo i triangoli in rettangoli

La Fig. 2 ci mostra cosa fare per ciascuno di essi.

 

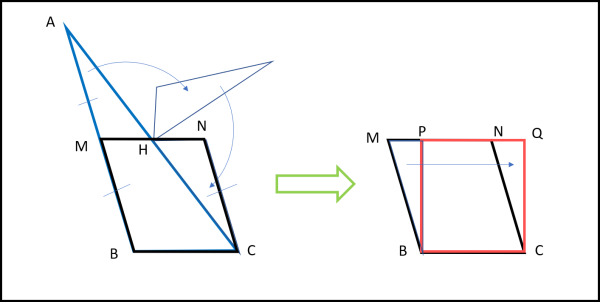
Il triangolo sia ABC. Tagliamo il triangolo lungo MH. M è il punto che sta a metà di AB e per trovarlo basta piegare il triangolo in modo che A e B coincidano. Idem per H. Il triangolo AMH lo ruotiamo come mostra la figura fino a farlo coincidere con HNC. In tal modo il triangolo si è trasformato nel parallelogramma AMC.  Tagliamo, adesso, lungo la linea PB che è facilissima da tracciare piegando la parte sinistra del parallelogramma in modo che AB cada sul segmento PN. Trasliamo il triangolo MPB, portandolo nella posizione NQC. Perfetto! Il triangolo iniziale ABC è stato trasformato nel rettangolo PQCB che ha la sua stessa area.

Facciamo la stessa cosa per tutti i cinque triangoli dell'ettagono di partenza e otteniamo cinque rettangoli con i lati probabilmente (se non avete avuto una fortuna particolare) diversi tra loro, come mostra la Fig. 3.

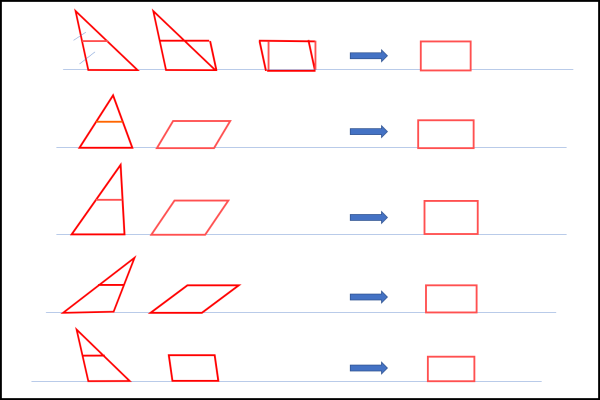
(3) Trasformiamo i rettangoli in rettangoli che abbiano tutti un lato uguale all'unità

Questa operazione è forse leggermente più difficile, ma spieghiamola passo dopo passo... utilizzando la Fig. 4

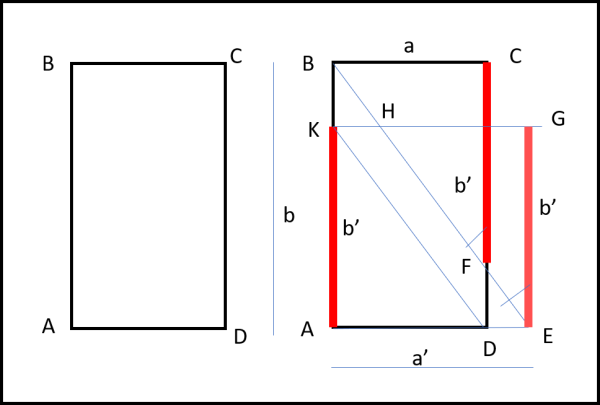
Il nostro rettangolo sia ABCD e poniamolo, per semplicità, con il lato più corto in orizzontale. Riportiamo la nostra unità b' (l'unica che ci serve per misurare qualcosa) lungo il lato AB = b (b' < b), partendo da A e troviamo il punto K. Facciamo lo stesso sul lato CD, partendo da C e otteniamo il punto F. Abbiamo, ovviamente,  AK = CF e quindi anche BF = FD. Tagliamo il triangolo BCF e facciamolo scivolare fino a che non arrivi a toccare la linea orizzontale. Esso diventa HGE. Ovviamente GE = b'. Tagliamo il triangolo BKH e trasportiamolo nella posizione DFE. I due triangoli BKH e DFE sono sicuramente uguali dato che hanno i tre angoli uguali e i lati BK e FD anch'essi uguali per costruzione. In tal modo abbiamo costruito il nuovo rettangolo AKGE che ha come lato verticale proprio l'unità b'. Non ci resta che dimostrare che l'area di ABCD sia la stessa di AKGE. I triangoli ABE e AKD sono chiaramente simili, avendo gli angoli uguali. Possiamo allora scrivere:

AE : AD = BA : KA

O ancora:

AE · KA = AD · BA

a'· b' = a · b

Le due aree sono uguali, ossia i rettangoli sono equivalenti.

(4) Otteniamo un solo rettangolo

Possiamo adottare la stessa procedura per tutti i rettangoli di Fig. 3 e ottenerne 5 aventi tutti lo stesso lato b', uguale all'unità. Non ci resta che unirli tra loro e costruire un solo rettangolo che ha per lato minore b' e per lato maggiore la somma degli altri lati

b'a'1 + b'a'2 + b'a'3 + b'a'4 + b'a'5 = b'(a'1 + a'2 + a'3 + a'4 + a'5)

In conclusione, il rettangolo finale ha la stessa area della somma dei cinque rettangoli i quali hanno la stessa area dei rettangoli precedenti che hanno la stessa area dei triangoli che hanno la stessa area dell'ettagono di partenza. Siamo riusciti a trasformare il poligono irregolare di partenza in un rettangolo di lato unitario. Lo stesso procedimento vale per qualsiasi poligono. Possiamo perciò dire che qualsiasi poligono è equivalente a un rettangolo di lato unitario. Se i rettangoli finali risultano uguali, i due poligoni di partenza devono avere la stessa area (provare per credere...).

Quanto abbiamo dimostrato era già stato intuito da Euclide (sempre lui!), nei suoi "Elementi", ma viene oggi enunciato in modo accurato dal  Teorema di Wallace-Bolyai-Gerwien. Esso dice in modo stringato: "Due poligoni equivalenti sono equiscomponibili". Per come abbiamo dimostrato il teorema possiamo anche dire che ad ogni poligono di uguale area può essere associata la lunghezza di un segmento, dato che ogni poligono può essere ricondotto a un rettangolo di lato unitario (la sua area è quindi uguale al valore del segmento).

Il grande Hilbert,  si pose il problema più generale (detto anche "terzo problema di Hilbert") chiedendosi se fosse possibile estendere il teorema anche ai solidi di pari volume. Max Dehn dimostrò nel 1902, mediante lo sviluppo della teoria degli invarianti, che questo non è possibile, se non in casi particolari.

Per adesso, limitiamoci alla geometria piana e divertiamoci a scomporre e ricomporre poligoni di forme diverse (ma che abbiano la stessa area!).

P.S.: questo articolo ci riporta a questo vecchio "gioco" (un semplice ed economico regalo di Natale per bambini che vogliono usare la testa...?)