LA SFERA DI POINCARÉ : 7) La curvatura in una curva piana ***
Gli altri articoli di questa serie (LA SFERA DI POINCARÉ) , li trovate nel'archivio--> Matematica e geometria-->Matematiche pure
Riprendiamo i nostri discorsi sulle varietà Riemmane; ci resta da definire una delle cose più importanti su di esse; la curvatura. La curvatura può riguardare le varietà di qualsiasi dimensione; noi cominceremo dalle varietà di dimensione 1 , ovvero dalle curve immerse nel piano. Continuiamo a parlare di varietà immerse, perchè così siamo abituati per lavorarci; vedremo però che ci sono varietà che non richiedono alcuna immersione per esistere, ma solo la definizione di metrica definita in esse. Il discorso sarà breve e semplice; abbiamo già parlato di curve parametriche e del concetto di velocità in una curva in questo articolo.
Per semplicità parleremo come già detto di curve piane (ovvvero che stanno in un piano, non nello spazio). Riprendo quanto detto nell'articolo a riguardo.
L'equazione di una curva e il vettore velocità
Tutti abbiamo in mente cosa sia una curva nel piano cartesiano. Di solito, però, si è soliti dare le curve per equazione, come ad esempio l'equazione della circonferenza, ovvero le coppie (x,y) di punti del piano che soddisfano per esempio l'equazione:
altra cosa è dare una curva per parametri. In genere, per una curva piana, si dà una applicazione e si specifica la corrispondenza fra un parametro (di solito indicato con t) e un punto del piano, cioè
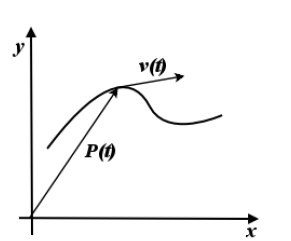
Questo tipo di equazioni ha senz'altro origine da problemi riguardante il moto di un punto; se consideriamo ad esempio un moto parabolico, x,y sono le due coordinate lunghezza e altezza, mentre t è il tempo:
1)
risulta quindi naturale definire il vettore velocità, v, derivando le due componenti rispetto al parametro t:
oppure,con una notazione un p0' più vettoriale:
2)
(i,j) sono i versori dell'asse x e y)
risulta allora evidente l'analogia con la velocità del moto in 1); essa è rappresentata proprio dalle formule appena viste:
La lunghezza di una curva
Nell'articolo 6 della serie su Poincarè abbiamo fatto un ulteriore passo avanti, definendo la lunghezza di una curva , in funzione della metrica definita in quella data varietà (in realtà in quel caso abbiamo calcolato la distanza fra due punti prendendo la curva di minima lunghezza che li unisce). Abbiamo visto come la lunghezza della curva sia legata al vettore tangente che ci dà lo spostamento infinitesimo su di essa. Ma il vettore tangente altro non è che il vettore velocità. Nel caso piano le formule si semplificano di molto; la curva parametrica che chiameremo ha un solo parametro, che chiameremo t, e sarà definita in un certo intervallo I. Formalizzando ulteriormente:
Per calcolare la lunghezza di una curva basta sommare i pezzettini infinitesimi , che si ottengono facilmente dal vettore velocità:
quindi per trovare la lunghezza della curva, basta integrare:
essendo la velocità vettoriale, data in modulo, uguale a l'integrale si può scrivere in modo più compatto cosi:
e questa è l'unica formula che è bene ricordare. Qualcuno mi dirà: ma cosa centra questo con la curvatura? Lo vedremo fra poco.
Due parole (intuitive) sulla parametrizzazione di una curva
E importante osservare che una curva non è semplicemente un sottoinsieme di punti di (cioè la traiettoria descritta dal punto P(t)) ma è una funzione di I in
. Due equazioni parametriche diverse, per esempio:
x = t
y = con t>0
e
x =
y =
con t'
individuano due curve parametrizzate distinte, pur descrivendo la stessa traiettoria (come si vede facilmente sostituendo t con ). Intuitivamente, possiamo pensare alla stessa curva percorsa in tempi diversi.Ovvero con velocità diverse. Un conto è la traiettoria, che si chiama supporto della curva, e un conto è la curva vera e propria. Si vede subito calcolando il vettore velocità. Indipendente è invece la lunghezza della curva. Pensate, fra le parametrizzazioni che definiscono la stessa traiettoria, c'è nè una che ha addirittura velocità costante e uguale a 1; quella che definiamo fra poco.
La funzione arco
Se nell'integrale , fatto nell'intervallo [t0,t1], lasciamo libero l'estremo superiore , otteniamo una funzione di t , definita sempre in [t0,t1],
, dove è stata cambiata la variabile di integrazione per non fare confusione. Sappiamo che v è positiva, infatti
; la funzione s(t) è pertanto una funzione crescente in [t0,t1], e quindi biunivoca e invertibile. Quindi, se l è la lunghezza della curva,
La funzione P(s) (ossia la curva avente come parametro l’arco) si dice parametrizzazione naturale della curva, e gode della seguente importante proprietà:
La velocità rispetto alla parametrizzazione naturale è unitaria.
Siamo adesso pronti per definire il concetto di curvatura:
Definizione di curvatura.
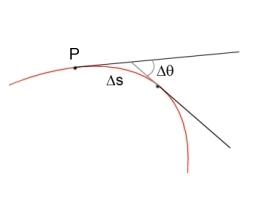
Vogliamo definire formalmente la curvatura di una traiettoria nel piano in un punto. Intuitivamente, più velocemente varia la direzione di un punto che la percorre, maggiore è la curvatura. Possiamo allora considerare la figura1; Vogliamo definire la curvatura in P (ripeto;la curvatura si può definire solo in un un punto) . Traccio la tangente in P, e poi considero le altre tangenti vicino a P che formeranno un certo angolo θ; più l'arco Δs si avvina a P, più possiamo parlare di curvatura in un punto P. Bene possiamo definire la curvatura che chiamiamo k come limite:
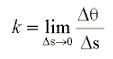
Calcolare tale limite nella realtà non è una delle cose più semplici di questo mondo. Notiamo che in ogni caso è una derivata. Quindi nella pratica dobbiamo pensare ad un definizione più agevole della curvatura.
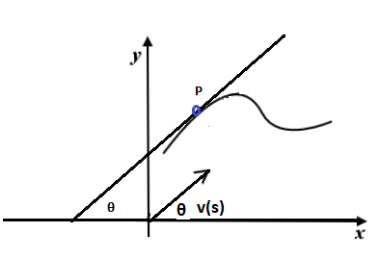
Consideriamo ancora la tangente ala curva in, ma pensiamo di traslare il vettore velocità in quel punto (che è proprio tangente alla curva) nell'origine degli assi. Consideriamo per comodità un versore, così al variare dl punto P percorrerà i punti di un cerchio unitario centrato nell'origine. Chiamiamo dunque funzione angolo θ(s) l’angolo che il versore tangente alla curva v(s) forma con la direzione fissata, ovvero l’asse delle ascisse. Si chiama curvatura (con segno) la derivata della funzione angolo rispetto al parametro arco, ovvero:
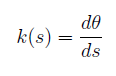
La curvatura k(s) dà la misura della velocità con cui ruota il versore tangente alla curva, una volta trasportato nell’origine degli assi (ossia sul cerchio unitario). La curvatura è altresì dotata di segno, che cambia al cambiare dell’orientazione della curva.
(questa definizione non è in conflitto con la definizione 1) ma è più comoda, per poter scrivere successivamente le equazioni riguardanti la curvatura in modo semplice. Tuttavia, nella definizione di curvatura l’angolo può essere definito a meno di una costante additiva, la cui derivata rispetto al parametro arco è ovviamente nulla.)
Partendo da questa definizione, ma noi non lo faremo, dopo una serie di calcoli tipo "forza bruta" si può dimostrare che se x(t),y(t) sono le equazioni parametriche di una curva, allora la curvatura è data dalla formula:
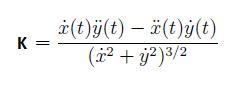
(x,e y con il punto sopra indicano la derivata rispetto al tempo di x,y; Se i punti sono due la derivata è quella seconda)
Ricaveremo invece la curvatura in un caso semplice, quello del cerchio, tanto per fare un esempio concreto;
Consideriamo una circonferenza di raggio R.
Data la perpendicolarità tra vettore tangente alla circonferenza e raggio, se φ è l’angolo descritto dal raggio sulla circonferenza, θ risulta essere pari a
![]()
2 .
Il parametro arco è
![]()
dunque si ha abbastanza immediatamente che
![]()
e di conseguenza, eseguendo la derivata rispetto a s:
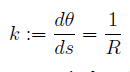
La curvatura del cerchio è dunque costante, e pari al reciproco del raggio (ossia ha una dipendenza inversa dal raggio). La proprietà di avere curvatura costante caratterizza completamente la circonferenza tra le curve del piano: si può dimostrare che ogni curva piana con curvatura costante è un arco di circonferenza. Ricordatevi però una cosa importante; questo è l'unico caso in cui una curva ha curvatura che non dipende dal punto.
Gli altri articoli di questa serie:






7 commenti
Che dire allora della terribile e usatissima Clotoide?
Cosa intendi Leandro,la clotoide o spirale di Cornu o spirale di Eulero è una curva la cui curvatura varia linearmente lungo la sua lunghezza
Cloto è la parca che tesse il filo della vita.... Beh la clotoide viene usata per progettare le curve, sia stradali che ferroviarie in modo che la curvatura sia direttamente proporzionale allo spazio percorso evitando così accelerazioni laterali .
Dite bene, Umberto e Leandro... della clotoide, per chi fosse interessato, abbiamo parlato anche in questo articolo:
http://www.infinitoteatrodelcosmo.it/2018/09/07/jerk-snap-crunkle-pop-cinquanta-sfumature-moto/
Mi fa piacere che ne parliate ; purtroppo ho introdotto le curve e lo loro curvatura solo per introdurre la curvatura di una superficie. Altrimenti avremmo potuto parlare di cose molto interessanti, tipo questa, la trattrice,o il ponte sospeso. Potremmo parlarne più avanti. Grazie.
Questa frase è molto importante....
Un conto è la traiettoria, che si chiama supporto della curva, e un conto è la curva vera e propria. Si vede subito calcolando il vettore velocità.
E già. Chissà se un giorno riuscirò a collegare questo concetto ad una curva nel piano iperbolico parametrizzata con il parametro arco che altro non è che il tempo proprio.