Categorie: Fisica classica Matematica
Tags: carta igienica conservazione massa errori misura spirale
Scritto da: Vincenzo Zappalà
Commenti:0
Srotoliamo la carta igienica (Vincenzo, Maurizio e Daniela) */**/***/****
In questo lungo articolo affrontiamo di petto il problema della carta igienica, limitando gli approcci a un numero abbastanza ristretto (se ne potrebbero tentare anche altri). Come vedremo potrebbe sembrare un problema del tutto inutile e ridicolo, ma –in fondo- oltre che a metterci di fronte a una matematica di livello crescente (e quindi molto utile per verificare le proprie conoscenze) ci può far riflettere su problematiche ben più ampie e fondamentali. Inoltre, lo reputiamo abbastanza divertente! L’articolo, iniziato da Vincenzo, ha visto la fattiva collaborazione di Daniela e Maurizio, oltre che i commenti puntuali di Umberto e Leandro. Un lavoro veramente corale che può essere letto da tutti, cosa questa che auspichiamo fortemente.
Il problema della carta igienica stava snaturandosi, arricchendosi di considerazioni che andavano troppo nel pratico, dando poco spazio a una trattazione di pura (o quasi) matematica. Conviene dare alcuni risultati ottenuti con approcci via via meno approssimati, tenendo giustamente conto che nessuno di loro sarà mai in grado di dare la lunghezza reale, ottenuta srotolando il rotolo.
Innanzitutto, ricordiamo che noi siamo partiti da dati ottenuti in modo diretto e, quindi, con tutte le incertezze insite nelle misure. Potremmo anche considerare esatto il raggio del cerchio interno attorno a cui è avvolta la carta, essendo un cilindro che possiamo ipotizzare rigido, ma già diventa più difficile misurare il cerchio esterno a causa della sua "morbidezza". Diventa ancora più difficile misurare qualcosa di estremamente sottile come lo spessore della carta. Forse ci vorrebbe un microscopio elettronico... ma ci accorgeremmo, come dicevano bene Maurizio e Oreste, che la carta è tutto meno che un foglio liscio a spessore costante. Senza entrare nei particolari, se fosse veramente liscia perderebbe molto del suo scopo.
Ogni tentativo di misura sarà, quindi, sicuramente diverso dalla misura compiuta srotolando realmente l'intero rotolo. Diciamo perciò che si ha una migliore approssimazione quando si utilizza una funzione di completezza crescente, ma che rimane, comunque, piuttosto lontana dalla realtà. Troppi parametri, più o meno variabili, si celano all'interno del rotolo che non siamo in grado di inserire, un po' come succede nelle previsioni del tempo o in climatologia.
Con queste considerazioni fatte nostre fin dall'inizio vediamo qualche metodo legato sia alla fisica che alla pura matematica (con tutti i suoi limiti).
Innanzitutto riproponiamo i dati del problema:
Raggio esterno del rotolo: R = 55 mm
Raggio interno del rotolo = raggio del cilindro di cartone su cui è avvolto: r = 20 mm
Spessore della carta: s = 0.36 mm
Ciò che vogliamo calcolare è decisamente semplice (a parole): la lunghezza L del rotolo di carta igienica.
Non pretendiamo un numero esatto, dato che i parametri sono stati determinati a... rotolo chiuso.
Conservazione della massa
Diciamo subito che il metodo fisico è -probabilmente- il più veritiero, anche se sembra disinteressarsi del tutto del modo con cui è arrotolata la carta. In pratica esso ci dice che, srotolata oppure no, la carta è sempre la stessa e, come tale, deve conservare la massa.
Basta perciò calcolare la massa del rotolo e uguagliarla con la massa del lungo foglio completamente srotolato. La densità della carta è assunta costante e a maggior ragione sarà la stessa prima e dopo lo srotolamento. Invece della massa, perciò, possiamo usare direttamente il volume (e ricadiamo nell'approccio fornitoci da Umberto).
In pratica, abbiamo un volume compreso tra due cilindri e un volume fornitoci da un cuboide rettangolo estremamente sottile.
Non vi è nemmeno bisogno di ragionare in termini di volume, dato che sia la carta arrotolata che quella srotolata mantengono una certa larghezza d. Per cui è sufficiente lavorare su una differenza di aree (le sezioni perpendicolari al rotoli). La prima area è la differenza tra l'area del cerchio di raggio R e quello di raggio r, mentre la seconda è quella del rettangolo di lunghezza L e di altezza s.
Possiamo scrivere:
π(R2 - r2) = L s
da cui:
L = π(R2 - r2)/s
Nel nostro caso otteniamo (assumendo sempre π = 3.1416)
L = 3.1416 (552 - 202)/0.36 = 22907.50 mm
Il metodo appena descritto è decisamente il più semplice e il più diretto ed è quello a cui fa riferimento anche Leandro.

La fisica spesso ha bisogno di poca matematica per esprimersi al meglio. Spesso e volentieri, formule troppo complicate per descrivere un fenomeno sono legate alla nostra incapacità di determinare la giusta legge che lo governa. La matematica è un linguaggio e come tale, a volte, si complica inutilmente. Non sapendo una certa parola in una lingua straniera, si cerca, spesso, di fare un giro di parole sovrabbondanti per cercare di ottenere lo stesso significato. Stiamo quindi sempre attenti a non dare alla matematica un ruolo troppo fondamentale nello studio dell'Universo in generale. Lo stesso Einstein, genio assoluto nella visione fisica, ha dovuto attingere al serbatoio già esistente della matematica per riuscire a descrivere la sua intuizione. Niente toglie, però, che il linguaggio matematico venga studiato di per sé, anche senza reali possibilità di applicazioni fisiche. D'altra parte c'è chi studia un linguaggio antico o moderno in cerca di tutte le sue sfumature. Prima o poi, arriverà uno Shakespeare a caso che sa come usarlo!
Passiamo, perciò, alla geometria e alle formule matematiche, partendo dal caso più semplice e decisamente approssimato.
Cerchi concentrici
Questo metodo adotta la soluzione più ovvia: ogni giro della carta attorno al cilindro interno è considerato a sé stante. Qualcosa come quanto illustrato in Fig. 1

Ovviamente il primo strato circolare deve coincidere nella sua parte interna con il cilindro di base. Avendo, però, uno spessore s, la sua lunghezza “esterna” differisce da quella “interna”. La differenza tra le due circonferenze è data da:
2π(r + s) - 2πr = 2πr + 2πs - 2πr = 2πs
Se consideriamo s << r, possiamo trascurare questo termine e assumere la circonferenza di ogni strato uguale a quella corrispondente al raggio interno. Anche visivamente si capisce che questo è il caso limite per s che tende a zero. Sicuramente è una misura per difetto, ma già in grado di dare una prima approssimazione.
In particolare, abbiamo:
1° strato R1 = r
2° strato R2 = r + s
3° strato R3 = r + 2s
………………………….
i-esimo strato Ri = r + (i - 1)s
Di conseguenza per n strati abbiamo la lunghezza totale L1 data dalle somme delle rispettive circonferenze:
L1 = 2πΣi=1n Ri = 2π Σi=1n (r + (i - 1)s) = 2π rΣi=1n 1 + 2π sΣi=1n (i - 1)
L1 = 2π r n + 2π sΣi=1n- 1 i = 2π r n + 2π s n(n-1)/2
L1 = 2π r n + π s n(n-1)
Ma il numero di avvolgimenti n si può ricavare dalla semplice relazione:
n = (R – r)/s = (55 – 20)/0.36 = 97.22
Anche n diventa un dato del problema. Avendo considerato cerchi concentrici, un numero di avvolgimenti non intero è sicuramente assurdo (diversa sarebbe la situazione se il raggio Ri crescesse continuamente …).
Ne segue che il primo calcolo, decisamente per difetto già di partenza, conviene eseguirlo considerando gli avvolgimenti pari a 97. Otteniamo:
L1 = 2 ∙ 3.1416 ∙ 20 ∙ 97 + 3.1416 ∙ 0.36 ∙ 97 ∙ 96 = 22721.06 mm
Per puro spirito matematico, possiamo anche toglierci la voglia di utilizzare un numero di avvolgimenti non intero, ben sapendo che rispecchia una soluzione che non può essere ammessa nell’approccio utilizzato:
L1’ = 22796.78 mm
La differenza è piccola e L1 resta decisamente ben al di sotto del valore ottenuto fisicamente (circa 186 mm).
Potremmo, però, pensare che la carta sia stata “schiacciata” e che il valore di R misurato sia leggermente inferiore a quello teorico. In tal caso potremmo anche usare n = 98, ottenendo un valore decisamente più grande di quello precedente:
L1” = 23066.13 mm
Ribadiamo, però, che questo valore tiene conto di un errore di partenza dovuto alle misure effettuate a “rotolo chiuso”
Lasciamo questi numeri a “bagnomaria” ripromettendoci di tornarci sopra a tempo debito. Questo approccio è quello che è stato utilizzato da Daniela, a parte l’aggiunta di uno strato in più.
Una spirale circolarizzata
La configurazione è, teoricamente, del tutto diversa da quanto ipotizzato finora. La carta deve avvolgersi attorno al cilindro di base, ma, compiuto il primo giro deve ritrovarsi sollevata di s rispetto al punto di partenza. La migliore curva che simuli questo percorso è decisamente la spirale, in cui la distanza della carta dal cerchio di partenza aumenti continuamente e costantemente. Rappresentiamola nella Fig. 2

Non vogliamo, però, affrontare ancora la lunghezza di una curva di questo tipo e, allora, torniamo al modello dei cerchi concentrici con l’avvertenza di “aggiustare” il tiro, di cerchio in cerchio (Fig 3).

Assumiamo perciò che il raggio i-esimo sia dato da una media tra il raggio considerato nel paragrafo precedente e quello a cui è stato aggiunto il valore s. In termini matematici è come se al raggio precedente aggiungessimo lo spessore s/2:
Ri’ = r + (i – 1)s + s/2 = Ri + s/2
Calcoliamo formalmente la lunghezza della carta e la chiamiamo L2
L2 = 2πΣi=1n Ri’ = 2πΣi=1n( r + (i – 1)s + s/2) = 2πΣi=1n( r + is – s + s/2) = 2πΣi=1n( r– s/2 + is)
L2 = 2πΣi=1n( r – s/2) + 2πΣi=1n i s = 2π ( r – s/2) Σi=1n 1 + 2π s Σi=1n i
L2 = 2π r n – 2π s n/2 + 2π s n(n+1)/2 = 2π r n - π s n + π s n2 + π s n
L2 = 2π r n + π s n2
Decisamente più grande di L1 (il termine aggiuntivo vede un n al quadrato e non un n moltiplicato per (n-1)), ma proviamo a inserire al posto di n il valore (R – r)/s
L2 = π n( 2r + ns)
L2 = π (R – r)(2r + (R – r))/s
L2 = π (2Rr + R(R– r) – 2r2 - r (R – r))/s
L2 = π (2Rr + R2 – Rr – 2r2 – Rr + r2)/s
L2 = π (R2 - r2)/s
Esattamente lo stesso valore che avevamo trovato con il metodo fisico!
L2 = 22907.50 mm
Possiamo anche dimostrare il perché in modo estremamente semplice…
Consideriamo una risma di fogli di spessore S e di lunghezza l. Se vi sono n fogli nella risma, possiamo subito dire che lo spessore di un singolo foglio è dato da:
s = S/n
n = S/s
La lunghezza totale della risma si ottiene appiccicando ogni foglio uno all’altro lungo il bordo, ossia:
L = l n = l S/s
Questo risultato ci dice che la lunghezza totale può essere interpretata come l’area della sezione di risma (l S) divisa per lo spessore del singolo foglio. Esattamente ciò che abbiamo fatto nel caso “fisico” (area tra i due cerchi divisa per lo spessore della carta).
Questo banale calcoletto ci potrebbe già bastare per assumere L2 come la realtà, partendo dai dati iniziali considerati esatti.
Appiccichiamo la carta
In parole povere, potremmo già fermarci qui. Tuttavia, resta ancora in ballo il fatto che noi abbiamo finora considerata la carta in grado di non lasciare alcuno spazio vuoto al suo interno. Ma questo è possibile? In realtà no, a meno di non assumere un modello come quello proposto da Maurizio con tanto di scalino… (Fig. 4)

Spiegazione della figura: Alla fine del primo giro (blu) la carta si piega e “sale il gradino”. Alla lunghezza della circonferenza si somma un tratto di lunghezza s (altezza gradino = spessore carta).
Alla fine del giro seguente, (verde) questo spazio s (blu) risulta già occupato. Quindi la lunghezza del secondo giro è data da circonferenza – s e, con il nuovo tratto in salita in cui si somma proprio s, si arriva ad una compensazione. Per tutti i giri questo meccanismo si ripete, tranne per l'ultimo che non deve salire oltre e avrà lunghezza pari alla circonferenza – s.
In conclusione l'eccesso di lunghezza del primo giro e il difetto dell'ultimo si compensano e tutto il volume risulta riempito da una striscia che ha la stessa lunghezza L2= 22907.50 mm della somma delle n circonferenze.
Questa soluzione necessiterebbe l’incollamento diretto di ogni strato su quello precedente. Un lavoro praticamente assurdo che, oltretutto, farebbe perdere alla carta igienica il suo scopo, dato che essa diventerebbe un rotolo… non srotolabile!

Incolliamo il primo giro (ma non tutto)
Più interessante è invece la soluzione in cui il primo giro di carta aderisca al cilindro interno fino a poco prima dello scalino e poi prosegua per la tangente fino a raggiungere un’altezza pari a s. In questo modo basterebbe usare la colla solo nel tratto iniziale perché nei giri successivi la carta sarebbe costretta a seguire un percorso stabilito perfettamente dal primo giro. Ci sarebbe solo un leggero rigonfiamento praticamente impercettibile. In questo modo si terrebbe conto della presenza di un piccolo spazio vuoto iniziale (Fig. 5).
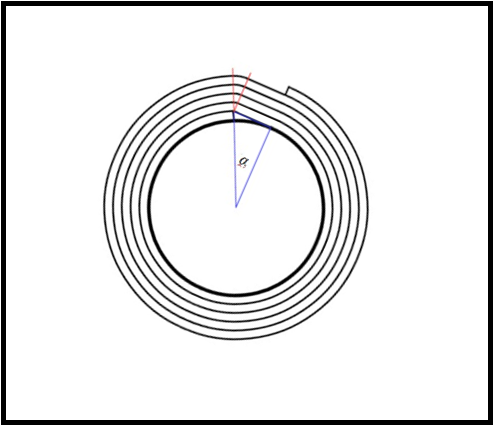
Scrive Maurizio (probabilmente copiando dal Codice Atlantico...) :
Ho immaginato che la carta venga avvolta con una certa tensione, che la tiene aderente al nucleo fino a quando incontra lo scalino. A questo punto, restando tesa , si assesta su una linea che è tangente al nucleo di cartoncino e tocca il bordo di inizio del nastro, appunto dove c'è lo scalino. Tra il punto di tangenza e lo scalino resta uno spazio vuoto (che si suppone venga occupato dall'aria , essendo risaputo che la natura trova ripugnante il vuoto). La forma del primo giro non è un cerchio perfetto ma si chiude con quel diritto segmento di lunghezza calcolabile. Il giro successivo aderisce perfettamente e mantiene la forma distorta. E così tutti gli altri giri (omotetici) che verranno.
In questo schema, è intuitivo che la lunghezza che troveremo sarà inferiore rispetto alle precedenti misure descritte.
Il percorso lungo linea tangente alla circonferenza di raggio r (che potremmo anche chiamare R1), che giunge al livello superiore (di raggio R2= r + s) è più breve del percorso che sale verticalmente da r a R2 (l'ipotenusa è per sua natura più piccola della somma dei cateti).
Avendo noi la misura dello spessore, si può calcolare l'angolo α tra punto di tangenza e gradino (Fig. 5 – Copyright Umberto – sec. XXI d.C.)
α = arcos (r/(r+s))
La lunghezza dell'arco corrispondente vale
A= r (α π/180)
Invece di seguire quell'arco, la striscia si disporrà lungo la linea di raccordo tangenziale che avrà lunghezza
T = r sen(α).
la lunghezza dell'anello di raggio r, così deformato sarà:
l1= 2 π r - A +T
La riduzione di lunghezza rispetto allo schema di L2 è data dal rapporto:
K = ( 2 π r- A -T ) / (2πr) (fattore di forma)
Dato che la deformazione si riproduce su tutti gli anelli concentrici, questo rapporto vale anche a livello globale. La lunghezza totale in questo schema è quella L2 (già trovata) moltiplicata per il fattore di forma
L3= L2 ∙ K
Passando ai valori dell'esempio: r= 20 mm s=0,36 mm
α = arcos ( 20 / 20.36) = 10,79°
A= 20 (10.79 ∙ 3.1416/180) =3.77 mm
T=20∙ sen(10.79) = 3.74 mm
l1=2 ∙3.1416 ∙ 20 – 3.77 + 3.74 = 125.63 mm (lunghezza del primo giro)
K= 125.63/125.66 = 0.9998 (fattore di forma)
Lunghezza totale = 22 907.50 ∙ 0,9998 = 22902.91mm
L3 = 22902.91 mm
Un risultato molto ambiguo in quanto abbiamo dovuto prendere quattro decimali nel fattore di forma, altrimenti avremmo ottenuto K = 1 e L3 = L2
Abbiamo usato una descrizione piuttosto empirica, ammettendo che la carta si avvolga con una curva disegnata “ad hoc”. Possiamo ottenere qualcosa di analogo, lasciando libera la carta , avendola attaccata solo nel punto d’inizio, considerato infinitesimo? E’ proprio quello che vogliamo fare, sapendo di cadere completamente nelle braccia della matematica più pura, in un mondo in cui le curve vanno descritte da una certa funzione analitica.

Una spirale perfetta
Si torna, in qualche modo, nuovamente alla spirale con raggio via via crescente. La spirale è una curva continua e trovare la sua lunghezza è un calcolo puramente analitico. Potremmo anche arrivarci con approssimazioni successive, ma tanto vale passare alla soluzione “perfetta” (in senso matematico), ricordando che stiamo tirando in ballo ancora una volta Archimede. In parole molto povere, vogliamo trovare la lunghezza della sua spirale tenendo conto dei dati iniziali del problema. Una trattazione analitica descrivibile perfettamente, anche se in modo assolutamente non semplice, che ci dà la lunghezza del rotolo sulla base perfetta dei dati di partenza e di una curva puramente teorica. Vedremo che, comunque, il risultato ben poco migliorerà nel caso pratico… Attenzione, quindi, a usare la matematica più raffinata senza avere ben presente le condizioni al contorno e lo scopo finale.
L'equazione polare della spirale è molto semplice e induce “ingannevolmente” a pensare che trovare la lunghezza di un suo arco sia una operazione veloce e priva di ostacoli. Notiamo che è stato usato r0 al posto del “vecchio” r per non confondere un valore noto con una variabile (Fig. 6).

r(ϑ) = r0 + ϑ s/2π
Relazione che si verifica immediatamente: per ϑ = 0, r = r0 ; per ϑ = 2π, r = r0 + s
Si tratta di una relazione lineare formalmente simile alla equazione cartesiana di una retta con parametro angolare (spessore) e ordinata all'origine (r iniziale).
Il raggio iniziale r0 (che va dal centro a punto A) è ovviamente il raggio del nucleo cilindrico di cartoncino. Il passo della spirale non è altro che lo spessore della carta.
L'arco BC, supposto infinitesimo, è assimilato ad un triangolo rettangolo di cateti BD e DC. Ricorrendo al teorema di Pitagora, troviamo la lunghezza della ipotenusa BC =√ (BD2 + DC2)
Ma essendo BD = r dϑ e DC = dr
dl = √ (r dϑ2 + dr2) = √(r dϑ2 + dr2 dϑ2/dϑ2) = √( (r2 + dr2/dϑ2) dϑ2) = √(r2 + dr2/dϑ2) dϑ
Quindi sotto radice appare il quadrato della funzione sommato al quadrato della sua derivata rispetto a ϑ
dl = √(r2(ϑ) + (dr/dϑ)2 dϑ
Integrando questa funzione nell'intervallo da ϑ = 0 a ϑ = 2πn (ove n è il numero di giri, ricavabile dalla differenza dei raggi interno e esterno divisa per lo spessore s) si ottiene la lunghezza dell'arco di spirale.
Con i valori dati, l'estremo superiore vale
2 ∙ 3.1416 ∙ (55 - 20)/0.36 = 610.87
Riassumendo, è nota la funzione:
r(ϑ) = r0 + ϑ s/2π
ed è nota la sua derivata
dr/dϑ = s/2π
L'integrale da calcolare è il seguente
L4 = ∫0 2πn √((r2(ϑ) + (dr/dϑ)2) dϑ
Sostituendo e sviluppando i quadrati:
L4 = ∫0 2πn √(r02 + ϑ2 s2/4π2 + r0sϑ/π + s2/4π2) dϑ
Beh… questo non è certo un integrale facile, presentando un polinomio sotto radice.
Per eseguire il calcolo conviene consultare le tavole degli integrali (la bibbia degli ingegneri), oppure un comodo "tool" online come Wolfram Alpha. Inserendo la funzione da integrare con i dati del problema e l'intervallo di integrazione il risultato che otteniamo è:
L4 = 22907.71 mm
Come potete vedere, sotto il risultato appare la domanda se si desidera avere la soluzione con tutti i passaggi espliciti. Si tratta però di un servizio a pagamento.
Il risultato conferma che questo è il modello che dà la misura più lunga. Una rozza approssimazione (in parte disegnata a mano libera) tra L2, L3 e L4 si vede nella Fig. 7, dalla quale prendiamo spunto per proporvi una generalizzazione.

Sappiamo che tra due figure, ad esempio due triangoli rettangoli , esiste una similitudine quando il rapporto tra i lati è costante, ha un valore che chiameremo K.
Il rapporto tra le ipotenuse avrà il medesimo valore K di quello tra i due cateti maggiori e di quello tra i due cateti minori.
Se, oltre ad avere questo rapporto di similitudine, l'orientamento delle due figure è il medesimo ( ad esempio le due ipotenuse giacciono su una medesima retta) allora le due figure sono “omotetiche”. In questo caso possiamo infilare il triangolo più piccolo in quello più grande, come potete facilmente visualizzare anche senza un disegno.
Due anelli concentrici, a contatto sono figure omotetiche. Tra i loro raggi esiste un rapporto K. Ma anche nel caso di due ellissi concentriche a contatto possiamo parlare di omotetia.
Pensando ai nostri modelli, ridisegnati nella figura soprastante, possiamo riconoscere questa particolarità: esiste una figura interna, il primo giro di carta, che detta la legge a tutte le altre, Imprime una forma particolare che viene replicata strato do po strato, sempre identica.
In questa tassellatura, ciascun elemento è più grande del precedente del rapporto k= (1+s). La seconda spira è grande k volte la prima. Il fattore di ingrandimento agisce linearmente sulla lunghezza. Proprio come succede per le ipotenuse dei due triangoli simili.
La somma di tutte le lunghezze porta alla lunghezza complessiva. Naturalmente nei primi due modelli, “rampa” e scalino” il calcolo della spira viene fatto con semplici calcoli geometrici (l'integrale di un arco di circonferenza è immediato) mentre nel caso della spirale occorre proprio fare i conti con l'integrazione della funzione.
A questo punto potreste pensare di togliervi la curiosità procedendo autonomamente al calcolo manuale di questo “semplice integrale”.
Ma fermatevi un attimo a riflettere, perché la ricerca della primitiva di un integrale richiede la capacità di riconoscere la fisionomia, ossia la struttura, della funzione integranda, per poter applicare il metodo più adatto al particolare caso. Una vera arte, che richiede applicazione ed esercizio, per poter sviluppare la adeguata sensibilità. L' individuazione di una sostituzione di variabile efficace, (come, in generale, la scelta del sistema di riferimento più conveniente per esprimere una relazione matematica o fisica), porta a semplificazioni determinanti per arrivare alla soluzione.
Esistono alcuni metodi con cui si possono affrontare anche integrali particolarmente complicati, come quelli di funzioni irrazionali.
In particolare, nel caso di una funzione espressa da un radicando contenete un trinomio di secondo grado – proprio il nostro caso - esiste un metodo di “sostituzione della variabile”, denominato sostituzione di Eulero (tanto per cambiare), che rappresenta lo strumento classico di risoluzione.
Per questo tipo di problemi consigliamo vivamente questo testo che si trova gratis sul web.
Lo scopo è di trasformare l'integrale irrazionale in integrale razionale e di procedere poi con il metodo dei fratti semplici, quello più comunemente usato per funzioni razionali fratte.
Avrete capito che il percorso non è poi così lineare, anche per il fatto che la divisione polinomiale, pur essendo una operazione del tutto meccanica e ripetitiva, è spesso fonte di banali errori che compromettono il raggiungimento del risultato, nel nostro caso la consapevolezza di quanto è lunga questa benedetta striscia di carta igienica.
Riflessioni conclusive
Ci siamo sicuramente divertiti nel cercare di adottare il sistema migliore per conoscere “a priori” la lunghezza della carta igienica. Ripetiamo, però, che siamo partiti da dati misurati direttamente che comportano degli errori intrinsechi, in parte dovuti allo strumento di misura e in parte alle deformazioni non modellabili del rotolo di carta. E’ un po’ come quando si osserva una galassia e poi si cerca di descrivere compiutamente un certo fenomeno. La descrizione può anche essere esatta, ma i dati osservativi non permettono di confermare in pieno il modello ultra sofisticato. A quel punto, ci chiediamo:
“E’ proprio necessario creare un modello matematico che non potrà mai essere provato osservativamente? Non sarebbe forse meglio adottare un modello semplificato che corrisponda alla precisione ottenibile?”.
La risposta non è facile e -forse- non esiste nemmeno. Se Einstein non avesse elaborato una trattazione ultra particolareggiata, certi fenomeni del tutto sconosciuti e imprevedibili non si sarebbero mai scoperti o sarebbero rimasti nel campo dei “misteri” irrisolti del Cosmo. In poche parole, bisognerebbe usare una via di mezzo, un compromesso stabilito con grande razionalità ed esperienza. Spesso e volentieri questo non è fatto…
La nostra carta igienica ce lo dimostra. Noi abbiamo accettato un valore di 0.36 mm per lo spessore ben sapendo che una tale precisione è del tutto aleatoria e può essere facilmente distrutta da fattori non preventivabili esistenti nell’avvolgimento e nell’impacchettamento o quello che è. Ma lo stesso può capitare per il diametro esterno e andare a calcolare un minimo, giustamente ipotizzabile, vuoto interno diventa una sottigliezza quasi ridicola, pari al voler calcolare al metro la distanza di una galassia lontana…
Inoltre, siamo partiti dai centesimi di millimetro per lo spessore, ma abbiamo assunto il millimetro come ultima cifra significativa dei raggi. Come se non bastasse, abbiamo scelto il pi greco con quattro decimali dopo la virgola. Insomma, per cercare di mantenere una certa regolarità, abbiamo introdotto una serie di approssimazioni di calcolo non perfettamente ammissibili. Gli stessi risultati sono stati dati in modo alquanto arbitrario, decidendo le due cifre decimali solo per essere in sintonia con le due cifre decimali dello spessore. Insomma, una strategia operativa non certo ineccepibile. Tuttavia, il succo era quello di paragonare tra loro vari approcci e non veramente risolvere il “quiz”.
A riprova di tutto ciò, riportiamo la misura reale del rotolo di carta igienica una volta srotolato:
Lreale = 23200 mm
Un valore decisamente superiore a quello di tutti i nostri tentativi scelti con crescente ricerca di perfezione matematica. Il valore più vicino è in fondo L1” ottenuto proprio ammettendo una piccola assurdità matematica …
Il caso proposto è stato veramente eseguito in un Istituto universitario americano e quindi il risultato finale è fortemente dipendente da quel rotolo, da quelle condizioni e dagli strumenti di misura usati. Se lo rifacessimo noi troveremmo sicuramente un valore reale decisamente diverso.
Insomma, la matematica troppo spinta non serve a niente?
No, assolutamente no, ma andrebbe sempre usata con grande attenzione a tutte le condizioni al contorno e questo vale sia il nostro rotolo di carta igienica che per la misura degli ammassi galattici. In fondo, in fondo…- e mi spiace dirlo- a volte gli ingegneri sono più razionali e concreti, anche se la relatività generale non l’avrebbero mai presa in considerazione.
Lungi da noi qualsiasi polemica, proprio perché siamo ben consci del valore di ogni approccio scientifico corredato da grande sapienza pratica (il ponte di San Francisco ne è una prova fantastica).
Conclusione conclusiva
Parliamoci chiaro, in certi momenti non sono certo pochi millimetri a risolvere una situazione critica e potremmo concludere con una massima di Maurizio: “Non curatevi di quanto è lunga, ma non fatevela mai mancare…”.
Senza esagerare, però... ![]()

Appendice relativa al calcolo della lunghezza dell'arco di spirale di Archimede (Mauritius docet...)
Parlando di integrazione, in termini generali, si era detto che:
L' individuazione di una sostituzione di variabile efficace, (come, in generale, la scelta del sistema di riferimento più conveniente per esprimere una relazione matematica o fisica), porta a semplificazioni determinanti per arrivare alla soluzione.
E' proprio quella frase "sistema di riferimento più conveniente" che può aprire la via ad un modo diverso di calcolare la lunghezza del rotolo di carta, le cui benemerenze sono state così dottamente illustrate da Daniela a suon di pillole.
La scelta del punto di origine della spirale era inizialmente caduta sul punto di incollatura al nucleo, perché era proprio da lì che iniziava ad avvolgersi il nastro. Ma se ragionassimo diversamente? Se dicessimo, ad esempio, che la spirale matematica ha la sua origine nel centro del nucleo e si sviluppa (in astratto) fino a quando il suo raggio giunge al valore di 20 mm e solo da lì inizia a conquistare una evidenza materica, si fa carta, mentre prima era solo una fantomatica traiettoria? E da lì , fino alla fine , fin quando il raggio assume trionfalmente il valore di 55 mm, prosegue nella sua solida, rassicurante e carezzevole consistenza? Ebbene, diciamolo.
L'equazione della spirale che parte dal centro è certo più semplice, il valore del suo raggio iniziale è nullo. Guardate che bella è ...
r(ϑ) = ϑ s/2π
Vuol dire che i limiti di integrazione per calcolare la lunghezza "utile" andranno da 2π · 20/0.36 a 2π · 55/0.36 tenendo conto che, nel momento in cui inizia la striscia, la curva ha già compiuto una serie di giri, un percorso che l' ha condotta, radiante dopo radiante, ad avere lo stesso raggio del nucleo.

La lunghezza dell'arco , con questa amichevole equazione, la calcoleremo come integrale della radice di un binomio, non di un trinomio, come era prima... Come diceva un noto personaggio politico

Possiamo farcela a calcolare questo integrale !
o, se preferite,
Abbiamo recentemente visto che per le funzioni iperboliche vale una curiosa relazione, questa: cosh2 t - senh2 t= 1
come dire che:
noterete che questa radice ha la stessa struttura di quella sotto integrale. Basta porre
Calcoliamo anche il differenziale ossia
(la derivata di cosh t è senh t e viceversa..... che meraviglia.)
e ora riscriviamo l'integrale con questa nuova variabile t.
e integrando ...
( * )
possiamo riportarci alla variabile di origine
La relazione esistente tra t e è questa: senh t =
come dire che
et- e-t = 2
da cui, moltiplicando a sinistra e destra per si ha:
equazione di secondo grado da cui ricavare
da cui , scegliendo necessariamente il segno + otteniamo
e quindi:
che andremo a sostituire nel risultato della integrazione. ( * )
=
resta solo da eseguire il calcolo in corrispondenza ai limiti dell'intervallo e fare la differenza e,
con l'aiuto di Excel, otteniamo agevolmente il nostro obiettivo.
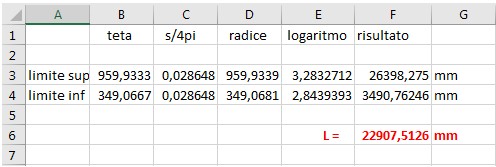
Sembra proprio che il risultato confermi quanto abbondantemente ottenuto in precedenza.
E' bastato scegliere il sistema di riferimento più semplice.







