Questo articolo è stato inserito nella pagina d'archivio dedicata alla Disuguaglianza di Bell

LA DISUGUAGLIANZA DI BELL
Riprendiamo il discorso

Riprendo qui il discorso sulla disuguaglianza di Bell iniziato con questo articolo introduttivo. È passato molto tempo, ma spero che l’argomento continui ad interessare.

Come gli altri articoli che ho scritto, anche questo è solo una racconto agli amici del Circolo delle letture su argomenti che penso siano di interesse comune ai frequentatori del Circolo e che mi hanno particolarmente appassionato e meravigliato. Non è certo un trasferimento di informazioni e nozioni, delle quali non mi sento depositario, ma mi piacerebbe fosse l'avvio di un dialogo come una volte si faceva nei circoli davanti ad un caffè o un aperitivo.

Prima di iniziare riprendo quanto detto nel precedente articolo introduttivo.

I risultati della meccanica quantistica sono spesso sorprendenti per la nostra abituale percezione del mondo. Fin dall'inizio della sua storia, i fisici hanno molto discusso su come interpretarli. L'interpretazione che si è consolidata è stata quella promossa dal grande fisico danese Niels Bohr con il contributo di altri grandi fisici come, tra gli altri, Max Born. Questa interpretazione è denominata in vario modo, nel seguito la indicherò come interpretazione standard. L'interpretazione standard è sicuramente una teoria di grande successo. Ha permesso di fare previsioni sul comportamento della natura verificate sperimentalmente con ottima precisione. Pressoché nessuno dubita che sia corretta, per quanto possa essere considerata corretta una teoria scientifica.

Ciò nonostante, ci sono alcuni elementi sui quali si fonda questa interpretazione, e la descrizione del mondo che ne deriva, che sono stati giudicati insoddisfacenti da alcuni importanti fisici.

Forse l'aspetto più rilevante riguarda la realtà del mondo esterno a noi. L'interpretazione standard rinuncia all'esistenza di una realtà esterna con proprietà definite, indipendenti dalla presenza di qualcuno (o qualcosa) che la stia osservando.

Qui di seguito ci sono alcune posizioni di importanti fisici sull'argomento. La perplessità di Albert Einstein è sintetizzata in una delle sue frasi celebri. “Credi veramente che la Luna esista solo quando la guardo?”. Anche Richard Feynman ha esercitato il suo spirito sull'argomento: “Ritieni seriamente che senza un osservatore non ci sia una realtà? Chi è l'osservatore? Una mosca..[.]..Una stella..[.]..Oppure sei tu l'osservatore? Allora ci sarà qualche realtà per il mondo dopo che sarai morto? Conosco un certo numero di fisici rispettabili che hanno stipulato un'assicurazione sulla vita.”. Per completare il panorama con un contemporaneo, cito anche Roger Penrose: “Abbiamo bisogno di un concetto di realtà fisica, per quanto approssimato e provvisorio, perché senza di esso il nostro universo oggettivo, e quindi tutta la scienza, semplicemente evapora davanti al nostro sguardo contemplativo!” Scienziati di tre generazioni dei quali non si può dubitare della loro profonda conoscenza della fisica. Per contro ci sono altri fisici importanti che hanno accettato senza conflitti la posizione di Niels Bohr o comunque hanno ritenuto il problema non rilevante. Alle volte uno stesso fisico ha assunto posizioni con diverse sfumature in diversi interventi. Per evitare fraintendimenti, occorre chiarire che nessun fisico ha comunque avuto mai dubbi sulla capacità predittiva del formalismo della interpretazione standard della Meccanica Quantistica. I box di questo colore racchiudono alcune note sul testo

Un altro aspetto che ha generato perplessità è la necessità di prevedere che in alcuni casi ci sia una azione a distanza istantanea tra due particelle remote. Questa azione modifica lo stato di una delle particelle senza che la particella abbia interazioni con alcunché. L'esito della variazione di stato dipende dall'esito della variazione di stato di un'altra particella remota. Questo avviene indipendentemente dalla distanza tra le due particelle.

Einstein la chiamò "spukhafte Fernwirkung". Tra le traduzioni che ho visto, quella che preferisco è “inquietante azione a distanza”, anche se forse non è la più corretta.

In sintesi l'interpretazione standard è una teoria non realista e non locale.

Albert Einstein, insieme ai suoi collaboratori Podolsky e Rosen, mise in evidenza questi aspetti, per lui critici, della interpretazione standard in un celebre articolo del 1935. Auspicò la ricerca di una teoria corretta, cioè che producesse i medesimi risultati della interpretazione standard, ma realista e locale.

John Stewart Bell si domandò se fosse possibile immaginare una interpretazione alternativa alla interpretazione standard che facesse a meno di questa "spukhafte Fernwirkung". Una teoria che possiamo indicare come locale, cioè senza azioni a distanza.

J.S.Bell scoprì che una qualsiasi teoria locale, cioè senza effetti istantanei a distanza, in alcuni particolari casi non può dare le stesse previsioni della interpretazione standard. Quindi un teoria locale, comunque formulata, non può essere totalmente equivalente alla interpretazione standard.

John Stewart Bell dimostrò che il valore di una grandezza da lui individuata sarebbe stato compreso in un preciso intervallo se valutata con una qualsiasi teoria locale. In termini matematici questa affermazione si traduce in una diseguaglianza. Se chiamiamo S questa grandezza, la diseguaglianza sarà del tipo S min ≤S≤S max . Per contro, la stessa grandezza valutata con l’interpretazione standard assume un preciso valore che non è nell’intervallo definito dalla disuguaglianza di Bell.

Poiché la grandezza S è misurabile, allora si può verificare sperimentalmente quale delle due teorie non è corretta.

Le verifiche sperimentali indicano largamente che sono le teorie locali a non essere in grado di prevedere correttamente il risultato della misura. La non località sembra essere un ingrediente del quale non si può fare a meno.

A questo punto spero vi sia venuta la curiosità di sapere cosa è questa grandezza che ci permette di arrivare a questa conclusione e con quale meccanismo riesce a sondare la Natura così profondamente.

In realtà i fisici hanno individuato più di una grandezza che ci può dare questa possibilità. La maggior parte è basata sul meccanismo individuato da Bell che impiega misure su coppie di particelle entangled. Nel seguito cercherò di illustrare la disuguaglianza di Bell utilizzando una di queste grandezze ottenibile da misure sulla polarizzazione di coppie di fotoni entangled. La grandezza che vedremo è tra le più semplici da trattare. Per contro, è meno stringente ed il suo campo di applicazione è più ridotto di quello di altre, ma sufficiente per capire il meccanismo con il quale opera la disuguaglianza di Bell. Alain Aspect, il fisico sperimentale che più di altri ha contribuito alla realizzazione degli esperimenti con coppie di fotoni, ha basato alcuni suoi esperimenti su questa grandezza e l'ha descritta in alcuni suoi scritti.

Bene, iniziamo vedendo alcuni fenomeni legati alla polarizzazione del singolo fotone. Poi passeremo a quelli che interessano coppie di fotoni. Consideriamo la polarizzazione come una proprietà misurabile di ciascun fotone.

La polarizzazione può essere anche trattata come fenomeno macroscopico legato alle oscillazioni del campo elettro-magnetico come fatto in questo articolo. A noi però interessano le proprietà quantistiche della polarizzazione e quindi non seguiremo questo approccio.

Polarizzazione di fotoni singoli

La polarizzazione è una proprietà di ciascun fotone che può essere caratterizzata da una direzione, la direzione di polarizzazione. Questa direzione è perpendicolare al percorso dei fotoni.

Rappresentazione grafica di un flusso di fotoni ciascuno con la propria polarizzazione perpendicolare alla direzione di propagazione. Ovviamente non è una rappresentazione realistica.

Figura 1.1

La polarizzazione dei fotoni dei quali parleremo è una polarizzazione detta lineare. Per arrivare alla disuguaglianza di Bell è sufficiente questo tipo di polarizzazione. Quindi evito di parlare di altri tipi di polarizzazione inutilmente più complessi per il nostro scopo.

Per cercare le caratteristiche di questa proprietà occorre trovare un qualche sistema fisico che la evidenzi. La natura e la tecnologia ci offrono alcuni strumenti per farlo.

I più noti sono le lastre polarizzatrici, con le quali sono fatti gli occhiali polaroid.

Ci sono anche degli strumenti realizzati utilizzando particolari cristalli opportunamente lavorati. Immaginiamo un esperimento con uno di questi cristalli. Facciamo arrivare sul cristallo una sequenza di fotoni da una particolare traiettoria. Inseriamo uno schermo nel lato opposto del cristallo. Sullo schermo si vedrebbero due aree distinte illuminate dai fotoni passati per il cristallo. Nella figura sotto c'è una schematizzazione del fenomeno.

Figura 1.2

I fisici hanno determinato che i fotoni che producono ciascuna delle due aree hanno una diversa polarizzazione. Per arrivare a questo risultato occorrerebbe fare una serie di misure introducendo dei filtri sulle potenziali traiettorie dei fotoni. Per andare avanti più velocemente e visualizzare graficamente queste polarizzazioni, immagino un contatore di fotoni che possa anche visualizzare la polarizzazione dei fotoni conteggiati in forma di una specie di ologramma.

Posizionando due di questi immaginari contatori in corrispondenza delle due aree illuminate vedrei qualcosa di simile alla figura sotto.

Figura 1.3

In breve, possiamo dire che tutti i fotoni rivelati su uno stesso contatore hanno la stessa direzione di polarizzazione. Quindi i fotoni vengono trovati con due possibili direzioni di polarizzazione una per ciascun contatore. Le due direzioni di polarizzazione sono perpendicolari tra loro.

Vediamo nelle figura successiva come queste direzioni di polarizzazione seguono l’orientamento del cristallo.

Figura 1.4

Se il cristallo viene ruotato, le direzioni di polarizzazione dei fotoni rivelati dai contatori seguono la rotazione. È importante anche notare che queste direzioni non dipendono dalla polarizzazione dei fotoni entranti. In questo caso i fotoni entranti hanno una polarizzazione casuale.

Notate che il polarizzatore non opera una selezione, non è un “setaccio” che fa passare i fotoni entranti solo se polarizzati in una delle due direzioni perpendicolari. Il numero totale di fotoni uscenti è uguale a quello dei fotoni entranti, almeno immaginando uno strumento di misura ideale che riveli tutti i fotoni. Quindi molti di questi fotoni al passaggio nel cristallo hanno cambiato la loro polarizzazione.

I box di questo colore evidenziano le informazioni che ci serviranno in seguito.

I fotoni che transitano in un cristallo polarizzante assumono particolari proprietà di polarizzazione e posizione. I fotoni vengono rivelati da contatori posti su due diverse traiettorie. I fotoni rivelati dal medesimo contatore hanno la stessa direzione di polarizzazione. La direzione di polarizzazione dei fotoni rivelati da un contatore è perpendicolare a quella dei fotoni rivelati sull'altro contatore. Le direzioni di polarizzazione dei fotoni rivelati dipendono dall’orientamento del cristallo, ma non dipendono dalla direzione di polarizzazione dei fotoni entranti. Il numero di fotoni rivelati in uscita è, idealmente, uguale a quello dei fotoni entranti.

Le possibili direzioni di polarizzazione dei fotoni transitati nel cristallo non dipendono dalla loro polarizzazione all'ingresso del cristallo. Invece, il numero di fotoni rivelati da ciascun contatore, quindi con ciascuna delle possibili polarizzazioni uscenti, dipende dalla polarizzazione dei fotoni entranti.

Finora abbiamo utilizzato fotoni entranti polarizzati in modo equamente casuale. In modo altrettanto equamente casuale vengono rivelati dai due contatori.

Per arrivare a valutare l’effetto della disuguaglianza di Bell occorre sapere quale è la frazione di fotoni che troviamo su ciascun contatore nel caso i fotoni in ingresso abbiano una direzione di polarizzazione definita.

Lo vederemo nel prossima volta.

A questo articolo seguiranno altri cinque articoli. Il prossimo completa i fatti sperimentali riguardanti la polarizzazione dei fotoni che sono spiegati dalle teorie che vengono messe a confronto dalla disuguaglianza di Bell. Seguiranno due articoli su come l'interpretazione standard spiega alcuni effetti della polarizzazione dei fotoni che in parte abbiamo già visto in questo articolo. Il primo introduce l'argomento con i fotoni singoli ed il secondo tratta coppie di fotoni entangled, che sono l'oggetto della disuguaglianza di Bell. In questi due articoli incontreremo alcuni dei principi base della interpretazione standard.

Il quinto articolo della serie introduce la grandezza oggetto della disuguaglianza di Bell.

Nell'ultimo articolo vedremo come una teoria locale, che rinuncia a quella "spukhafte Fernwirkung" (inquietante azione a distanza), potrebbe essere costruita e quali sono i suoi inevitabili limiti individuati da Bell con la sua disuguaglianza.

La matematica necessaria per seguire questo percorso si limita all'algebra elementare, a qualche nozione base di trigonometria e a poche nozioni sui vettori. Solo nell'ultimo articolo prevedo di inserire una appendice dove ci sarà qualche integrale. Questa appendice è solo un approfondimento per chi vorrà seguirlo.

Le nozioni di trigonometria e sui vettori credo siano note a molti di coloro che seguono questo circolo. Comunque ho inserito qui di seguito una appendice con un richiamo di trigonometria per chi pensa di averne bisogno. Nel prossimo articolo ci sarà una appendice simile riguardante i vettori.

I box verdi segnalano i richiami della matematica che ci serve per arrivare a capire le implicazioni della disuguaglianza di Bell. Ovviamente non sono necessari per chi ha già dimestichezza con gli aspetti della matematica che sono trattai al loro interno.

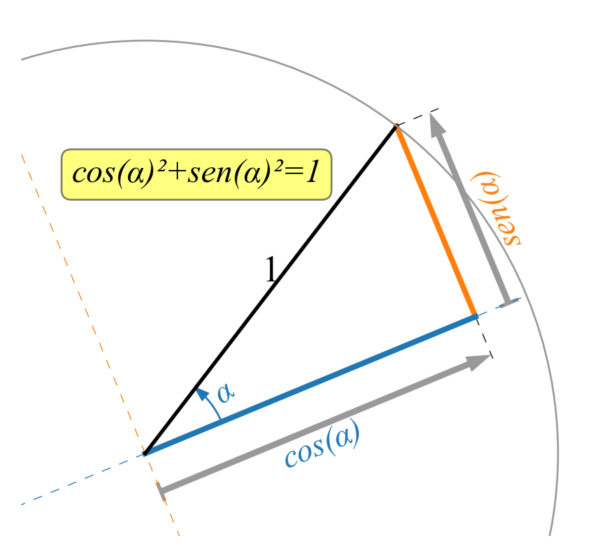
Le poche cose di trigonometria da ricordare Le definizioni Consideriamo un triangolo rettangolo di ipotenusa di lunghezza 1. La lunghezza del cateto adiacente è proprio il coseno dell’angolo, cos(α). Per non fare discriminazione è stato dato un nome anche alla lunghezza del cateto opposto all’angolo. Si chiama seno dell’angolo, sen(α). Figura 1A.1 Il triangolo rettangolo che ho disegnato sopra è ruotato rispetto alla usuale rappresentazione con il coseno in posizione orizzontale e il seno in posizione verticale. Spero che aiuti ricordare quale è il coseno e quale è il seno di un angolo indipendentemente dalla rotazione del triangolo. Prima identità importante Parlando di cateti ed ipotenusa di un triangolo rettangolo viene in mente il teorema di Pitagora. Nel triangolo che abbiamo preso per definire il coseno, la lunghezza della ipotenusa è 1 ed i cateti sono coseno e seno. Ma allora il teorema di Pitagora per questo triangolo è cos(α)²+sen(α)²=1, che ci da una importante identità che lega seno e coseno di un angolo. Estendiamo la definizione Nella figura precedente l’arco che rappresenta l’angolo e i segmenti che rappresentano il coseno e seno sono disegnati come frecce. L’arco termina con una freccia dalla parte dell’ipotenusa. Questo sta ad indicare che l’angolo è orientato in quel verso. Convenzionalmente, se la freccia è in senso antiorario l’angolo è positivo, se è in senso orario l’angolo è negativo. Nella figura seguente c’è un esempio di due angoli opposti. Figura 1A.2 I valori del seno dei due angoli sono opposti, come indicato dal verso delle frecce in figura. I valori delle coseno dei due angoli sono invece uguali. Il verso della freccia, non disegnato nella figura, è lo stesso. Quando l’angolo è maggiore di 90° il triangolo rettangolo si deve costruire diversamente. Figura 1A.3 Questa volta è esterno all’angolo, come si vede in figura sopra per l’angolo β. Il coseno è sempre pari alla lunghezza del cateto più vicino all’angolo, ma questa volta è negativo. Il seno dell’angolo β è ancora la lunghezza dell’altro cateto ed è positivo. Anche in questo caso i due segni sono fissati dai versi delle frecce. Nei due casi precedenti gli angoli messi a confronto hanno lo stesso asse di riferimento, quello azzurro. Ci troveremo a dover considerare anche angoli che partono da un riferimento diverso come nel prossimo esempio. Il primo angolo ha il solito riferimento, l'asse azzurro. Il secondo angolo ha un riferimento ruotato di 90° rispetto al precedente, l’asse arancione. Figura 1A.4 Con considerazioni simili a quelle fatte nei due casi precedenti si può trovare che valgono le relazioni indicate nella figura. Qui il teorema di Pitagora ci porta ad una relazione dove appaiono i quadrati dei coseni dei due angoli. Tutti qui quello che ci serve della trigonometria. Ovviamente non serve ricordare a memoria queste relazioni. Avremo occasione di incontrarle nuovamente. Per una spiegazione più estesa della funzione coseno e delle altre funzioni trigonometriche c'è questo articolo.

Per ora è tutto, arrivederci alla prossima.

Fabrizio Panaioli 2020