Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Chi non conosce Tarzan, l'uomo della giungla? Su di lui sono stati scritti libri, girati film e serie televisive. Ma, la versione che ci danno di lui è quella vera? Per saperne qualcosa di più è meglio rivolgersi al suo grande Maestro Citoon, considerato il più preparato e saggio tra gli insegnanti della più prestigiosa Scuola Superiore per primati di tutta l'Africa. Se contattato nel modo e al momento giusto potrebbe raccontarci qualche brano vero della vita di Tarzan. Noi abbiamo avuto questa fortuna... Per riuscire a ricostruire l'intera storia  devo ringraziare di vero cuore Citoon e l'aiuto insostituibile di Maurizio, che si è tenuta tutta per sé l'ultima parte, quella più "pratica", da vero ingegnere!

Tarzan, soddisfazione e disperazione del grande Citoon. Se eccelleva sicuramente in Educazione Fisica, non era altrettanto preparato in Fisica e Matematica. Bastava poco per metterlo in imbarazzo. Non per niente, diventato adulto, era stata a messa al suo fianco quella mente brillante di Cita, sempre pronta ad aiutarlo a risolvere gli enormi problemi che una foresta e i suoi abitanti ponevano quasi quotidianamente al nostro "eroe". Senza Cita, Tarzan diventava improvvisamente pauroso e disorientato e la sua forza fisica poteva fare ben poco per toglierlo dagli impacci. Esemplare, a questo riguardo, è l'avventura che Citoon ci ha raccontato, dopo lunghe insistenze e tanti caschi di banane di prima scelta. La possiamo intitolare: "Tarzan e il coccodrillo".

Tutto ebbe inizio un giorno in cui Cita era dovuta andare a trovare una vecchia zia molto malata e depressa. Aveva lasciato Tarzan su un pianoro roccioso, lontano da pericoli immediati, in posizione dominante sia per vedere, sia per essere visto. Poi lo aveva lasciato solo con non poca ansietà. Erano passate poche ore dalla partenza di Cita ed ecco che dalla foresta che si stendeva sulle pianure e sui monti davanti a lui si ode benissimo un grido di aiuto da parte di un gorilla dei monti Virunga. Tarzan non sa cosa fare, ma alla fine il suo animo buono e la spavalderia datagli dalla sua forza fisica, lo convince a correre in aiuto del malcapitato.

Tarzan scende a grande velocità attraverso rocce e roccette e i primi tratti di foresta fino a che non gli si para davanti un fiume limaccioso. Il che sarebbe niente per un grande nuotatore come Tarzan, ma il guaio è che dentro quelle acque, apparentemente inoffensive, si vede benissimo la testa di un enorme coccodrillo che sembra molto affamato. Le dimensioni e la forza di quell'animale sono troppo anche per Tarzan che si deve fermare e riflettere (poveri noi!).

La prima idea che gli viene in mente è quella di cercare di saltare letteralmente al di là del fiume che, stima, essere largo F metri. purtroppo, però, la conformazione delle sponde non gli permette di poter prendere una rincorsa e deve tentate il salto da fermo. Ce la può fare? Beh... anche se un po' limitato nella trattazione della fisica applicata, Tarzan si ricorda dei vecchi insegnamenti di Citoon e di come lui aveva sempre primeggiato nel lancio della pietra. In fondo, adesso la "pietra" era lui stesso e doveva solo calcolare se con la velocità che era in grado di ottenere nel salto avrebbe potuto raggiungere la sponda opposta. Si ricordava anche qualcosa su un certo angolo con il quale avrebbe superato la massima distanza possibile. La Fig. 1 rappresenta la situazione del nostro eroe e quantifica, schematizzando, i parametri fondamentali.

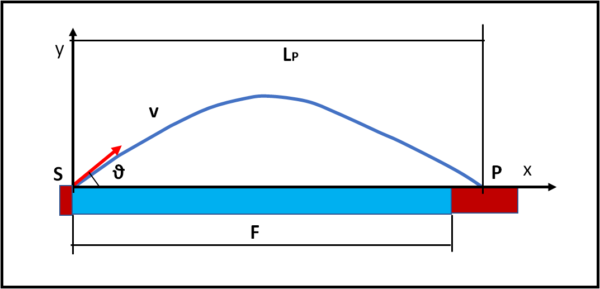
La larghezza del fiume è F. Tarzan al momento del salto si trova in S. v è la sua velocità e θ è l'angolo che deve scegliere per ottimizzare il suo salto. Tarzan scrive qualcosa sulla sabbia cercando di ricavare l'angolo migliore. Di seguito il ragionamento fatto da Tarzan.

Tarzan e il salto parabolico

Tarzan sceglie, come origine degli assi x e y, proprio la sua posizione iniziale S.

In poche parole, deve affrontare  il moto parabolico più semplice, quello che ha sempre utilizzato per descrivere il moto di un proiettile. Solo che adesso il proiettile è lui stesso! Questo argomento fa parte della meccanica più classica e studiata anche da Tarzan con discreto profitto (grazie al libro "La Fisica addormentata nella giungla", la cui "paternità" si perde nella notte dei tempi, ma che la tradizione attribuisce al leggendario TarZap).  Il punto essenziale di questo moto è che il punto di partenza S e quello di arrivo P si trovino alla stessa altezza.

E' come se Tarzan diventasse un "uomo cannone" e venisse sparato verso l'alto con una certa velocità e con un certo angolo di alzo del cannone. L'uomo scimmia si chiede: "Qual è la distanza massima percorribile e a quale angolo corrisponde?"

Il moto parabolico è composto da due moti distinti: uno orizzontale a velocità costante e uno verticale su cui interviene la forza di gravità che tende a far cadere verso il suolo il proiettile Tarzan.

Tarzan parte da terra con un angolo ϑ rispetto alla linea orizzontale. La sua velocità  è costante e vale v.

La posizione di Tarzan in funzione del tempo t è descritta facilmente :

x(t) = v t cos ϑ                         ....(1)                      componente orizzontale (moto rettilineo uniforme)

y(t) = v t sen θ − ½ g  t²       ....(2)                      componente verticale (moto rettilineo uniformemente accelerato, con g accelerazione di gravità)

Il punto di caduta corrisponda al tempo t_P

La distanza L_P percorsa in orizzontale è data da:

L_P = v t_P cos ϑ

Mentre quella in verticale è, ovviamente, uguale a zero

v t_P sen θ −  ½ g  t_P² = 0

Ricavando t_P dalla prima, si ha:

t_P = L_P/(v cos θ)

Sostituendo nella seconda si ha:

Ma si sa che:

2 sen θ cos θ = sen 2θ

Per cui:

L_P = v² sen 2θ/g                  .... (3)

L raggiunge il massimo quando

dL/dθ = 0

(v²/g) 2 cos 2θ = 0

cos 2θ = 0

2θ = 90°

θ = 45°

L'angolo di alzo più favorevole è di 45° e la distanza percorsa è data dalla (3) in cui si pone θ = 45°.

L_P = v²/g                        .... (4)

Il tragitto più lungo si ottiene attraverso la (4)

La (1) permette di calcolare ogni distanza si voglia cambiando la direzione (θ) della velocità.

Tarzan potrebbe facilmente rappresentare la variazione di distanza percorsa al variare di θ (compreso tra o e 90°, dato che non vuole certo sparare sotto terra o sott'acqua e nemmeno indietro!). Basta che faccia il grafico della funzione (3)  che ora sa con certezza che ha un massimo a 45°, come mostrato in Fig. 2. La curva è ancora una parabola, ma non confondiamola con la traiettoria di Tarzan!

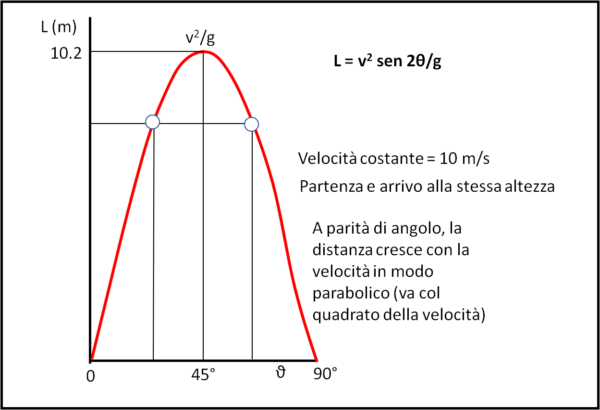
Tarzan nota  alcuni fatti fondamentali: la distanza massima va col quadrato della velocità. Esistono sempre due valori di θ che permettono di ottenere la stessa lunghezza della traiettoria L. In ogni caso, si ha sempre la massima distanza per θ = 45°.

A Tarzan non ci vuole molto a inserire la sua massima velocità da fermo (v = 10 m/s) e applicare la (4) al suo caso. Il risultato è sconfortante, dato che calcola giustamente una lunghezza massima del salto ottimale pari a 10.2 metri. Troppo poco rispetto agli F metri del fiume. Cadrebbe direttamente tra le fauci della belva affamata.

Tarzan deve escogitare qualcosa di meglio...

QUI la seconda puntata