Categorie: Fisica classica
Tags: altezze diverse angolo di gittata massima moto parabolico Tarzan e il coccodrillo
Scritto da: Vincenzo Zappalà
Commenti:0
Tarzan e il coccodrillo (seconda parte) **/***
Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.
Abbiamo lasciato Tarzan davanti al fiume con tanto di mostruoso coccodrillo al suo interno. L'idea di compiere un solo lunghissimo salto è stata accantonata: il fiume è troppo largo anche per Tarzan.
SECONDA PUNTATA
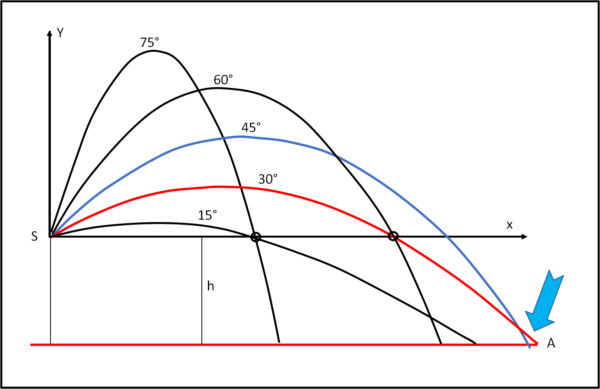
Tarzan si guarda attorno e vede che vi sono molte rocce su cui può facilmente arrampicarsi. Ve ne è una alta esattamente 10 m (chiama h la sua altezza) che cade a piombo sopra la sua attuale posizione S. Perché non salire su di lei e lanciarsi da quel punto? Gli sembra di ricordare che, partendo da un punto più alto del punto di arrivo, la traiettoria percorsa si allunghi, anche se l'angolo di alzo deve cambiare. Tarzan pensa di farcela a fare questo calcolo e si sposta sopra la roccia nella nuova posizione S, che ha altezza h sul livello del fiume (Fig. 3)
Tarzan sulla roccia
I calcoli eseguiti da Tarzan sono stati ritrovati sulla roccia sotto forma di graffiti che noi abbiamo cercato di riprodurre, con qualche libertà, nel testo che segue.
Tutte le possibili parabole partono adesso dal nuovo punto S che Tarzan considera nuovamente come origine. Il livello di arrivo si trova, ovviamente, a una distanza -h (è diretta verso il basso).
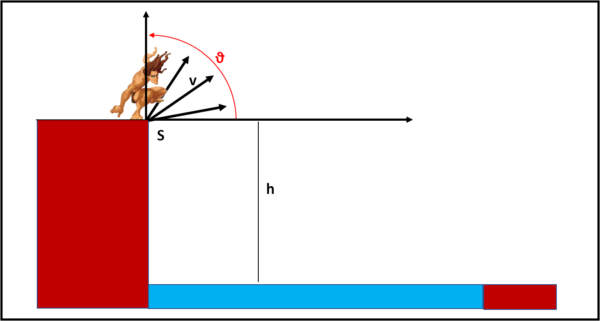
Prima di passare ai calcoli Tarzan anticipa il risultato finale in modo molto qualitativo, per capire a cosa sta andando incontro. noi usiamo la Fig. 4, che mette in bella copia i graffiti di Tarzan, dove le parabole sono state disegnate completamente ad occhio e vogliono solo rendere chiaro il punto critico della questione.
Tarzan vede subito che il massimo percorso, al variare di h, ossia differenza in verticale tra punto di partenza e punto di arrivo, modifica l'angolo di massima gittata: non è più 45°, ma un angolo sempre più piccolo al crescere di h.
Nella figura, è stato indicato con una freccia il caso in cui un lancio con un angolo di 30° riesce a superare la gittata dell'angolo di 45°. Tarzan passa, allora, a quantificare la situazione.
Riprende in mano le relazioni (1) e (2) che descrivono il moto parabolico.
x(t) = v t cos ϑ
y(t) = v t sen θ − ½ g t2
Quella orizzontale non cambia
LA= v tA cos θ .... (1)
Mentre quella in verticale non è più uguale a zero
v tA sen θ − ½ g tA2 = - h ....(2bis)
Se prima era un calcolo banale, dovrebbe restare banale anche adesso... c'è solo una "h" in più... ma mai fidarsi delle apparenze!
Si ricava tA dalla seconda:
Tarzan sceglie, ovviamente, il segno + davanti alla radice e inserendo nella (1) ottiene:
.... (3bis)
Beh... la situazione si è sicuramente più complicata rispetto alla (3) anche se, ponendo h = 0, torna a ottenere proprio lei:
(è sempre meglio fare delle prove come conferma dei calcoli...).
Tarzan passa al caso pratico e con h = 10 m e v = 10 m/s, la (3bis) gli mostra come non solo la distanza L sia cresciuta rispetto al caso precedente, ma anche come l'angolo di massima distanza sia diventato più piccolo, poco più di 30° (Fig. 5, dove è stata riportata anche la curva di Fig. 2.
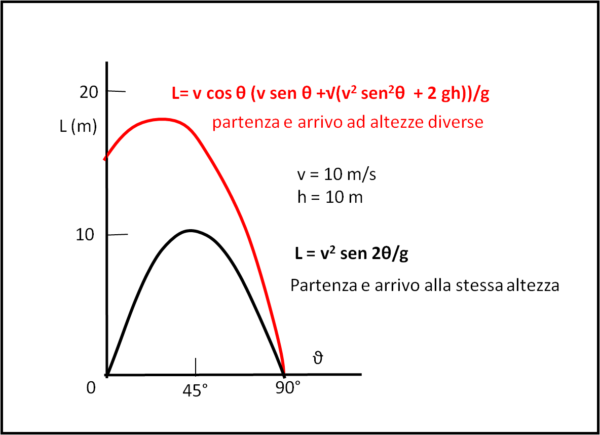
Non si può non notare che questa volta per un angolo di alzo di 0° si ha, comunque, un certo valore di L. Ciò è ovvio pensando che anche se Tarzan si lanciasse in orizzontale riuscirebbe a percorre un certa traiettoria prima di cadere in acqua. Per l'esattezza proprio mezza parabola... Il salto in perfetta verticale (θ = 90°) non porterebbe, invece, nessun miglioramento: sarebbe sempre una caduta seguendo la mela di Newton!
La curva è stata tracciata per punti. Tuttavia la (3bis) ha ancora una forma "accettabile" e Tarzan può tentare di farne la derivata e uguagliarla a zero per trovare quale valore ESATTO di θ gli regali il massimo della distanza in funzione del solo valore di h e di v (entrambi valori noti al nostro eroe). (non stupitevi se, malgrado tutte queste conoscenze, Tarzan fosse considerato "scarso" in fisica e matematica... la Scuola di Citoon è veramente la migliore e la più severa di tutta l'Africa!)
E' meglio separare LA nei suoi due "pezzi" (chiamiamola L per non portarci sempre dietro il pedice...):
e derivare rispetto a θ.
NOTA BENE: Chi vuole fare esercizio di derivate e trigonometria lo segua pure, gli altri possono saltare questa parte e andare direttamente alla formula (5))
Il denominatore non può mai essere zero per h diverso da zero
Ricordando che cos 2θ = cos2θ - sen2θ (formula di duplicazione)
sen2 θ (v2 cos(2θ) - 2hg)2 = v2 cos2(2θ)(v2 sen2θ + 2 gh)
sen2 θ (v4 cos2(2θ) + 4h2g2 - 4 v2hg cos(2θ))= v4 cos2(2θ)sen2θ + 2 ghv2 cos2(2θ)
v4 cos2(2θ)sen2 θ + 4h2g2 sen2 θ- 4 v2hg cos(2θ)sen2 θ= v4 cos2(2θ)sen2θ + 2 ghv2 cos2(2θ)
4h2g2 sen2 θ - 4 v2hg cos(2θ)sen2 θ= 2 ghv2 cos2(2θ)
Usa un trucchetto, ideato da Citoon...
sen2x + cos2 x = 1
sen2x +cos2x + sen2x - sen2x =1
cos2x -sen2x = 1 - 2sen2x
cos(2x) = 1 - 2 sen2x
4h2g2 sen2 θ - 4 v2hg (1 - 2 sen2 θ) sen2 θ = 2 ghv2 (1 - 2 sen2 θ)2
4h2g2 sen2 θ - 4 v2hgsen2 θ + 8v2hg sen4 θ = 2 ghv2 (1 + 4 sen4 θ - 4 sen2 θ)
4h2g2 sen2 θ - 4 v2hgsen2 θ + 8v2hg sen4 θ = 2 ghv2 + 8 v2ghsen4 θ - 8 ghv2 sen2 θ
4h2g2 sen2 θ - 4 hgv2sen2 θ = 2 ghv2 - 8 ghv2 sen2 θ
4hg sen2 θ +4v2sen2 θ = 2 v2
2 sen2 θ (hg + v2) = v2
sen2 θ = v2/2(hg + v2)
sen θ = v/√(2hg + v2) .... (5)
Nell'esempio fatto precedentemente ( h = 10 m, v = 10 m/s) otteniamo:
sen θ = 10/√2(98 + 100))
sen θ = 10/√396 = 0.502
θ = 30.2°
con cui, la (3bis) ci permette di calcolare la nuova gittata
LA = 17.5 m
Un bel guadagno, non c'è che dire, ma non basta ancora!
Beh...è stata dura, ma il risultato è sicuramente corretto.
Ovviamente, per h = 0, ossia partenza e arrivo alla stessa altezza, si ritrova:
θ = 45°
N.B. La parte che segue può essere saltata e andare direttamente alla puntata successivo, dato che Tarzan conosce perfettamente sia h che v, comunque è sempre uno studio interessante.
Tarzan, partendo dalla sponda più o meno alta sul pelo dell'acqua ha trovato qual è l'angolo che gli permette di effettuare il percorso più lungo, considerando h e v delle costanti. Tuttavia h e v possono variare. Ad esempio fissando l'altezza della sponda e facendo variare v. Bene l'angolo di massima gittata non è certamente fisso! Esso dipende dalla velocità... Se per h =0 l'angolo era sempre 45° per qualsiasi velocità, adesso non è più vero!
Basta fare il grafico della funzione
Imponendo un certo valore di h (ad esempio 10 m), vediamo in Fig. 6 che il sen θ aumenta sempre di più all'aumentare della velocità. Per velocità tendenti a infinito il valore del teta migliore tende a 45° (non sognatevi nemmeno di pensare a velocità relativistiche!!!).
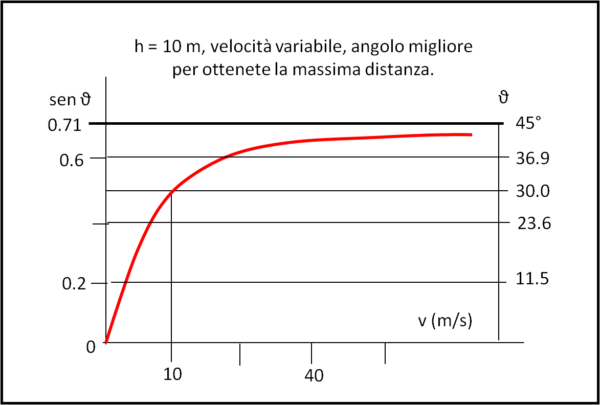
Se invece Tarzan ha una sua velocità fissa e ciò che varia è invece il baratro che si trova davanti, l'equazione diventa:
Poniamo v = 10 m/sec e otteniamo la curva che segue:
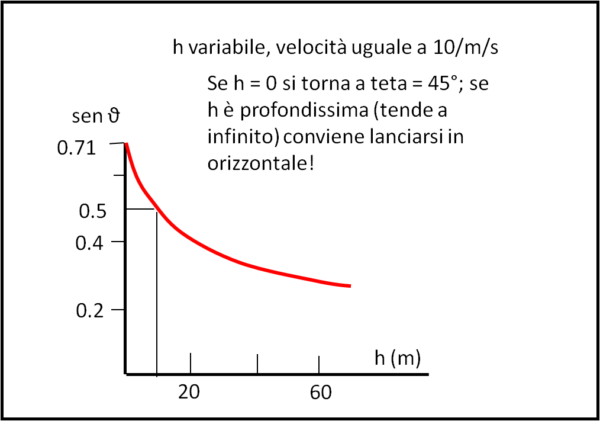
Ne segue nuovamente che se è al pelo dell'acqua gli conviene fare un salto a 45°, ma se, invece, il baratro è profondissimo è meglio che si lanci in orizzontale.
L'avventura di Tarzan prosegue... QUI la seconda parte.





