Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Nemmeno essere salito su una roccia a strapiombo sul fiume permette a Tarzan fare un salto sufficiente, mentre il coccodrillo si affila sempre più i denti. Cosa riuscirà a escogitare il nostro eroe?

Chi si fosse perso le prime due puntate, le può trovare QUI e QUI

 

TERZA PUNTATA

Tarzan si attacca alla liana

Niente da fare... non basta ancora. Il coccodrillo sembra sorridere quasi divertito, mentre l'urlo di aiuto continua a sentirsi attraverso la foresta. Purtroppo non ci sono rocce più alte a filo dell'acqua e partire da una roccia più alta, ma più lontana dalla sponda del fiume, è senz'altro una soluzione negativa.

Tarzan deve nuovamente pensare, anche se comincia ad avere mal di testa e il coccodrillo digrigna i denti in modo sicuramente plateale e voluto!

Il nostro eroe si siede sulla roccia e medita, infastidito dalla presenza di una liana che gli penzola proprio davanti al viso.... liana?! Ecco una nuova geniale soluzione! A questo punto comincia il ragionamento di Tarzan che ha sicuramente del buono, ma che mostra la sua mancanza di preparazione veramente all'altezza di Citoon. La liana  scende da un ramo e ha una lunghezza uguale a r (guarda caso proprio 10 m come l'altezza della roccia sul fiume).

Tarzan sale su una roccia in modo da poter tendere la liana in orizzontale, ossia a 90° esatti rispetto alla verticale (andare più in alto non servirebbe a niente perché la corda non potrebbe restare tesa...). La situazione è rappresentata schematicamente in Fig. 8.

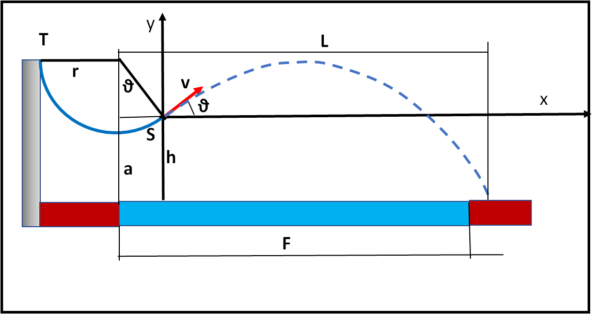
Cosa guadagnerebbe Tarzan sfruttando la liana? Sicuramente molto. Giustamente lui pensa che, innanzitutto, arriverebbe nel punto S della roccia a picco sul fiume con una velocità  maggiore dei suoi 10 m/s raggiungibili da fermo. Ma, cosa ancora più importante, potrebbe restare attaccato alla liana e lasciarsi andare  in un punto più vicino alla sponda opposta e anche a un'altezza maggiore. La Fig. ... illustra questo ragionamento che sembra ineccepibile. In poche parole, è come se Tarzan si trovasse su una roccia più alta e più vicina alla sponda opposta e staccandosi iniziasse il suo moto parabolico che già conosce. Andrebbe tutto bene, ma... il problema è calcolare la velocità...

Prima, infatti, la velocità era conosciuta, mentre adesso dipende dal movimento di Tarzan attaccato alla liana. Ma no, Tarzan si ricorda dei giochi fatti con Cita scivolando da una collinetta perfettamente liscia e risalendo su quella opposta. Tutto si basava sulla conservazione dell'energia. Quando era in alto e fermo, l'energia era solo potenziale e valeva:

E = gmh₁     dove h₁ era l'altezza della collinetta.

Lasciandosi andare diminuiva la sua energia potenziale, ma aumentava quella cinetica. Nel punto più basso (in questo caso con la liana in verticale) l'energia era in parte ancora potenziale e in parte cinetica, secondo la formula:

E = gmh₂ + 1/2 mv₂

Ma h₁ nel caso di Tarzan era proprio r + h = 10 + 10 = 20 m, mentre h₂ era solo h = 10 m.

Le due relazioni, per la conservazione dell'energia, devono essere uguali, ossia:

gmh₁ = gmh₂ + 1/2 mv²

gm(h + r) = gmh + 1/2 mv²

gmr = 1/2 mv²

v² = 2gr

v = √(2gr)

Nel caso di Tarzan:

v = √(2· 9.8 ·10) = 14 m/s

Eureka! In questo modo  arriva allo stesso punto S di prima con una velocità maggiore. Sì, ha ragione, ma la velocità comincia poi a diminuire mentre la liana lo riporta verso l'alto. Quando è massima è diretta orizzontalmente, ma l'angolo migliore per lasciarsi andare è sicuramente un altro. Infatti, Tarzan non sta assolutamente compiendo un moto circolare uniforme attorno al punto di origine della liana. Lui risale diminuendo sempre più la velocità che torna a zero quando la liana raggiunge nuovamente la posizione orizzontale

In parole ancora più semplici, la velocità di Tarzan non è più un parametro separato e indipendente da θ, ma è strettamente legata all'angolo.

A questo punto nessuno conosce esattamente cosa abbia fatto Tarzan. Forse ha tentato di calcolare la nuova parabola con  velocità costante o forse no... sicuramente è entrato in confusione. Il problema era troppo grosso per lui.

Voci di foresta dicono che abbia, comunque, pensato e calcolato a lungo, troppo a lungo. Infatti, nel frattempo, il gorilla dei monti Virunga se l'era cavata da solo (facendo un gesto verso Tarzan inequivocabile, ma non riproducibile per problemi di censura), il coccodrillo si era dimostrato vegetariano, dirigendosi  verso un bel mucchio di fiori di loto, suo cibo preferito, il maestro Citoon aveva scosso a lungo la testa pensando a quanto fossero serviti poco i suoi insegnamenti, pensando tra sé e sé: "Puoi allevarli come vuoi, ma se sono uomini rimangono uomini!".

Tarzan, in effetti, non aveva cavato un ragno dal buco e, vista la situazione, s'era fatto una bella nuotata, mentre il coccodrillo si stava ancora leccando i baffi (ma i coccodrilli hanno i baffi?). Cita, tornata anticipatamente, lo aveva poi portato, amorevolmente, nella sua casa sull'albero. Tutto è bene quel che finisce bene.

Tarzan diventa un pendolo

Noi però non possiamo lasciare  la faccenda incompiuta e sappiamo bene che tipo di moto fa Tarzan mentre è attaccato alla liana: un moto armonico, ossia quello del pendolo. Un moto interessantissimo che ha diverse caratteristiche eccezionali, già conosciute, ad esempio, da Galileo che così racconta:

" ... volendo che ’l tempo d’una vibrazione d’un pendolo sia doppio del
tempo d’una vibrazione d’un altro, bisogna che la lunghezza della corda di quello
sia quadrupla della lunghezza della corda di questo; ed allora, nel tempo d’una
vibrazione di quello, un altro ne farà tre, quando la corda di quello sarà nove volte
più lunga dell’altra: dal che ne séguita che le lunghezze delle corde hanno fra di loro
la proporzione che hanno i quadrati de’ numeri delle vibrazioni che si fanno nel
medesimo tempo..."

Questa peculiarità si vede molto bene in questo filmato estremamente affascinante

Noi sappiamo che il periodo del pendolo può essere calcolato facilmente solo per oscillazioni molto piccole. Fortunatamente nel caso di Tarzan il periodo conta ben poco e quello che interessa è soltanto il legame tra velocità e angolo θ. Inoltre, mentre prima l'altezza h era un dato del problema, adesso è una variabile anch'essa, essendo l'altezza del punto di distacco di Tarzan dalla liana.

Chiamiamo perciò a la distanza tra l'estremità bassa della liana in verticale e il terreno (o fiume).  In parole più matematiche si ha che:

h = a + r (1 - cosθ)

come si vede bene in Fig. 8.

Nel caso di Tarzan a era proprio uguale a r, ma noi possiamo prenderli anche diversi tra loro per maggiore generalità poi potremo calcolare il valore della distanza percorsa proprio per il caso tarzaniano (a = r)

Consideriamo, finalmente, la nostra liana+Tarzan un vero pendolo e applichiamogli il principio di conservazione dell'energia, che abbiamo già usato precedentemente. Facciamolo pure partire con un angolo uguale a 90° (α = 90°).

In un punto qualsiasi dell'oscillazione, Tarzan è soggetto sia all'energia potenziale che a quella cinetica, ma la loro somma deve essere uguale a quella di partenza (solo potenziale). Ossia:

mg(a + r) = mgh + 1/2 mv²

ma

h = a + r(1 - cos θ)

mg(a + r) = mg(a +r(1-cos θ)) + 1/2 mv²

mga + mgr = mga + mgr  - mgrcosθ +1/2mv²

1/2 mv² = mgrcosθ

v² = 2 g r cos θ                       

A questo punto basta andare a sostituire nella (3b) la nuova velocità? Non basta ... dobbiamo anche aggiungere il tratto orizzontale, che vale semplicemente r sen θ, percorso attaccato alla liana, dalla sua posizione verticale fino al raggiungimento dell'angolo θ di distacco.

La (3bis) diventa:

              

eliminiamo la apparente dipendenza  da g

       

moltiplicando e dividendo per √(r cos θ) il terzo membro

                              

                                               

a + r è veramente un dato legato alle condizioni iniziali (è proprio l'altezza della cima della liana rispetto  livello del terreno)  e possiamo chiamarlo T

                   .... (5)

Basterebbe derivare questa funzione, azzerarla e avremmo come risultato l'angolo a cui Tarzan deve staccarsi per compiere il tragitto massimo tra il momento della liana in verticale e il momento in cui tocca terra.

No, un qualcosa che Tarzan non avrebbe potuto fare né con i graffiti né sulla sabbia.

Noi però possiamo usare metodi più moderni... li scopriremo nella prossima puntata!