Questo articolo è stato inserito nelle sezioni d'archivio "Matematica e Geometria" e "Dinamica e Meccanica"

Tensegrity

L'immagine seguente raffigura due oggetti filiformi identici, ottenuti , per esempio, con filo di rame di diametro sufficiente a conferigli una adeguata rigidezza. Anche il più volgare fil di ferro va benissimo. Il filo è ripiegato a formare quattro dei sei spigoli di un tetraedro regolare, come in figura. Uno dei due oggetti è appoggiato con la sua base a triangolo equilatero su un tavolo (non rappresentato in figura). Il secondo oggetto è capovolto e posto ad una certa altezza dal tavolo. Guardando l'immagine si è portati a pensare che il secondo oggetto, lasciato libero da ogni vincolo, non potrà che cadere sul primo, sotto l'azione della forza di gravità.

In realtà, il sistema rimane perfettamente in equilibrio, con l'oggetto superiore che resta esattamente dove lo vediamo nell'immagine. Questo accade per la presenza di quei fili appena visibili in figura, uno centrale, più corto, che collega il vertice in alto dell'oggetto appoggiato sul tavolo con il vertice in basso dell'oggetto capovolto, e gli altri tre, più lunghi, che collegano i vertici della base triangolare dell'oggetto in basso con i punti medi dei lati del triangolo dell'oggetto capovolto.

In questo articolo analizzerò un po' più da vicino questo particolare tipo di strutture, basate sul principio della "tensegrity", ossia su un sistema di componenti tra loro isolati e tenuti insieme in equilibrio all'interno di una rete di elementi tesi. Il termine anglosassone "tensegrity", infatti, proviene dall'unione delle due parole inglesi "tension" (tensione) e "integrity" (integrità).

Analisi cinematica

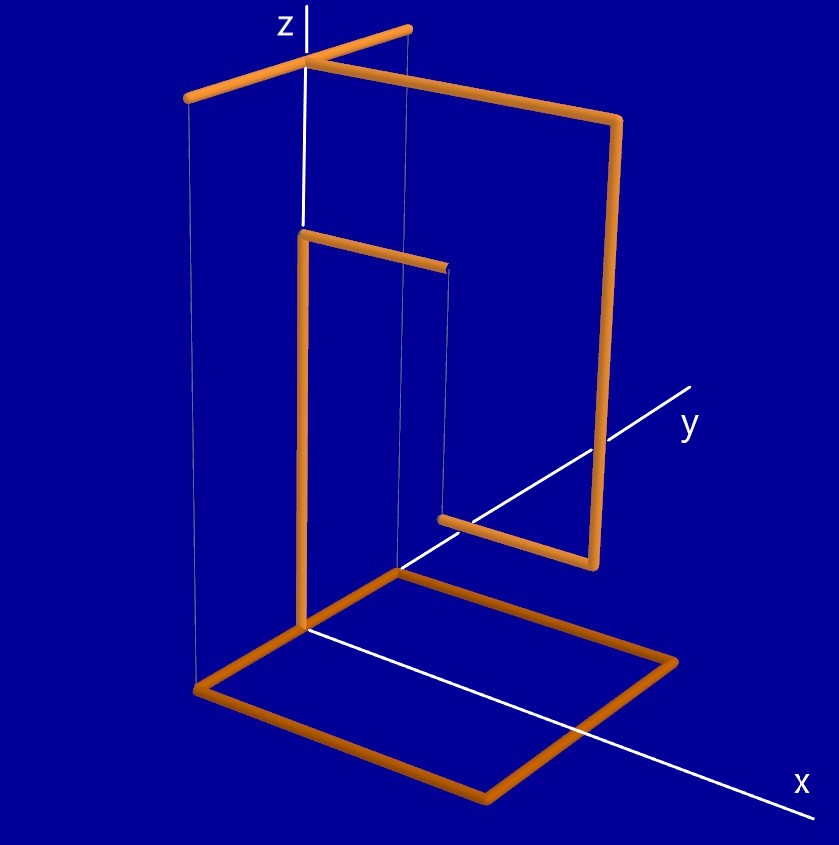
Per agevolare la trattazione analitica dell'equilibrio, prenderò in considerazione un sistema tridimensionale, come quello dell'immagine precedente, ma che può facilmente essere riportato nel piano. Questa circostanza, come vedremo, semplifica notevolmente il calcolo dell'equilibrio. Tale sistema è concettualmente identico a quello precedente. Abbiamo, anche in questo caso, un oggetto appogiato su un tavolo e uno sospeso  al disopra del primo, il tutto in perfetto equilibrio. In questo caso, per semplicità, ipotizziamo che l'oggetto inferiore sia proprio fissato, non solo appoggiato, ad un tavolo. Esso , cioè, non può muoversi in alcun modo.  Il sistema oggetto della trattazione analitica è quello visibile nella seguente immagine:

Anche questo può essere agevolmente autocostruito.

Le ipotesi di partenza sono:

• che il sistema sia costituito da due corpi rigidi, indeformabili. Il corpo rigido è in fisica un sistema materiale caratterizzato dal fatto che, presa una qualsiasi coppia di suoi punti, la loro distanza resta costante. Il corpo rigido inferiore è saldamente fissato ad un tavolo.
• i fili siano inestensibili e di massa trascurabile. Nella realtà, qualsiasi materiale utilizzato per la realizzazione dei fili avrà una suo allungamento se in trazione. Nella trattazione ipotizzerò che questo allungamento sia trascurabile.
• gli spostamenti impressi dall'esterno all'oggetto superiore, rispetto alla sua iniziale posizione di equilibrio, siano piccoli , comunque tali che i fili restino in tensione.

Fissiamo un sistema di assi cartesiani nello spazio come nells eguente figura:

Un qualsiasi corpo rigido, nello spazio, libero da qualsiasi vincolo,  ha sei gradi di libertà. Cosa significa questa affermazione ? Faccio riferimento al sistema preso in considerazione. L'oggetto superiore, se non fosse vincolato dai tre fili, potrebbe traslare nella direzione dei tre assi cartesiani x, y e z, e potrebbe ruotare attorno alla loro direzione. Potendosi muovere in 6 differenti modi, quindi, si dice che esso ha 6 gradi di libertà.

Applichiamo ora i fili visibili in figura. Iniziamo con il filo centrale.  Il filo centrale gioca un ruolo importante perché tramite esso l'oggetto superiore viene sospeso a quello inferiore. Esso , quindi, impedisce all'oggetto superiore di traslare lungo l'asse z verso il basso. Non impedisce , però, la traslazione lungo l'asse z verso l'alto, perché il filo, in quanto tale, è inefficace se cerchiamo di accorciarlo. Semplicemente si piega. Tanto meno il filo centrale impedisce all'oggetto superiore di traslare lungo l'asse x o lungo l'asse y. Infine, esso non impedisce la rotazione dell'oggetto superiore attorno alla direzione di alcuno dei 3 assi cartesiani.

Applichiamo ora i due fili laterali. Essi impediscono all'oggetto superiore di spostarsi verso l'alto lungo la direzione dell'asse z per traslazione. Infatti, se si cerca di sollevare l'oggetto superiore parallelamente alla direzione dell'asse z, essi vanno in trazione e, essendo per ipotesi inestensibili, trattengono il ramo dell'oggetto a cui sono collegati. In pratica, perché l'oggetto si sollevi, dovrà ruotare attorno al ramo a cui sono ancorati i due fili laterali, come si vede nella seguente animazione con il modello visto di fianco.

L'oggetto superiore, invece, puo' traslare lungo la direzione dell'asse x o dell'asse y. Essendo, però, i fili inestensibili per ipotesi, il reale movimento sarà una rototraslazione, ossia una traslazione lungo la direzione dell'asse x  accompagnata da una rotazione attorno alla direzione dell'asse y. La seguente animazione di traslazione pura lungo l'asse x dimostra graficamente questa circostanza. In essa è visibile la lunghezza dei fili aggiornata in tempo reale man mano che la traslazione progredisce. Si nota che una traslazione pura lungo x imporrebbe un allungamento dei fili e ciò non è possibile avendo ipotizzato che i fili siano inestensibili.

Naturalmente, traslando in direzione dell'asse x, la tensione nei fili non risulterà più perpendicolare al piano xy, ma inclinata. In particolare, spostando l'oggetto verso destra, la tensione nel filo corto centrale avrà una componente lungo l'asse x diretta verso sinistra. Analogamente, la tensione nei due fili lunghi laterali avrà una componente lungo l'asse x diretta verso sinistra. In pratica, i fili si opporranno alla traslazione lungo l'asse x , tendendo a riportare l'oggetto nella sua iniziale configurazione di equilibrio.

Stesso discorso se consideriamo una traslazione lungo la direzione dell'asse y. Anche in questo caso avremmo in realtà una rototraslazione con la tendenza dei fili a riportare l'oggetto nella sua iniziale configurazione di equilibrio.

Passiamo, ora, alla rotazione attorno agli assi.

I tre fili, in teoria, non impediscono la rotazione dell'oggetto superiore attorno all'asse z. Tuttavia, si nota agevolmente che , anche in questo caso, il moto di rotazione imporrebbe un allungamento dei tre fili, come si evince dalla seguente animazione. Notare l'aumento della lunghezza dei fili al progredire della rotazione attorno all'asse z.

Il fatto che i fili siano inestensibili comporta che , in realtà, se imprimiamo all'oggetto superiore una rotazione attorno all'asse z di un certo angolo e poi lo lasciamo libero, esso torna alla configurazione iniziale di equilibrio dopo qualche oscillazione. Questo perché, per effetto della rotazione impressa, le tensioni nei due fili laterali lunghi non sono più perpendicolari al piano xy ma si inclinano, inducendo una coppia "di richiamo" che tende  a riportare l'oggetto alla situazione iniziale.

Consideriamo, ora, la rotazione attorno alla direzione dell'asse x. Essendo due i fili laterali lunghi e messi da parte opposta rispetto all'asse x, è abbastanza intuitivo che essi impediscano la rotazione dell'oggetto superiore attorno alla direzione dell'asse x. Infatti, se cerchiamo di far ruotare l'oggetto attorno alla direzione dell'asse x in senso orario, va in trazione il filo di sinistra. Se cerchiamo di farlo ruotare attorno alla direzione dell'asse x in senso antiorario, va in trazione il filo di destra. In entrambi i casi, la rotazione sarebbe ostacolata dal filo in trazione, inestensibile per ipotesi.

Vediamo, infine, la rotazione dell'oggetto superiore attorno alla direzione dell'asse y. Nella prima animazione si è già visto che tale rotazione è possibile nel verso che tende e sollevare l'oggetto. Non è, invece, possibile farlo ruotare nel verso opposto, se i fili restano in tensione. Osserviamo la seguente animazione.

Si noti che, comunque si posti l'oggetto superiore, verso destra o verso sinistra rispetto all'equilibrio iniziale, la rotazione dell'oggetto è sempre in verso antiorario. Questo finché i fili restano in tensione. Quindi, la rotazione attorno alla direzione dell'asse y è possibile ma solo se impressa dall'esterno e, entro certi limiti (fili in tensione), l'oggetto tende a riportarsi alla posizione di equilibrio iniziale.

Quale è , dunque, l'effetto combinato della presenza dei tre fili ? Il filo centrale sostiene l'oggetto superiore, impedendo che cada. I due fili laterali, invece, impediscono che questo ribalti ruotando attorno al punto di sospensione. Tutti e tre, infine, contribuiscono a stabilizzare l'equilibrio, tendendo a riportare l'oggetto superiore nella sua posizione iniziale, qualora lo si sposti, entro certi limiti, da essa.

Analisi Statica

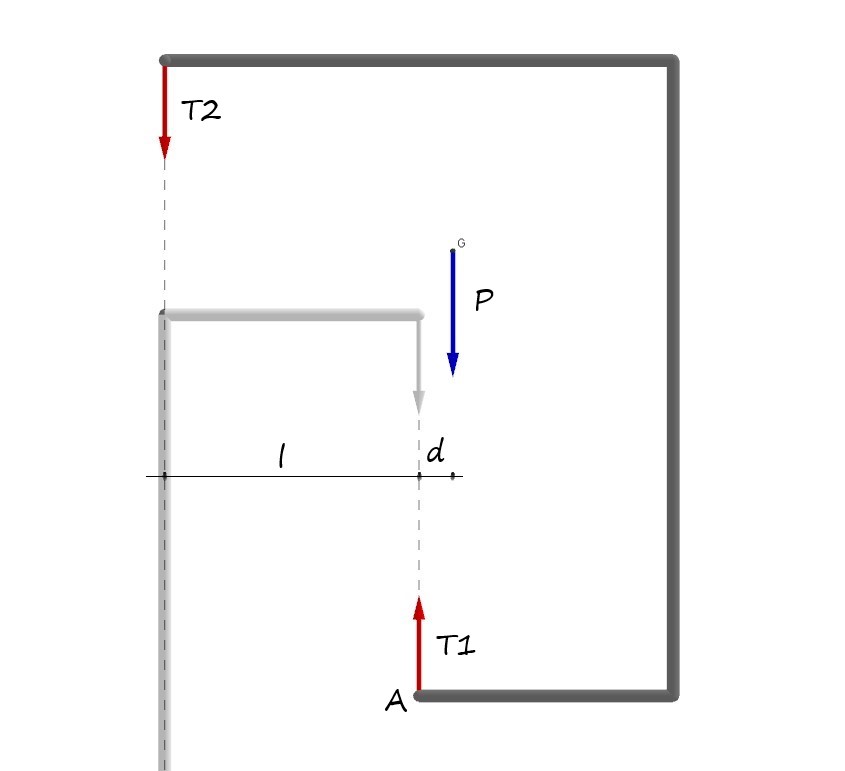
Immaginiamo, allora, di "appiattire" il sistema nel piano coordinato xz (perpendicolare all'asse y). Quello che vedremmo è rappresentato nella seguente immagine.

Nel piano xz considerato, l'oggetto superiore , se libero da ogni vincolo, potrebbe solo traslare lungo la direzione parallela all'asse x o quella parallela all'asse z e ruotare attorno alla direzione parallela all'asse y (perpendicolare al piano xz). Considero la situazione in cui l'oggetto superiore è in equilibrio come in figura. Le tensioni nei fili, quindi,  avranno componente non nulla solo nella direzione dell'asse z, perché i fili , in tale configurazione di equilibrio, sono perpendicolari all'asse x. Chiamo T1 la tensione nel filo corto centrale e T2 la tensione nel filo lungo  a sinistra. Rammentiamo che abbiamo appiattito nel piano xz il sistema tridimensionale nel quale i fili lunghi erano due, per cui , in realtà, il simbolo T2 nel piano xz rappresenta la somma delle tensioni nei due fili lunghi. Chiamo con P il peso dell'oggetto superiore, naturalmente applicato nel suo centro di massa G.

Pensando, ora, di separare l'oggetto superiore dai tre fili che lo tengono in equilibrio, al posto di questi ultimi dovrò metterci le rispettive tensioni, cambiate di verso, che agiscono sull'oggetto. Pertanto, l'azione esercitata dal filo corto centrale sull'oggetto è pari a T1 e rivolta verso l'alto. Analogamente, l'azione esercitata dai due fili lunghi sull'oggetto è pari a T2 e rivolta verso il basso.

Per l'equilibrio alla traslazione lungo la direzione dell'asse z, dunque, posso scrivere:

                  (1)

T1 è con il segno + perché rivolto verso l'alto, come l'asse z. T2 e P sono con il segno - perché rivolti verso il basso, quindi opposti al verso dell'asse z.

Fisso ora come positivo il verso di rotazione orario.

Per l'equilibrio alla rotazione attorno ad un qualsiasi punto del piano xz, per esempio attorno al punto A, devo equilibrare i momenti delle forze rispetto ad A. Ricorderemo che, nel piano, il modulo del momento di una forza rispetto ad un punto è dato dal prodotto dell'intensità della forza per il braccio, ossia per la distanza (misurata perpendicolarmente) del punto dalla retta di azione della forza. Nel nostro caso avremo, rispetto al punto A :

     (2)

Il prodotto Pd ha il segno + perchè il peso dell'oggetto superiore tende a farlo ruotare in verso orario, quindi concorde al verso positivo prefissato. Il prodotto T2l ha segno - perché la tensione dei due fili lunghi tende a far ruotare l'oggetto superiore in verso antirorario, dunque discorde al verso positivo prefissato.

Mettendo a sistema la (1) e la (2) si ottiene subito:

                    (3)

 

                     (4)

Ora, mentre l è un dato geometrico immediatamente visibile del problema, d , invece, è la distanza , misurata lungo l'asse x, tra il centro di massa dell'oggetto superiore e il punto A. Devo, quindi, calcolare preliminarmente le coordinate del centro di massa G dell'oggetto superiore.

Per la simmetria del sistema rispetto al piano coordinato xz, possiamo già dire che il centro di massa giace su tale piano. La sua coordinata , quindi, è pari a zero. Calcoliamo le altre due coordinate e . Esplicitiamo, prima, la geometria e la distribuzione di massa dell'oggetto superiore. Esso è composto da:

• (a) un tratto orizzontale perpendicolare al piano xz, di lunghezza pari a 2 metri;
• (b) un tratto orizzontale parallelo all'asse x, di lunghezza pari a 2 metri;
• (c) un tratto verticale , di lunghezza pari a 2,5 metri;
• (d) un tratto orizzontale parallelo all'asse x , di lunghezza pari a 1 metro.

La densità lineare dell'oggetto sia costante nei vari tratti e sia, per esempio, pari a 1 kg/m . Cioè, un tratto lungo 1 metro abbia una massa pari a 1 kg. Per quanto sopra:

• (a) la massa ma del tratto è pari a 2 kg e il suo centro di massa si trova in Ma , punto medio del tratto (a);
• (b) la massa mb  del tratto è pari a 2 kg e il suo centro di massa si trova in Mb, punto medio del tratto (b);
• (c) la massa mc del tratto è pari a 2,5 kg e il suo centro di massa in Mc, punto metio del tratto (c);
• (d) la massa md del tratto è pari a 1 kg e il suo centro di massa si trova in Md, punto medio del tratto (d).

Conoscendo le coordinate dei punti Ma, Mb, Mc, Md, date dalla geometria nota dell'oggetto, si calcolano le coordinate del centro di massa G dell'intero oggetto mediante le formule:

Sostituendo i valori numerici alla fine si ottiene:

xG=1,13 m

zG=2,75 m

A questo, punto, posso determinarmi d :

Quindi, dalle (3) e (4), essendo

ottengo:

Come detto prima, T2 in realtà è la somma delle tensioni nei due fili lunghi laterali che, per la simmetria del sistema, sono tra loro uguali. Quindi, la tensione in ciascuno dei due fili lunghi laterali sarà pari alla metà di T2.

Notare la notevole differenza tra la tensione nei due fili lunghi e quella nel filo corto centrale.

Realtà aumentata

Facciamo ora un... incontro virtuale in realtà aumentata con l'oggetto del nostro studio. Quello che segue è un video realizzato con uno smartphone su cui è installata l'app Geogebra 3D. L'oggetto ripreso nel video in realtà non è fisicamente presente, è solo un modello virtuale immerso nell'ambiente circostante, nel quale l'osservatore può spostarsi liberamente. Per questo nel video si vede il modello ma non la sua ombra. In realtà, infatti, non esiste. Il contesto in cui il video è stato registrato è un cantiere edile. Naturalmente, ero da solo, per evitare che eventuali osservatori si chiedessero cosa diavolo stessi riprendendo (loro avrebbero visto solo la platea in calcestruzzo recentemente realizzata   )

 

Approfondimento cinematico 

Ora osserviamo la seguente animazione. Essa riprende l'oscillazione del sistema attorno alla posizione iniziale di equilibrio sopra analizzata. L'ampiezza delle oscillazioni è stata amplificata per maggiore chiarezza.

Una constatazione  che viene quasi spontanea, osservandola, è che tra i due angoli    e  rappresentati in figura ci deve essere una relazione attraverso la quale, stabilito il valore di uno è univocamente determinato il valore dell'altro. Ci proponiamo di determinare questa relazione tra i due suddetti angoli.

Facciamo riferimento alla seguente figura:

Ho indicato con R la lunghezza dei fili lunghi, con r la lunghezza del filo corto. Ho , inoltre, rappresentato gli assi x (orizzontale) e z (verticale). Finchè i fili sono entrambi in tensione, il punto A e il punto B si muovono, rispettivamente, su archi di circonferenza, in particolare  circonferenza cA il primo e  circonferenza cB il secondo. Posso scrivere le coordinate del punto A in funzione dell'angolo gamma , a meno del segno, come segue

Al variare dell'angolo gamma , il punto A percorre, appunto, un arco della circonferenza ca di raggio R.

Analogamente, per il punto B:

Al variare dell'angolo delta , il punto B percorre un arco della circonferenza cb di raggio r.

Ora, poiché l'oggetto superiore è un corpo rigido, la distanza tra due suoi punti qualsiasi deve restare costante. In particolare, se prendiamo i punti A e B, la loro distanza, al variare degli angoli gamma e delta, deve restare pari a quella iniziale (dato geometrico). Traduciamo questa proprietà in una equazione. La distanza tra i due punti A e B, in geometria analitica, è data da:

                                     (5)

La distanza AB iniziale , che chiamo k, è data da:

                                                 (6)

dove Ao e Bo sono le posizioni iniziali dei punti A e B.

Utilizzo nella (5) le espressioni trovate prima per xA, zA, xB, zB e ricordo che ho posto AB=k:

Nella suddetta equazione, le variabili sono gli angoli gamma e delta. Tutti gli altri parametri sono dati del problema.

Svolgendo i calcoli , alla fine ottengo la seguente equazione che lega tra loro gli angoli delta e gamma   (7):

Purtroppo, non è affatto agevole esplicitare la suddetta relazione rispetto a una delle variabili (per esempio l'angolo gamma), ottenere, cioè, una equazione del tipo

Possiamo, tuttavia, trarre qualche informazione anche dalla suddetta relazione implicita tra le due variabili.

Per esempio, per angoli molto piccoli (ricordiamo che le oscillazioni nel piano xz sono piccole), posso approssimare il seno di un angolo all'angolo medesimo e il coseno dell'angolo a 1. In questo caso, la (7) diventa:

cioè:

                               (8)

Ora, se nella suddetta relazione, al posto di k vado a sostituire la sua espressione data dalla (6) e considero che , per la geometria del sistema, risulta:

allora il secondo membro della (8) risulta pari a zero. Pertanto, la (8) diventa:

da cui, esplicitando rispetto all'angolo delta, ottengo:

In definitiva, per piccole oscillazione nel piano xz, l'angolo delta è R/r   volte l'angolo gamma. Nel caso specifico R/r = 3,5/1,5 = 2,33.

Nel caso generale, comunque per valori degli angoli tali che i fili restino in tensione, si potrebbe considerare la (7) come funzione di due variabili (i due angoli delta e gamma). Il suo grafico , nello spazio cartesiano delta,gamma,z sarebbe il seguente, ricavato con Geogebra:

L'intersezione tra la suddetta superficie e il  piano coordinato z=0  è il luogo dei punti per i quali vale la (7) ,  visibile nel seguente grafico:

 

Di tale curva interessa solo un tratto intorno all'origine, di ampiezza tale che , comunque, i fili restino in tensione.

Realizzazione pratica

Bene, dopo la teoria, è bello mettere in pratica. Quello che segue è il video realizzato con il modellino reale.

Per realizzarlo ho utilizzato del comune fil di ferro, di diametro sufficiente ad ottenere una certa rigidezza senza renderlo troppo difficile da piegare per fargli assumere la forma richiesta. Per i fili ho utilizzato una corda sottile gentilmente messa a disposizione da mia moglie. Naturalmente, il modello da me realizzato è composto da due oggetti non esattamente assimilabili a corpi rigidi (indeformabili). Si nota nel video, infatti, come l'asta verticale dell'oggetto inferiore tenda a flettersi quando provo a fare una leggera pressione sull'oggetto superiore. Sicuramente, un risultato più aderente al modello teorico si otterrebbe realizzando un modello più rigido. Da notare che i fili lunghi sono visivamente meno tesi di quello corto centrale, in accordo con quanto ricavato dalla teoria. Il modello, come più volte precisato nell'articolo, funziona se i tre fili restano in tensione. Non appena uno dei fili lunghi laterali si affloscia, magari perchè il baricentro sbanda troppo fuori dal piano xz, l'oggetto superiore ribalta rovinosamente sul tavolo.

Bene, se avete avuto la pazienza di leggere fino a qui e ora vi è venuta voglia di fare anche voi un modellino simile, magari con materiali diversi, sarebbe bello se ne pubblicaste qualche foto nei commenti.