Categorie: Matematica
Tags: area spazzata capretta Carnot Erone geometria quiz soluzione tosaerba trigonometria
Scritto da: Vincenzo Zappalà
Commenti:0
Soluzione del quiz sulla capretta tosaerba ***
Ecco due soluzioni per la nostra capretta tosaerba molto efficiente, con la seconda trovata dal nostro instancabile Fabrizio, che ringrazio di cuore.
1) d ≤ b < a
In questo caso la corda è molto corta e la capretta non può fare altro che brucare all'interno del cerchio verde di Fig. 1.
Per essere precisi, la capretta "spazza" un'area STOT uguale a 3/4 di quella del cerchio verde:
STOT = 3/4 π d2
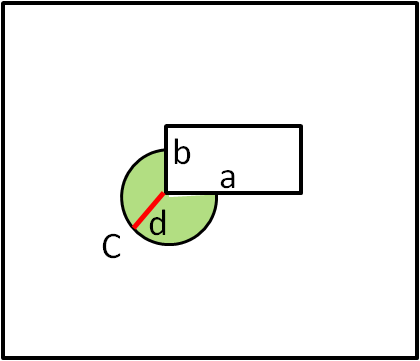
2) b < d ≤ a
In questo caso la corda è maggiore del lato più corto (b) della casa, ma è minore (o uguale) al lato più lungo (a)
La situazione è rappresentata in Fig. 2

La capretta spazza tranquillamente i 3/4 del cerchio di raggio d, ma riesce a fare qualcosa di più, dato che quando la corda si tende lungo il lato corto della casa, la capretta può ancora brucare 1/4 del cerchio di raggio d - b.
STOT = 3/4 π d2 + 1/4 π (d - b)2
3) a < d ≤ (a + b)
in questo caso d è maggiore sia di b che di a (ma non della loro somma). La situazione è rappresentata in Fig. 3.

La capretta spazza, come sempre, i 3/4 del cerchio verde di raggio uguale a d. E' però in grado di eliminare l'erba anche nelle due zone azzurra e rossa che sono uguali a 1/4 dei cerchi di raggio d - b e d - a, rispettivamente.
STOT = 3/4 π d2 + 1/4 π (d - b)2 + 1/4 π (d - a)2
E' interessante riportare anche il caso limite in cui d = a + b, come fatto in Fig. 4.

La capretta spazza i soliti 3/4 del cerchio di raggio d, ma, inoltre, anche 1/4 dei cerchi di raggio a e b, dato che d - a = b e d - b = a. Risulta, quindi:
STOT = 3/4 π (a + b)2 + 1/4 π a2 + 1/4 π b2
STOT = 3/4 π a2 + 3/4 π b2 + 3/2 π ab + 1/4 π a2 + 1/4 π b2
STOT = π a2 + π b2 + 3/2 π ab
4) d > (a + b)
L'ultimo caso è quello decisamente più complicato (dove si è impegnato Fabrizio). Vediamo, in Fig. 5, la situazione.

La capretta non ha alcun problema a brucare tutta l'erba del cerchio verde. Per essere precisi i 3/4 del cerchio verde. Poi, la corda viene bloccata dagli spigoli della casa (disegnata in bianco) e la nostra tosaerba è costretta a descrivere i cerchi di raggio d - b (azzurro) e d - a (rosso). In realtà, però, brucando solo 1/4 di questi cerchi, è costretta a brucare DUE volte la stessa area e quest'ultima non può essere contata due volte, ma solo UNA. La parte comune è quella dipinta in viola.
La soluzione apparentemente più semplice sembrerebbe quella di sommare il quarto di cerchio rosso al quarto di cerchio azzurro e, ovviamente, i tre quarti del cerchio verde e, poi, togliere l'area viola. Quest'ultima non è però cosa semplice da calcolare. Ci sono vari modi per riuscire nell' intento. Il più "elegante" matematicamente sarebbe quello di usare gli integrali, dato che le curve che delimitano la parte viola sono ben conosciute così come i punti di inizio e fine. La capretta, però, non conosce gli integrali, ma solo la trigonometria e la geometria, per cui dobbiamo usare un approccio diverso. Scegliamo quello della somma invece che quello della sottrazione. Mi spiego meglio...
A parte i 3/4 del cerchio verde, vediamo come si può rappresentare la parte rimanente. Facciamo uno "zoom" di quest'ultima, aggiungendo alcune lettere e qualche segmento, come descritto in Fig. 6, a sinistra.

Sfruttando i segmenti AI e BI (I è il punto di intersezione delle circonferenze azzurra e rossa), possiamo trasformare l'area desiderata in modo diverso come mostrato nella Fig. 6, a destra.
A questo punto, risulta evidente che la parte ancora da determinare è composta da tre zone: il settore circolare BQI, il settore circolare API, più il quadrilatero BIAR. Non ci resta che determinare le aree di queste tre figure e il gioco è fatto! Oltretutto, è un bel ripasso della formula di Erone e del teorema di Carnot (poco prima della Fig. 17)...
Cominciamo con il quadrilatero...
La sua area è uguale a quella del triangolo BAI meno l'area del triangolo rettangolo AOB.
Iniziamo a calcolare l'area del triangolo BAI. Di questo conosciamo la lunghezza dei tre lati, dato che BA è la diagonale del rettangolo-casa di partenza (di cui conosciamo i lati a e b), il lato BI è uguale a d - b, il lato AI è uguale a d - a. Conoscendo i tre lati basta applicare la formula di Erone. Si calcola il semiperimetro p:
p = 1/2(BA + BI + AI) = 1/2(√(a2 + b2) + (d - b) + (d - a))
da cui l'area del triangolo ABI:
SABI = √(p (p - √(a2 + b2))(p - d + b)(p - d + a))
A questa dobbiamo togliere metà dell'area del rettangolo di partenza (ossia l'area di metà casa):
SBIAR = SABI - 1/2 ab
Passiamo ora ai due settori circolari BQI e API. Il loro raggio è ovviamente d - b e d - a, rispettivamente. L'area del settore circolare è data da:
settore = raggio2 · θ/2
Dove l'angolo θ è l'angolo al centro.
Nel nostro caso, noi conosciamo il raggio dei due settori, ma non l'angolo. Tuttavia, questo non è un problema... Riprendiamo il triangolo ABI e applichiamogli due volte la formula di Carnot (o del coseno), chiamando l'angolo BAI come α e quello ABI come β.
AI2 = BI2 + AB2 - 2BI · AB cos β
(d - a)2 = (d - b)2 + (a2 + b2) - 2 (d - b) √(a2 + b2) cos β
In questa espressione tutto è noto, per cui si può ricavare cos β e di conseguenza β.
Analogamente, si ricava α:
(d - b)2 = (d - a)2 + (a2 + b2) - 2 (d - a) √(a2 + b2) cos α
A noi, però, interessano gli angoli QBI e IAP. Nessun problema...
QBI = 180° - β - OBA
Ma OBA non è altro che l'arcotangente di a/b, per cui l'angolo QBI è noto.
Analogamente:
IAP = 180° - α - BAO
Ma BAO è l'arcotangente di b/a, per cui anche l'angolo IAP è noto.
Ne segue che i settori circolari hanno aree pari a :
SQBI = (d - b)2 · β/2
SIAP = (d - a)2 · α/2
con α e β espressi in radianti.
Concludendo: l'area brucata dalla capretta risulta essere:
STOT = 3 π d2/4 + SQBI + SIAP + SBIAR
Facciamo un caso pratico per avere un'idea migliore di quanto sia efficiente la nostra capretta. Immaginiamo che la casa abbia i lati di a = 20 m e b = 10 m. La corda d sia, invece, uguale a 50 m. Dopo aver fatto i calcoli si trova che:
STOT ≈ 7512. 2022 m2
Niente male davvero!
Altrettanto valido è il sistema utilizzato da Fabrizio, dove si elimina la parte contata due volte, ossia quella colorata in viola nella Fig. 5.
Riassumendo, l'area spazzata dalla capretta si si ottiene sommando queste parti:
(1) ¾ di cerchio di raggio d e centrato nel vertice della casa O
(2) ¼ di cerchio di raggio d-b, centrato nel vertice B
(3) ¼ di cerchio di raggio d-a e centrato nel vertice A
Le zone 2 e 3 sono, però, in parte sovrapposte proprio nella zona viola. Dobbiamo calcolare l'area di questa zona e toglierla dalla somma precedente.
La soluzione è chiaramente indicata da Fabrizio nel suo commento all'articolo del quiz.
Probabilmente ci sono anche altre soluzioni possibili (senza integrali)... se qualcuno le trovasse, ce lo faccia presente!
Il quiz lo trovate qui





