Questo è il quarto articolo della serie "La Relatività Generale al microscopio"

 

E' venuta l'ora di entrare in un... "campo" e, dato che è molto irregolare, vogliamo associare a ogni suo punto lo scostamento rispetto a un livello costante. In altre parole, associare a ogni punto il valore del campo. Lo facciamo a piccoli passi spostandoci di poco in ogni direzione. Alla fine otteniamo una "mappatura" tridimensionale perfetta. Ci accorgiamo che anche l'aggettivo "tridimensionale" perde di significato...

Abbiamo già usato la parola "campo" e sappiamo che esso esiste quando possiamo associare ad ogni suo punto (evento) una certa grandezza , sia essa uno scalare, un vettore o un tensore. Torniamo per un momento a un campo molto meno "matematico" e pensiamo a un bel campo di grano. Purtroppo, esso non è piano, ma pieno di rilievi ( colpa delle talpe?). Chi si trova nel campo può facilmente muoversi, ma a seconda della posizione che assume cambia l'altezza h (chiamiamola così per adesso) rispetto al livello più basso (se vogliamo, anche rispetto al livello del mare). Attraverso due coordinate ortogonali qualsiasi x e y, è possibile individuare la sua posizione P.

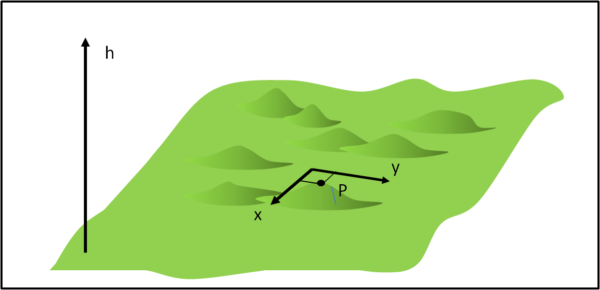
Immaginiamo, adesso, di far muovere P di un tratto estremamente piccolo. Come varia h? Tutto dipende dalla direzione in cui va P. Un certo versante della “collinetta” è decisamente più ripido di un altro versante. Stabiliamo perciò, al variare di P la variazione di h rispetto alle due coordinate x e y (Fig. 6).

P si muove, perciò, di dx lungo x e di dy lungo y. Introduciamo il concetto di gradiente. Non spaventiamoci: esso è praticamente una semplice derivata, ossia ci dice di quanto varia h al variare di x. Dato che stiamo parlando di percorsi molto piccoli indichiamo con  dx e dy i percorsi lungo x e y e con dh_x e dh_y le corrispondenti variazioni dell'altezza h. Il gradiente (ossia la ripidità del percorso nel piano x, h) è dato proprio dal rapporto dh/dx. Questo rapporto è esattamente la  tangente trigonometrica dell'angolo secondo cui è inclinata la componente del percorso di P nel piano (x, h), ossia la derivata di h fatta rispetto a x. La stessa identica considerazione possiamo farla nel piano (y, h) e ricaviamo un gradiente dh/dy.  Come possiamo allora scrivere la variazione dh_x nel piano (x,h)? Facilissimo:

dh_x = (dh/dx) dx

Infatti se il gradiente (ossia dh/dx) fosse, ad esempio uguale a 1/6 (h varierebbe di 1 metro se x variasse di 6 metri) e il percorso dx fosse uguale a 2 metri, la formula appena scritta ci direbbe che

dh_x = 1/6 · 2 = 1/3 m

ossia la variazione di h per un tragitto dx di 2 metri sarebbe pari a 1/3 di metro.

La stessa formula la possiamo applicare per ottenere la variazione di h al variare di y:

dh_y = (dh/dy) dy

Qualcuno potrebbe pensare di semplificare dx e dy nelle due formulette e ottenere  sia dh_x = dh che dh_y = dh.

Attenzione: il dx al denominatore può essere qualsiasi e indica solo di quanto varia x al variare di h, mentre il dx che moltiplica è proprio l'intervallo dx che ci interessa. Per non confondere le idee, meglio introdurre le derivate parziali... Anche qui, nessuna paura. Data una certa funzione in cui compaia sia x che y, si può benissimo calcolare la derivata della funzione rispetto alla sola x (considerando costante la y) e poi fare lo stesso per la derivata di h rispetto a y. Nel nostro caso la variabile h è funzione sia di x che di y: essa, infatti, varia sia variando x che variando y. Per cui è più giusto (e doveroso) scrivere al posto di dh/dx la notazione ∂h/∂x e al posto di dh/dy l'analoga ∂h/∂y. Le formule appena scritte devono perciò essere cambiate in:

dh_x = (∂h/∂x) dx

e

dh_y = (∂h/∂y) dy

Scritte in questo modo (decisamente più corretto) l'idea di semplificare ∂x con dx perde di significato. Idem per ∂y e dy. Notiamo che dx e dy sono rimasti tali e quali dato che loro sono sempre e comunque delle piccole lunghezze lungo l'asse x e l'asse y.

Come possiamo fare per stabilire la variazione totale di h dovuta a entrambi gli spostamenti (in x e in y)? Beh... molto semplice. Consideriamo dx e dy come due vettori. Lo spostamento finale è dato dal vettore ds che si determina con la solita regola del parallelogramma. Per sapere il valore finale della variazione di h per effetto di entrambi gli spostamenti in x e y, ossia per lo spostamento ds, basta sommare le variazioni dh_x e dh_y. Il tutto è mostrato in Fig. 7.  D'altra parte, invece di scendere direttamente lungo ds è sempre possibile prima scendere lungo dx e poi scendere lungo dy e si arriva sempre allo stesso punto, ossia si sono sommate le due variazioni di h dovute a x e a y (Fig. 7).

Possiamo, perciò, scrivere:

dh_s = dh_x + dh_y

ma, ricordando le due formulette precedenti, otteniamo:

dh_s = (∂h/∂x) dx + (∂h/∂y) dy

Questa formula ricavata in modo estremamente banale ci regala la variazione di h secondo qualsiasi direzione ds del nostro punto P.

Campo a n dimensioni 

Noi sappiamo che le coordinate dello spaziotempo sono quattro: x, y, z e t. No, non vogliamo portarci dietro lettere diverse che creerebbero molta confusione. Cambiamo un po' i simboli. h lo chiamiamo Φ e t, x, y e z li chiamiamo x⁰, x¹, x² e x³.

Attenzione: L'indice associato alle x non è un esponente, ma solo un indice per riconoscerle tra loro, pur dandole la stesso identica importanza, ed essere magari pronti ad aumentarne il numero, ossia a descrivere uno spaziotempo a 5, 6, ..., 10 dimensioni. Dal punto di vista puramente matematico non esiste nessun problema!

Scriviamo l'ultima formula in modo molto più serio e completo:

dΦ = (∂Φ/∂x⁰) dx⁰ + (∂Φ/∂x¹) dx¹ + (∂Φ/∂x²)dx² + (∂Φ/∂x³)dx³

o, in modo più stringato ancora:

dΦ= ∑_n(∂Φ/∂xⁿ) dxⁿ                         .... (1)

La formula rappresenta la variazione del valore del campo a seguito di una piccola variazione nello spaziotempo del punto-evento P.

Nota Bene: D'ora in poi cerchiamo di cambiare la visione comune degli assi cartesiani, in cui compaiono x, y, z e t. Quando scriveremo xⁿ (n = 4 per lo spaziotempo) indichiamo un intero sistema di coordinate x¹, x², x³,  x⁴, ..., xⁿ. Potremo, comunque, anche usare un sistema differente e chiamarlo yⁿ. Ricapitolando: l'indice n indica quale asse del sistema xⁿ si sta considerando, mentre l'utilizzo di y (ad esempio) indica che abbiamo cambiato sistema di riferimento, ossia vogliamo usare il sistema yⁿ, dove n indica nuovamente che asse si sta considerando nel nuovo sistema. Fondamentale è sapere come passare da un sistema all'altro, dato che vogliamo che il risultato NON dipenda dal sistema di riferimento.