Questo articolo è inserito in Meccanica Quantistica

Un metodo molto "rozzo" per descrivere cosa rappresenta realmente la sovrapposizione di stati quantici. Un metodo sicuramente noto ai... giocatori di golf!

Affrontiamo con un esempio terra-terra il problema della sovrapposizione quantica. Per far questo dimentichiamoci della dualità particella-onda così come dei veri stati di una particella quantica. Per far ciò prendiamo un elettrone e lo consideriamo proprio come una pallina. Ricordando un nostro lettore amante del golf, ipotizziamo che la nostra pallina possa avere una superficie liscia o una molto ruvida, proprio come quelle da golf. Queste due possibilità individuano due stati della pallina e chiamiamoli proprio "liscio" e "ruvido". Si intuisce facilmente che questa divisione vuole descrivere in modo semplificato i vari stati di un elettrone, come lo spin e cose del genere che noi vogliamo, però, dimenticare del tutto (per adesso, almeno).

In queste condizioni, cosa vuol dire che la nostra pallina si trova in una sovrapposizione di stati? Ogni tanto si legge che questa peculiarità significa che la pallina è contemporaneamente sia ruvida che liscia. No, questo non è vero. La pallina si trova SEMPRE in uno stato quantico UNICO. Teniamo anche presente che abbiamo ridotto le configurazioni di partenza a due stati, ma questi possono essere infiniti. Questa realtà dei fatti, però, complicherebbe enormemente la descrizione, per cui continuiamo con due soli stati. Ma qual è la differenza tra i due stati iniziali e un qualsiasi altro stato possibile? Per far questo, entriamo nel mondo dei vettori, anche se quelli con cui  abbiamo a che fare sono vettori molto particolari.

Immaginiamo una particella che si muova nello spazio. Essa possiede una certa velocità, ben definita, che non dipende dal sistema di riferimento che si utilizza. Possiamo ruotare a piacere il sistema cartesiano (x,y), ma la velocità finale della particella rimane sempre la stessa. Scegliamo, perciò a piacere i nostri assi x e y. I versori di questi due assi possiamo chiamarli versori di base. In questo spazio vettoriale la velocità della nostra particella può essere scomposta in una componente lungo x e in una lungo y. Attenzione, però, questi non sono veri vettori e la velocità è solo una grandezza che ci importa ben poco. Questi vettori rappresentano uno stato quantico e la scelta degli assi x e y ci indica le loro componenti lungo i due stati quantici che abbiano definito: quello "ruvido" e quello "liscio".

Il vettore "stato" può essere diretto comunque nello spazio dei vettori, ruotandolo attorno all'origine e variando la sua lunghezza. Tanto per rimanere con i piedi per terra, pensiamo a questo spazio come allo spazio immaginario, dove sappiamo che si può rappresentare molto bene la rotazione di un vettore. Per una ancora maggiore semplicità possiamo considerare il modulo del vettore che ruota uguale all'unità e, quindi, le sue componenti lungo gli assi (ruvido-liscio) saranno sempre minori o uguali a uno. Quando sono proprio "uno" siamo sicuri che la nostra pallina-particella è in uno stato base.

Pur considerando il modulo unitario, la rotazione del vettore-stato può dar luogo a infiniti stati, legati alla scelta dei nostri versori base. Questa situazione conferma in pieno quanto detto all'inizio: vi sono infiniti possibili stati, ma la particella deve essere sempre e comunque in un unico stato. Torniamo ad assumere lo stato come una velocità: il fatto che essa abbia due componenti lungo l'asse x e y non significa certo che essa possiede due velocità in un certo istante. Essa è sempre e comunque una certa velocità, assolutamente unica. Potremmo anche ruotare gli assi x e y come si vuole, ma la velocità rimarrebbe comunque in uno stato singolo, al limite potrebbe agire solo lungo uno dei due assi cartesiani.

Tornando alle nostre palline, essa potrebbe essere sia ruvida che liscia, ma anche in uno stato qualsiasi che associ allo stato della pallina due componenti lungo gli stati-base. In altre parole, di concetto molto più profondo: la particella ha un suo stato ben definito e ciò che può cambiare è solo la sua rappresentazione matematica. Allo stato della particella non interessa assolutamente quali sono le sue componenti lungo gli stati-base: la particella è quella che è, unica, sempre e comunque.

Facendo un piccolo salto nella matematica, possiamo anche indicare il nostro stato mediante le sue componenti lungo i due stati base, utilizzando una scrittura speciale:

x|ruvida> e y|liscia>

Il nostro vettore-stato si può, quindi, scrivere:

x|ruvida> + y|liscia>                                                    .... (1)

In pratica è una somma di vettori, tenendo però presente che ciò che è rappresentato da |> non è un vero vettore ma uno stato-base della pallina.

Siamo arrivati alla parte più critica della nostra avventura: la misura della nostra particella. Per ribadire ancora una volta il concetto che la misura non disturba lo stato quantico per la sua "intrusione" esterna, ma per fenomeni che sono solo delle particelle, costruiamo uno strumento di misura piuttosto semplice: una scatola in cui può entrare la nostra particella con il suo stato particolare, che ha però due fori di uscita, uno relativo alle palline ruvide e uno a quelle lisce. Cosa succede all'interno della scatola è del tutto indipendente da ciò che potremmo fare o "pensare" noi. Il meccanismo ci riporta, però, a due concetti che conosciamo già abbastanza bene: il principio di Heisenberg e la funzione d'onda di Schroedinger.

Non dobbiamo nemmeno spaventarci se parliamo di onde, dato che sappiamo benissimo che un'onda può essere rappresentata da un vettore che ruota nel piano complesso. Ma torniamo alla nostra pallina che è entrata nel misuratore o, se preferite, nel rivelatore di particelle. Essa ha solo due vie di uscita che permettono il passaggio solo a uno stato quantico, ruvido o liscio. Se la pallina è entrata liscia esce liscia; se è entrata ruvida esce ruvida. Facilmente, però, la pallina è entrata con uno stato quantico differente che è rappresentato dal suo vettore. Come esce, allora?  Una possibilità è che essa si divida in due parti corrispondenti alle componenti lisce e ruvide del suo vettore. No, questo non è possibile, la pallina non si può dividere. Ma, la pallina non può nemmeno restare all'interno del rilevatore! Non resta, allora, che una decisione basata proprio sulle sue componenti. Una facile operazione di prodotto scalare tra la (1) i due versori base, liscio e ruvido, porta a una scrittura del genere:

<ruvida|ruvida>  = 1

<ruvida|liscia> = 0 (i versori sono ortogonali)

Applicando la regola alla nostra pallina, abbiamo:

<ruvida|x|ruvida> + <ruvida|y|liscia>

x + 0

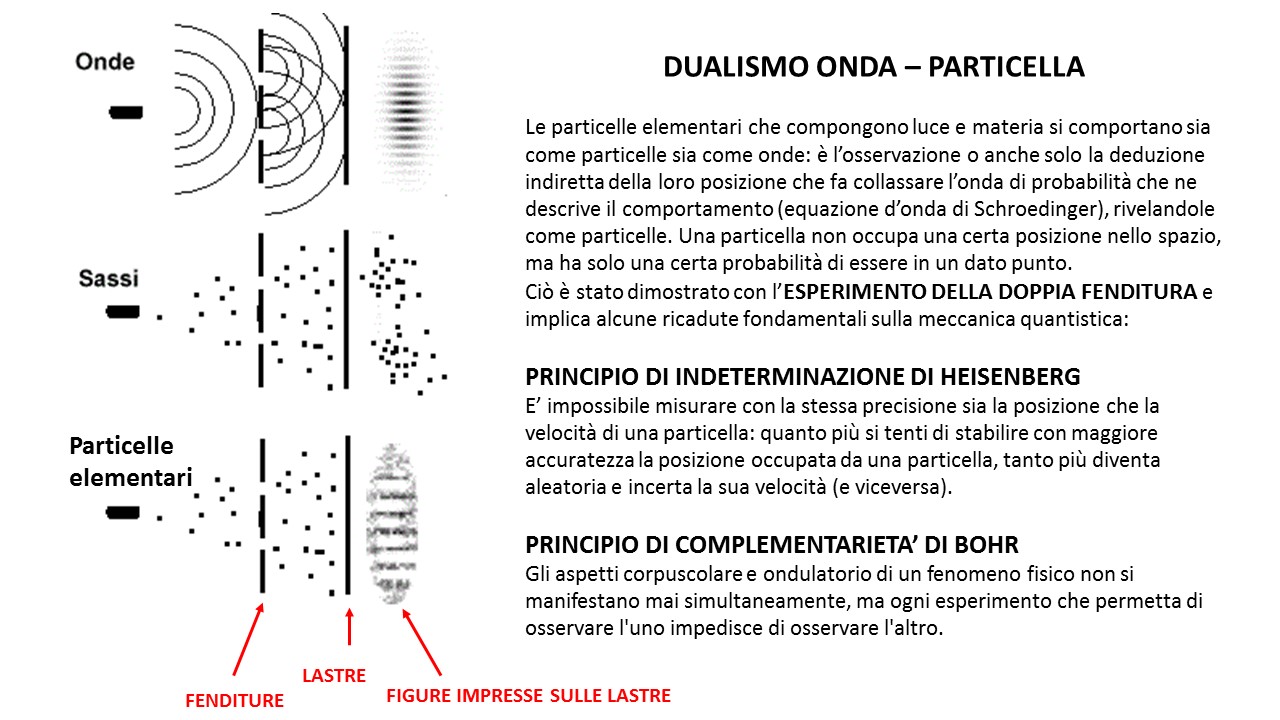
Il quadrato di questo numero (|x|²) ci dice la probabilità che ha la pallina di essere ruvida. Facendo la stessa operazione con l'altro versore (liscio)  si ottiene la probabilità che la pallina ha di essere liscia (|y|²). Non chiedetemi come fa il rilevatore a compiere tutto ciò. Al limite dovete chiedere ad Heisenberg e a Schroedinger... Non stupitevi nemmeno se il rilevatore assomiglia, in qualche modo, all'esperimento della doppia fenditura: vi posso assicurare che la somiglianza non è affatto casuale!

La nostra "favola" è finita, ma è doveroso ricordare che noi abbiamo usato solo due stati-base, mentre essi potrebbero essere infiniti.

In conclusione, questo racconto puramente metaforico, risponde alla domanda iniziale: una pallina può essere simultaneamente in più stati sovrapposti? No, assolutamente no. Essa può essere in uno degli infiniti stati del piano complesso. Al limite, la pallina ci può dire la probabilità che ha di essere rilevata come liscia o ruvida.