Categorie: Relatività
Tags: evento simultaneità simultaneità apparente simultaneità relativa sincronizzazione orologi sistema riferimento tempo assoluto tempo relativo velocità della luce
Scritto da: Vincenzo Zappalà
Commenti:8
La relatività speciale disegnata da Minkowski. 6: sincronizzazione e simultaneità ***
Siamo arrivati al punto fondamentale. Abbiamo enunciato i principi di una nuova teoria che estende la relatività galileiana all’intera fisica (e non solo alla meccanica) e stabilisce la costanza della velocità della luce. Adesso non ci resta che valutare ciò che essa comporta nella struttura spaziotemporale della realtà.
Prima di iniziare, però, dobbiamo essere sicuri di predisporre nel migliore dei modi un sistema di riferimento inerziale. Ricordiamo, infatti, che questa teoria non si occupa dei moti accelerati, ma solo dei sistemi in moto inerziale. Già così, però, vedremo che i concetti normali di spazio e tempo subiscono cambiamenti drastici.
Il punto più importante riguarda il tempo, inteso come una coordinata a tutti gli effetti e anch’essa da considerare una grandezza relativa e non assoluta. Per capire bene cosa implicano queste asserzioni, immaginiamo che due studenti vengano esaminati da una commissione al di fuori delle parti. Ciascuno di loro deve presentare il proprio progetto di sistema inerziale. Fatto questo, dovrà descrivere il moto di un punto all’interno del sistema così costruito. Questa specie di esame richiamerà ancora una volta i limiti della relatività galileiana e imposterà i capisaldi di quella einsteniana.
Uno strano esame
I due studenti hanno dei nomi molto indicativi: il primo si chiama Newton e il secondo Einstein (che fantasia!).
La commissione d’esame chiede a Newton di quali oggetti abbia bisogno per la sua rappresentazione. Per ragioni di estrema semplicità, immaginiamo che lo spazio sia a una sola dimensione. Newton sembra molto deciso: il suo sistema di riferimento è un segmento di retta nello spazio monodimensionale, abitato da tre punti (a, b e c). Inoltre, lo studente chiede un’asta rigida di lunghezza costante ben determinata, che chiama “metro”. Infine, domanda un ottimo orologio, che scandisca i “secondi”, ben visibile da qualsiasi punto del suo segmento che funge da sistema di riferimento.
A questo punto inizia la costruzione del sistema. a e b sistemano l’asta rigida in modo che il suo bordo sinistro coincida con l’inizio del segmento. Il punto d’inizio viene chiamata spazio s = 0. Il punto finale dell’asta rigida viene chiamato spazio s = 1. c controlla che tutto venga eseguito alla perfezione. a e b sistemano ora l’asta in modo che il suo bordo sinistro coincida con s = 1. Il bordo destro viene chiamato s = 2. Il procedimento continua fino alla fine dello spazio a disposizione sul sistema di riferimento.
L’unico orologio a disposizione viene inserito nel centro del segmento, per controllare meglio l’ora esatta, ma potrebbe essere messo ovunque.
Ovviamente, asta, abitanti dello spazio e orologio non si potrebbero vedere, avendo una sola dimensione, ma noi li abbiamo evidenziati per seguire meglio il procedimento.
E’ ora di descrivere il moto di c che parte dal punto 0 e si muove verso a e b, che controllano posizione e tempo. Per ragioni di semplicità, c si muove di moto costante (ma poteva fare qualsiasi cosa). Quando inizia il suo movimento, l’orologio segna 0 secondi. Come giunge nel punto 1, l’orologio segna 5 secondi, e via dicendo fino a raggiungere il punto 3 quando l’orologio segna 15 secondi. Newton non ha problemi a descrivere il moto di c, come si vede in Fig. 13.
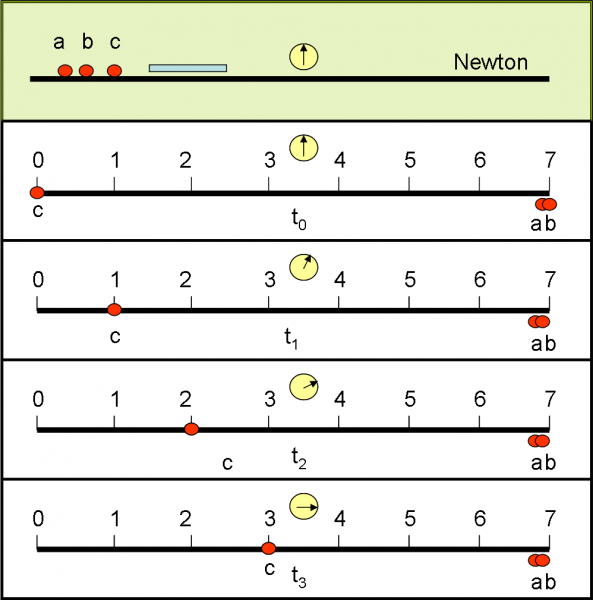
Nel caso scelto si tratta di un moto rettilineo uniforme eseguito con una velocità costante u = 1/5 = 0.2 m/sec. Come già detto, il tipo di movimento di c è del tutto ininfluente e può essere qualsiasi, dato che si svolge all’interno del sistema di riferimento. Quello che sarà veramente importante nel prosieguo dell’esame è che TUTTO il sistema di riferimento si muova di velocità v costante rispetto alla commissione d’esame.
La commissione mormora qualcosa e chiede a Newton quale sia la ragione che l’ha spinto a usare una sola asta e un solo orologio. Newton sorride e risponde : “Il tempo è assoluto e uguale per tutti. Una lunghezza rimane la stessa in qualsiasi sistema di riferimento si sia. Segnata la divisione dello spazio essa non cambia più ”. La commissione invita Newton a ritirarsi. Newton si sente molto tranquillo, dato che è sicuro che anche la commissione ha visto esattamente ciò che hanno visto i punti a e b in movimento insieme al segmento. D’altra parte sa bene che qualsiasi legge della meccanica si descrive nello stesso modo se i sistemi di riferimento sono inerziali.
Descriviamo in modo più rigoroso la legge del moto che si è verificata nel sistema di riferimento in movimento. Essa collega una serie di eventi capitati su di esso. Il primo è stato “la presenza di c nel punto 0, all’istante 0”. Il secondo, “la presenza di c al punto 1, all’istante 5 secondi”, e via dicendo. La legge del moto va quindi considerata non solo come una variazione di spazio, ma come una successione di eventi. In altre parole come una funzione s(t), dove ogni si(ti) rappresenta un evento.
Bene, anche noi siamo pienamente d’accordo con questa visione della realtà e ci ricordiamo lo spazio-tempo disegnato da Newton basandosi sulla relatività galileiana.
Tocca ora a Einstein. Egli chiede le stesse cose di Newton, ma vuole tutta una serie di orologi e di aste rigide. Inoltre chiede una lampadina che possa accendersi e spegnersi, ovviamente. Fa sistemare da a e b le aste, una davanti all’altra a partire dall’inizio del segmento-spazio. Gli orologi sono posti uno per ogni punto di contatto tra le aste.
Einstein dice anche che, prima di iniziare l’esperimento, a, b e c devono eseguire una procedura che serve per fare in modo che gli orologi segnino tutti veramente la stessa ora, una volta che siano posti nella loro posizione; in poche parole, gli orologi devono essere sincronizzati perfettamente.
Einstein afferma, infatti, che per definire un evento ha bisogno della posizione di chi sta muovendosi, ma anche del tempo corrispondente misurato da un orologio che sia posto esattamente nel punto in cui si trova il corpo che si muove. Descrive, in modo analogo a Newton, la legge del moto con la funzione s(t) dove ogni si(ti) rappresenta un evento in cui, però, l’orologio -ripetiamolo ancora- deve essere posto nel luogo in cui si trova, istante per istante, il corpo in movimento. Anzi, preferisce dire che un evento è rappresentato dalla coppia di coordinate (si,ti). Il tutto è rappresentato in Fig. 14.
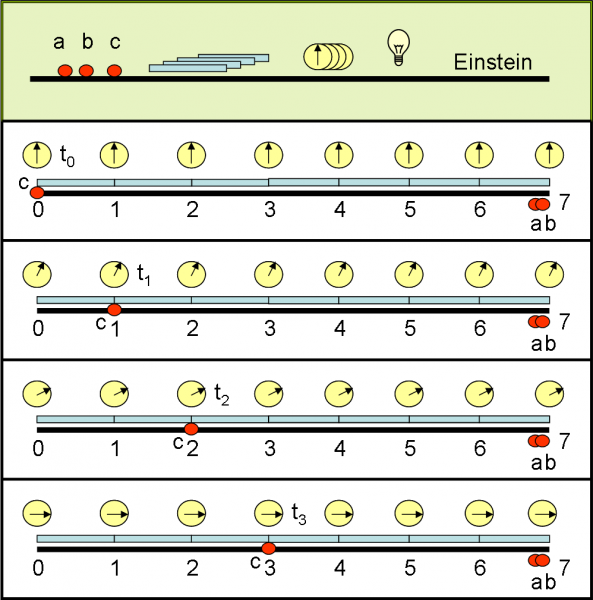
La commissione d’esame sembra approvare con maggiore enfasi, mentre Newton è convinto che Einstein abbia fatto la stessa identica cosa che ha fatto lui. Anzi, l’uso di tanti orologi può aver reso imprecisa la misura degli eventi. Nel suo mondo, trovare due orologi che segnano lo stesso tempo è un bel problema.
La commissione chiede a Einstein: “Perché hai lasciato le aste e gli orologi al loro posto?”. Einstein risponde che ha bisogno di avere sempre a disposizione un sistema sicuramente ben determinato per non mandare in confusione il segmento e i suoi abitanti quando saranno visti da un altro sistema di riferimento. Almeno localmente, bisogna avere delle certezze (e sorride) e il reticolo di lunghezze e orologi, così costruito, assicura che il sistema sia sempre lo stesso, qualsiasi cosa dicano gli altri…
Newton non è certo uno stupido e comincia a intuire che tutto quel lavoro di Einstein non è sicuramente stato un puro divertimento. Da un momento all’altro, si aspetta qualche novità che non aveva previsto.
Sembra che la commissione gli abbia letto nella mente. Infatti gli chiede: “Potresti dirci come faresti a sincronizzare tutti quegli orologi?” Newton non ha problemi a rispondere: “Niente di più semplice. Porto tutti gli orologi nel punto O, inserisco perfettamente la stessa ora e poi li trasporto nei vari punti di lettura degli eventi. Vorrei, però, ribadire che tanto valeva che mettessi un solo orologio bene in evidenza…”.
La stessa domanda viene fatta a Einstein. Egli risponde, molto gentilmente, che quanto proposto da Newton può anche andare bene, ma gli orologi devono essere trasportati molto lentamente, dato che per muoversi e per fermarsi devono subire una accelerazione e una decelerazione. Niente può assicurargli che durante questa manovra l’ora che un orologio segna alla fine del trasporto rimanga la stessa di quella che avrebbe segnato se fosse rimasto fermo in 0. Lui preferisce una procedura più sicura e accurata.
Newton è sempre meno sicuro di sé, mentre la commissione è estremamente interessata.
Sincronizziamo gli orologi
Einstein fa sistemare gli orologi nella loro posizione, senza curarsi tanto di ciò che segnano. Poi dice una frase molto indicativa: “Se potessimo creare un segnale che viaggiasse a velocità infinita, esso impiegherebbe un tempo uguale a zero per raggiungere tutti gli altri orologi. Porrei a in 0 e b in 1. a metterebbe la lancetta sullo zero e contemporaneamente manderebbe il segnale a b che istantaneamente sistemerebbe anche le lancette del secondo orologio sullo zero. Poi si sposterebbero su 1 e 2 e ripeterebbero la procedura fino a sincronizzare anche il numero 7.
A quel punto sarei sicuro che tutti gli orologi del sistema inerziale segnerebbero la stessa ora e continuerebbero a segnarla. Purtroppo, non abbiamo a disposizione un segnale che viaggia a velocità infinita e ci dobbiamo accontentare del segnale più veloce che possediamo: il segnale luminoso.
Sappiamo che la luce non viaggia a velocità infinita, ma soltanto a 300 000 km/sec (anzi poco meno). La fortuna è, però, che la velocità della luce è una costante per qualsiasi sistema di riferimento. Questa costanza diventa fondamentale”. Newton ha ormai le idee veramente confuse e comincia a capire che la sua visione della realtà è troppo semplicistica. Einstein invita gli abitanti del suo sistema di riferimento a proseguire con l’operazione di sincronizzazione.
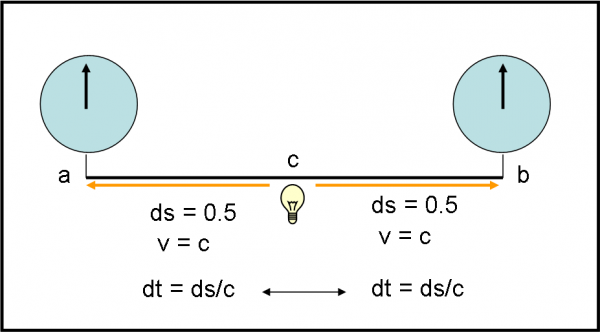
a si mette in 0 e b in 1. c, invece si pone esattamente a metà dell’asta che congiunge 0 con 1. Non hanno certo problemi a misurare il punto di mezzo, dato che è una semplice misura spaziale. c, che si trova in s = 0.5 prende in mano la lampadina. Poi, avvisa i compagni e l’accende. A questo punto Einstein tira fuori la sua carta vincente (ampiamente dimostrata) che dice che la velocità della luce è indipendente dal sistema di riferimento usato e che è la stessa in qualsiasi direzione vada (isotropia dello spazio). Può quindi essere sicuro che la luce percorre spazi uguali in tempi uguali ed è sempre uguale a c, comunque si muova il sistema di riferimento. Ne consegue che la luce arriva in 0, dove si trova a, e in 1, dove si trova b, nello stesso istante (gli spazi sono uguali e quindi anche il tempo impiegato).
All’arrivo della luce, a e b fanno partire i loro orologi che DEVONO segnare lo stesso tempo. L’orologio in 0 e quello in 1 sono sincronizzati. La semplice operazione è riassunta in Fig. 15.
Per sincronizzare gli altri orologi è solo questione di pazienza e precisione. Ad esempio, possono fare come riportato di seguito. a si sposta in 1 e b si sposta in 2, così come c si sposta tra 1 e 2, in 1,5. Accende di nuovo la lampadina. A questo punto, a, che vede girare il proprio orologio sincronizzato con quello di 0, prende nota della differenza di tempo tra il tempo segnato dall’orologio e quello di arrivo della luce, che considera come un nuovo tempo zero. Sia esso un certo dt. Questo è un valore sicuramente corretto dato che tutte le misure sono state svolte nello stesso luogo e con lo stesso orologio. b, invece, ha fatto partire l’orologio in 2 (lancetta rossa). Attende che a lo raggiunga (poco importa il tempo che ci mette) e gli comunica il valore dt. b non deve fare altro che aggiungere dt all’ora che segna la lancetta rossa e ottiene la lancetta nera che è per definizione sincronizzata con quella dell’orologio in 1 e, quindi, anche con quello in 0. La Fig. 16 mostra questa procedura.
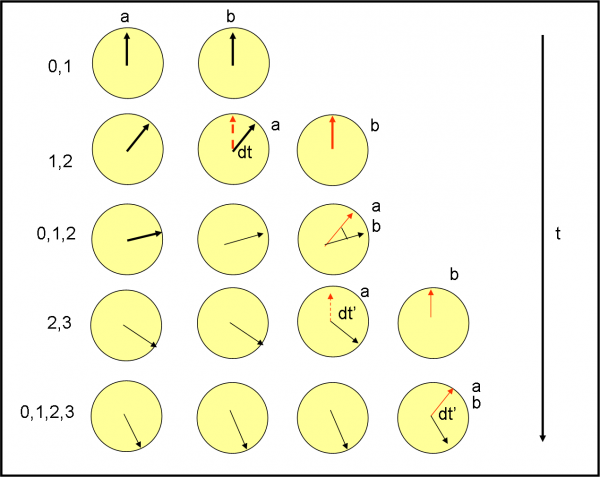
Basta ripetere l’operazione e tutti gli orologi del sistema di riferimento sono sincronizzati, ossia essi segnano sempre lo stesso tempo, indipendentemente dal moto del sistema. Notiamo, ancora una volta, che tutto ciò è stato possibile perché la velocità della luce è una costante.
Il tempo assoluto di Newton subisce un duro colpo e, dato che lo studente è decisamente intelligente, capisce già che la sua teoria si sta sgretolando come un castello di carte colpito da una raffica di vento. E’ costretto ad ammettere che Einstein ha ragione, dato che la costanza della velocità della luce è stata dimostrata. Si siede ed è estremamente interessato a vedere cosa impone questa nuova visione della realtà. Gli stessi professori fanno silenzio e invitano Einstein a proseguire. L’esame è terminato e ora tutti desiderano solo imparare!
Da questo momento in poi, perciò, affrontiamo tutti assieme la teoria della relatività ristretta. Se pensiamo che finora sono state dette delle banalità, stiamo molto attenti! E’ essenziale digerire bene il procedimento eseguito e ricordare sempre le condizioni di partenza della nuova avventura.
Cosa significa simultaneità?
Il punto di arrivo di tutta questa sceneggiata preliminare si riferisce alla simultaneità di due eventi. L’evento “luce che arriva in 0” e quello “luce che arriva in 1” sono eventi simultanei, dato che gli orologi in 0 e 1 sono stati sincronizzasti. Non dimentichiamolo!
Nella relatività galileiana il concetto di simultaneità è assoluto, qualsiasi sia il sistema di riferimento, dato che il tempo è assoluto. In altre parole, se due eventi accadono nello stesso momento in un sistema di riferimento, lo devono fare in qualsiasi altro sistema di riferimento. Nella relatività ristretta ciò non è più vero e il sistema di riferimento appena costruito da Einstein ce lo dimostra molto chiaramente.
Eseguiamo, quindi, un esperimento atto proprio a mostrare la relatività della simultaneità di due eventi. Questo è un fatto normalmente trascurato in molte trattazioni. A prima vista sembrerebbe del tutto inutile, una volta che si sono acquisiti i concetti della dilatazione dei tempi e della contrazione delle distanze (ecco perché Einstein ha voluto che nel sistema di riferimento ci fosse un reticolo spaziotemporale ben determinato). E’, invece, un fatto che va studiato indipendentemente anche se, ovviamente, è collegato strettamente alle ripercussioni più famose che vedremo in seguito.
Non lo possiamo trascurare, dato che sarà estremamente importante quando passeremo alla rappresentazione grafica di Minkowski. Per cui, mi raccomando, cerchiamo di capire bene il profondo significato di ciò che Einstein ci sta per mostrare.
Prima di proseguire, è bene porre attenzione all’utilizzo della parola "osservatore", che viene spesso usata nella relatività. Sembrerebbe impossibile e invece può portare a gravi fraintendimenti. Per questo motivo è bene ribadire, una volta per tutte, cosa si deve intendere con la frase "osservatore in un riferimento S ". Con tale frase non si deve intendere una singola persona ma, in realtà, un riferimento, ad ogni punto del quale siano associate tre coordinate x,y,z (noi spesso ne useremo una sola, la s), che ne individuano la posizione spaziale (in altre parole, proprio l’insieme di aste rigide che hanno usato i nostri amici a, b e c) e un insieme di orologi sincronizzati fra di loro, posti nei vari punti dello spazio.
Non trascuriamo questa definizione, anche se a prima vista sembrerebbe ridondante e inutile. Lo stesso Einstein l’ha descritta nei dettagli e nessuno può credere che si divertisse ad aggiungere cose superflue alla sua teoria.
Anche la simultaneità è relativa
Va bene, iniziamo, introducendo finalmente un osservatore esterno al nostro sistema di riferimento abitato da a, b e c. Osservatore esterno, vuol dire sistema di riferimento con tanto di orologi sincronizzati e punti definiti spazialmente da tante aste rigide. Questo nuovo sistema lo possiamo chiamare S’, mentre quello precedente lo chiamiamo S. Dato che entrambi sono stati “preparati” adeguatamente è del tutto analogo considerarne uno fermo e l’altro in moto o viceversa: sappiamo ormai benissimo che il movimento può essere solo relativo e non esiste un sistema di riferimento assoluto. L’unica cosa di assoluto è la costanza della velocità della luce.
Per eseguire l’esperimento sicuri di noi stessi, chiediamo nuovamente al sistema S (ossia ad a, b e c) di mostrarci senza ombra di dubbio che abbiano eseguito perfettamente quanto richiesto da Einstein.
Cambiamo solo leggermente le condizioni di partenza, ma il succo rimane lo stesso. Diamo una lampadina ad a e una a b, posti ai due bordi opposti del sistema. c occupa, come sempre, il punto di mezzo. Alla stessa ora a e b accendono la loro lampadina (ognuno si fida del suo orologio che sa essere perfettamente sincronizzato con quello dell’amico). Come era del tutto prevedibile, c riceve la luce esattamente allo stesso istante (anche il suo orologio è sincronizzato e quindi deve segnare la stessa ora di quello di a e di b). A c non resta che concludere che l’evento “accensione della luce di a” e “accensione della luce di b” sono eventi simultanei. La Fig. 17 mostra questo esperimento che è del tutto simile a quello che era servito per sincronizzare gli orologi di S. Il risultato è quindi del tutto ovvio, ma è sempre meglio non fidarsi mai… (come vedremo tra poco).
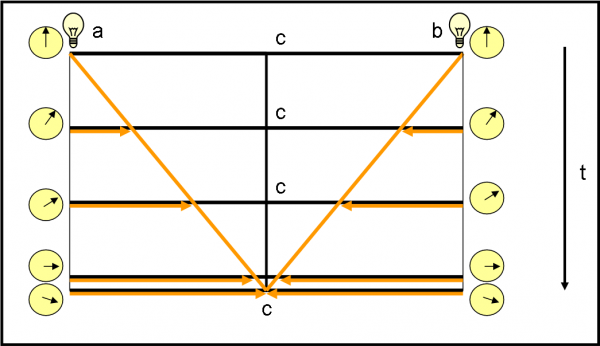
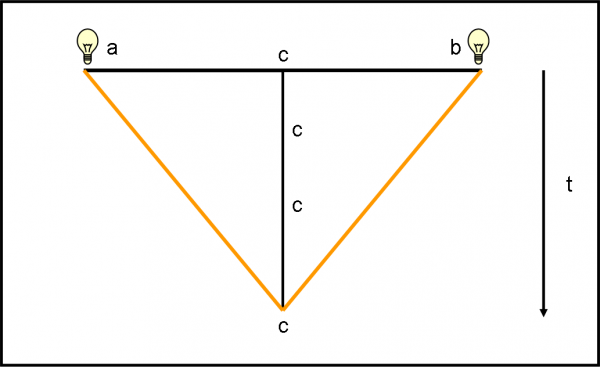
Abbiamo fatto scorrere il tempo verso il basso e di tanto in tanto abbiamo disegnato il punto di arrivo della luce partita da a e b nello stesso istante. Un espediente un po’ infantile che possiamo sintetizzare nella Fig. 18, utilizzando solo le linee diagonali che individuano i punti raggiunti dalla luce istante per istante. Ovviamente le due diagonali si incontrano in c nello stesso istante. Scusate la pedanteria, ma è meglio camminare molto lentamente ed essere ridondanti.
Introduciamo il nuovo sistema S’, in cui ci può essere uno, due, cento osservatori. Poco importa, dato che anche in questo sistema tutto è stato predisposto perfettamente, con le aste rigide e gli orologi sincronizzati. Disegniamo la Fig. 19.
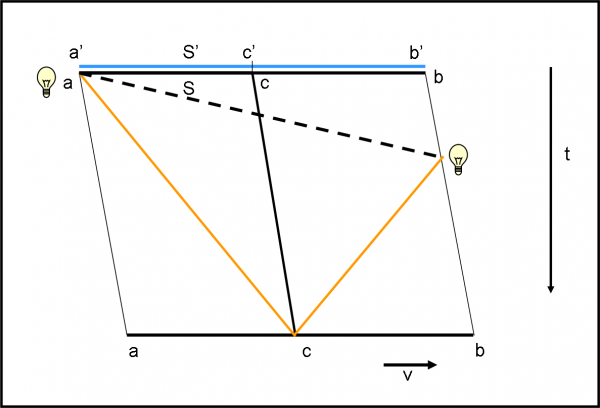
I sistemi S e S’ coincidono al momento dell’ipotetica accensione delle due lampadine in a e b. Siano a’, b’ e c’ gli osservatori di S’ che coincidono in quell’istante con a, b e c.
Tuttavia, il sistema S si muove rispetto a S’. La luce, invece, viaggia sempre nello stesso modo ed è del tutto indipendente dal sistema in cui la lampadina è stata accesa. Essa quindi deve seguire due linee diagonali esattamente come prima (la loro inclinazione deve essere la stessa). Il signor c deve essere raggiunto nello stesso istante sia dalla luce inviata da a sia da quella inviata da b. Tuttavia per ottenere questo risultato, all’osservatore S’ risulta ovvio che a deve aver acceso la lampadina PRIMA di b. Non vi è altro modo perché la luce che viaggia sempre con la stessa velocità sia per S che per S’ giunga nello stesso istante in c . Per S' non è assolutamente vero che a e b abbiano acceso la lampada nello stesso istante: i due eventi, “a accende la lampada” e “b accende la lampada”, non sono simultanei!
D’altra parte, questa conclusione non è difficile da ottenere con il ragionamento. La luce di a deve percorrere uno spazio maggiore per arrivare a c di quello che deve percorrere la luce di b. Dato che la luce viaggia sempre alla stessa velocità, per percorrere uno spazio maggiore bisogna che la lampada si accenda prima. Se su S sono convinti di avere sincronizzato gli orologi si sbagliano di grosso. Infatti, l’orologio in a e quello in b segnavano la stessa identica ora quando le lampade si sono accese. Ma, per S’ risulta chiaro che i due eventi non sono simultanei e quindi gli orologi non sono sincronizzati.
In breve, gli abitanti di S dicono che le due lampade si sono accese simultaneamente e che i loro orologi sono sincronizzati. Gli abitanti di S’ dicono invece che la lampadina di a si è accesa prima di quella di b, ossia che l’orologio di a va avanti rispetto a quello di b! Possiamo anticipare (ma ci servirà, e come!, per la rappresentazione di Minkowski) che la simultaneità nel sistema S, vista nel sistema S’, è data dalla linea tratteggiata.
Possiamo anche descrivere, in Fig. 20, il problema in modo leggermente diverso (ognuno scelga quello che preferisce).
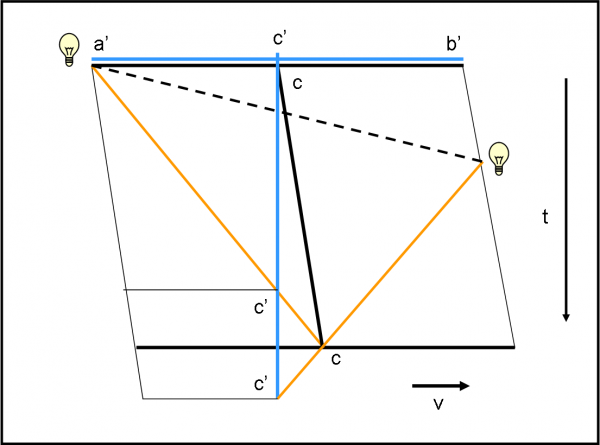
Siamo nelle stesse condizioni di prima, con S che dice di essere sicuro di avere sincronizzato i suoi orologi. Lo stesso dice S’. a e b accendono la loro lampadina e la luce comincia a viaggiare come prima. Cosa si aspetta S’? Beh, dato che S gli ha detto che le due lampade si sono accese simultaneamente, la loro luce deve raggiungere il signor c’ nello stesso identico tempo. D’altra parte, la luce è partita in corrispondenza di a’ e b’, quando coincidevano con a e b. E se è partita simultaneamente per a e b, lo stesso deve anche valere per a’ e b’, anch’essi con gli orologi sincronizzati! Ne consegue che la luce deve raggiungere contemporaneamente c’.
a’ e b’ fanno in fretta a capire che S’ ha detto una falsità (almeno per loro). Infatti, è abbastanza evidente che quando la luce emessa da a arriva in c, insieme a quella di b, essa è già passata da c’, mentre quella partita da b deve ancora arrivarci. Se è già passata da c’ vuol dire che ha già raggiunto il punto di mezzo, dove avrebbe dovuto incontrare quella di b, se le lampadine fossero partite in simultanea (per S’). Invece la luce di b deve ancora raggiungere c’ (ha appena raggiunto c). L’unica conclusione possibile è che la luce di b sia partita dopo quella di a (o -se preferite- quella di a è partita prima di quella di b).
In realtà hanno ragione sia gli osservatori di S che quelli di S’. La verità è che il concetto di simultaneità di eventi separati spazialmente dipende dal sistema di riferimento in cui si osserva.
Notiamo, infatti, che stiamo trattando con eventi che si riferiscono a due punti diversi dello spazio (a e b).
Facciamo ancora un piccolo ragionamento che anticipa quello che troveremo. Se nel sistema S le lampadine si accendono nello stesso istante, vuole anche dire che i due orologi posti in a e b segnano lo stesso tempo (ta = tb). Ma, se nel riferimento S’ gli eventi appaiono non simultanei, gli orologi posti a terra nei punti a’ e b’ segnano tempi ta’ e tb’ diversi fra loro e, quindi, almeno uno dei due tempi deve differire da quelli misurati dagli orologi in a e b. Il tempo segnato dagli orologi non è, perciò, un tempo assoluto ma è relativo al sistema di riferimento.
E’ importante notare che, secondo questo ragionamento, i due sistemi S e S’ sono del tutto equivalenti. Potevamo agire al contrario, piazzando le lampade su S’ in a’ e b’ e accenderle simultaneamente (ta’ = tb’)). In questo caso, se a e b sono i due punti di S che coincidono con a’ e b’ al momento dell’accensione delle lampadine, i tempi di accensione misurati su S (ta e tb) devono apparire diversi.
Simmetria
Questa perfetta simmetria deve già farci riflettere. Non abbiamo trovato che solo uno dei due sistemi ha sincronizzato male i suoi orologi, ma che entrambi sembrano aver sbagliato la sincronizzazione se visti dall’altro sistema. Non vi è una variazione in un particolare sistema, ma una variazione che dipende solo e soltanto da quale sistema si osserva. Il lungo procedimento usato da Einstein per fissare con sicurezza lo spaziotempo in qualsiasi sistema di riferimento ci dà una perfetta garanzia che niente può cambiare nel singolo sistema di riferimento, ma cambia solo la sua apparenza se visto da un altro. Viene ribadito ancora una volta che non vi è un sistema di riferimento assoluto.
Scusate la pedanteria, ma facciamo un piccolo passo in avanti. Se il tempo in S variasse veramente e, per esempio, scorresse più lentamente, in S dovremmo vedere quello di S’ scorrere più velocemente. Invece, ciò che si osserva è che il anche il tempo di S’ scorre più lentamente se visto da S. Questa perfetta simmetria garantisce che il tempo può anche cambiare ma solo in relazione al sistema scelto per osservare. Il tempo è quindi grandezza relativa. Altrimenti accetteremmo l’esistenza di un tempo assoluto.
Non anticipiamo, però, il futuro. Il vero problema è che la dilatazione del tempo di un orologio in movimento, e l’accorciamento di un’asta, fanno parte della consueta trattazione della relatività ristretta e non necessitano di un grande sforzo mentale per essere compresi. Lo stesso non capita per la relatività della simultaneità. E’ un concetto molto più difficile da “digerire”. Essa dice, in sintesi, che non vi è una relazione assoluta tra i tempi relativi a due eventi che si riferiscono a luoghi distanti tra loro.
Un esempio terra-terra, anzi terra-luna. Immaginiamo di avere due alberi di Natale, uno a Parigi e uno a Los Angeles. Predisponiamo tutto affinché essi si accendano alla stessa ora nel sistema Terra. Non è difficile ottenere questo risultato. Noi siamo contenti di esserci riusciti, ma, nel frattempo, un osservatore sulla Luna, che si muove rispetto alla Terra, dice che abbiamo fallito!
Simultaneità apparente
Attenzione, però, a non confondere questa relatività della simultaneità con la simultaneità apparente di due eventi che capitano normalmente nella nostra vita quotidiana. Consideriamo la Fig. 21.
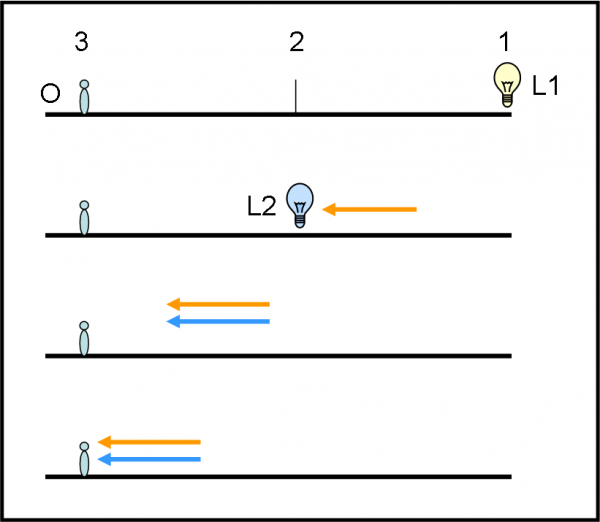
P è un osservatore fisso situato nel punto 3. A un certo istante t1 si accende la lampadina gialla nel punto 1. Quando la sua luce arriva nel punto 2 (al tempo t2), si accende anche la lampadina azzurra. La luce gialla e azzurra adesso viaggiano insieme e raggiungono l’osservatore allo stesso istante t3. P conclude che l’accensione delle due lampadine è stata simultanea, dato che la loro luce arriva nello stesso istante. E’ la stessa cosa che capita quando accendiamo una lampadina a due metri di distanza e abbiamo la fortuna di vedere esplodere nello stesso istante una supernova a 20000 anni luce, oppure quando sentiamo, contemporaneamente, il segnale orario della radio sul tavolo e il segnale inviato dalla sonda Rosetta (sperando che sia reso di dominio pubblico).
Tuttavia, la simultaneità è solo apparente, dato che le due lampadine si sono realmente accese in luoghi diversi nel sistema di riferimento di P. Lui considera come istantaneo solo l’evento che avviene in 3 e giudica simultanei anche gli eventi avvenuti in 1 e in 2. Ciò non è vero! Prima di giudicare la simultaneità dell’evento a cui ha assistito, egli deve controllare gli eventi avvenuti in 1 e in 2. Si accorgerebbe che le lampadine sono poste a distanze diverse da lui e quindi deve tenere in conto della maggiore distanza percorsa dalla luce 1 rispetto a quella di 2. Solo dopo aver eseguito la correzione può veramente parlare di eventi realmente simultanei nel suo sistema di riferimento!
Non per niente nei casi precedenti abbiamo sempre considerato eventi che raggiungono un luogo posto a metà strada tra le loro posizioni. In tal modo abbiamo evitato qualsiasi simultaneità apparente, dato che le distanze da percorrere sono esattamente le stesse. Ancora una volta, lo strano reticolo, costruito da Einstein sul sistema di riferimento, appare come un fatto tutt’altro che infantile!
Quantità relative
Abbiamo scoperto una nuova “quantità” che si aggiunge a quelle relative. Richiamiamole, anche se alcune devono ancora essere introdotte: non possiamo sapere se una nave spaziale si muove di moto rettilineo uniforme rispetto a un’altra oppure sta ferma; non possiamo stabilire se un’asta è lunga un metro come non possiamo concludere se un certo fenomeno dura un minuto: questi valori sono veri solo in un particolare sistema di riferimento. A questa piccola lista possiamo adesso aggiungere che non si può stabilire in modo assoluto se due eventi, lontani tra loro, siano simultanei. O -ma è la stessa cosa- se due orologi posti a una certa distanza sono sincronizzati tra loro. Nuovamente, ciò può essere vero solo per un sistema di riferimento, ma non per un altro.
Mi raccomando, evidenziate subito qualsiasi dubbio o possibile errore abbia commesso (mi capita spesso…). I concetti descritti fin qui devono essere compresi perfettamente prima di proseguire.






8 commenti
Bah, caro Enzo, hai fatto diventare simpatico perfino l'antipaticissimo (a quanto ne so) Newton; poverino, lo hai messo a confronto con un ... caterpillar!
Ho iniziato a leggere la serie di Minkowski e prometto solennemente di non ... scassare fino al tuo ritorno.
povero Isacco... in fondo era sempre da solo nella sua infinita ... genialità!!! Avesse avuto un compagno di giochi come Albertino o Riccardo... chissà che "giochi" avrebbero fatto assieme!!!!
Che dire, Enzo, sono piombato con grande ritardo su questa serie di articoli e tra ieri e oggi li ho letti e capiti tutti senza fare grande fatica: penso sia la prima volta che un argomento di fisica mi appaia tanto semplice. Vedremo se riuscirò a non incepparmi con i prossimi ...
magnifico Massimo!
Mi raccomando: al minimo dubbio bloccami subito... vorrei arrivare fino alla fine con la stessa semplicità e chiarezza. Se necessario, riscriverò le parti che potrebbero risultare un po' ostiche. Ma la simultaneità è già un bel banco di prova!
Caro Enzo spero di aver compreso davvero fino in fondo questo articolo, poiché solleva questioni tutt'altro che banali.
Innanzitutto, quando Einstein chiede di sincronizzare gli orologi, se non ho capito male, tiene conto del tempo che impiega la luce, infatti “a” annota tutti i tempi (dt) che usa ogni volta per sincronizzare l'orologio successivo.
In pratica deve tener conto del “ritardo” dovuto alla velocità finita con cui viaggia l'informazione (la luce).
Innanzitutto sia il sistema S, che il sistema S', hanno eseguito la medesima procedura per sincronizzare gli orologi, ognuno ha tarato i suoi strumenti mentre viaggiava ad una certa velocità, ossia nel proprio sistema di riferimento inerziale.
La figura (molto simile a quella dell'articolo... scusate, però per me costruire da zero una figura serve per verificare se ho davvero compreso il suo significato e per analizzarla da diverse angolazioni), sottostante mostra cosa vede S dal suo punto di vista (in fin dei conti S potrebbe tranquillamente ritenere di esser fermo e che sia S' a muoversi):
http://www.astrobin.com/full/78662/P/
Quando, però, S' tenta di applicare il suo tempo, tarato in un sistema inerziale che si muove a velocità diversa da S, succede quello che mostra Einstein:
http://www.astrobin.com/full/78662/Q/
Nella figura, ho evidenziato alcune cose (avrei preferito fare la figura con il tempo che scorre verso l'alto, ma poi ho pensato che così avrei rischiato di confondere le idee a chi legge).
La velocità della luce è costante per qualunque sistema di riferimento, per cui la sua retta deve avere sempre la stessa inclinazione (nel disegno 45°).
Per C la luce di A e B arriva contestualmente, nel suo sistema la taratura è stata effettuata alla solita costante velocità di crociera di S.
Per C', invece B non può che aver acceso la luce più tardi, tanto che prima viene raggiunto dalla luce di a e poi da quella di b.......
E' evidente che gli orologi di S (pur essendo sincronizzati fra loro) non sono affatto sincronizzati con quelli di S' (i cui orologi sono sincronizzati fra loro).
Piccola domanda vedendo la situazione dal punto di vista di S', ho evidenziato anche l'ipotetica posizione della lampadina accesa da b al “tempo zero”...... oltre a non tornare i conti con il tempo mi sembra che non tornino nemmeno con lo spazio, o sbaglio?
In ultimo ho evidenziato con una linea verde, quella che dovrebbe indicare la simultaneità e penso di aver intuito perché a da cosa possa dipendere (rapporto tra velocità di allontanamento di S da S' e velocità della luce?
Dico, questo, perché se si pone la velocità di S rispetto a S' uguale a ½ di quella della luce, lo “sfasamento” tra i due sistemi è ben più ampio
http://www.astrobin.com/full/78662/R/
Spero di aver capito almeno in parte il ragionamento proposto, oppure ho commesso qualche errore di di impostazione?
Paolo
PS dopo la figura 19 c'è una frase: “Per S non è assolutamente vero che a e b abbiano acceso la lampada nello stesso istante: i due eventi, “a accende la lampada” e “b accende la lampada”, non sono simultanei! ”... penso sia per S' e non per S.
caro Paolo,
mi sembra che tu abbia capito perfettamente e ti ringrazio per la correzione alla svista... C'avrei giurato di lasciare un apice indietro o di metterne uno di troppo (forse dovevo chiamarli S e R...). Dici anche molto bene che la lunghezza deve cambiare. Tra non molto vedremo proprio come gli orologi sembrano andare in modo diverso e come le lunghezze si accorciano a seconda del sistema di riferimento. Ma sarà sicuramente tutto più facile... te lo assicuro!
Credo di aver capito anche io il concetto di fondo di simultaneità dell’articolo.
Mi mette un po’ più in difficoltà però capire il funzionamento geometrico della figura 19 e del significato della linea tratteggiata S. ) anche sul significato dei segmenti aa’ e bb’…
) anche sul significato dei segmenti aa’ e bb’…
Sembra un elemento fittizio o comunque estraneo ai sistemi S e S’…
Ho qualche dubbio (sono un po’ imbarazzato a dirlo visto che a occhio sembrerebbe facile capirlo
Questi segmenti rappresentano la funzione che lega tra loro i 2 sistemi (e quindi i punti evento dei due sistemi) in funzione dello scorrere del tempo e della loro velocità di allontanamento (indipendentemente da quale sia il sistema che si muove rispetto all’altro visto che non è determinabile)?
In questo caso, se i segmenti aa’ e bb’ raggiungessero un’inclinazione > 45 gradi (che dovrebbe comportare una velocità di allontanamento tra i due sistemi maggiore di quella della luce) dovrei ritrovarmi nella situazione di non vedere più la lampada A e, a seconda di quanto è grande l’inclinazione, in alcuni casi neanche la lampada B nel sistema di riferimento S’?...
Se il funzionamento è più o meno corretto allora il segmento S tratteggiato e dato solo dai punti in cui il cono di luce di C interseca i segmenti aa’ e bb’ che rappresentano soltanto i punti eventi percorsi nel tempo e nello spazio dal sistema S’?
In questo caso verrebbe confermato che è un qualcosa di fittizio e non esistente in quanto il sistema S’ non vede nella realtà gli eventi (accensione lampada A e B) avvenire simultaneamente e la linea tratteggiata mi da solo un’idea di quanto si è “deformata” in S’ la simultaneità che si ha invece in S…
Mamma mia che fatica, spero di non aver riempito lo spazio tempo di questo blog di sciocchezze!

Articolo un po' tirato per le lunghe per il concetto da spiegare ma comunque chiaro alla maggior parte credo.
Bravo Enzo!