Categorie: Relatività
Tags: contrazione delle lunghezze lunghezza propria relatività ristretta sincronizzazione trasformazione di Lorentz
Scritto da: Vincenzo Zappalà
Commenti:4
La relatività speciale disegnata da Minkowski. 11: tesoro, mi si sono ristretti i ragazzi! **
Partendo dalla trasformazione di Lorentz l’effetto di contrazione delle lunghezze diventa un fenomeno estremamente interessante -e semplice- dal punto di vista della logica. Gli orologi sistemati in un sistema di riferimento e sincronizzati come spiegato alcuni articoli fa (QUI), permettono di afferrare perfettamente l’effetto della contrazione della lunghezza di un’asta rigida in movimento rispetto al sistema in cui si effettua la misura.
Consideriamo la Fig. 1. In alto abbiamo un sistema S’ di origine O’. Su di esso non abbiamo bisogno di usare orologi sincronizzati, dato che abbiamo già stabilito la lunghezza effettiva di un asta rigida. La sua lunghezza è L0 = x2’ – x1’. Come detto, può essere misurata tranquillamente attraverso il metro campione che è solidale con il sistema.
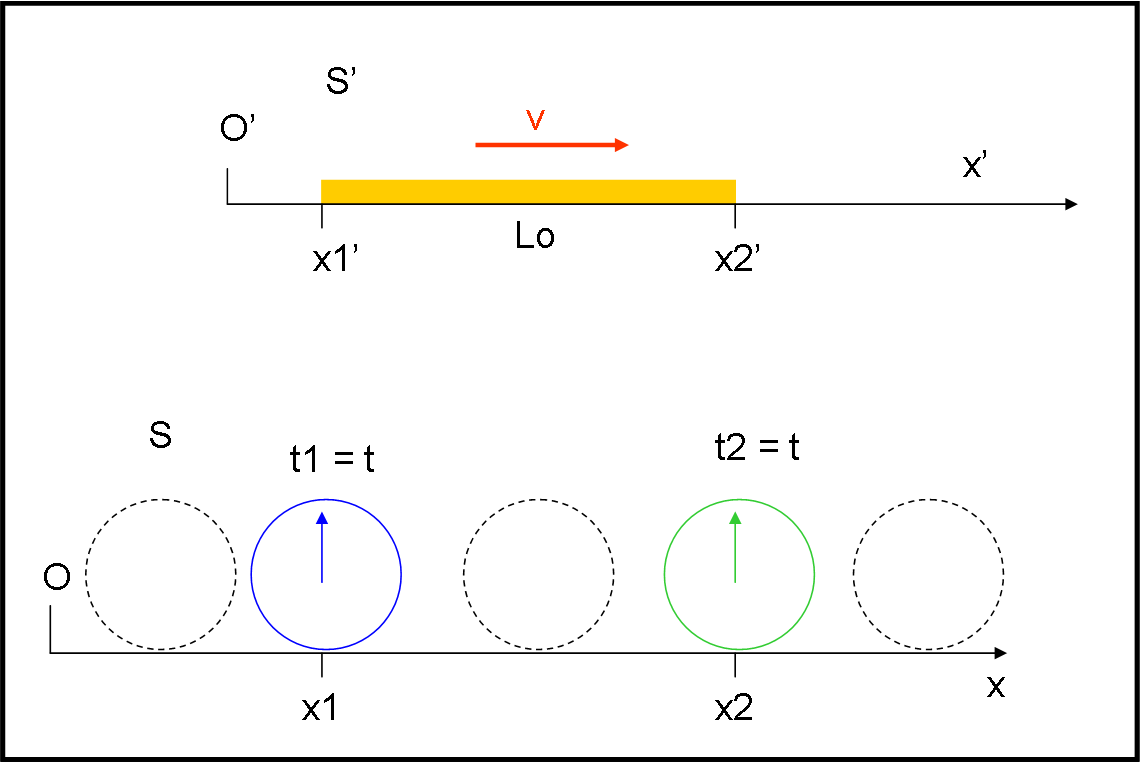
Mettiamo in moto il sistema S’ con velocità v rispetto a un sistema S di origine O. Lungo tutto il sistema S sono posti orologi sincronizzati, che quindi segnano la stessa ora. Per misurare la lunghezza dell’asta basta utilizzare i due orologi che vedono passare i due estremi dell’asta nello stesso istante t. Se gli orologi sono ovunque ciò è sempre possibile, dato che esiste sicuramente un orologio che è posto esattamente nel punto in cui passa il limite sinistro e uno che è posto esattamente nel punto in cui passa il limite destro dell’asta in movimento con S’. Le posizione di questi due orologi siano x1 e x2, nel sistema S. Ovviamente, per come è stato effettuata la misura, t1 = t2 = t.
A questo punto, non ci resta che considerare la prima delle equazioni della trasformazione di Lorentz, quella che lega x a x’.
x’ = (x – vt)/(1 – v2/c2)1/2
Applichiamola alla posizione dei due estremi dell’asta. Nel sistema S’, la posizione dell’estremo sinistro è x1’, mentre nel sistema S è x1. L’estremo destro ha ascisse x2’ e x2, rispettivamente. Il tempo misurato in x1 e x2, come già detto, deve essere lo stesso, per definizione, ossia t1 = t2 = t. Nell’equazione non compare assolutamente il tempo t’ misurato su S’ (la misura della lunghezza L0 non ne ha avuto bisogno). La velocità di S’ rispetto a S sia, come al solito, v.
x1’ = (x1 – vt)/(1 – v2/c2)1/2
x2’ = (x2 – vt)/(1 – v2/c2)1/2
Sottraendo la prima equazione dalla seconda, si ha:
x2’ – x1’ = (x2 – x1)/(1 – v2/c2)1/2
Ma x2’ – x1’ è proprio la lunghezza L0 dell’asta, misurata in S’, mentre x2 – x1 è la lunghezza L dell’asta, misurata da S:
L0 = L /(1 – v2/c2)1/2
Ossia:
L = L0/γ …. (1)
Essendo 1/γ sempre minore di 1, possiamo concludere che la lunghezza di una asta in movimento con velocità v rispetto a un sistema S, viene “contratta” se misurata da S. La contrazione avviene nella direzione del moto.
Dobbiamo notare che anche questa volta c'è una differenza sostanziale fra L0 e L. Infatti, L0 rappresenta la lunghezza dell’asta misurata nel riferimento in cui essa è ferma. La sua lunghezza viene misurata confrontandola con il metro campione e non ha bisogno di nessun orologio.
Non confondiamoci, mi raccomando. Se la stessa asta fosse stata messa nel sistema S, la sua lunghezza sarebbe rimasta L0, dato che sarebbe ferma in questo sistema. L0, quindi, rappresenta la lunghezza di un asta, in qualsiasi sistema essa venga posta, a patto di misurarla in quel sistema. Questa lunghezza, similmente a quanto fatto per il tempo, viene chiamata lunghezza propria (o a riposo). L, invece, è una misura effettuata mentre l’asta si muove, utilizzando due orologi posti in posizioni diverse, anche se sincronizzati. L rimane quindi influenzata dalla sincronizzazione degli orologi effettuata su S, ossia nel sistema in cui è misurata.
Proprio per il principio di relatività, essendo i due sistemi equivalenti, se la stessa asta viene posta nel sistema S, l’osservatore che si muove con velocità v arriva alla stessa identica conclusione, ossia la lunghezza dell’asta appare contratta come dice la (1).
Ricavata in questo modo, la contrazione delle lunghezze diventa di estrema ovvietà. A patto di aver utilizzato i postulati di Einstein per scrivere la trasformazione di coordinate.
Non vi è ovviamente bisogno di ripetere che la contrazione avviene solo nella direzione del moto, dato che abbiamo già dimostrato che la y e la z non subiscono alterazioni. L’altezza di un asta appare sempre la stessa a qualsiasi velocità vada rispetto a un altro sistema di riferimento.






4 commenti
Enzo, ma possiamo dire che la trasformazione di Lorentz (1897) è una logica conseguenza dei postulati di Einstein... Ricordo di aver letto (?) che la trasformazione di Lorentz era una conseguenza dell'esperimento di Michelson-Morley. Potrei tranquillamente ricordare male
No, no Gaetano,
la trasformazione di Lorentz nasce già prima per spiegare in qualche modo le leggi di Maxwell che vanno contro la relatività galileiana. Einstein ne approfitta e le usa proprio per i suoi scopi. Lorentz sapeva fare la trasformazione ma non spiegava il perché. Einstein le ricava utilizzando i suoi postulati e quindi fornendo il perché...
Caro Enzo, questa volta un po' per misurare la contrazione delle lunghezze, un po' per diletto, mi sono divertito a costruire e provare a risolvere un piccolo QUIZ.
Per far ciò ho chiesto aiuto ai nostri amici papalliani (che di quiz se ne intendono), confidando nel loro aiuto....
Sul pianeta Papalla un papalliano si considera in forma quando assume la forma di perfetta di una sfera di raggio 0,5 metri.
Visto di lato un papalliano sembra quindi un cerchio dal diametro di 1 metro.
Non tutti i papalliani però sono in perfetta forma ed alcuni visti di lato assomigliano più ad un ellisse che non a un cerchio.
L'altezza non cambia, ma la larghezza si amplia ed addio rotondità.
La figura mostra tre papalliani, uno in perfetta forma e gli altri due un po' meno.
http://www.astrobin.com/full/38903/J/
Visti di lato (due dimensioni) Papallo A è un cerchio perfetto, Papallo B pur rimanendo alto 1 metro ora misura 1,2 metri in larghezza (asse maggiore dell'ellisse), anche l'altezza di Papallo C è rimasta di 1 metro ma il suo asse maggiore misura 1,5 metri.
Quando i papalliani cercano di far colpo sulle papalline, tendenzialmente cercano di sembrare in perfetta forma.
Papallo A non è molto preoccupato di ciò, ma Papallo B e Papallo C non demordono ed entrambi si ricordano del racconto dei due saggi: PapalLorentz e PapallAlbert.
Fortunatamente i papalliani sanno esser molto veloci (non come i fotoni, però son pieni di risorse nascoste), per cui Papallo B e Papallo C decidono di correre velocissimi affinché il loro asse maggiore torni ad assomigliare al diametro del cerchio sintomo di perfetta forma.
Ovviamente l'altezza non cambia ed i Papalliani son furbi e fanno coincidere il loro asse maggiore con l'ipotetico asse x dei Papalliani fermi che osservano).
http://www.astrobin.com/full/38903/K/
A quale velocità rettilinea uniforme devono andare Papallo B e Papallo C per sembrare in forma?
Quasi, quasi mi fermo qui e fornisco le soluzioni nel prossimo post (certo che se poi i presupposti e le soluzioni del quiz sono errati .).
.).
Innanzitutto conviene fissare le condizioni per mostrarsi in perfetta forma.
L'asse maggiore di Papallo B misura 1,2 metri, e quello di Papallo C misura 1,5 metri, per cui:
Papallo B: Lo (b)= (x2' -x1') = 1,2 metri
Papallo C: Lo (a) = (x2' -x1') = 1,5 metri
Entrambi vorrebbero apparire in perfetta forma, ossia con l'asse maggiore che diventa nuovamente un diametro perfetto di 1 metro, per cui.
L = (x2 -x1) = 1 metro
Fissate le condizioni, basta trovare il fattore di Lorentz (ossia l'entità delle deformazioni spaziotemporali), corrispondente:
L= Lo/γ
γ = Lo/L
Quindi, Papallo B: γ = 1,2/1 = 1,2
Papallo C: γ = 1,5/1 = 1,5
Ricavato il valore di γ per trovare la velocità, conviene innanzitutto ricavare il valore di β, ossia del rapporto v/c.
γ = 1/(1-β^2)^1/2
γ^2 = 1/(1-β^2)
1-β^2 = 1/γ^2
1 = 1/γ^2 +β^2
β^2= 1- 1/γ^2
β= (1- 1/γ^2)^1/2
Sostituendo:
Papallo B
β= (1- 1/(1,2)^2 )^1/2
β= (1- 1/(1,44 )^1/2
β= (1- 0,694)^1/2
β= 0,5527
Papallo C
β= (1- 1/(1,5)^2 )^1/2
β= (1- 1/(2,25 )^1/2
β= (1- 0,444)^1/2
β= 0,7453
Tradotto in velocità:
β= v/c
v = β c
Papallo B
v = (0,5527) 300.000 km/sec = 165.831 Km/sec
Papallo C
v = (0,7453) 300.000 km/sec = 223.606 Km/sec
La cosa più divertente è che sia Papallo B, sia Papallo C mentre correvano vedevano i papalliani fermi, che di solito sembravano in forma, come svuotati, una specie di ellisse in cui questa volta l'asse maggiore è rappresentato dall'altezza.
Ovviamente una volta tornati a velocità meno impegnative i loro assi tornano alle solite dimensioni (possono solo sperare che tutta l'energia consumata per raggiungere simili velocità abbia migliorato il peso forma).
Se v= 0, β= v/c = 0
Se β= 0, γ =1
Se γ =1, L= Lo/γ = Lo
Ops, dimenticavo una piccola appendice.
Entrambi i Papalli sono passati per l'orologio del paese ed hanno fatto partire le lancette dei loro cronometri.
I papalliani sono dotati di una fitta rete di orologi sincronizzati (controllati da telecamere), anche nei dintorni del pianeta (a certe velocità i papalli possono tranquillamente finire nello spazio intorno al pianeta).
Trascorso 1 secondo di tempo papaplliano, viene rilevata (da due orologi diversi) la posizione di Papallo A e Papallo B.
Per gli orologi sincronizzati con il pianeta Papalla è trascorso 1 secondo, ma quale tempo segnano in quell'istante, secondo i guardiani degli orologi, i due cronometri di Pappallo B e Papallo C (t2'-t1')?
http://www.astrobin.com/full/38903/L/
Dato che si conoscono i valori del fattore di Lorentz γ dovuti alle rispettive velocità dei due Papalli e si conosce anche l'intervallo di tempo papalliano trascorso(quello misurato dagli orologi sincronizzati):
Δt = (t2 – t1)= 1 secondo.
Δtp = t2’ – t1’ =?
Δt = Δtp γ
Δtp = Δt /γ
Sostituendo i valori di γ corrispondenti ai due Papalli:
Papallo B
Δtp = 1/1,2 = 0,833 secondi
Papallo C
Δtp = 1/1,5 = 0,666 secondi
Ovviamente, dato che si conoscono le velocità rettilinee uniformi dei due Papalli, è semplicissimo ricavare la distanza dei due orologi che hanno rilevato la loro presenza dopo 1 secondo di tempo (per il pianeta Papalla):
s=vt, dove t= 1 secondo
Papallo B
v = 165.831 Km/sec
S= 165.831 Km
Papallo C
v = = 223.606 Km/sec
S= 223.606 Km
Spero di non aver detto troppe sciocchezze e che il quiz sia piaciuto.
Paolo
magnifico Paolo!


Non solo hai dimostrato di aver capito perfettamente la trasformazione di Lorentz, ma hai raccontato un'avventura papalliana meravigliosa
Penso proprio che nella versione completa della relatività speciale il tuo racconto verrà inserito come esempio, insieme ai mesoni di cui parleremo tra non molto. In fondo anche i mesoni (dicono...) sono originari di Papalla...
I complimenti si sprecano... (domani mattina, comunque, controllo bene i calcoli... non si sa mai, ma il procedimento è perfetto)...