Categorie: Relatività
Tags: dinamica relativistica quantità di moto relatività ristretta
Scritto da: Vincenzo Zappalà
Commenti:21
Dinamica Relativistica.1 : Cambiamo la quantità di moto. 3
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo
Immaginiamo adesso di applicare la RR al secondo caso (applicarla al primo non avrebbe senso dato che non vi è movimento relativo). Respiriamo a lungo, riassumiamo mentalmente ciò che abbiamo acquisito e… proseguiamo. Non dimentichiamo che tutte le velocità osservate dal sistema S’ rimangono sempre uguali a quelle disegnate nella Fig. 3. Il sistema S’ non si sente assolutamente diverso. Sono le sue velocità viste da S che cambiano a causa del moto di S’. Queste velocità viste da S sono, perciò, colorate in rosso. Rappresentiamo il fenomeno (che deve risultare sempre lo stesso dato che qualsiasi fenomeno fisico deve rimanere lo stesso in qualsiasi sistema inerziale) nella Fig. 5 che rimpiazza la Fig.4.
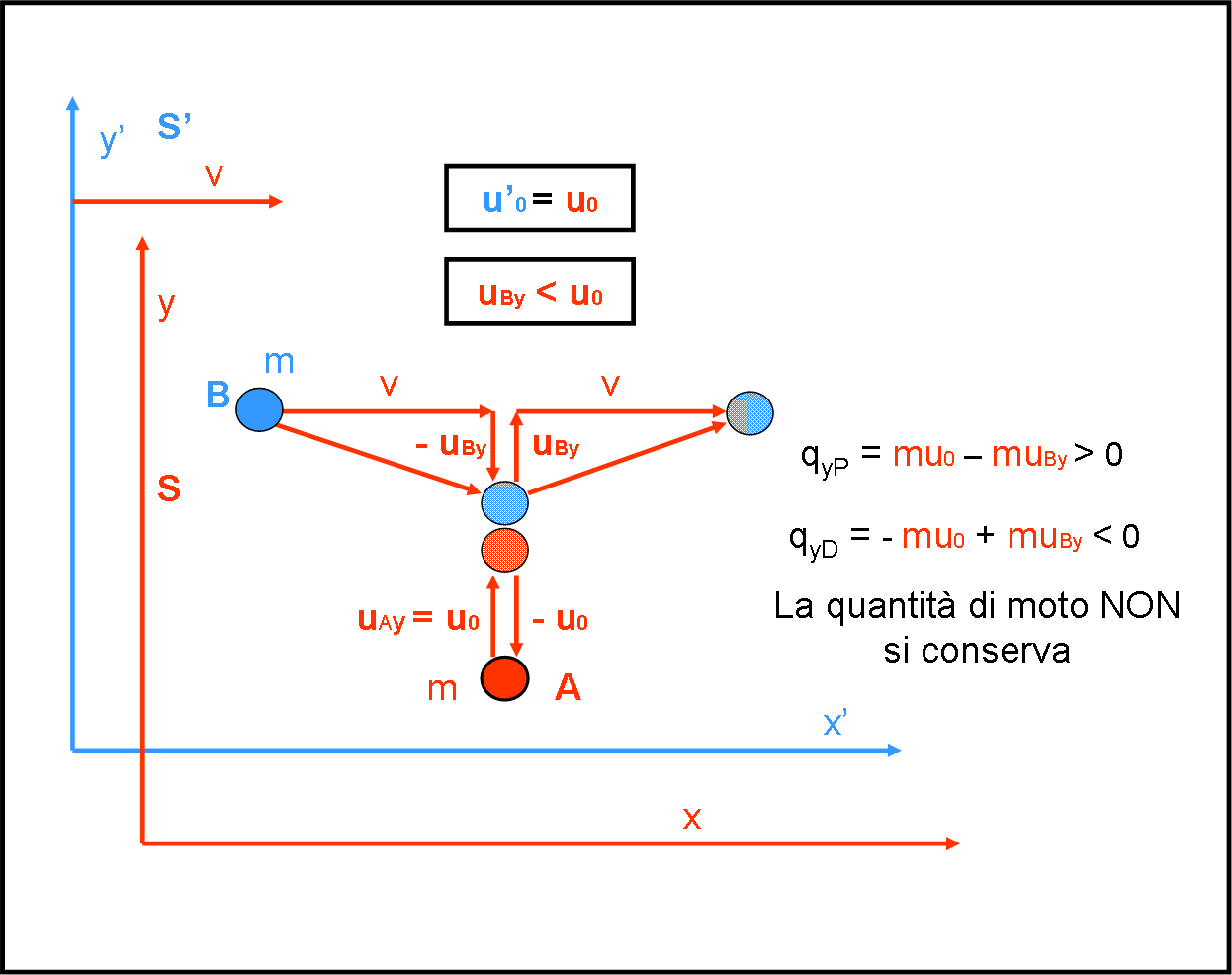
A prima vista potremmo pensare che non è cambiato niente. E, invece, qualcosa è cambiato. La v rimane la stessa dato che è quella che è e si riferisce a S (è solo lui che la “vede”), ma la componente verticale rossa della velocità della pallina blu vista da S (che chiamiamo per comodità uBy) è più piccola di quella del caso precedente. Non dobbiamo certo stupirci, dato che la velocità ortogonale alla direzione del moto, subisce un accorciamento come ricordato fin dall’inizio.
Possiamo riscrivere la formula (2) per la componente prima dell’urto:
- uBy = - u’By (1 – v2/c2)1/2/(1 + v u’Bx/c2)
Abbiamo solo cambiato gli indici (e il segno), per applicarla al nostro esperimento.
Anche se non possiamo eseguirlo praticamente nel testo, pensiamo che le componenti che hanno l’apice si riferiscono al sistema S’ e dovrebbero essere scritte in blu.
Tuttavia, possiamo eseguire delle semplificazioni. u’By non è altro che uBy, la componente della pallina blu vista da S, ossia l’originale u0. Nel sistema di riferimento S’ la velocità è sempre la stessa. Inoltre, u’Bx non è altro che la componente orizzontale della velocità u0 vista da S’. Ma questa è ZERO, dato che la pallina blu in S’ non si muove assolutamente in orizzontale!
La formula di prima si trasforma nella (3) che, applicata al nostro caso, come dovevamo aspettarci, dà:
- uBy = - u0(1 – v2/c2)1/2 …. (4)
Non ci resta che calcolare la componente verticale della quantità di moto totale qP, prima dell’urto. Per analogia, la velocità della pallina A (rossa) può anche essere scritta uAy, pur sapendo che essa vale sempre u0.
Quella della pallina rossa (A), rimane sempre la stessa, ossia muAy = mu0. Quella della pallina blu vista dal sistema S deve fare uso della (4). In conclusione abbiamo:
qPy = muAy - muBy = mu0 - m u0 (1 – v2/c2)1/2 > 0
Notiamo, infatti, che la seconda parte è SICURAMENTE più piccola della prima parte, dato che la stessa quantità è stata moltiplicata per un numero minore di uno (la radice quadrata).
Calcoliamo, adesso, la componente verticale della quantità di moto totale qD, dopo l’urto.
Per la pallina rossa, abbiamo - muAy = - mu0, per la pallina blu, abbiamo muBy (si ha completa simmetria prima e dopo l’urto), da cui:
qDy = - muAy + muBy = - mu0 + m u0 (1 – v2/c2)1/2 < 0
Per essere ultra pignoli e ripetitivi, stiamo aggiungendo, a una certa quantità negativa, la stessa quantità (positiva) moltiplicata per un numero minore di uno. Il risultato deve essere una quantità minore di ZERO.
Purtroppo, dobbiamo ammettere che la quantità di moto verticale non si conserva. D’altra parte sappiamo già che quella orizzontale si conserva e quindi non possiamo che concludere che la quantità di moto totale non si conserva nell’urto!
Cambiare o non cambiare? Questo è il problema…
Abbiamo di fronte una situazione imbarazzante e non banalissima… Potremmo scegliere una via d’uscita decisamente comoda: accettare il fatto che la quantità di moto non si conserva nella RR e … buonanotte a tutti! Tuttavia, la non conservazione della quantità di moto comporterebbe la non conservazione di molte altre grandezze. La fisica ne sarebbe stravolta…
No, siamo troppo seri per fare una cosa del genere e dobbiamo seguire quanto fatto, con grande ragionevolezza, da Einstein: dobbiamo proprio cambiare definizione dalla quantità di moto, in modo che:
1) Essa si conservi anche nella RR
2) Per velocità molto piccole coincida con la definizione classica






21 commenti
Per tutti papalli,
 se non ho frainteso il ragionamento, prendendo palalucciole per papallanterne, se parto dalla pallina A:
se non ho frainteso il ragionamento, prendendo palalucciole per papallanterne, se parto dalla pallina A:
qP = muAy - muBy = mu0 - m u0 √(1- v²/c²) > 0
Affinché la quantità di moto si conservi, basta dividere la massa per √(1- v²/c²)
muAy = m u0
se divido m/√(1- v²/c²)
muAy = m u0/√(1- v²/c²)
Vista da S la pallina A ha solo una velocità lungo l'asse y, quindi v=0:
muAy = m u0/(1 – 02/c2)1/2 = m u0/1 = m u0
La velocità della pallina blu, vista di S, invece risente delle deformazioni relativistiche, per cui anche la componente y della velocità della pallina cambia a causa della diversa misura del tempo
muBy = m u0√(1- v²/c²)
se divido m/√(1- v²/c²)
muBy = m u0√(1- v²/c²)/ √(1- v²/c²) = m u0
Ne segue che considerando la massa come variabile, ossia la sua misura effettuata da un sistema S “fermo” sembra subire anch'essa una deformazione relativistica a velocità prossime a quelle della luce (m/ √(1- v²/c²), si riesce a conservare la quantità di moto:
qP = muAy - muBy = mu0 - m u0 = 0
Se parto dalla pallina Blu.
qD = - muAy + muBy = - mu0 + m u0 √(1- v²/c²) < 0
qD = - muAy /√(1- v²/c²) + muBy/√(1- v²/c²) = - mu0 + m u0 = 0
Sempre che tutto ciò sia corretto... penso di aver intuito cosa si intende per massa a riposo e massa relativistica ... ma ....
... ma .... 
Paolo
Attenzione Paolo!
La massa relativistica deve dipendere dalla velocità a cui viaggia il corpo e NON dalla velocità relativa tra i due sistemi.
La velocità di A non è uguale a zero, ma è uguale a uAy = u0... Idem per quella di B che è ben più grande essendo la composizione di v e di -uby... A ogni massa la sua correzione.
Tu, in pratica, hai considerato la massa di A a riposo, mentre lei si muove con velocità uo e hai considerato quella di B come essere solo v, ma ciò non è vero! Un doppio errore fa tornare il risultato...
Non possiamo correggere solo le masse che vogliamo: la massa deve essere corretta in base alla sua velocità vista da un sistema di riferimento.
Tu scrivi:
qD = - muAy /√(1- v²/c²) + muBy/√(1- v²/c²) = - mu0 + m u0 = 0
ma questo indica che la massa viene divisa per la stessa quantità e non per qualcosa che dipende dalla velocità delle singole masse osservata da S!
Stai proprio facendo l'errore di cui parlavo all'inizio: ogni massa deve essere corretta sulla base della sua velocità e non della velocità tra due sistemi di riferimento (o almeno non solo di quella...). Il risultato torna, ma è sbagliato il concetto di correzione. Questo è un errore che compiono moltissime spiegazioni che vedi sul web...
Cari tutti,
Paolo ha messo in evidenza l'errore più sottile e comune che viene fatto nella dinamica relativistica. Superato questo piccolo scoglio concettuale, tutto diventa poi molto più facile e intuitivo! E' l'unico vero e pericoloso scoglio che si trova prima di poter nuotare verso la celebre formula....
Ha volte gli errori sono più utili di tante spiegazioni
caro Paolo,
ancora un piccolo aiuto per capire l'errore... Tu hai corretto la massa di A indipendentemente dalla sua velocità, ma sulla base del movimento di S'. E cosa faresti alla massa di A se non esistesse nessun sistema S'? Anche se andasse molto veloce tu la considereresti sempre come massa a riposo. ma per S la massa di A NON è a riposo!
Grazie Enzo.... hai ragione... posso solo dire che l'errore è tutto mio, ossia non ho sbirciato in rete.. ho fatto tutto da solo...
posso solo dire che l'errore è tutto mio, ossia non ho sbirciato in rete.. ho fatto tutto da solo...
Gulp ripensandoci forse detta così è pure peggio
Volevo, però, far notare che è utile esporre dubbi o al contrario ciò che si pensa di aver capito, perchè così gli errori emergono prima che si cronicizzino...
Paolo
Esattamente Paolo!
i dubbi e le interpretazioni personali sono estremamente utili per una divulgazione partecipata!
So benissimo che non hai sbirciato, ma il tuo errore è quello tipico di molti professionisti o presunti tali... In realtà, sembra veramente riuscire a mettere le cose a posto senza troppa fatica. Qualcosa di molto simile all'elettrone che vede distruggersi il muro di cui avevamo parlato all'inizio della dinamica relativistica...
Non ti preoccupare, quindi, dato che è cosa abbastanza comune anche tra gli addetti ai lavori. E' comunque un errore che deriva dalla comprensione della RR. Se no, non si potrebbe nemmeno commettere. Un errore che scivola veramente tra le righe...
caro Paolo,
sono comunque convinto che riusciresti ad arrivarci da solo, sapendo come deve essere impostata la massa relativistica... Se hai tempo prova pure... i passaggi matematici non sono certo difficili. Bisogna solo ragionare con calma ed eseguire i vari passaggi con molta logica e tranquillità.
NB: stamattina, a mente fresca, ho riguardato attentamente quest'articolo e quello precedente: oltre agli errori evidenziati da Dany, mi sono accorto di altre piccole sviste (un blu che era diventato un rosso, un pedice che era scomparso...). Spero ardentemente che ora sia tutto a posto. Vi consiglio, perciò, di rileggere il testo (una volta in più non fa mai male...)
Ancora grazie a chi mi aiuta in questo lavoro di "messa a punto"....
scusa, ma ho un dubbio.Parto da un ragionamento che si riferisce all'articolo precedente (caso Galileo), in cui volevo considerare due velocità per A e B diverse. In questo caso la quantità di moto totale non si annulla. Però l'urto elastico fa sì che le componenti verticali della velocità si invertano, essendo le masse uguali. Questo fa sì che la quantità di moto totale abbia sempre lo stesso segno, e si conservi e questo è assodato. Ora che differenza c' è dal caso relativistico a livello di urto elastico? Abbiamo due masse uguali che viste da S si avvicinano con velocità Uo e Uby diverse. Perchè possiamo asserire che dopo l'urto le due velocità cambiano solo di segno e non invertono il modulo? Non conosciamo ancora l'urto relativistico. Ma senza questo non possiamo dire che la quantità di moto non si conserva. Mi sembra un cane che si morde la coda.
ho paura di non avere capito cosa intendi dire... :roll, comunque ci provo... E' solo la velocità di S' che subisce la contrazione, sia prima che dopo l'urto. Perché dovrebbero invertire il modulo? Che sia in un verso o nell'altro è solo la velocità di S' vista da S che si contrae. Se le velocità fossero diverse, come dici tu, avremmo che pur invertendo il modulo la velocità di S' vista da S si contrarrebbe anche dopo l'urto e non sarebbe comunque uguale a quella di S.
Era questo il problema?
Sono io che non riesco a spiegarmi;
L'urto lo stiamo vedendo da S? Parliamo di componenti verticali
A Ha velocità Uo; Vede B che si avvicina con velocità ridotta relativisticamente
a Uby<Uo; io parlo di queste due componenti che sono diverse, non stiamo considerando queste nell'urto e nel calcolo di q?
caro Umberto,
forse dimentichi che il fenomeno fisico deve restare uguale, se il moto è uniforme. Il che vuol dire che la pallina di S si deve comportare come quando S' non si muoveva e quindi deve rimbalzare con la stessa velocità cambiata di segno. La stessa cosa deve avvenire per quella di S' che deve tornare indietro con la stessa velocità dell'andata. Facendo i calcoli S deve dedurre che la qm verticale non si è conservata.
In realtà, puoi anche considerare che dopo l'urto si è scambiato il modulo, ma la contrazione fa sì che quel modulo appaia contratto...
cerco di spiegarmi ancora meglio (sempre che abbia capito)...
L'urto è lo stesso di quando i sistemi erano fermi. Poco importa se S vede arrivare più piano la pallina blu... lui sa che la pallina rossa deve tornare indietro con la stessa velocità dell'andata. La stessa cosa deve anche capitare alla pallina blu per ovvia simmetria. A questo punto è ovvio che pensa che qualcosa non vada per il suo verso e allora calcola le quantità di moto e vede che in realtà non si conservano. Ragione per cui deduce che la RR , ossia ciò che vede, non conserva la qm...
A me sembra del tutto logico e non qualcosa che si morde la coda... perché mai dovrebbe vedere la pallina blu tornare indietro con un'altra velocità, magari la sua? Se succedesse la simmetria si romperebbe e questo non può essere vero!
No, hai capito benissimo il mio dubbio; a parte i semplici calcoli non avevo capito questo dell'articolo, e mi è sembrato doveroso chiarirlo. Non pensavo allo stesso fenomeno visto da due rifermenti inerziali diversi. Però mi sembra importante averlo evidenziato.
hai ragione... lo davo per assodato considerando la RR. Tuttavia, adesso ti è chiaro il discorso? L'importante è eliminare qualsiasi dubbio... e hai fatto benissimo a sollevarlo. Questo è il metodo migliore per permettermi di migliorare la divulgazione
a questo riguardo andava benissimo l'esempio che ho indicato, all'inizio, come confusionario, in quanto parlava solo di velocità di trascinamento dei sistemi. Mi riferisco all'elettrone che vede una certa massa cadere contro un muro. Lui vede veramente crollare il muro anche se la massa sembra andare al rallentatore, dato che il fenomeno non può cambiare. Non può che rimanere allibito e stralunato... e, visto che è intelligente, pensare che nella RR la quantità di moto non può conservarsi!
Volevo dirtelo prima; mi piaceva di più l'esempio dell'elettrone, era più intuitivo e lo avevo capito meglio.Qui ho fatto un pò fatica.
Il fatto è che quello dell'elettrone cerca di far quadrare la quantità di moto e non la sua conservazione. Il concetto è sbagliato... La differenza non è piccola cosa, ma molto importante. Altrimenti perché fare esempi più complessi? Con le due palline si può realmente quantificare la qm e vedere se si conserva oppure no... In quel caso, invece, si diceva che se il muro si rompeva comunque e la quantità di moto era quella che era, allora doveva cambiare la massa pur di mantenerla uguale, avendo velocità inferiore. pensaci bene... non è la stessa cosa!
Penso che tu abbia i tuoi fondati motivi per aver introdotto questo esempio.
Io non posso che attendere la prossima svolta, a posteriori capirò meglio.
Il succo di tutto è questo:
io guardo un fenomeno che dà luogo a un rimbalzo in cui la velocità dell'andata è uguale alla velocità del ritorno (urto elastico frontale con pari massa e velocità). Punto. Noto anche che la qm si conserva.
Faccio muovere S' e il fenomeno non deve cambiare. Le velocità di andata devono essere uguali a quelle di ritorno, ma posso anche calcolare le velocità e verificare la quantità di moto totale prima e dopo, in senso verticale. La qm non si conserva e quindi devo cambiare la sua definizione. Punto.