Il problema da risolvere è  partire con la conservazione della quantità di moto, la conservazione della massa relativistica e il principio di relatività e trovare la formula che lega massa relativistica e massa a riposo, utilizzando un urto completamente anelastico (QUI).

Eravamo arrivati a scrivere:

m₀/m = v/u - 1

In altre parole, la relazione tra le masse si poteva tranquillamente trovare attraverso il rapporto tra le velocità, in particolare quella con cui la massa in movimento si dirige verso l’altra massa ferma (v) e quella della massa finale dopo l’urto (u).

Lasciamo da parte le masse e dedichiamoci solo a trovare il rapporto tra le velocità.

Immaginiamo di porci in un sistema di riferimento diverso e descrivere nuovamente il fenomeno che deve rimanere sempre lo stesso per il principio di relatività. Scegliamo il sistema S’ che si muove esattamente con la velocità del corpo rosso. In altre parole, la velocità di trascinamento di S’ rispetto a S sia proprio v.

Otteniamo la nuova Fig. 2, in cui la palla rossa risulta ferma, mentre è la blu che si muove con velocità - v.

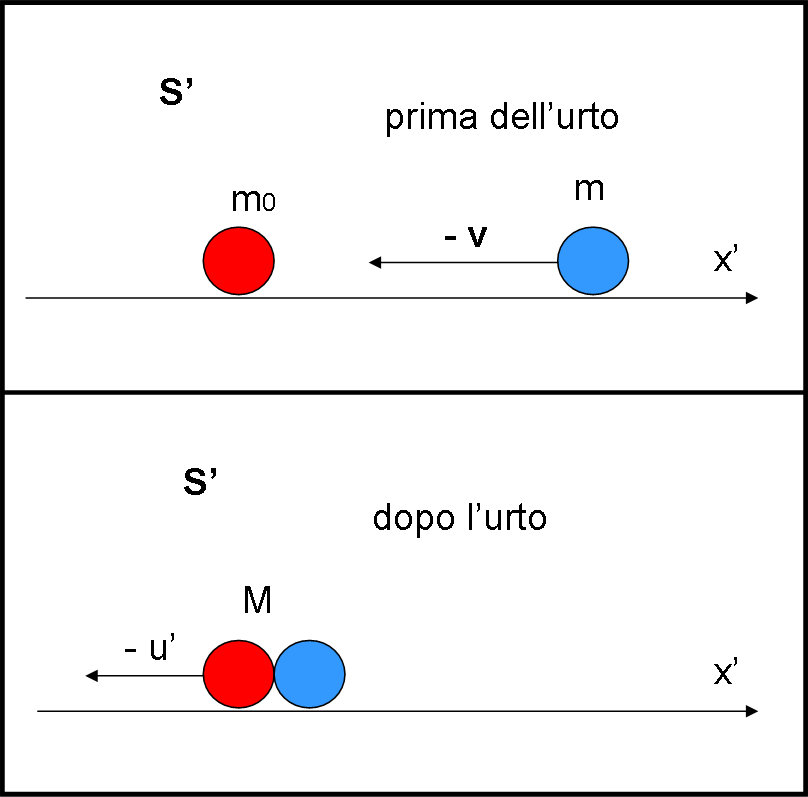
Applichiamo la conservazione della quantità di moto e abbiamo:

- mv  = - (m + m₀)u’

Tutto è rimasto identico, tranne che il verso delle velocità. Ne segue che:

u = - u’

Tuttavia, possiamo anche scrivere u’ sfruttando la composizione delle velocità (il sistema S si muove con velocità - v rispetto a S’), ossia:

u’ = (u - v)/(1 - uv/c²)

ma

u’ = - u

e, quindi, otteniamo la relazione:

- u = (u – v)/(1 – uv/c²)

Sviluppandola, troviamo una semplice equazione di secondo grado in u, che ci permette di ricavare la relazione tra u e v.

- u + u²v/c² = u - v

(v/c²)u² - 2u + v = 0

Le due soluzioni si trovano immediatamente ricordando questo articolo:

u = (1 +/- (1 - v²/c²)^1/2)/(v/c²) = (c²/v) (1 +/- (1 - v²/c²)^1/2)

Quale soluzione scegliere? Beh… sicuramente non la prima, ossia:

u₁ = (c²/v) (1 + (1 - v²/c²)^1/2)

dato che essa risulta maggiore della velocità della luce. Infatti:

(1 – v²/c²)^1/2 > 0

(1 + (1 - v²/c²)^1/2) > 1

c/v > 1

c²/v = c c/v > c

Moltiplicando un numero maggiore di uno per qualcosa maggiore di c otteniamo qualcosa maggiore di c.

Non posiamo che accettare la seconda soluzione, ossia:

u = u₂ = (c²/v) (1 - (1 - v²/c²)^1/2)

Adesso, con molta calma, eseguiamo un po’ di “noiosi” passaggi matematici

v/u = v /((c²/v) (1 - (1 - v²/c²)^1/2)) = (v²/c²)/(1 - (1 - v²/c²)^1/2)

Moltiplichiamo sopra e sotto per una stessa quantità (1 + (1 - v²/c²)^1/2) e abbiamo:

v/u = (v²/c²) (1 + (1 - v²/c²)^1/2)/((1 - (1 - v²/c²)^1/2) (1 + (1 - v²/c²)^1/2))

Ma siamo matti? No… basta ricordarsi i prodotti notevoli (QUI) e, in particolare, la relazione (7):

(a - b)(a + b) = a² - b²

Il denominatore è proprio qualcosa del genere e possiamo scrivere:

v/u = (v²/c²) (1 + (1 - v²/c²)^1/2)/(1 - (1 - v²/c²)) = (v²/c²) (1 + (1 - v²/c²)^1/2)/(v²/c²)

semplificando:

v/u = 1 + (1 - v²/c²)^1/2

Ma a noi interessa la quantità (v/u - 1) che è proprio m₀/m. Basta scriverla…

m₀/m = v/u - 1 = 1 + (1 - v²/c²)^1/2 - 1 = (1 - v²/c²)^1/2

E, infine:

m = m₀/(1 - v²/c²)^1/2

C.V.D.

Ovviamente un BRAVO a tutti coloro che hanno risposto esattamente, pur cambiando un po’ i passaggi matematici (cosa più che normale).