Categorie: Relatività
Tags: accelerazione forza Newton quantità di moto seconda legge dinamica velocità
Scritto da: Vincenzo Zappalà
Commenti:13
Dinamica relativistica. 2: la velocità deve avere dei limiti. 1 **
Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo
Nessuno vuole distruggere la dinamica classica, ma bisogna accettare che essa valga solo per velocità ridotte, simili a quelle con cui siamo abituati a convivere e che sono, comunque, ancora compatibili con quelle necessarie a trasportare con grande precisione le sonde spaziali in giro per il Sistema Solare. Einstein non distrugge, ma migliora pur rivoluzionando i concetti di base. Sembra ancora impossibile che, scardinando completamente la struttura generale della realtà, sia riuscito a preservare il contributo della fisica precedente. Già questo risultato meriterebbe dieci Nobel…
Abbiamo posticipato la dinamica relativistica per dare spazio alle nozioni fondamentali di sviluppo in serie e di integrale definito e indefinito. Il motivo era proprio quello di poterli utilizzare ed eseguire i vari passaggi nel modo più corretto e rigoroso. Ne segue che chi non li ha ancora “digeriti” potrebbe avere una qualche difficoltà. Posso consigliarvi di andare a leggere i relativi capitoli sugli integrali (veramente banali) negli approfondimenti di matematica? Vi assicuro che la loro comprensione concettuale è veramente di scarsa difficoltà. E poi, in fondo, basta sapere che l’integrale è l’operazione inversa della derivata o -se preferite- che rappresenta la somma di tanti intervallini infinitesimi.
Tuttavia, sapete che, in fondo, sono un “buono” e, di conseguenza, ogni volta che sarà possibile, accosterò alla trattazione più rigorosa e generale, anche una qualche scorciatoia (o allungatoia…) che la eviti. Non sentitevi, comunque, autorizzati a lasciare gli integrali nel dimenticatoio, mi raccomando…
Consideriamo subito la legge forse più importante del moto dei corpi, la seconda, quella che dice che una forza è data dalla variazione della quantità di moto rispetto al tempo. Non stupitevi… per Newton è del tutto equivalente alla scrittura più famosa:
F = ma
Infatti:
F = ma = m dv/dt = d(mv)/dt = dq/dt
Attenzione: abbiamo fatto un passaggio che andava bene per Newton, ma non per noi… Abbiamo, infatti, considerato la massa costante inserendola nella derivata.
Noi preferiamo utilizzare, perciò, la relazione:
F = dq/dt
e vedere cosa succede nel caso in cui la quantità di moto sia relativistica. La relazione precedente vale, infatti, nel caso generale, senza imporre niente sulla costanza della massa.
Ammettiamo che un corpo sia soggetto a una forza costante e che sia inizialmente fermo. In poche parole, al tempo t = 0 vale v = 0. Lasciamo che la forza agisca per un certo tempo t. In parole povere, possiamo tranquillamente evitare la scrittura vettoriale e lavorare con i moduli, dato che tutto si muove o fa muovere nella stessa direzione.
Abbiamo una derivata di mezzo e salta subito all’occhio che il modo migliore per far comparire la quantità di moto è quello di integrare entrambi i membri della relazione precedente nell’intervallo di tempo t. In altre parole, sommiamo tutti contributi infinitesimi della variazione della quantità di moto per un certo intervallo di tempo t.
∫0t F dt = ∫0t (dq/dt) dt
Tuttavia, la forza F è una costante e quindi:
∫0t F dt = F ∫0t dt = F (t - 0) = F t
Ricordiamo che l’integrale indefinito di 1·dt non è altro che t
Il secondo membro vede al suo interno proprio una derivata (quella della quantità di moto) e quindi:
∫0t (dq/dt) dt = q(t) – q(0)
Ne segue:
F t = q(t) – q(0)
E, ancora:
F t = q(t) …. (1)
dato che per t = 0 abbiamo v = 0 e, quindi, anche q(0) = 0.
Chi ha un po’ di dimestichezza con la fisica classica, ha già riconosciuto la grandezza che abbiamo appena trovato: il prodotto della forza per il tempo in cui viene applicata. Essa viene chiamato impulso di una forza (un giorno ne parleremo più a lungo, lo prometto). La relazione precedente enuncia una legge della meccanica classica ben conosciuta che dice: l’impulso di una forza è uguale alla variazione della quantità di moto (nel nostro caso, il secondo membro è una variazione dato che q(0) = 0).
Il fatto che l’abbiamo ricavata, senza imporre alcuna costrizione alla quantità di moto, ci assicura che questa legge rimane valida anche nella dinamica relativistica. Sembrerebbe una sottigliezza, ma, invece, è un punto molto importante, dato che la sua validità ci mostrerà tra breve come è costretta a variare la velocità.
Prima di proseguire, volevo tirare un po’ su di morale chi non ha ancora digerito gli integrali.
La relazione:
F = dq/dt
poteva essere scritta:
dt F = dq
o, anche:
∆t F = ∆q
Ossia:
(t – 0) F = q(t) – q(0) = q(t)
Esattamente la (1). Ma allora perché tanta fatica con gli integrali? Beh, nel nostro caso, siamo di fronte a una forza costante e quindi il suo impulso vale anche per intervalli di tempo non infinitesimi. In pratica possiamo sostituire un dt con un ∆t.
La (1) rimane, comunque, un caso particolare di una definizione ben più generale che contempli anche una forza variabile. In tal caso, gli intervalli infinitesimi dt non potrebbero essere sostituiti con intervalli di ampiezza qualsiasi e l’integrale risulterebbe obbligatorio (ricordiamoci che è pur sempre la somma di tante quantità infinitesime).
Stiamo discutendo di dinamica relativistica, lo ammetto, ma le sfumature nella trattazione delle leggi fisiche devono ormai essere tenute in conto. Gli integrali, così come le derivate, devono essere valutati per quello che in realtà significano. Considerare dy/dx = ∆y/∆x può anche essere accettato, in certi casi, ma dobbiamo tenere ben presente il loro diverso significato matematico (e non solo). Una derivata è uguale a un rapporto tra intervalli finiti solo per particolari condizioni.
Per valutare ben la differenza basta andare a rileggere gli articoli che introducevano gli integrali come aree e come somma di tante aree infinitesime. Essi diventano fondamentali quando la funzione non è più una semplice retta, ma varia continuamente la sua pendenza (QUI e QUI)
Va bene, fatti tutti contenti, possiamo tornare alla (1) e chiederci: “Cosa succede alla velocità di un corpo di massa m0 a riposo, su cui agisce una forza costante, se si sostituisce alla definizione di quantità di moto classica quella relativistica?”. Bene, cominciamo col ricordare il primo caso.
a) Quantità di moto classica
La quantità di moto classica è data da:
q = m0v(t)
La (1) diventa:
F t = m0v(t)
E ancora:
v(t) = (F/m0)t …. (2)
Il rapporto F/m0 è una costante (e sappiamo che prende il nome di accelerazione…), da cui segue che la velocità è una funzione lineare del tempo, ossia descrive una retta che ha proprio l’accelerazione (costante) come coefficiente angolare.
La possiamo disegnare tratteggiata nella Fig. 1, dove alcuni valori "critici" saranno introdotti la prossima volta.
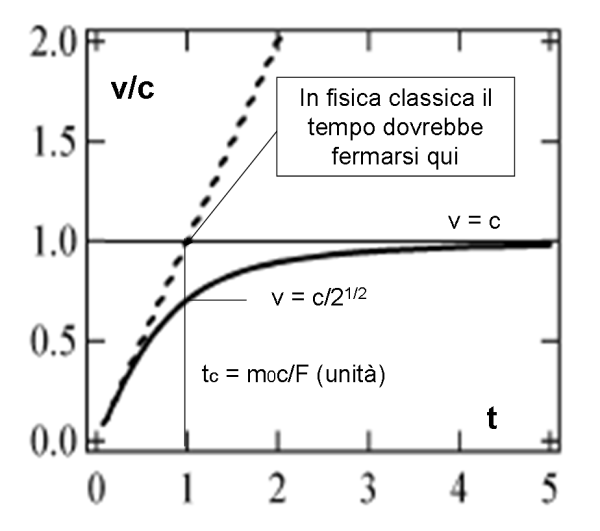
Questo è quanto ci dice la seconda legge di Newton… Purtroppo, il risultato non è accettabile dalla RR. Consideriamo un tempo tc tale che:
tc ≥ m0c/F
Niente può vietarci di raggiungerlo e di superarlo. Avremmo:
v(tc) ≥ (F/m0) (m0c/F) = c
In altre parole, al posto di t possiamo inserire un suo valore qualsiasi, dato che niente blocca il tempo. Consideriamo proprio tc = m0c/F che,sostituito nella (2) porta a un valore di v uguale a c. Per valori di t superiori ne consegue che la velocità supera quella della luce.
E qui le cose non vanno più bene...
Sembrerebbe quasi che la forza possa agire solo per un certo tempo, ma questo non ha alcun senso fisico o almeno non per adesso. In realtà, la forza agisce sempre, ma non comporta un valore costante dell’accelerazione. Il suo sforzo serve sempre di più a far crescere la massa… Lo vediamo subito.
b) Quantità di moto relativistica
Riprendiamo la (1), ma questa volta utilizziamo la definizione relativistica della quantità di moto, ossia:
qR = mvv(t) = m0 γ v(t)
dove, tanto per non dimenticare:
γ = 1/(1 – v2(t)/c2)1/2
Notiamo, ancora una volta, che la velocità che entra in gioco e proprio la velocità del corpo in movimento.
Sostituendo nella (1), otteniamo:
F t = qR(t) = m0γv(t) = m0v(t)/(1 - v2(t) /c2)1/2
v(t) = F (1 - v2(t) /c2)1/2 t/m0 …. (3)
Notiamo che l’incognita velocità si trova sia a sinistra che a destra. E’ necessario risolvere l’equazione (3), in modo da esplicitare la velocità in funzione del tempo. Non è certo impresa difficile… basta un po’ di matematica elementare. Ad esempio, eleviamo al quadrato entrambi i membri:
v2(t) = F2 (1- v2(t) /c2) t2 /m20
m20 v2(t) = F2 t2 - F2 v2(t) t2/c2
v2(t) (m20 + F2t2/c2) = F2 t2
v2(t) = F2 t2/(m20 + F2t2/c2)
v(t) = Ft/(m20 + F2t2/c2)1/2 …. (4)
Questa è una funzione del tempo che sappiamo sicuramente studiare. In particolare, possiamo facilmente calcolare l’asintoto orizzontale che si ottiene facendo tendere il tempo a infinito.
Il limite della v(t) diventa una forma infinito su infinito, ma sappiamo bene come risolverlo, dato che numeratore e denominatore hanno lo stesso grado (la radice quadrata di t2 ha lo stesso grado di t). Il limite si riduce al rapporto tra i due coefficienti dei termini di grado massimo:
lim t→∞ Ft/(m20 + F2t2/c) = c F/F = c
L’asintoto orizzontale è dato dalla retta v = c. In poche parole, la velocità non può superare la velocità della luce. Sì, adesso le cose vanno molto meglio, come si vede dalla curva continua della Fig. 1.
Tuttavia, la (4) merita tutta una serie di riflessioni che troppo spesso non vengono sufficientemente evidenziate.






13 commenti
cari amici,
da questo momento in poi, vi prego di seguire con molta attenzione la dinamica relativistica. Solo così, tra non molto, arriveremo quasi senza accorgercene alla
e potremmo dire: "Banale!"
Ho bisogno di un chiarimento, Enzo: non ho capito come si passa da
Grazie!
dunque...
la v è una funzione di t, come si vede dalla
v(t) = (F/m0)t
Al posto di t possiamo inserire un suo valore qualsiasi, dato che niente blocca il tempo. Consideriamo proprio tc = m0c/F e andiamo a sostituirlo nella relazione precedente:
v = (F/m0)(mo c/F) = F moc/F m0 = c
la velcoità diventa quella della luce e quindi per ogni valore di t superiore la v deve superare quella della luce.... impossibile!
Grazie anche per i suggerimenti: eseguirò qualche leggera modifica per rendere ancora tutto più chiaro... L'importante è che nessuno abbia dubbi!
per tutti...
ho aggiunto qualche dato nella figura per aiutare la comprensione del valore critico del tempo...
Prima di interessarmi di fisica mi chiedevo come facesse un razzo a trovare la spinta sul vuoto.Non riuscivo ad immaginarmi che "appiglio"avesse il gas che fuoriusciva.Le onde elettromagnetiche si propagano ma non sono materia sono uno stato dinamico di energia,ma il gas del razzo è materia e deve trovare qualcosa di elastico che gli restituisce energia...?
Caro Enzo ho provato a girare e rigirare la relazione (3) per ricavare altre relazioni... sperando di non aver commesso madornali errori.
In sintesi:
v(t) =F√(1 - v²(t)/c²) t/mo (3)
v(t) =F√(1 - v²(t)/c²) t/mo
mo/√(1 - v²(t)/c²)= F t/v(t)
ma mo/√(1 - v²(t)/c²) è la massa relativistica m(v)
m(v)= F t/v(t)
Nella fisica classica, con accelerazione costante:
F=ma..... F = m v(t)/t......... m= Ft/v(t)
Usando la massa relativistica invece di m0 le relazioni si eguagliano, o sbaglio?
Ora ricavo la Forza:
v(t) =F√(1 - v²(t)/c²) t/mo
F = (v(t)/t) mo/√(1 – v²(t)/c²)
Come prima se invece di m0 uso m(v): F = (v(t)/t) m(v)
Ricavo il tempo:
v(t) =F√(1 - v²(t)/c²) t/mo
t = v(t) mo/√(1 - v²(t)/c²) F
Come prima se invece di m0 uso m(v): t = v(t) mo/F
Ricavo l'accelerazione a = dv/dt:
v(t) =F√(1 – v²(t)/c²) t/m0…
v(t)/t =F√(1 – v²(t)/c²)/m0
a = F√(1 - v²(t)/c²) /m0…
a = F/m0…√(1 – v²(t)/c²)
ma F/m0 è l'accelerazione secondo la fisica classica (F=ma... a = F/m)
a = a (classica)…√(1 - v²(t)/c²)
a = a (classica)/γ
Qui, invece, emerge la differenza tra due diversi modi di calcolare l'accelerazione, ma non ho usato la massa relativistica, ma la massa a riposo...
Altrimenti:
v(t)/t =F√(1 – v²(t)/c²)/m0…
m0/√(1 – v²(t)/c²) =Ft/v(t)
m(v) = Ft/v(t)
v(t)/t= F/m(v)
a= F/m(v)
Sono corretti questi passaggi, oppure sto sbagliando qualcosa?
Paolo
caro Paolo,
hai girato un po' a vuoto... ma, alla fine, hai trovato che l'accelerazione dipende dalla velocità in quanto la massa dipende anch'essa dalla velocità. Concetto decisivo per la RR.
Se vuoi arrivare a qualcosa di ancora più "concreto" ti consiglio di ricavare la seconda legge della dinamica (sotto la forma F = ma) nel caso relativistico.
Volevo anche inserire questa parte nel testo, ma poi ho preferito soprassedere anche per l'interesse secondario e per la rapida caduta verso la RG.
Comunque è un bell'esercizio. Tutto sta a prendere F = dq/dt e scrivere q relativistico. A quel punto la derivata d(vm)/dt non è semplice come nel caso classico...
ho provato a fare la derivata; ma bisogna lasciare il tutto in funzione di v(t)?
caro Umberto, la derivata è rispetto al tempo... quindi l'importante è che tutto sia espresso in funzione del tempo. Comunque, non c'è bisogno di svolgere le derivate per intero, basta trovare un'immediata conseguenza della relatività ...
Vedo passare a folle velocità un pallone spinto da una siringa piena di energia.La velocità del sistema pallone siringa arriva quasi a toccare quella della luce,a quel punto il tutto rallenta,impedendo di raggiungere la velocità luminare,la palla si schiaccia nella direzione del movimento e la siringa penetra con l'ago nel pallone iniettandoci dentro sempre più energia facendolo sempre più massivo man mano che la velocità si avvicina al limite
in qualche modo corrisponde... ma è meglio prendere un palloncino molto piccolo se no lo vediamo sgonfiarsi miseramente molto prima... non conosciamo siringhe così potenti! Si scherza, ovviamente...
Si scherza, ovviamente...
per il discorso di ieri per ricavare la seconda legge della dinamico nel caso relativistico, mi è venuto in mente il quiz dove dovevamo dimostrare:
dove :
????
caro Umberto,
direi che tutto è molto più semplice (per avere una visione immediata)...
m = γ m0
e γ è una funzione del tempo.
Siamo allora obbligati a scrivere:
F = d(mv)/dt = m dv/dt + dm/dt v (derivata di un prodotto …)
Ma, sappiamo molto bene che:
dv/dt = a
e quindi:
F = m a + dm/dt v
e, infine:
a = F/m - (v/m) dm/dt
Come vedi non c'è nemmeno bisogno di esplicitare la derivata di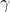 per dire che l'accelerazione ha un termine che ha la stessa direzione della velocità...
per dire che l'accelerazione ha un termine che ha la stessa direzione della velocità...
Se il corpo avesse una velocità diretta in modo diverso dalla forza, l'accelerazione finale non sarebbe, nemmeno lei, diretta come la forza. Ciò capita, ad esempio, quando una particella viene lanciata attraverso un campo che le impone una forza. L'accelerazione della forza subisce una variazione dovuta alla velocità della particella. Tuttavia, preferisco non entrare nei dettagli anche perché per ottenere risvolti importanti si sconfina rapidamente nella RG.
Accontentiamoci di dire che l'accelerazione è comunque variabile a parità di forza, dato che risente di un'inerzia crescente con la velocità... Insomma, F/m non è più una costante... e questa è una vera rivoluzione concettuale!