Per una trattazione completa dell’argomento affrontato in questo articolo, si consiglia di leggere il relativo approfondimento

Conosciamo tutti le tre leggi di Keplero. E se non fosse vero, le richiameremo, comunque, tra non molto. Tuttavia, sappiamo che esse sono state ricavate attraverso le osservazioni dirette, senza preoccuparsi di quale fosse la legge fisica che le originava.

D’altra parte, però, sappiamo anche che la legge di gravitazione universale descritta da Newton ha come ricaduta proprio il moto di un corpo attorno a un altro (o -se preferite- attorno al comune baricentro).

E’, quindi, più che ovvio che uno sia convinto che le leggi di Keplero debbano poter essere ricavate dalla legge di Newton. A prima vista, sembrerebbe una derivazione semplice e, invece, non lo è affatto! Ad esempio, assumendo un moto circolare uniforme, è possibile ricavare quasi immediatamente la terza legge di Keplero, ma ben diversa è la situazione, se ammettiamo orbite ellittiche.

Abbiamo ormai le conoscenze, sia matematiche che fisiche, sufficienti per affrontare analiticamente il moto di due corpi. Ricordiamoci che, se già passassimo ai tre corpi, non avremmo più una soluzione analitica (se non per casi molto particolari). Il problema di due corpi è quindi tutt’altro che una semplice ovvietà.

Conosciamo anche gli integrali e quindi non dovremmo avere alcun intoppo. In realtà, la faccenda è un po’ più complicata, nel senso che per riuscire a svolgere completamente il nostro esercizio è necessario introdurre un’equazione differenziale e risolverla.

Senza spaventarsi troppo, questo vuole anche dire calcolare integrali ben più complessi di quanto visto nei capitoli a loro dedicati nella matematica. Continuare nel calcolo integrale, per riuscire a risolvere quello di cui avremmo bisogno, sarebbe, però, una fatica enorme e necessiterebbe di nozioni sui numeri complessi e altro ancora. Non penso sia il caso di spingersi così avanti con la matematica. Ho deciso, perciò, di accettare come dato di fatto la soluzione di un integrale non certo banale. E’ solo un passaggio, perché tutto il resto è alla nostra portata, ve lo assicuro!

In ogni modo, per i più esperti e/o volenterosi, cercherò un sito dove sia descritta completamente la descrizione della soluzione.

Comunque, per adesso, non pensiamoci, e cominciamo ad affrontare il problema che ci deve portare da Newton a Keplero.

Per fare ciò è necessario richiamare due concetti, uno già conosciuto e uno del tutto nuovo, ma che si collega facilmente a quanto abbiamo appena discusso sul moto uniformemente accelerato. Il primo è l’utilizzo delle coordinate polari, estremamente più utili per il nostro scopo; il secondo è la definizione di un’equazione differenziale (non la sua soluzione…) e una sua immediata applicazione al moto con accelerazione costante.

Iniziamo, quindi, con questi due preliminari, limitati a quanto ci sarà veramente utile.

Vorrei aggiungere che non è facile trovare questa trattazione a livello divulgativo, anche se sembrerebbe di un’importanza enorme. Noi cercheremo di fare delle piccole approssimazioni, del tutto trascurabili, che ci aiuteranno a tenerci sempre su un livello comprensibile a tutti coloro che hanno seguito le lezioni di matematica e un po’ di fisica classica, a livello velocità, accelerazione e momento angolare o poco più.

Coordinate polari: un richiamo e qualche esercizio

Anche se le abbiamo usate spesso, non sono mai state introdotte in modo specifico. Lo facciamo adesso, anche se risultano del tutto ovvie, conoscendo le funzioni trigonometriche più semplici (QUI).

Consideriamo un punto P in un sistema di assi cartesiani. Esso viene individuato dalle due coordinate x e y, come rappresentato in Fig. 1.

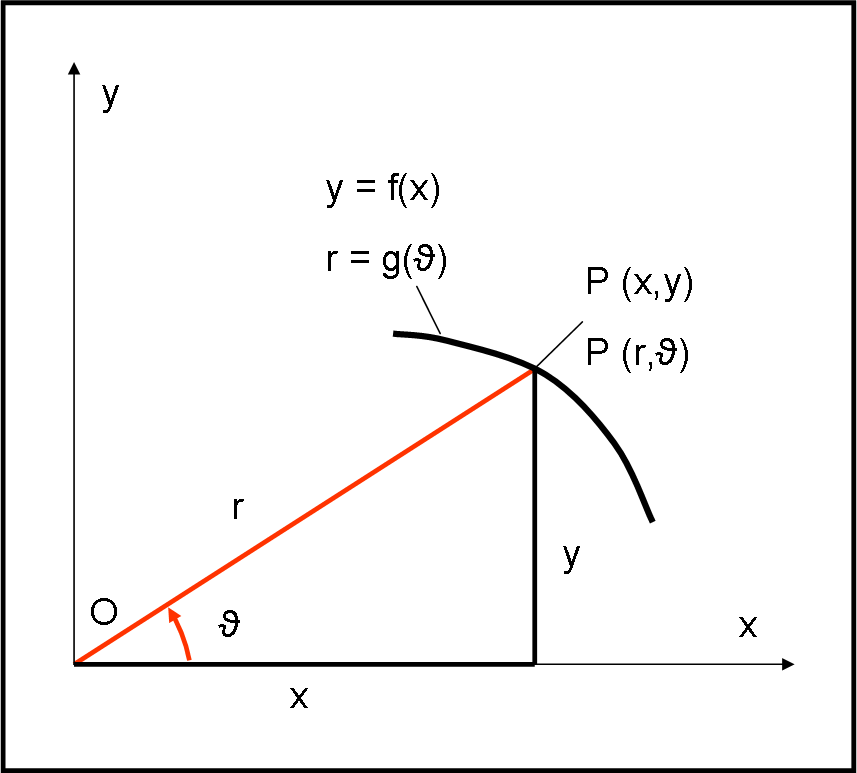
Lo stesso punto, però, può anche essere individuato con altre due coordinate: la distanza dall’origine r e l’angolo ϑ tra asse x e segmento r. Il passaggio da un sistema all’altro è banale, ricordando le funzioni trigonometriche di base.

x = r cos ϑ

y = r sin ϑ

Ne deriva che una funzione in coordinate cartesiane y = f(x) diventa in coordinate polari r = g(ϑ).

Facciamo qualche semplice esempio.

Consideriamo la retta passante per l’origine:

y = mx

In coordinate polari diventa semplicemente:

ϑ = c                      (c costante)

Ovviamente l’angolo costante c non è altro che l’angolo la cui tangente vale m (coefficiente angolare)

La circonferenza con centro nell’origine e raggio R, in coordinate cartesiane, è:

x² + y² = R

In coordinate polari non è altro che:

r = R

Infatti, per qualsiasi valore di ϑ, la distanza r rimane sempre la stessa ed è uguale al raggio.

Consideriamo una generica retta non passante per l’origine (y = mx + n). Utilizziamo la Fig. 2.

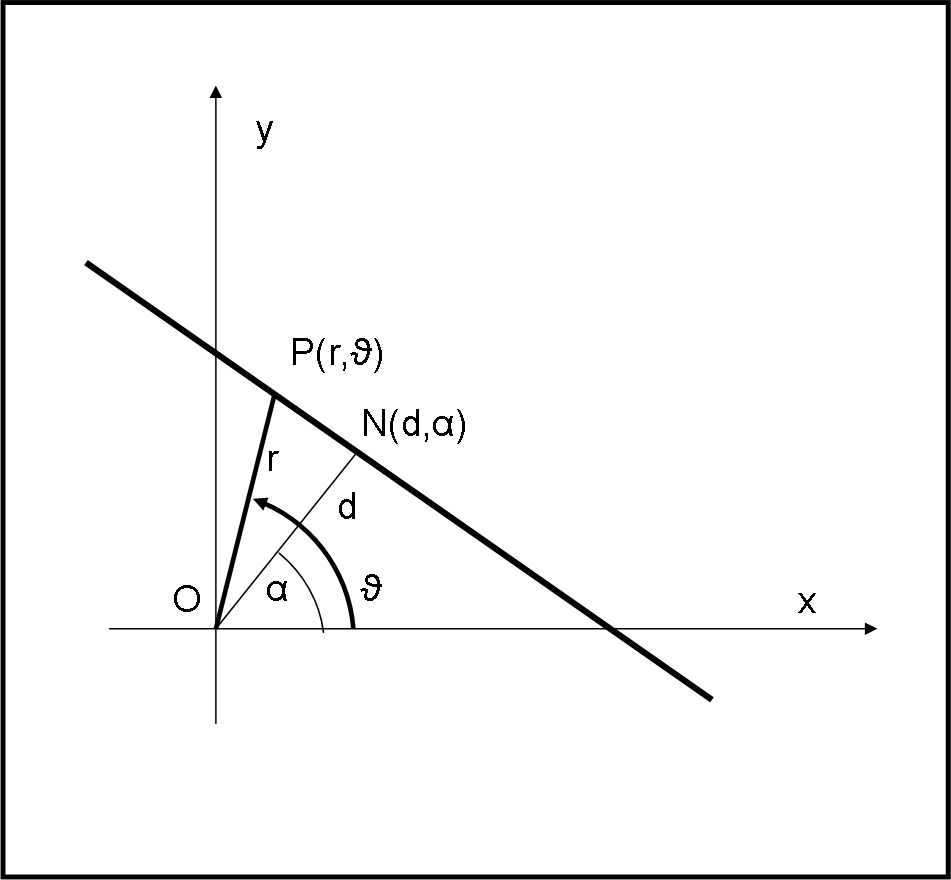
Tracciamo dall’origine la perpendicolare alla retta e sia N il punto d’intersezione. Le coordinate polari di N sono d e α. Consideriamo un punto P qualsiasi della retta che ha coordinate r e ϑ. Dal triangolo rettangolo ONP si ha subito:

d = r cos (ϑ – α)

e, quindi:

r = d/cos (ϑ – α)        dove d e α sono, ovviamente, costanti.

Insomma, è facile capire che in alcuni casi è più semplice usare le coordinate cartesiane e in altri le coordinate polari.

A noi interessa scrivere l’equazione di un ellisse considerando come origine uno dei fuochi. In questo caso sono decisamente più utili le coordinate polari, anche se dobbiamo fare qualche “noioso” passaggio per determinarle. Poi, però, tutto sarà più semplice.

Coordinate polari: l’equazione dell’ellisse

Partiamo dall’equazione in coordinate cartesiane riferite al centro dell’ellisse (Fig. 3):

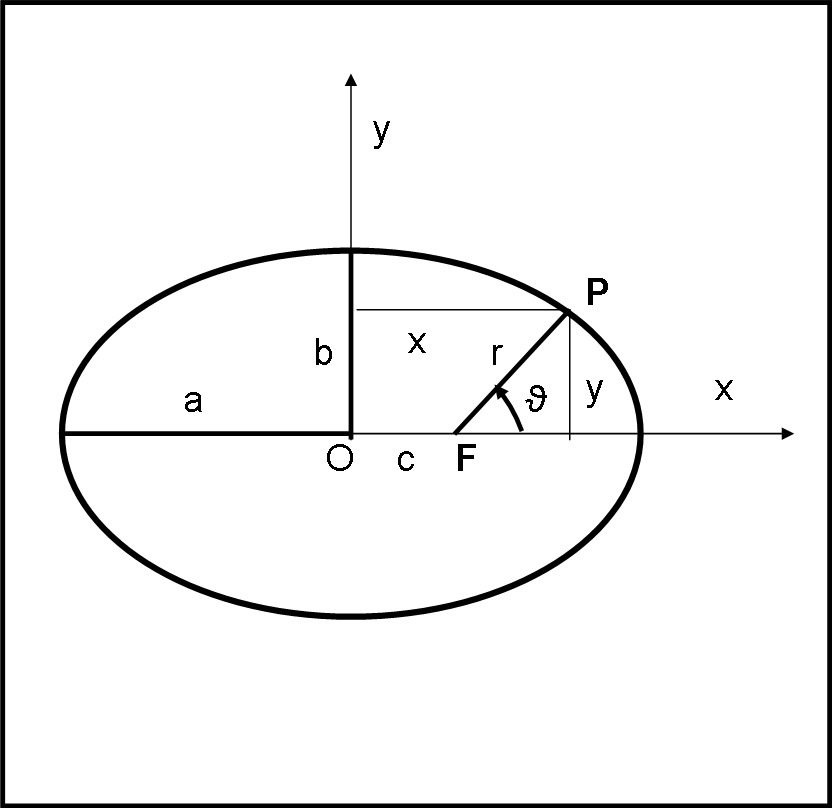
x²/a² + y²/b² = 1        …. (1)

Per questa formula e per la definizione di altri parametri potete andare QUI.

Spostando l’origine delle coordinate polari nel fuoco F, si ha:

x = c + r cos(ϑ)

y = r sin(ϑ)

Per cui, la (1) diventa:

(c² + r² cos²(ϑ) + 2rc cos(ϑ))/a² + r²sin²(ϑ)/b² = 1

b²c² + b²r²cos²(ϑ) + 2rcb²cos(ϑ) + a²r²sin²(ϑ) = a²b²

sappiamo, però, che sin²(ϑ) = 1 - cos²(ϑ), dato che:

sin²(ϑ) + cos²(ϑ) = 1

e, quindi:

b²c² + b²r²cos²(ϑ) + 2rcb²cos(ϑ) + a²r² - a²r²cos²(ϑ) = a²b²

Scriviamo c e b in funzione dell’eccentricità “e” e del semiasse maggiore a:

b = a(1 - e²)^1/2

c = ae

(1- e²)a⁴e² + a²(1- e²) r²cos²(ϑ) + 2rea³(1- e²) cos(ϑ) + a²r² - a²r²cos²(ϑ) = a⁴(1-e²)

dividiamo per a²

(1- e²)a²e² + (1- e²)r²cos²(ϑ) + 2rae(1- e²)cos(ϑ) + r² - r²cos²(ϑ) = a²(1- e²)

a²e² - a²e⁴ + r²cos²(ϑ) - e²r²cos²(ϑ) + 2raecos(ϑ) - 2rae³cos(ϑ) + r² - r²cos²(ϑ) = a² – a²e²

semplifichiamo i termini uguali e di segno opposto e raccogliamo quelli uguali:

2a²e² - a²e⁴ - e² r²cos²(ϑ) + 2raecos(ϑ) - 2rae³cos(ϑ) + r² - a² = 0

Cambiamo di segno e spostiamo qualche termine:

- 2a²e² + a²e⁴ + a² + e²r²cos²(ϑ)  - 2raecos(ϑ) + 2rae³cos(ϑ) = r²

Lavoriamo sui primi tre termini, mettendo in evidenza a²

a²(- 2e² + e⁴ +1) + e²r²cos²(ϑ)  - 2raecos(ϑ) + 2rae³cos(ϑ) = r²

a² moltiplica un trinomio che non è altro che il quadrato di (1 - e²)

a²(1 - e²)² + e²r²cos²(ϑ)  - 2raecos(ϑ) + 2rae³cos(ϑ) = r²

Mettiamo in evidenza 2raecos(ϑ) negli ultimi due termini del primo membro:

a²(1 - e²)² + e²r²cos²(ϑ) - 2rae(1 - e²)cos(ϑ) = r²

 Attenzione al primo membro! Non è altro che un quadrato.

Sostituendo, abbiamo:

(ercos(ϑ) - a(1-e²))² = r²

r = +/- (ercos(ϑ) - a(1-e²))          …. (2)

Quale segno dobbiamo prendere?

Sappiamo che r deve essere positivo. Consideriamo il caso particolare in cui e = 0. La (2) diventa:

r = +/- (-a)

a è, ovviamente, una quantità positiva, per cui, per ottenere una r positiva, dobbiamo prendere il segno meno. E questo deve valere anche nel caso generale, perciò:

r = - (ercos(ϑ) - a(1-e²))

r =  a(1- e²) - ercos(ϑ)

r(1 + ecos(ϑ)) = a(1- e²)

r = a(1- e²)/(1 + e cos(ϑ))    …. (3)

La (3) descrive un’ellisse in coordinate polari, riferita a un fuoco, al variare dell’angolo ϑ.

Il che vuole anche dire che un pianeta che orbita attorno al Sole deve descrivere l’ellisse (3), in cui a è il semiasse orbitale, “e” l’eccentricità, r la distanza del pianeta dal Sole e ϑ l’anomalia vera.

Questa non è altro che la prima legge di Keplero e quindi si dovrà arrivare a questo risultato partendo dalla legge di Newton.

Equazioni differenziali

Si fa in fretta a definire cos’è un’equazione differenziale: un’equazione che contiene le derivate di una variabile.

Qualcosa del tipo:

k d²y/dx² + h dy/dx + m y = n

L’equazione precedente descrive un’equazione differenziale del secondo ordine, lineare a coefficienti costanti. Ovviamente, si possono avere equazioni molto più complicate. Quella che abbiamo considerato, però, ci introduce al nostro problema di fondo.

Immaginiamo che y sia la posizione s di un punto e x sia il tempo t. L’equazione diventa:

k d²s/dt² + h ds/dt + m s = n

In questo caso, sappiamo molto bene cosa rappresentano le derivate: quella seconda è l’accelerazione e la prima è la velocità. Essa è un’equazione differenziale che descrive il moto di un oggetto. La soluzione, che necessita di integrali dovendo passare dalle derivate alla s, in funzione di t, descrive la legge oraria.

Facciamo due casi ancora più semplici per meglio inquadrare il concetto:

Poniamo che a (accelerazione) sia costante, si ha subito una prima equazione differenziale:

a  = dv/dt

dv = adt

Integrando ambo i membri, il primo tra v₀ e v e il secondo tra t₀ e t, si ha (vedi QUI):

∫_v0^v(dv) = ∫_t0^t (adt) = a ∫_t0^t dt

v  - v₀ = at - at₀

Ponendo t₀ = 0 si ha:

v  = v₀ + at

Che esprime la legge oraria della velocità in un moto uniformemente accelerato

La seconda equazione differenziale che prendiamo in considerazione è la seguente:

v = ds/dt

da cui:

ds = vdt

Ma conosciamo già il valore di v, dato da:

v = v₀ + at

Sostituiamo e otteniamo:

ds = (v₀ + at)dt

Possiamo integrare entrambi i membri

∫_s0^s(ds) = v₀∫_t0^t dt + a ∫_t0^t t dt

s – s₀ = v₀(t – t₀) + ½ a (t²-t₀²)

Ponendo t₀ = 0, si ha, infine:

s = s₀ + v₀t + ½ at²

che è la ben nota legge oraria del moto uniformemente accelerato.

Come già detto, però, le equazioni differenziali del moto possono essere ben più complicate e la prima legge di Keplero è proprio uno di quei casi… Noi, comunque cercheremo di arrivarci il più vicino possibile.