Per una trattazione completa dell’argomento, si consiglia di leggere il relativo approfondimento nel quale è stato inserito anche il presente articolo

Normalmente, per definire la geometria che regola una superficie sferica, si usa mischiare visione intrinseca ed estrinseca. Noi, invece, proviamo a usare le due visioni in modo separato, cercando così di entrare più a fondo nei concetti fondamentali e prepararci a quando non sarà più possibile “salire” di una dimensione. Le uniche cose che prendiamo in prestito dalle tre dimensioni sono le figure della superficie sferica. Esse, però, sono descritte da un abitante di questo strano mondo a due dimensioni. In altre parole, non sappiamo assolutamente quello che vi è all’interno della superficie sferica.

Immaginiamo, allora, di vivere su una superficie sferica (spazio curvo a due dimensioni) e di cercare di comprenderne i segreti. Questo modo di procedere lo chiamiamo intrinseco, dato che possiamo vederlo e descriverlo solo dall’interno. Ovviamente, anche noi dovremmo avere solo due dimensioni, ma ogni tanto ci permetteremo qualche piccola licenza, per spiegare meglio la situazione. Ammettiamo, anche, che i nostri geometri bidimensionali conoscano abbastanza bene la geometria del piano euclideo.

Per prima cosa vogliamo muoverci in linea retta, Come possiamo essere sicuri di farlo?

Riprendiamo una delle tante definizione di retta del mondo piano a due dimensioni: “una linea che non cambia mai direzione”.

Per vederlo in modo immediato e pratico consideriamo la Fig. 1, dove utilizziamo un carrello a due ruote.

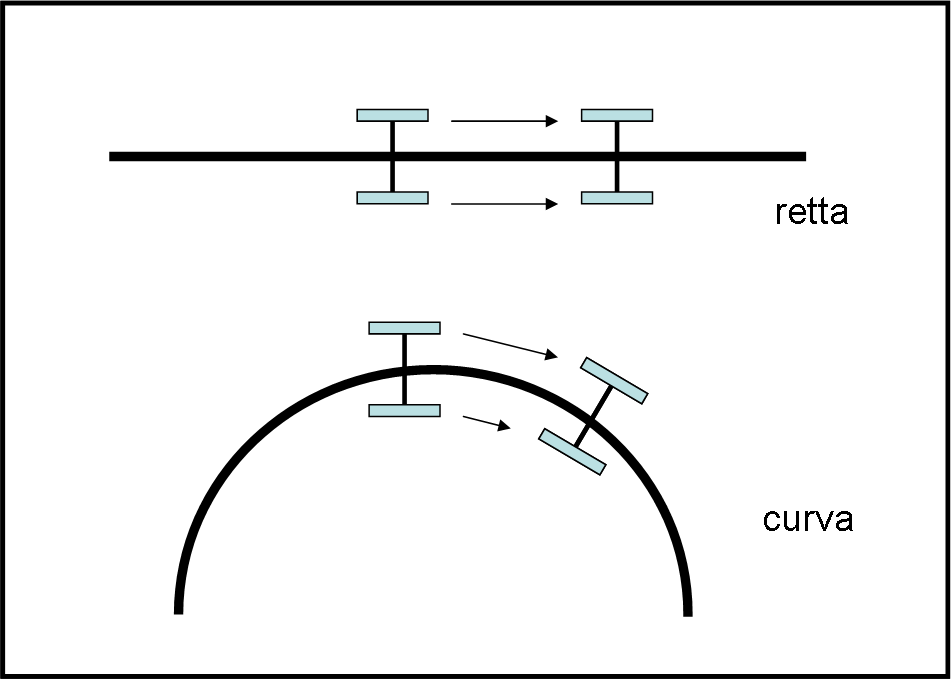
Cominciamo con il provarlo su un piano (spazio a due dimensioni euclideo). Le ruote, per la loro forma, dovrebbero già introdurre una dimensione in più, ma noi immaginiamo che siano piccolissime, praticamente piatte o microscopiche…

Come facciamo a riconoscere se il carrello va dritto o curva? Basta vedere lo spazio percorso dalle due ruote. Se la traiettoria è rettilinea le due ruoto descrivono lo stesso percorso. Se, invece, la linea è curva (ossia cambia direzione in modo più o meno costante) una delle due ruote è costretta a compiere un tragitto maggiore dell’altra.

Prendiamo adesso due punti A e B su una retta. La distanza minima è il segmento rettilineo AB. Qualsiasi altra linea che congiunga A e B è sicuramente più lunga. Insomma, per seguire il percorso minimo dobbiamo muoverci su una retta. Una linea di questo tipo viene chiamata geodetica, ossia la traiettoria più corta che unisce due punti.

Possiamo stabilire una facile regola per dimostrarlo, disegnando la Fig. 2, dove come linee curve abbiamo solo utilizzato circonferenze (ma le cose non cambierebbero usando qualsiasi altra curva).

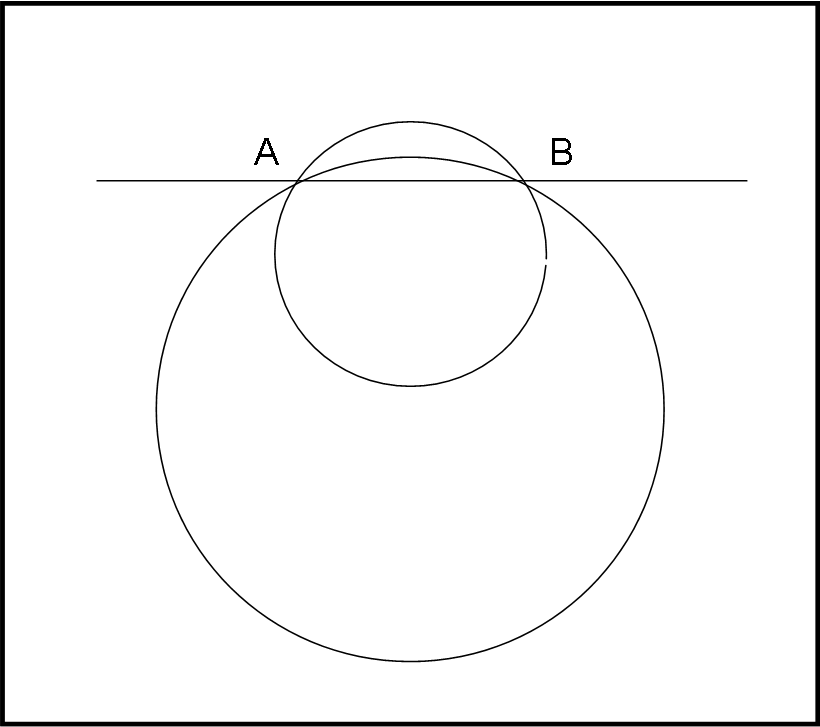
Notiamo che più la circonferenza che passa per A e B rimpicciolisce (raggio minore), maggiore diventa la distanza da percorrere per andare da A e B. In altre parole, una distanza maggiore è legata a un raggio minore. Definiamo curvatura di una circonferenza l’inverso del suo raggio, ossia 1/r. Bene, risulta ovvio che la distanza minima corrisponde alla circonferenza che ha il raggio più grande. Sul piano il raggio può essere anche INFINITO. In tal caso la curvatura 1/r è uguale a zero e cadiamo nel caso della retta. Posiamo, perciò concludere che la distanza minima si misura lungo la circonferenza che ha la curvatura minore, ossia lungo una retta.

Portiamoci adesso su una superficie sferica, senza possibilità di vederla dal di fuori. Esistono delle rette su di lei? Beh… se definiamo una retta un qualcosa che non cambia mai direzione potremmo tranquillamente utilizzare il solito carrello a due ruote, stando attenti a come girano. Mostriamo ciò che otteniamo in Fig. 3.

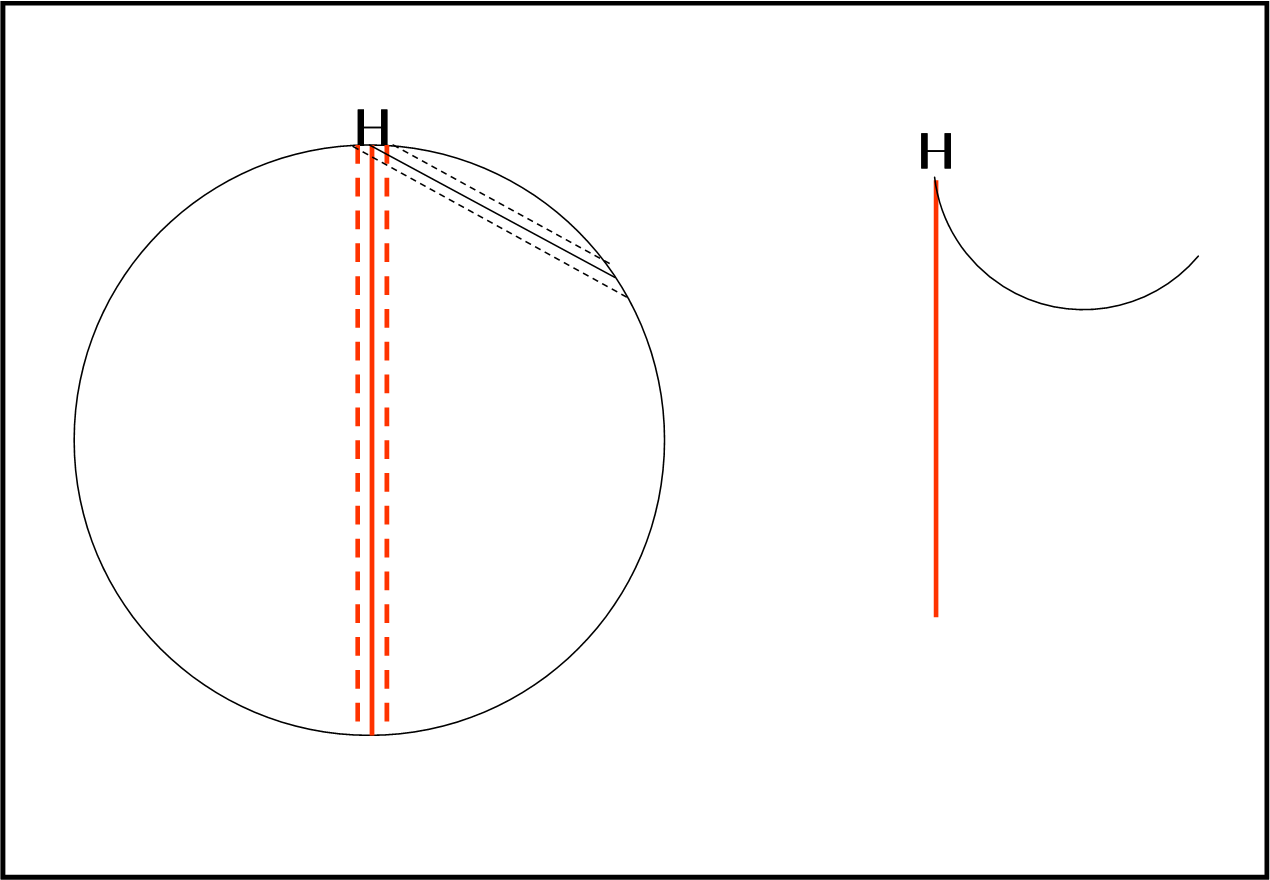
A sinistra vediamo la situazione dal di fuori. Risulta chiaro che se il carrello percorre la linea verticale esso si muove in linea retta, mentre se descrive la linea verso destra le ruote compiono percorsi diversi, quindi, il carrello descrive una curva. La visione intrinseca è quella della parte destra della figura. In altre parole, questa parte è quella che riusciamo a descrivere vivendo sulla superficie sferica. Possiamo concludere che esiste una retta e che esiste una curva. Queste due linee sono intrinseche, ossia dedotte da chi abita nelle due dimensioni. Chiamiamole retta e circonferenza intrinseche.

La faccenda funziona perfettamente, tranne un piccolo problema: pur non piegando mai, percorrendo la retta, ci ritroviamo al punto di partenza! Potremmo anche non accorgercene, ma se abbiamo usato una bandierina o qualche altro segnale, possiamo effettivamente rendercene conto. In fondo, però, ci interessa poco se nel nostro spazio a due dimensioni le rette sono traiettorie chiuse. Come nel piano, possiamo partire da qualsiasi punto della superficie e vi è sempre un retta che passa per quel punto. Anzi, ce ne sono infinite. Analogamente, se prendiamo due punti qualsiasi (che non siano agli antipodi), per loro passa una e una sola retta.

Non è difficile verificare che queste strane “circonferenze”, che chiamiamo, comunque, rette intrinseche (e lo sono a tutti gli effetti per noi), sono quelle più lunghe tracciabili sulla superficie e sono tutte della stessa lunghezza.

Per farlo, basta munirsi di una lunga fune e di fissarla in un qualsiasi punto della superficie, ad esempio P, come mostrato in Fig. 4 (a sinistra la visione da fuori).

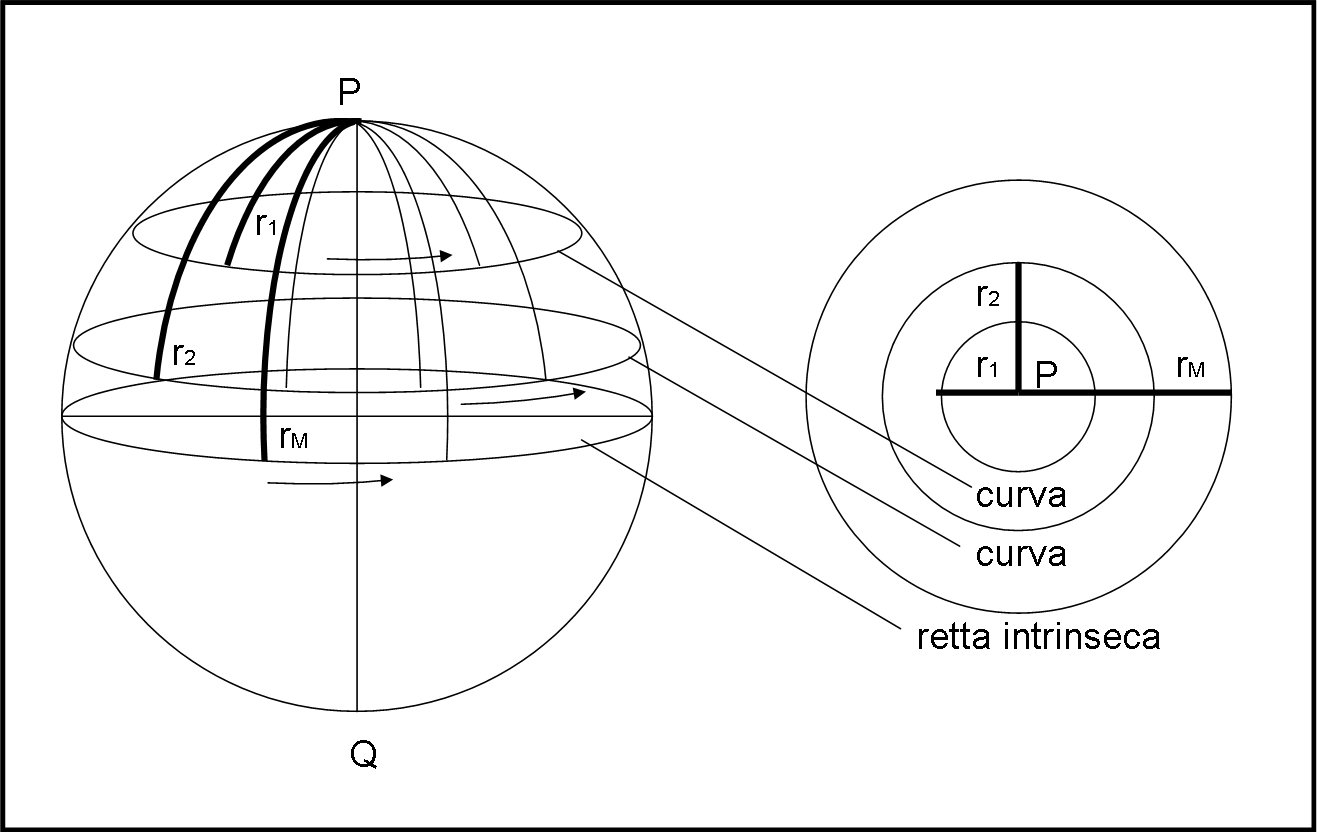
Teniamola ben tesa con una lunghezza uguale a r₁ e cominciamo a camminare (magari anche con il carrello per ulteriore conferma). Descriviamo una certa circonferenza che ha come raggio intrinseco (distanza tra circonferenza e punto P) proprio r₁. Il carrello ci conferma che è proprio una circonferenza intrinseca. Aumentiamo la lunghezza della corda fino a farla diventare r₂ e rifacciamo lo stesso esercizio, costruendo la circonferenza intrinseca di raggio intrinseco r₂. La circonferenza è più lunga di quella precedente. Proseguiamo fino a una certa lunghezza della corda r_M. Questa volta le cose cambiano e il carrello ci dimostra che stiamo percorrendo una retta intrinseca (anche se l’abbiamo disegnata come una circonferenza, dato che sappiamo che è una retta ma che è anche una curva chiusa).

Studiando meglio la situazione vediamo che la distanza tra P e la circonferenza, ossia r_M, è esattamente uguale alla distanza tra essa e il punto opposto di P, ossia Q (punto opposto di un punto è quel punto che sta proprio alla metà della retta intrinseca che passa da P e da Q, ossia la circonferenza sul piano del nostro foglio, a sinistra.

A questo punto, per puro scrupolo, ci possiamo portare su Q e rifare lo stesso lavoro fatto partendo da P. Il risultato è, ovviamente, identico a prima: la circonferenza che ha una lunghezza massima è quella con raggio intrinseco r_M, ossia la retta intrinseca (chiedete al carrello).

Notiamo anche che cambiando il punto P (e Q) possiamo descrivere tutte le rette e le circonferenze intrinseche della superficie.

L’esercizio appena svolto ci ha dimostrato che la lunghezza della retta intrinseca è la massima possibile e che, ovviamente,  il raggio intrinseco della retta (che è anche la circonferenza massima) è il più grande.

Il che vuol dire che qualsiasi circonferenza intrinseca tracciata sulla superficie ha lunghezza e raggio r minore di r_M.

Siamo di fronte a una situazione da un lato abbastanza imbarazzante, ma dall’altro molto elegante!

La retta è per noi un caso particolare di circonferenza, che mostra tutte le caratteristiche di non “piegare” mai. In fondo, non è una curva intrinseca (avrebbe tutte le caratteristiche della retta se non la percorressimo tutta o non mettessimo un segnale per riconoscere da dove siamo partiti). Tuttavia, per un abitante molto attento la sua vera struttura potrebbe anche essere riconosciuta.

Andiamo ancora oltre, rimanendo sempre sulla superficie (che fatica per noi che siamo tridimensionali…). Mettiamoci lungo una retta intrinseca dello spazio curvo a due dimensioni e disegniamo due punti A e B su di lei in Fig. 5 (a sinistra).

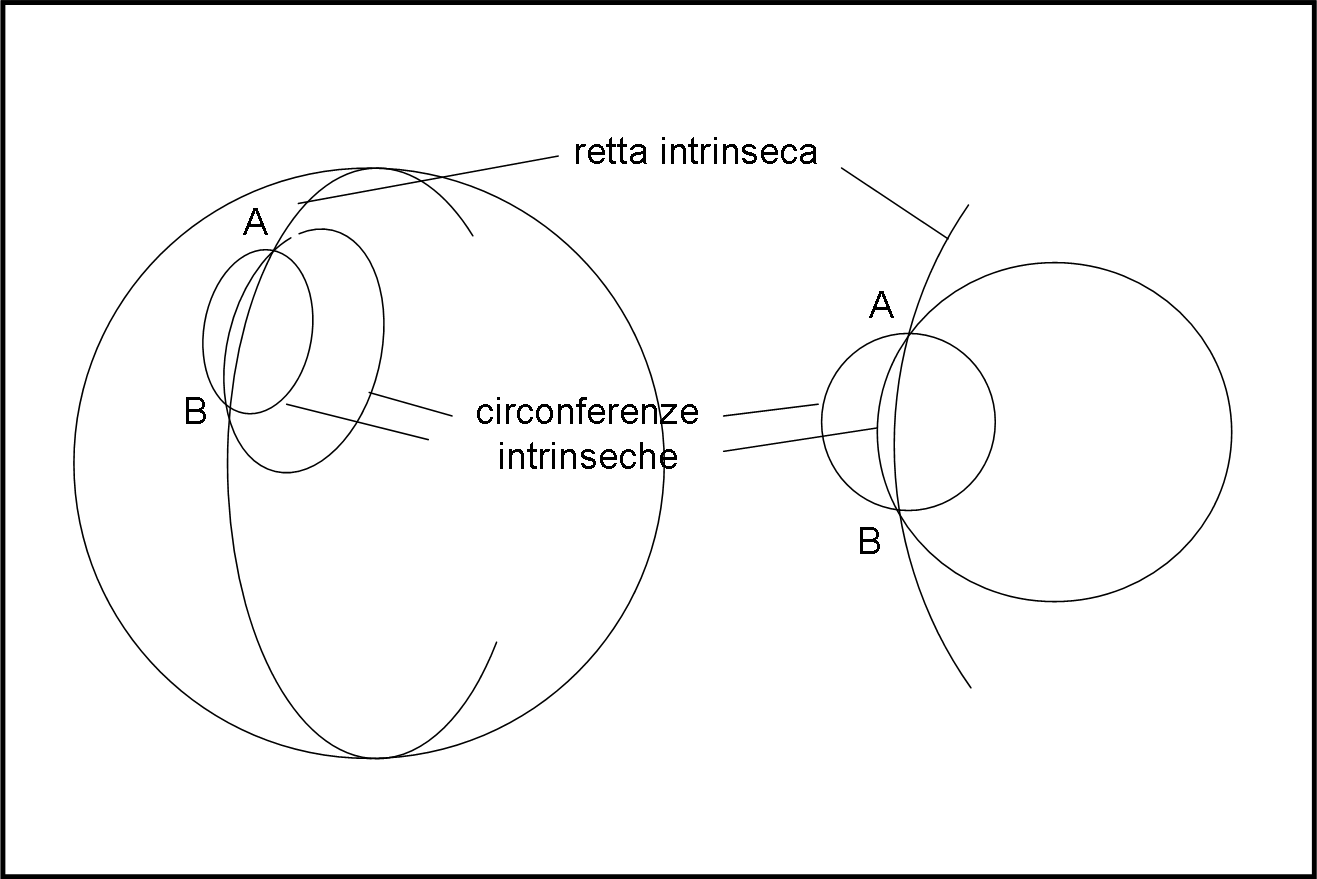
Adesso, possiamo provare ad andare da A a B in tutti i modi possibili, ossia seguendo altre linee, magari proprio archi di circonferenza come avevamo fatto nel piano. Possiamo sbizzarrirci quanto vogliamo, ma il risultato dovremmo già saperlo. La retta intrinseca è quella che ha il perimetro più lungo e quindi anche il raggio più grande. L’unica differenza, rispetto alla superficie piana, è che il raggio può diventare al massimo r_M e non infinito.

Tuttavia, essa rimane comunque la traiettoria con la curvatura minore tra tutte quelle possibili. Per analogia con quanto succede nel piano essa deve perciò fornire la traiettoria minima per andare da A a B. la retta intrinseca è una geodetica della superficie sferica. Una visione più intrinseca la vediamo nella parte destra della figura.

Abbiamo faticato un po’ e abbiamo forzato alcuni concetti per riuscire a dimostrare alcune caratteristiche essenziali della geometria sferica senza sfruttare la nostra capacità di avere una dimensione in più. Al limite, ci siamo fidati dell’intelligenza degli abitanti di “sferilandia” e della loro conoscenza delle regole euclidee.

Tutto diventa più semplice utilizzando una visione estrinseca. Tuttavia, aver lavorato solo su uno spazio a due dimensioni non euclideo (a parte le figure) ci ha sicuramente fatto entrare meglio nella problematica.