Indice di tutti gli articoli di Umberto presenti in archivio-Matematica

 

L'insieme R dei numeri reali non è numerabile.

Premettiamo che una caratteristica particolare di R è che può essere messo in corrispondenza biunivoca con un suo qualsiasi intervallo.Già Galileo aveva osservato che si possono mettere in corrispondenza biunivoca segmenti di lunghezza diversa, proiettandoli uno sull'altro.

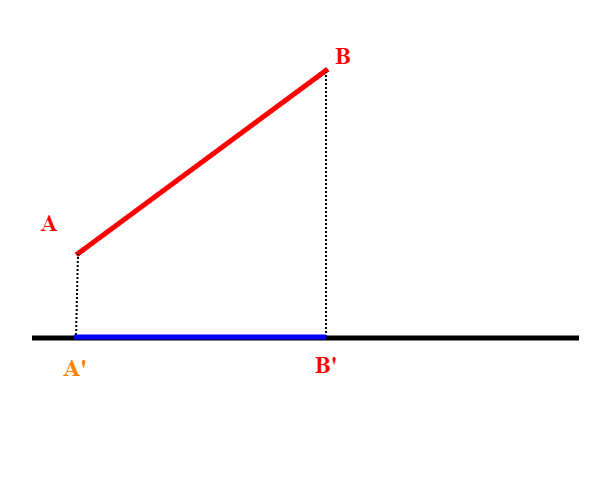
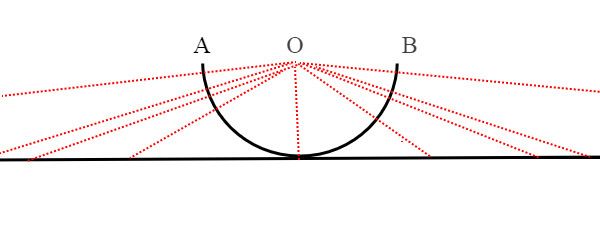
Se poi prendiamo  un  segmento di una certa lunghezza finita e lo incurviamo fino ad ottenere una semicirconferenza, e proiettiamo la semicirconferenza dal suo centro su una retta, otteniamo tutta la retta reale.

Queste sono cose intuitive, ma non si prestano molto a delle dimostrazioni rigorose. Vediamole nel caso di un intervallo aperto.In particolare vogliamo mettere R in corrispondenza biunivoca con [0,1] (è quello che ha fatto Cantor).Mi appoggio a degli argomenti presenti negli approfondimenti di matematica , che riguardano gli studi di funzioni.

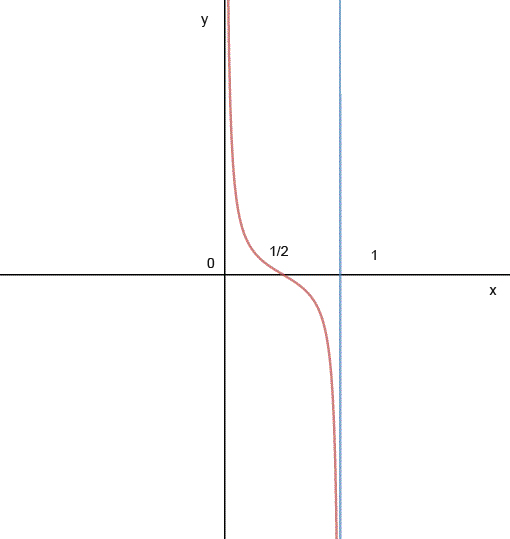
Consideriamo la funzione:

f:(0,1)---> R definita da: f(x)=

f(x) è una funzione ovunque definita in (0,1) dove è continua e derivabile;

f(x)= 0 per x=1/2; infatti

la funzione si azzera pertanto in 2x-1=0, quindi x=1/2

il numeratore è positivo per x>1/2; essendo x sempre maggiore di o, il denominatore è  sempre negativo in (0,1), quindi per 0<x<1/2 la funzione è positiva, per 1/2<x<1 la funzione è negativa.

consideriamo poi i due limiti negli estremi:

 ; se x tende a zero (dalla parte destra) 1/x-1 tende a 1, mentre sappiamo che 1/x tende a

 

; se x tende a 1,  dalla parte sinistra, 1/x tende a 1, mentre 1/x-1 tende a quindi la funzione ha due asintoti verticali; l'asse delle y (x=0) e la retta x=1.

(il segno dei due limiti si vede dal fatto che per x<1/2 la funzione è positiva, per x>1/2 invece è negativa)

La funzione (in (0,1)) è sempre strettamente decrescente; infatti la derivata prima   è sempre negativa (è la somma di due numeri al quadrato cambiati di segno)  quindi f è iniettiva (x1<x2 implica f(x1)>f(x2) , quindi f(x1)<>f(x2). Ma f non è né inferiormente né superiormente limitata, per quanto visto dai suoi due limiti negli estremi .Studiando graficamente la funzione,vediamo quindi  che assume  tutti i valori fra  , e quindi è suriettiva. Quindi l'intervallo (0,1) ha la stessa cardinalità di R.

Ma è così immediato dire che f assume tutti i valori reali? In realtà no, non è affatto banale. E' una conseguenza di un importante teorema sulle funzione continue, Il teorema dei valori intermedi.

Il teorema afferma che se una funzione è continua in un intervallo chiuso [a.b], supposto f(a)< f(b), allora assume tutti i valori dell'intervallo [f(a),f(b)]. Analogamente se f(a)> f(b), assume tutti i valori dell'intervallo [f(b),f(a)].

ma qui non siamo in queste condizioni, (0,1) è un intervallo aperto, allora a cosa serve?

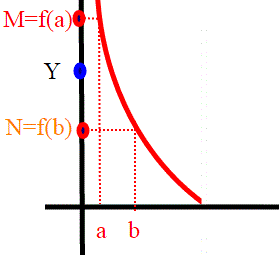
Consideriamo la figura:Sia Y un qualsiasi numero reale. Siccome f non è superiormente limitata , allora esiste un a tale che M=f(a) con M>Y; analogamente, essendo non inferiormente limitata, esiste un b tale che N=f(b)<Y. Se consideriamo l'intervallo chiuso [a,b] siamo nelle condizioni del teorema; f assume tutti i valori fra f(a) e f(b); in particolare anche il valore Y, visto che f(b)<Y<f(a). Quindi la nostra f assume tutti i valori reali. Abbiamo preso per buono il teorema dei valori intermedi; per chi vuole approfondire ho messo una appendice.

Confronto fra segmenti aperti e chiusi.

Vogliamo dimostrare adesso (per essere pignoli) che l'intervallo aperto (0,1) ha tanti punti quanti l'intervallo chiuso [0,1], e che quindi R ha tanti punti quanti l'intervallo chiuso [0,1].

(0,1) è contenuto in [0,1]: possiamo definire una funzione iniettiva

I:(0,1)---> [0,1] chè semplicemente  l'identità, ossia quella che ad x associa x . Non è però suriettiva , 0 e 1 sono punti non coperti da I.

esiste poi senz'altro una applicazione iniettiva f: [0,1]--->(0,1); per esempio f(x)=x/3 (se x1<>x2, x1/3<>x2/3)

Basandoci su queste due funzioni, vogliamo costruire un nuova funzione che chiamiamo g:[0,1]--->(0,1) in questo modo:

g(x)=x/3 se esiste n appartenente ad N tale che x=

g(x)=x altrove

Questa definizione divide l'intervallo in due insiemi complementari.

g(x) è iniettiva; infatti ci sono tre casi

1. x1 =, x2<>  ; in questo caso f(x1)=, f(x2)=x2 che è diverso da  qualsiasi sia n
2. x1<>, x2<>, x1<>x2 ; in questo caso si applica sempre la I, e quindi f(x1)<>f(x2)
3. x1<>, x2=  f(x2)=. f(x1)=x1 che è diverso da  qualsiasi sia n

La funzione f è anche suriettiva; se y appartiene a (0,1) abbiamo due casi:

1.  y= per qualche n; ma allora y=f()=1/3 * =
2.  y<>  qualsiasi sia n, ma  allora y=f(y)

Quindi R ha la stessa cardinalità di [0,1]

[0,1] non è numerabile.

Supponiamo che esista una corrispondenza biunivoca fra i Numeri naturali N e i numeri reali R. Vogliamo dimostrare che non copre tutto R, qualsiasi essa sia. Come sempre ci basiamo sul confronto fra cardinali, ci basta dimostrare che non esiste un funzione suriettiva di N-->[0,1].Infatti tale intervallo è un sottoinsieme di R,[0; 1] è equipotente a R. Per farlo consideriamo una qualsiasi successione di numeri reali. Cos'è una successione? è una funzione di N-->R, che in pratica etichetta i numeri reali con un certo numero naturale

Indichiamo con a1,a2,a3,...an i termini di  tale successione a valori in R. Vogliamo dimostrare che è impossibile che ricopra tutto l'intervallo [0,1]. Il metodo che adotto è differente dall'usuale metodo detto di diagonalizzazione di Cantor, che fa uso della notazione decimale di un un numero reale. Ci basta trovare un numero reale che appartenga all'intervallo [0,1] , ma che non appartenga alla successione.

Costruiamo una successione di intervalli I1,I2,I3,...In (chiusi, ovvero anche gli estremi appartengono all'intervallo) in questo modo:

Parto dall'intervallo  [0,1], e lo divido in tre parti uguali; sia a1 il primo termine della successione di numeri reali. Considero come I1 l'intervallo che non contiene a1 .Ce ne sono due di possibili, a patto che a1 non coincida con gli estremi. Abbiamo diviso l'intervallo in tre parti proprio per questo; nella peggiore delle ipotesi a1 appartiene a due intervalli contigui, ma allora prendiamo il terzo intervallo.

analogamente costruisco I2; divido in tre parti I1 e prendo uno degli intervalli che non contiene a2, che è il secondo termine della successione.Notiamo che oltre ad a2 , neanche a1 può appartenere ad I2.

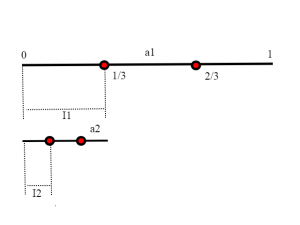
Chiaramente I1 contiene I2 per costruzione; Vado avanti così e costruisco I3,..In

Cosa hanno in comune tali intervalli? Sono in successione decrescente di inclusione; Il termine generico In non contiene nessuno dei termini a1,a2,a3,... an della successione. La lunghezza dell' intervallo  In non è altro che e ha come estremo inferiore 0. Intuitivamente l'intersezione di tutti gli In non è altro che un punto che chiamiamo a e che appartiene a [0,1]. Ma questo lo abbiamo anche  dimostrato rigorosamente nell'articolo precedente ; gli In sono una successione di intervalli incapsulati e l'estremo inferiore delle lunghezze è zero. Esiste dunque un punto a che appartiene a tutti gli intervalli.

Dunque a appartiene a tutti gli In, ma è diverso per costruzione da tutti gli an.

Quindi gli an non coprono tutti i numeri compresi in [0,1].

Si usa indicare con  c la cardinalità del continuo,  quindi aleph(0)<c

PS: la costruzione che abbiamo visto, quella di suddivisione degli intervalli, in modo leggermente diverso porta alla costruzione di un un insieme chiamato "insieme di Cantor" o anche "polvere di Cantor". Lo vedremo in seguito in modo più approfondito

 

Appendice

Premessa : una proprietà delle funzioni continue: la permanenza del segno.

Consideriamo una funzione f continua; essa avrà in un punto xo il valore del suo limite l (per x-->xo)

l=f(x0), vogliamo dimostrare  che in un certo intervallo contenente xo la funzione assume lo stesso segno del suo limite, che essendo f continua coincide con f(xo).

supponiamo f positiva (analogo discorso se negativa);

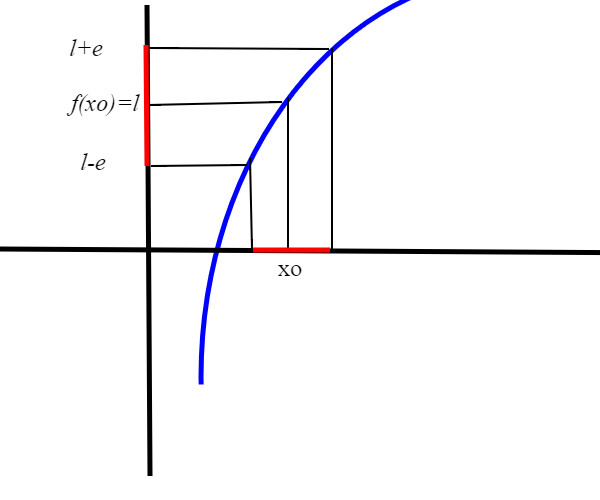
per la definizione di limite, qualsiasi sia e>0, f sarà confinata fra l-e<f(x)<l+e in un certo intervallo contenente xo; se prendiamo e=l/2, abbiamo l-e=l-l/2=l/2>0,  quindi l/2<f(x)<l+l/2=3/2l; quindi nell'intervallo la funzione assume tutti valori positivi, essendo l=f(xo)>0

Per dimostrare il teorema dei valori intermedi, è necessario conoscere il:

Teorema degli zeri

se f è una funzione continua su [a,b] e  si ha f(a)<0<f(b) allora esiste un punto in qui f si annulla.

Come vediamo l'enunciato è semplice, ed ha una forte valenza intuitiva. Noi abbiamo supposto f(a) negativo e f(b) positivo; la stessa cosa vale se f(a) è positivo, f(b) negativo.

Definiamo un insieme E={x appartenenti ad [a,b] tali che f(x)<0}

E contiene almeno a,quindi non è vuoto; E è superiormente limitato da b, quindi per l'assioma di completezza esiste xo=sup E<b;

supponiamo per assurdo che f(x) non si annulli mai in [a,b] allora in particolare anche f(x0) non si annulla ; ci sono allora due casi:

1. f(xo)<0;ma allora per la permanenza del segno della funzione continua f esiste un d tale che in (xo,xo+d)  (xo-d,xo+d)  [a,b]  sia f(x)<0; ma allora ci sarebbe un x>x0  appartenente a (xo,xo+d) in cui f(x)<0 contrariamente al fatto che xo è un maggiorante di E, cioè è  più grande di tutti gli x per cui vale f(x)<0
2. Premettiamo che qualsiasi x in [a,b] in cui f(x) >0 è un maggiorante di E. Supponiamo dunque f(xo)>0; sempre per la permanenza del segno allora esiste d tale che ogni x appartenente a (xo-d,xo)  (xo-d,xo+d)  [a,b] f(x)>0; quindi esisterebbe un x appartenente a (xo-d,xo)  minore di xo che sarebbemaggiorante di E perchè f(x)>0, contrariamente al fatto che x0, essendo sup E è il minimo dei maggioranti.

In entrambi i casi arriviamo a delle conclusioni false, perciò siamo partiti da un ipotesi sbagliata. Quindi f(x) si annulla in almeno un punto di [a,b]. Da notare ancora una volta l'importanza dell'assioma di completezza, che da quanto visto è alla base anche dei teoremi fondamentali dell'analisi matematica.

Dimostrazione del teorema dei valori intermedi

Dobbiamo dimostrare che comunque prendiamo un punto y0 interno ad [f(a),f(b)] esiste un xo appartenente all'intervallo [a,b] tale che la sua immagine sia yo, ovvero yo=f(x0) (abbiamo supposto f(a)<f(b); analogamente si procede nel caso contrario. Sappiamo dunque che f(a)<yo<f(b); definiamo una funzione g(x)=f(x)-yo; allora:

 

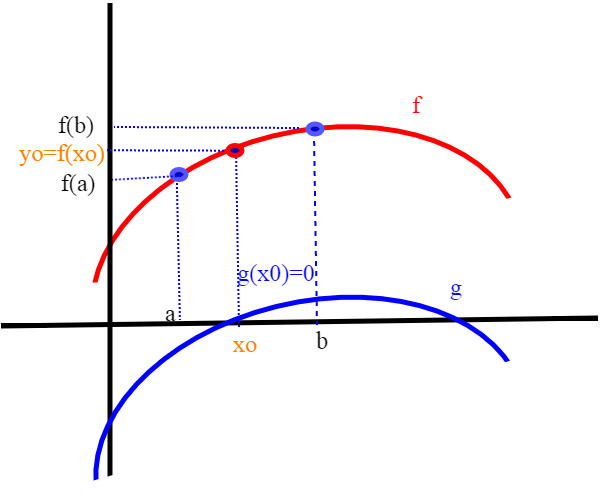
g(a)=f(a)-yo<0

g(b)=f(b)-yo>0; g è una funzione continua, perchè f è continua, dunque per il teorema degli zeri esiste un punto xo in cui si annulla. cioè g(xo)=0=f(x0)-yo; quindi yo=f(xo)