Mi sono accorto da poco che sul nostro circolo non avevo ancora parlato del metodo per determinare le “mie” care famiglie asteroidali. Lo riprendo dal vecchio sito, con qualche variazione, scusandomi con quelli che l’avevano già letto.

Le famiglie soggettive e oggettive (dal 1918 al 1990)

In questo articolo cerco di spiegare in modo semplice e approssimato il metodo usato, tanti anni fa, per definire, in modo finalmente oggettivo, le famiglie asteroidali. Spero anche che faccia capire l’estrema importanza di questi raggruppamenti che indicano eventi importantissimi nella storia del Sistema Solare. L’appendice riporta una soddisfazione molto … personale (di cui ho parlato anche QUI).

Ogni asteroide può essere considerato dinamicamente un pianeta a tutti gli effetti: rivolve attorno al Sole seguendo le leggi di Keplero o –meglio ancora- obbedendo alla legge di Newton. Ne segue che la sua posizione nel cielo è definita perfettamente una volta che sia conosciuta la sua orbita.

L’orbita non è però qualcosa di veramente fisso. In particolare, non sono fissi i parametri angolari, ossia l’argomento del perielio e la longitudine del nodo. Essi variano continuamente per effetto della precessione. In altre parole, essi assumono tutti i valori tra 0° e 360° nel giro di poche o tante migliaia di anni, a seconda della distanza dal Sole. In parole più vicine al nostro problema, due oggetti che partono anche molto vicini nello spazio, con il passare del tempo, subiscono una precessione leggermente diversa che porta le loro orbite a essere orientate in modo qualsiasi, anche se la forma rimane molto simile.

Analogamente, ha poco senso, per lo scopo che ci prefissiamo, considerare il tempo di passaggio al perielio. Che un oggetto passi al suo punto più vicino al Sole in una certa data o in un’altra non ha alcun interesse per la sua storia passata: dato che cambia il perielio, cambia anche il momento in cui viene raggiunto. Si può quindi concludere che gli elementi orbitali che caratterizzano completamente le posizioni relative degli asteroidi durante tutta la loro vita (tranne eventuali variazioni non dovute a collisioni reciproche) sono tre: semiasse maggiore, eccentricità e inclinazione.

Per guardare come essi si distribuiscono nello spazio, indipendentemente dal tempo che è passato da quando hanno iniziato la loro esistenza singola, si usano due classici diagrammi, molto semplici: eccentricità e inclinazione in funzione del semiasse. Tuttavia, le cose non sono così facili… Le perturbazioni causate dai pianeti maggiori inducono variazioni più o meno grandi anche su eccentricità e inclinazione. I valori che si osservano valgono per un certo istante, ma non su scale di tempo paragonabili alla vita dei piccoli pianeti.

Questo tipo di elementi orbitali, che si calcolano anche durante un breve periodo di tempo pari a poche rivoluzioni, vengono chiamati “osculatori”. Danno una certa idea della distribuzione degli oggetti della fascia asteroidale, ma subiscono le variazioni di eccentricità e inclinazione in funzione del tempo. Fortunatamente, queste variazioni possono essere calcolate dato che hanno un andamento periodico. In altre parole, eccentricità e inclinazione oscillano sopra e sotto un valore medio.

La meccanica celeste e i suoi grandi maestri sono stati in grado di ricavare questi valori medi, che portano velocemente a quelli finali che vengono chiamati “propri”. Essi sono valori che possono essere considerati fissi anche su scale di tempo dei miliardi di anni. Il primo passo da fare è quindi trasformare gli elementi osculatori in elementi propri.

A questo punto, abbiamo le orbite praticamente indipendenti dal tempo e quindi in grado di rappresentare veramente la distribuzione degli asteroidi nello spazio ipotetico formato dalle tre grandezze: eccentricità, inclinazione e semiasse maggiore. Di quest’ultimo non ho parlato, ma esso può considerarsi praticamente costante nel tempo. Per poterlo variare non bastano le perturbazioni planetarie, ma solo e soltanto azioni esterne come collisioni o -dinamicamente- condizioni estremamente particolari, come le immissioni all’interno delle risonanze con Giove.

Tuttavia, se un oggetto cade in queste “trappole” dinamiche, nel giro di pochi milioni di anni si trasferisce in zone diverse della fascia e quindi non compare tra quelli da analizzare. Per loro, poi, non ha nemmeno senso parlare di elementi propri.

Vediamo, allora, come si mostrano i diagrammi a-e e a-i per tutti gli asteroidi conosciuti (al posto di i si mette di solito il seno dell’angolo, sen(i), tanto è la stessa cosa). Le Fig. 1 e 2 si riferiscono alla popolazione che avevamo nel lontano 1990. Poche migliaia di oggetti a disposizione, ma più che sufficienti per una ricerca di tipo statistico.

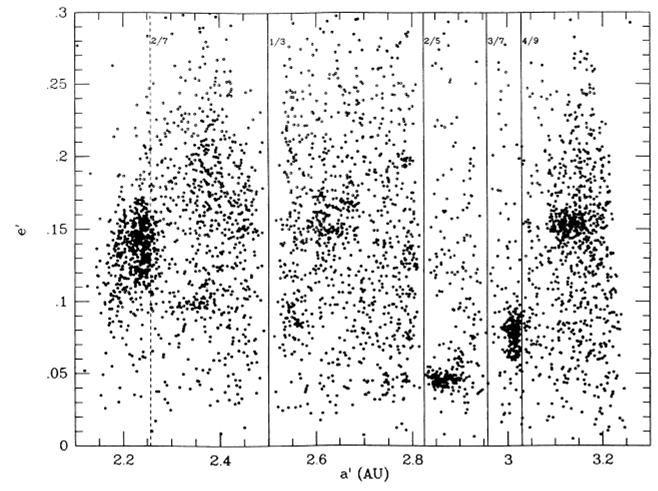
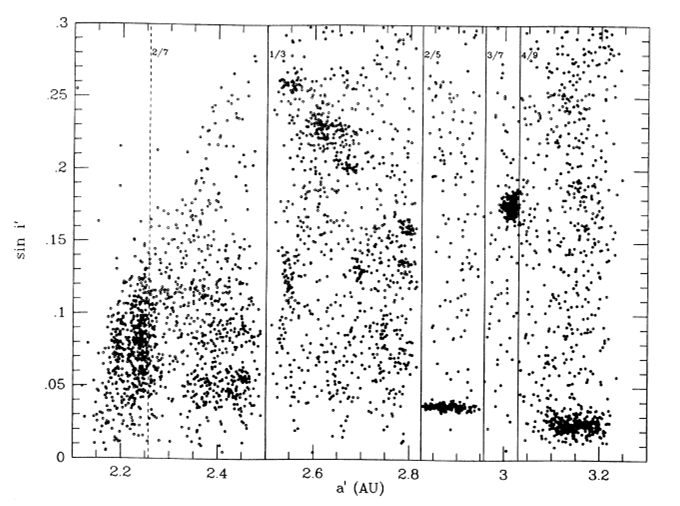
Risulta evidente, già ad occhio nudo, che vi sono qua e là dei raggruppamenti particolari, troppo densi per essere dovuti al caso. Pensate che qualcuno di questi era già stato localizzato dall’astronomo giapponese Hirayama nel lontanissimo 1918.

L’occhio è qualcosa di fantastico, ma non è in grado di stabilire in modo oggettivo cosa sia veramente distribuito in modo anomalo. E’ necessario stabilire un procedimento che riesca a dire, senza alcuna soggettività, cosa sia veramente un gruppo fuori dalla media e stabilire i suoi membri.

E qui per anni e anni è cascato l’asino! Si sono provati vari metodi, ma sempre basati, o all’inizio o alla fine, su una valutazione occhiometrica e non squisitamente matematica.

Vediamo allora le cose in modo un po’ diverso. Abbiamo a disposizione uno spazio a tre dimensioni che sono semiasse maggiore a, eccentricità propria e, e inclinazione propria i o sen(i). Ogni asteroide assume quindi una particolare posizione in questo spazio virtuale, che è definita completamente da una terna di valori a,e, sen(i). In uno spazio a tre dimensioni siamo, però, capaci di calcolare la distanza tra i punti.

Se le dimensioni fossero solo due (piano cartesiano x,y) si avrebbe:

d = (x² + y²)^1/2

Nelle tre dimensioni, in modo analogo:

d = (x² + y² + z²)^1/2

Potremmo, allora, porre x = a, y = e, z = sen(i) e calcolare la distanza tra due orbite asteroidali, che sono proprio definite dai tre elementi considerati.

Sì, sarebbe un bel passo in avanti, ma che senso avrebbe questa specie di “distanza” in uno spazio definito da tre elementi orbitali? fisicamente ben poco, dato che il semiasse maggiore a si misura in Unità Astronomiche, e non ha dimensioni, e i è un angolo.

E’ necessario, allora, fare un passo in più e capire bene cosa rappresentano le orbite di asteroidi molto simili tra loro. Dato che il caso non può certo spiegare raggruppamenti così ben visibili anche ad occhio e che la scoperta di nuovi asteroidi aumenta sempre di più la loro densità, non si può che concludere che la situazione si è venuta a creare attraverso un ben definito fenomeno o dinamico o fisico.

Processi di carattere dinamico possono spazzare via o anche concentrare oggetti, ma non sotto una certa distanza media. Per i gruppi di Hirayama non può funzionare. Deve, perciò, essere di tipo fisico. Non è difficile scoprirlo: le mutue collisioni.

Due asteroidi che si scontrano producono un insieme, anche enorme, di frammenti che rimangono su orbite molto simili tra loro. Come già detto varie volte, un urto può distruggere un oggetto ma non riesce a cambiare di molto la loro energia orbitale. Ne segue che i frammenti di una collisione devono avere orbite quasi identiche e gli elementi “fissi”  rispetto al tempo che li caratterizzano devono essere altrettanto simili. E’ ovvio, quindi, che ogni raggruppamento presente nello spazio dei tre parametri orbitali, considerati precedentemente, può essere considerato come l’insieme dei frammenti di una singola collisione catastrofica.

Sotto questa ipotesi, verificata attraverso molti studi di evoluzione fisica su cui abbiamo lavorato per anni, è allora possibile fare il seguente ragionamento: “Le differenze tra gli elementi orbitali dei frammenti di una singola collisione dipendono essenzialmente dalla velocità con cui i frammenti sono stati scagliati nello spazio (vero) a seguito dell’urto”. Purtroppo, però, noi abbiamo soltanto differenze di elementi orbitali. Come possiamo legarli alla velocità di espulsione, parametro veramente fisico e legato alla collisione?

Bene, ci aveva già pensato Gauss, o -almeno- ci aveva fornito delle equazioni che legavano le variazioni degli elementi orbitali alle velocità relative tra oggetti che percorrano due orbite relativamente vicine e viceversa.  In altre parole, le equazioni permettono di scrivere le velocità basandosi soltanto sugli elementi orbitali, assumendo che tutto sia nato da un singolo punto, ossia quello dove è avvenuto l’impatto.

Bellissimo, ma c’è ancora un problemino. Per scrivere le equazioni è necessario anche saper i valori dei parametri orbitali angolari all’istante dell’evento catastrofico. Infatti, se un oggetto si rompe vicino al perielio o vicino all’afelio le variazioni dei parametri orbitali cambiano e di conseguenza anche le velocità. In altre parole, una stessa velocità di espulsione causa variazioni orbitali maggiori o minori in punti diversi dell’orbita.

Purtroppo, l’istante dell’impatto non può dircelo nessuno. Possiamo però accontentarci di un approccio statistico. Al posto degli angoli “veri” al momento dell’impatto, possiamo mettere degli angoli “medi”, ossia angoli che rappresentino la posizione statisticamente più probabile lungo l’orbita. Non inserisco la formula finale, ma si può trovare andando all’articolo originale (QUI).

Non si può fare di meglio, ma, visto lo scopo statistico, il risultato non è molto diverso da quello reale.

Siamo finalmente riusciti a trovare una metrica speciale nello spazio degli elementi orbitali a,e e sen(i) che ci permette di stabilire una distanza che non sia un valore privo di senso, ma che sia strettamente legato alla fisica, ossia che rappresenti proprio la velocità di espulsione dei frammenti. In altre parole, un legame fisico tra i tre parametri orbitali.

Questa metrica ci fornisce un metodo del tutto oggettivo per stabilire le distanze tra i membri del gruppo (espresse in m/sec) e per poter calcolare quando un insieme di oggetti sia statisticamente e fisicamente valido.

Non ci resta che trovare un algoritmo che sia capace di raggruppare tra loro oggetti “apparentemente” vicini, la cui distanza sia definita dalla metrica definita prima.

Perché non rifarsi alla Natura e agli alberi (non sono poi cambiato molto rispetto ad oggi…)? Quello scelto è praticamente il sistema che permette di disegnare l’albero genealogico di una grande famiglia storica. Si parte dai figli viventi che si legano ai padri e alle madri che a loro volta si legano ai nonni e alle nonne e via dicendo fino ad arrivare ad … Adamo ed Eva! Nel nostro caso si parte dagli asteroidi più vicini tra loro e poi si costruisce l’albero che li unisce andando a distanze sempre crescenti.

Ed eccoci quindi al diagramma a stalattite che tanto mi è piaciuto.

Si comincia dalla punta della stalattite che indica la coppia di oggetti più vicini tra loro e poi, a mano a mano, si uniscono alla coppia, come un reticolato, altri oggetti con distanze via via più grandi. Crescendo la distanza ammessa, cresce velocemente anche il numero di “parenti” e, se arrivassimo fino a distanze enormi, tutti gli asteroidi si unirebbero tra loro. Bisogna quindi stabilire un limite al grado di parentela.

Senza scendere troppo nei particolari, cosa possiamo fare? Beh… immaginiamo che gli asteroidi assumano posizioni del tutto casuali e senza raggruppamenti anomali. Li prendiamo tutti e li mischiamo a caso, con un programma “random”. Lo facciamo varie volte in modo da avere una certa sicurezza. Dopodiché, utilizziamo, su questa popolazione artificiale, il metodo di raggruppamento ad “albero” genealogico. Troveremo la prima coppia che si unisce a una certa distanza,  ma è una coppia fittizia dovuta al caso e non a un’origine comune. La distanza  corrispondente (ossia la velocità relativa, ricordate?) può essere considerata come il livello di accoppiamento “random”. La Fig. 3 mostra, a sinistra, la vera distribuzione in una certa zona della fascia principale; a destra una simulazione “random”.

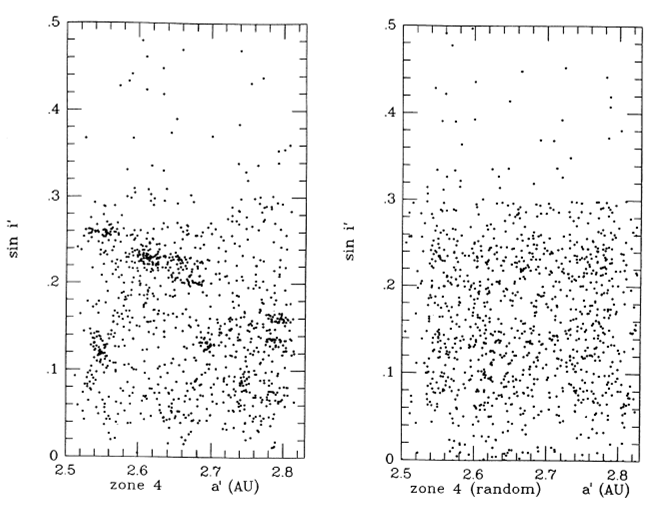
Valutiamo anche quante coppie nascono in funzione della distanza crescente e poi facciamo un po’ di calcoli statistici. Alla fine, possiamo definire un livello abbastanza preciso che ci dica quando troppi asteroidi iniziano a essere eccessivamente vicini rispetto a una popolazione senza vincoli di parentela. Questo livello lo chiamiamo livello “quasi-random” (dato che abbiamo eseguito alcune correzioni un po’ più sofisticate).

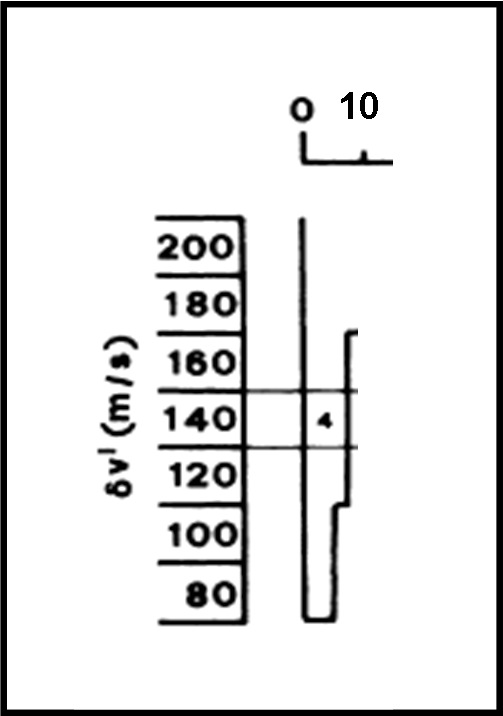
Torniamo, infine, alle stalattiti costruite con gli asteroidi veri e vediamo quali di esse superano come profondità il livello casuale. Queste stalattiti definiscono le famiglie asteroidali, ossia quei gruppi che hanno oggetti troppo vicini per essere dovuti al caso. Più le stalattiti sono profonde e più la famiglia è statisticamente valida. La Fig. 4 mostra alcune stalattiti e il livello quasi-random che identifica le famiglie più “serie”. In ordinata vi è la distanza (velocità) via via decrescente (verso il basso), in ascissa il numero di oggetti. Ogni stalattite, al livello quasi-random, riporta l’oggetto con il numero d’identificazione più piccolo.

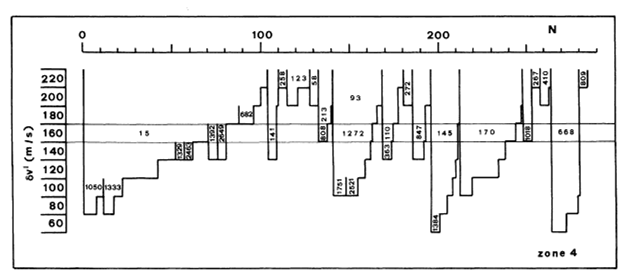
Finalmente, il gioco è fatto e non dipende assolutamente dalla soggettività di chi ha svolto il lavoro di raggruppamento. Non per niente, a distanza di 23 anni e con un numero di asteroidi dieci volte più grande, si è potuto tranquillamente proseguire con le stesse stalattiti precedenti. Esse sono cresciute perché si sono scoperti oggetti più piccoli che sono entrati tra i parenti stretti e si sono allungate perché le coppie molto vicine sono decisamente più frequenti e sempre più a contatto. Sarà anche variato il livello random (abbiamo aumentato il numero di oggetti presenti nello stesso spazio fisico), ma nettamente meno di quanto non siano scese le stalattiti reali.

Ne sono nate anche di nuove, formate essenzialmente da frammenti molto piccoli, magari associati a un asteroide molto grande. Siamo nel caso di una craterizzazione violenta e non di una vera catastrofe planetaria.

Come provare tutto questo procedimento essenzialmente dinamico e statistico a cui volevamo dare un significato fisico? Andare a vedere se i membri di una singola famiglia hanno tutti qualche caratteristica in comune (il taglio degli occhi, il naso a gobba, le orecchie a sventola, e mille altri particolari). WISE ne ha dato la conferma definitiva (vedi appendice), anche se molte prove erano già state rese possibili da progetti come IRAS.

Il successo più grande e affascinante? Prendere la famiglia di Vesta, l’unico oggetto classificato di tipo spettroscopico V, a causa delle sue caratteristiche fisico-chimiche basaltiche, e andare a vedere di che tipo sono i suoi frammenti stabiliti in base alla classificazione precedente. Sperare ardentemente che la maggior parte di loro risulti di tipo V, mai trovato altrove nella fascia asteroidale.

E così è stato! A questo punto è stato facilissimo legare i frammenti asteroidali a Vesta, andare a recuperare i NEA di tipo V (frammenti che sono finiti nelle risonanze con Giove e sono terminati tra i pianeti interni) e poi recuperare meteoriti anch’esse di tipo V. Quel pezzo di roccia che stringevamo tra le dita era sicuramente stato espulso molti milioni di anni prima da Vesta, quando si era formato il grande cratere che aveva creato la famiglia.

Che emozione, ragazzi! Un pezzo di asteroide tra le dita, sapendo esattamente il nome del “papà” che lo aveva mandato fino a noi attraverso un viaggio lungo e travagliato. Guardare Vesta al telescopio è diventato, da quel momento in poi, come salutare un amico fraterno.

La famiglia di Vesta trovata nel 1990 (su 4100 asteroidi totali) aveva solo 7 membri (rischiavamo grosso, eh?), quella trovata nel 1995 (su circa 12000 oggetti) ne aveva 231. Oggi, il nuovo lavoro arriva a più di 1331 membri (su 130 000 asteroidi considerati). La Fig. 5 mostra la piccola, ma significativa, famiglia del 1990 con i suoi 7 membri, tutti, però, di tipo V!

Non è difficile capire quante cose si possano fare con un gruppo che ha sicuramente un’origine comune. Cercare di ricostruire la distribuzione dei frammenti al momento dell’impatto, calcolare addirittura il punto dell’orbita in cui è avvenuto l’urto, stabilire, forse, anche l’epoca della distruzione. Ma anche calcolare quanti frammenti sono stati inviati dentro qualche risonanza vicina e sono diventati NEA, ricostruire i processi di frammentazione su oggetti di vari chilometri, determinare le proprietà rotazionali dei vari frammenti e del più grande, in parte accumulatosi nuovamente, studiare il trasferimento di momento angolare dovuto all’impatto, ecc., ecc.

Insomma, viva gli asteroidi, fossili viventi che ci raccontano il passato del nostro Sistema Solare!

Appendice: dopo 23 anni le “mie” famiglie tornano a vivere

Nel giro di pochi anni, eravamo riusciti ad applicare il metodo su poco più di 12000 asteroidi (quelli a disposizione). Avevamo anche previsto come si sarebbe potuto fare in futuro (quando il numero sarebbe cresciuto di molto) per evidenziare, attraverso le dimensioni e la posizione relativa, gli oggetti “intrusi” che si sarebbero venuti a trovare casualmente nelle stesse zone delle famiglie, ma che niente avevano a che vedere con le distruzioni catastrofiche che avevano originato i veri raggruppamenti.

Un metodo veramente “banale”, ma molto robusto. Bastava inserire, in un diagramma che avesse in ascissa la velocità relativa (legata ai parametri orbitali) e in ordinata il diametro (o, in mancanza di questo, la magnitudine assoluta), gli asteroidi che sembravano appartenere statisticamente a un’unica famiglia e guardare se qualcuno di loro risultava in una posizione del tutto anomala. Ricordiamo, infatti, che una collisione più o meno catastrofica comporta una distribuzione delle velocità di espulsione dei frammenti tale da inviare più lontano gli oggetti più piccoli e mantenere, relativamente vicini al pezzo più grosso rimasto, quelli più grandi.

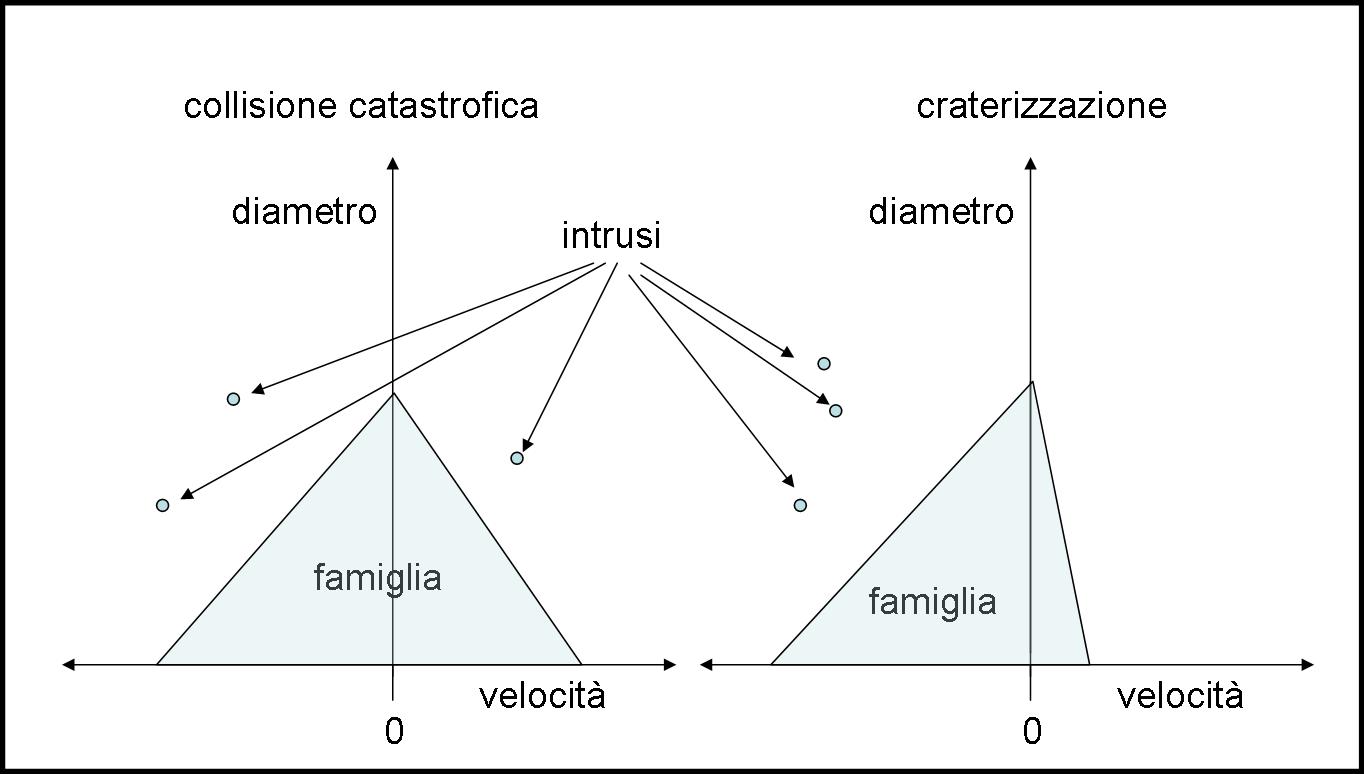
Insomma, un diagramma  a triangolo, più o meno isoscele. In particolare, se la collisione fosse veramente catastrofica il triangolo sarebbe molto regolare (espulsione in tutte le direzioni); se, invece, fosse una semplice craterizzazione, si vedrebbe un oggetto grande e tutti gli altri disposti lungo una sola direzione. Gli oggetti “vagabondi” erano sicuramente degli intrusi. Se poi si aveva anche la conferma spettroscopica, ancora meglio. La Fig. 6 mostra il metodo di riconoscimento degli intrusi in modo molto schematico.

Purtroppo, il numero di asteroidi non era cresciuto abbastanza per ripetere il metodo, gli elementi propri non erano ancora disponibili, altri impegni erano intervenuti  e poi … sono andato in pensione.

Potete, allora, immaginare il mio interesse quando ho letto, nel 2013, che, a seguito della missione WISE, era stato finalmente possibile ottenere una stima delle dimensioni di circa 120 000 asteroidi. Un gruppo di ricercatori aveva deciso di analizzare questi oggetti e allargare il numero delle famiglie e valutarne i possibili “intrusi” attraverso l’albedo misurato e quindi le dimensioni.

Indovinate che metodo hanno usato? Proprio il mio, con tanto di metrica e di diagrammi a stalattite. Per non dire delle figure con il diametro in funzione del semiasse orbitale che avevo ipotizzato come risolutive tanti anni prima.

Insomma, mi è quasi sembrato che la matita e il programma che avevo “posato” tanti anni prima fossero stati ripresi da nuovi ricercatori che ancora oggi si fidavano di quello che avevo prospettato e messo in pratica su un numero ben minore di oggetti. Non posso nascondere un senso di orgoglio, ma, soprattutto, di appagamento scientifico, vedendo che il lavoro fatto un tempo poteva ancora essere utile oggi, con i nuovi strumenti ben più tecnologicamente avanzati. Peccato, soltanto, che non era il gruppo di Torino ad averlo fatto… ma, si sa, la riconoscenza è una parola poco conosciuta.

Vedere citati nel nuovo lavoro apparso su Astrophysical Journal molti dei lavori pubblicati dal mio gruppo di Torino, a volte insieme a collaboratori stranieri, mi dà ancora oggi una certa emozione. Soprattutto pensando che sono passati 23 anni e che sembra mi sia messo di nuovo in azione.

Ricordi di un vecchio astronomo, anzi planetologo…

Non ho molto altro da dire. Abbiamo già parlato di famiglie asteroidali e dell’importanza che hanno non solo per studiare l’evoluzione collisionale degli asteroidi, ma anche l’origine e i meccanismi dinamici di trasferimento dei loro frammenti diventati, alla fine, proprio quegli oggetti “pericolosi” per la Terra che tutti i giornali ricordano soltanto quando qualcuno di loro viene a sfiorare il nostro pianeta.

Spero che perdoniate questo articolo che pecca un po’ dell’umiltà che vado sempre predicando. Ma quando ci vuole ci vuole!

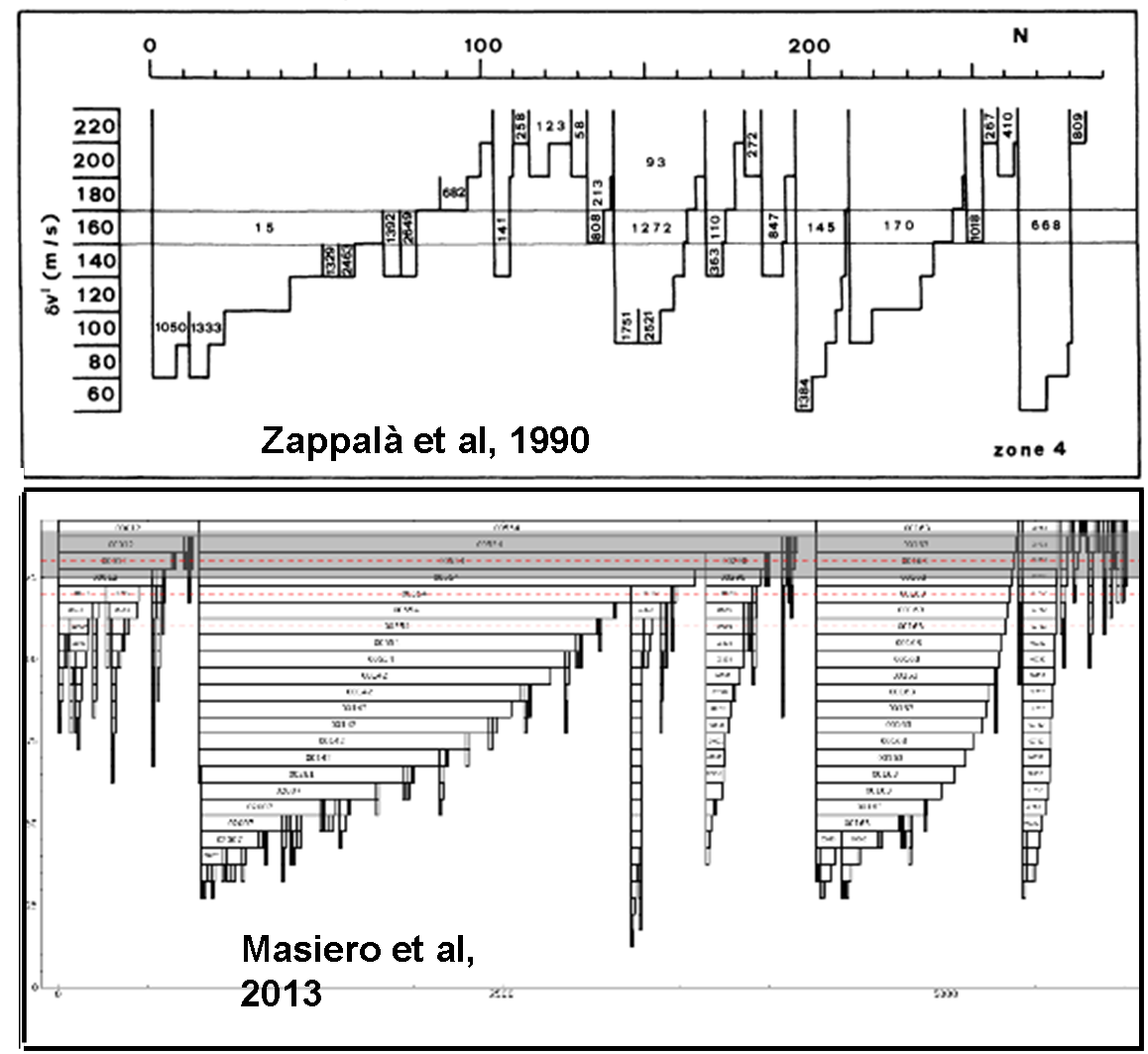
Allego in Fig. 7, una delle figure del lavoro originario del 1990 e una di quelle del nuovo articolo del 2013. Le stalattiti si sono allungate al passare del tempo, ma sono sempre loro…

Articoli originali QUI (1990) e  QUI (2013)

Per approfondire la conoscenza degli asteroidi, potete leggere QUI, QUI e QUI ed i link correlati.