Categorie: Fisica classica
Tags: ombra raggi luminosi trigonometria velocità
Scritto da: Vincenzo Zappalà
Commenti:48
Soluzione della “cosa” più veloce della luce: il vero QUIZ comincia adesso ****
Beh… Gianni ha dato la risposta esatta alla parte “facile” e SMA ha subito confermato, facendo un esempio apparentemente azzeccato. L’ombra di qualcosa si allunga in modo rapidissimo, nettamente e apparentemente ben più di quanto non possa fare la luce. Tutto risolto? NO! Il vero QUIZ comincia adesso!
Bene, vediamo di dimostrarlo con un semplice esperimento geometrico.
Consideriamo la Fig. 1.
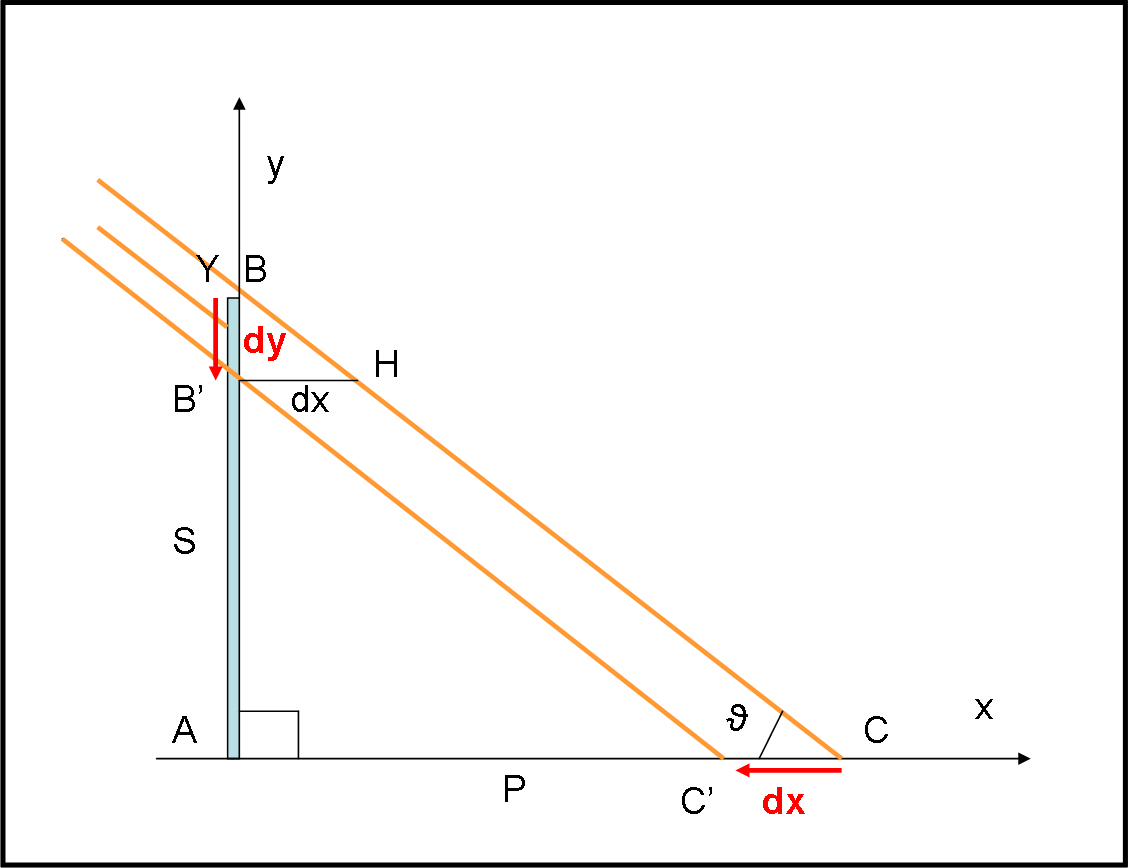
A sinistra vi è uno schermo S che può abbassarsi alla velocità che vogliamo. Esso viene investito da un fascio luminoso i cui raggi sono paralleli tra loro (sorgente molto lontana). L’ombra relativa allo schermo S si allunga sul pavimento P. Poniamo l’asse x lungo il pavimento e l’asse y lungo lo schermo. Schermo e pavimento sono perfettamente perpendicolari tra loro. Immaginiamo una situazione statica. Il primo raggio che oltrepassa lo schermo sfiora il punto B e giunge in C. L’ombra copre esattamente la linea AC. Sia, inoltre, BCA = ϑ l’angolo di inclinazione dei raggi rispetto al pavimento.
Scriviamo una semplice relazione tra i cateti del triangolo rettangolo BAC:
BA/AC = tan(ϑ)
Chiamiamo BA = Y e AC = X
Y/X = tan(ϑ)
Ricaviamo la lunghezza dell’ombra in funzione dell’altezza dello schermo:
X = Y/tan(ϑ) = Y cot(ϑ)
Abbiamo soltanto richiamato la funzione cotangente (QUI) che altro non è che l’inverso della tangente o, se preferite, il rapporto coseno/seno. Per semplicità chiamiamola solo cot e non cotan
Per adesso abbiamo fatto un confronto tra lunghezze…
Passiamo adesso al calcolo delle velocità. Abbassiamo lo schermo di una quantità dy (BB’). Ne segue che anche l’ombra si accorcia e il suo punto estremo passa da C ad C’, ossia percorre uno spazio dx. I triangoli ABC e BB’H sono ovviamente simili e vale immediatamente la relazione:
dx = dy cot(ϑ)
Ricordiamoci, adesso, una vera banalità: la velocità è data dal rapporto tra lo spazio percorso e il tempo impiegato a percorrerlo.
Noi sappiamo perfettamente quanto vale la velocità di abbassamento dello schermo vS. Essa è data da:
vS = dy/dt
Analogamente si può calcolare la velocità dell’ombra vO:
vO = dx/dt = dy cot(ϑ)/dt = vS cot(ϑ)
Come abbiamo detto precedentemente, la velocità di abbassamento dello schermo può essere scelta a piacere. Per non fare torto ad Einstein (un pochino sì perché ha una massa…), immaginiamo di abbassarlo alla velocità della luce (ma potremmo anche abbassarlo a una velocità di poco inferiore… e sarebbe più contento).
La relazione precedente si riduce (ponendo vS = c = 1) a:
vO = cot(ϑ)
Non ci resta che fare qualche conto o, ancora meglio, disegnare, in un grafico, vO in funzione dell’angolo ϑ, che può variare tra 0° e 90°, per costruzione. Vediamo, perciò, in Fig. 2, come varia vO in funzione dell’angolo di inclinazione dei raggi, avendo posto c = 1.
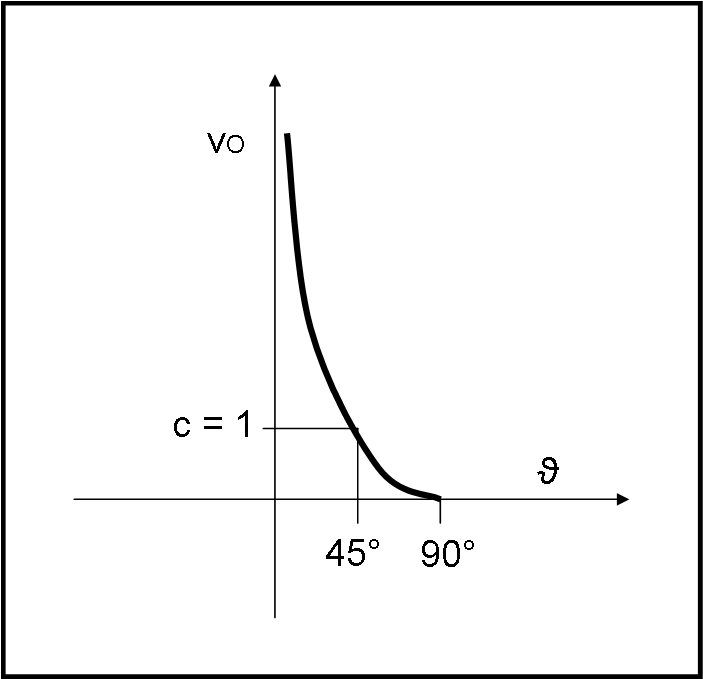
Non è difficile concludere che per valori di ϑ inferiori a 45° la cotangente è maggiore di 1 e quindi la velocità dell’ombra supera la velocità della luce. Addirittura tende a infinito (singolarità!) per ϑ che tende a zero (ombra estremamente radente).
Per capire il perché, basta disegnare in Fig. 3, il sistema “schermo - luce - pavimento” con angoli diversi. Se l’angolo è minore di 45°, l’ombra supera lo scorrimento dello schermo. Se l’angolo è maggiore di 45,° l’ombra diventa più piccola, fino a diventare ZERO per un angolo di 90° (chiedete ad Eratostene e ai suoi pozzi…). L’ombra tende, invece, a infinito per angoli vicini a zero.
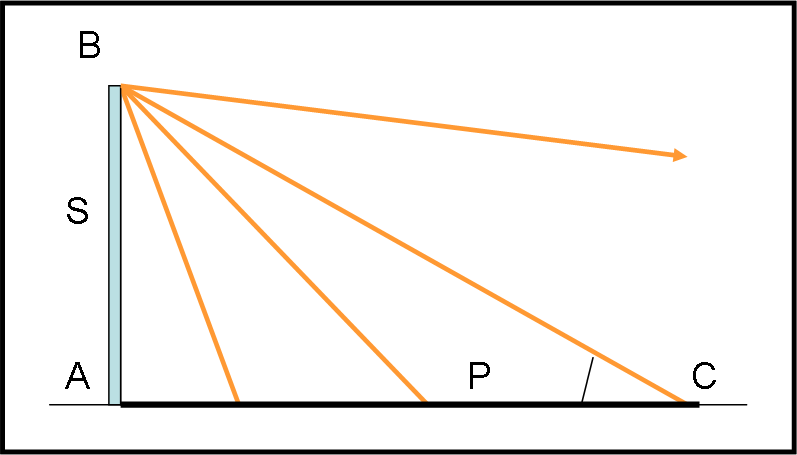
In realtà, se i raggi diventano quasi paralleli al pavimento sembra proprio che l’ombra si proietti (potendola vedere) attraverso l’intera galassia, e anche oltre, in un attimo. Quasi meglio che le particelle “entangled”.
A questo punto sarebbe ovvio costruire un racconto di fantascienza (che ho già in testa e che fa uso di una nuova particella che romperebbe la simmetria… forse proprio la particella della materia o energia OSCURA…).
Tuttavia, prima di andare avanti, rileggiamo bene quanto è stato scritto fin qui… Abbiamo fatto un ERRORE MADORNALE. Va subito corretto. Il bello è, però, che anche correggendolo, il risultato non cambia di molto e se ne vedranno delle belle…
A voi scoprire l’errore e continuare nella nostra avventura…
QUIZ iniziale QUI
Soluzione finale QUI






48 commenti
Caro Enzo, innanzitutto mi complimento con Gianni e con SMA che hanno risolto la prima parte del quiz…
Io non c’ero arrivato…. Eppure potevo pensare al ritornello della canzone di de Andrè: all’ombra dell’ultimo sole…
Guardando la seconda parte, così di fretta, ma bisognerebbe ragionarci con calma, quello che a me pare non funzionare è il tempo…
Provo a spiegarmi meglio..
Ammettiamo che in B e in C siano posizionati due orologi sincronizzati.
Al tempo T0 lo schermo è fermo con la sua estremità in B e la sua ombra giunge in C.
Quando l’orologio segna T1, lo schermo ha raggiunto la posizione B’, ma l’ombra non è ancora arrivata in C’, poiché la luce (prima bloccata) che ora lambisce l’estremità B’ dello schermo impiega un certo intervallo di tempo per raggiungere l’asse x, per cui quando l’ombra raggiunge C’ l’orologio segna un tempo un pochino maggiore rispetto a T1..
Paolo
la strada è quella buona....
ho dei dubbi anche io Come Paolo; qui in pratica abbiamo considerato infinita la velocità della luce, che in realtà non lo è; questo nel calcolo della relazione fra le due velocità tramite l'angolo; bisognerebbe provare a fare dei conti con una velocità finita; può anche darsi che la relazione venga uguale lo stesso
bravi, bravi.... agite, agite.... voi siete in grado di farlo!
complimenti a Gianni, io non c'ero arrivato.
In effetti quanto ci dice Paolo e' giusto... la luce ci impiega un certo tempo a raggiungere il piano su cui e' proiettata l'ombra, per cui c'e' un certo ritardo... e perche' noi si possa vedere l'ombra spostarsi deve anche tornare indietro.
Credo pero' che questo sia irrilevante, perche' a noi interessa la velocita' di spostamento dell'ombra... e questo dipende solo dalla geometria, non dal ritardo con cui noi la vediamo. Ad intuito e' un po come quando teniamo in mano una canna ferma da cui esce acqua ad una certa velocita': l'acqua colpisce un punto sul prato... quando noi ruotiamo la canna l'acqua colpira' per un po' lo stesso punto (cioe' c'e' un ritardo, dovuto alla velocita' dell'acqua), ma trascorso quello la velocita' di spostamento di quel punto sul prato non dipende piu' dalla velocita' dell'acqua, ma dalla velocita' di spostamento della nostra mano per il raggio...
occhio ai punti di partenza e di arrivo... le condizioni non sono le stesse...
Provo così:La relazione geometrica fra dx e dy è la stessa;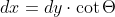 , il tempo totale dt però aumenta tenendo conto della velocità di propagazione della luce; al tempo dt di apertura della saracinesca di un dy bisogna sommare quello che la luce impiega per percorrere il tratto dato dalla differenza fra le due posizioni,
, il tempo totale dt però aumenta tenendo conto della velocità di propagazione della luce; al tempo dt di apertura della saracinesca di un dy bisogna sommare quello che la luce impiega per percorrere il tratto dato dalla differenza fra le due posizioni, 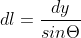 ovvero
ovvero 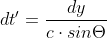 ;
;
lascio il quiz aperto per qualche giorno... va pensato molto bene...
Caro Enzo spero di non aver preso un abbaglio... perchè ho trovato un risultato che non mi aspettavo....
perchè ho trovato un risultato che non mi aspettavo....  quindi prima di proseguire alla ricerca di una funzione ad hoc, preferisco esporre il mio tentativo...
quindi prima di proseguire alla ricerca di una funzione ad hoc, preferisco esporre il mio tentativo...
Ho volutamente usato un caso limite, quello con l'angolo ϑ uguale a 45°...
In questo caso applicando le considerazioni geometriche esposte nell'articolo:
dx = dy cot (ϑ)
ma con (ϑ) = 45°
cot (ϑ) = 1
dx = dy
Bene ora invece cerco l'intervallo di tempo che misura un osservatore che si trova in C.... confrontandolo con quello di chi si trova in B....
Per chi si trova in B l'intervallo di tempo è t1 - t0..... per chi si trova in C bisogna tener conto che per lui l'ombra comincia a restringersi al tempo iniziale t0 + S0/c (dove S0 è il percorso della luce da B a C), mentre quando l'orologio di B segna il tempo t1, quello di C deve tener conto del percorso della luce S1, tra B' e C' (più breve del precedente) e il cronometro segna t1 + S1/c...
Nella figura ho provato ad illustrare il procedimento.
In pratica anche con un angolo (ϑ) di 45° la velocità dell'ombra V0 misurata dall'osservatore di C è più alta di Vs, e se questa vale C è maggiore di quella della luce..
Mi fermo qui, per ora... prima di affrontare un caso con (ϑ) qualsiasi, preferirei capire se sono fuori strada oppure...
Paolo
vai pure avanti con un angolo qualsiasi. Per avere una funzione più maneggiabile e interessante UN CONSIGLIO PER TUTTI: non prendete c come velocità di scorrimento dello schermo (cosa in realtà impossibile), ma un valore ac, dove a < 1. Avrete così un nuovo parametro per giocare alla fine...
Tra non molto ce la farete....
Vabbè allora prova a proseguire... a mio rischio e pericolo...
Si tratta di pochi passaggi logici e qualche passaggio matematico (che poi siano corretti si vedrà... ).
).
Innanzitutto per non confondersi con i segni (positivo o negativo), contrariamente a quanto riportato nella figura che ho postato :
:
dx = (X0-X1) e dy (Y0-Y1).... così hanno segno positivo
Dunque: Vs = dy/dt e Vo = dx/dt'
dt' = (t1 + S1/c) – (t0 + So/c) = (t1-t0) + (S1-So)/c
dt' = dt + (S1-S0)/c
Per il teorema di pitagora: S² = Y² +X² e quindi S = √(Y² +X²)
Ne segue che:
S1 = √Y1² +X1²........
ma X1 = Y1 cot ϑ
S1 = √(Y1² +Y1² cot² ϑ) = √(Y1² (1 + cot² ϑ)........ porto Y² fuori dalla radice quadrata
S1 = Y1 √(1 + cot² ϑ)
analogamente:
So = √Yo² +Xo²
So = Yo √(1 + cot² ϑ)
quindi tornando a dt' e sostituendo : S1 e So
dt' = dt + (Y1 √(1 + cot² ϑ) -Yo √(1 + cot² ϑ))/c
dt' = dt + (Y1 -Yo) √(1 + cot² ϑ))/c
ma (Y1 -Yo) = - dy
Dato che Y1 è minore di Yo questa volta il segno di dy è negativo
dt' = dt - dy √(1 + cot² ϑ)/c
dt' = (dt c - dy √(1 + cot² ϑ))/c
Vo = dx/dt'
sostituisco dt' e dx= dy cot ϑ
Vo = dy cot ϑ/(c dt -dy √(1 + cot² ϑ))/c
Vo = c dy cot ϑ/(c dt -dy√(1 + cot² ϑ))..... divido sopra e sotto per dt
Vo = c dy/dt cot ϑ/(cdt /dt - dy/dt √(1 + cot² ϑ))
ma dy/dt= Vs
Vo = c Vs cot ϑ/(c -Vs √(1 + cot² ϑ)).
Se Vs = ac......... con a <1
Vo = c ac cot ϑ/(c -ac √(1 + cot² ϑ)).
Vo = c² a cot ϑ/c (1 -a √(1 + cot² ϑ)).
Vo = c a cot ϑ/(1 -a√(1 + cot² ϑ))......
Se voglio rappresentare la velocità come multiplo o sottomultiplo di quella della luce, basta porre
c = 1
Vo = a cot ϑ/(1 -a √(1 + cot² ϑ)
Non so a me sembra che il ragionamento fili, ma magari commesso qualche errore logico o matematico...
Paolo
Caro Paolino,
come già detto preferisco aspettare un po'... Un consiglio, però, te lo do: cerca di compattare un po' la formula finale, sapendo che cot = cos/sin .... Così, tanto per passare il tempo...
...In effetti è ulteriormente semplificabile...
Vo = a (cos ϑ/sin ϑ)/(1 -a√(1 + cos² ϑ/sin² ϑ )
Vo = a (cos ϑ/sin ϑ)/(1 -a√(sin² ϑ + cos² ϑ/sin² ϑ )
ma sin² ϑ + cos² ϑ = 1
Vo = a (cos ϑ/sin ϑ)/(1 -a √1/sin² ϑ )
Vo = a (cos ϑ/sin ϑ)/(1 -a/sinϑ )
Vo = a (cos ϑ/sin ϑ)/(sinϑ -a)/sinϑ
Vo = a cos ϑ/(sinϑ -a)
Paolo
non è una brutta funzione... direi... si potrebbe vedere come si comporta al variare dei parametri (a e teta), ad esempio. Magari anche con a = 1... sempre che sia giusta, sarebbe molto divertente....se no sarebbe lavoro sprecato
 sono proprio cattivo, eh?
sono proprio cattivo, eh? 
… tanto ci sto stavo già lavorando... ma pensavo di fissare a = 0,9, così Einstein non si arrabbia e vedere come varia Vo al variare di ϑ...
ma pensavo di fissare a = 0,9, così Einstein non si arrabbia e vedere come varia Vo al variare di ϑ... 
Paolo
è bello anche far variare a.... fidati...
Vabbè, se la funzione trovata non è corretta, comunque ha un comportamento simpatico.. .
.
Stavolta solo figure... solo curve che rappresentano l'andamento della funzione (se non ho sbagliato la rappresentazione), ossia come cambia V0 al variare dell'angolo teta (inclinazione con cui i raggi giungono al suolo) oppure al variare di a, ossia della Velocità Vs rapportata a quella della luce...
Dapprima ho rappresentato come varia V0 (velocità ombra) al variare dell'angolo Teta.
Nei due grafici, cambia il valore di a (0,1 e 0,3, quindi Vs= 0,1C e 0,3C).
Le velocità sono rappresentate con c=1, quindi Vo=1 significa che l'ombra viaggia alla velocità della luce, mentre V0= 10 significa che viaggia 10 volte più veloce della luce.
Due rami di un'iperbole...
Ovviamente più l'angolo teta è piccolo più la velocità dell'ombra tende a infinito..
La velocità negativa è quella che fin da subito mi ha stupito ... presumo che in tal caso l'ombra comincia a disgregarsi non dal vertice ma in senso inverso... (la causa è il diverso percorso, più breve o più lungo che deve compiere la luce).
... presumo che in tal caso l'ombra comincia a disgregarsi non dal vertice ma in senso inverso... (la causa è il diverso percorso, più breve o più lungo che deve compiere la luce).
Nella seconda figura cambia solo il valore di a.
Anche in questo caso in alcuni punti la funzione e quindi la velocità dell'ombra V0 tende a infinito oppure a meno infinito.
Infine con a=0,9 e a = 1 (ipotesi che farebbe arrabbiare Einstein..)
Con a=1 c'è solo il ramo negativo dell'iperbole... tra l'altro quando teta raggiunge i 90°, la funzione restituisce uno 0/0....
Segue (per evitare il limite di immagini)
Ho anche provato a mantenere costante l'angolo teta e vedere come cambia V0 in funzione di a.
Nei primi due grafici, cambia solo il valore dell'angolo teta...
Di nuove due rami di un'iperbole
Infine con altri valori di Teta....
Certo, che se la funzione è quella giusta all'ombra ne succedono delle belle...

Paolo
I valori negativi sono proprio dovuti a ciò che dici: arriva prima la luce della parte vicina e poi di quella lontana. Si vede prima quello che succede dopo...
E perché la cosa non funziona se invece di abbassare lo schermo, lo alziamo??? Sempre che sia giusta la formula...
Penso che questo fatto si ricolleghi al segno dei dt per il calcolo della Vo; è proprio quello che succedeva nella mia formula che era sbagliata e non mi dava singolarità, per un segno variazionale sbagliato; se lo schermo si alza la variazione dei due tempi ha lo stesso segno, è se si abbassa che ha variazioni di segno opposti che possono portare a singolarità per valori dell'angolo uguale a arcin(a) e poi a inversionii di segno. Ho corretto la formula e diventa come quella di Paolo.. penso siano giuste.
speriamo... ma qualcosa mi dice di sì.... fai qualche prova anche tu con qualche grafico, magari con lo schermo che si alza...
Vorrei ancora aspettare a dare la soluzione "ufficiale" per eventuali ripensamenti e/o aggiunte di "coraggiosi"...
Se lo schermo si alza, non solo la velocità V0 è sempre positiva, ma è sempre inferiore a Vs...
La figura riproduce il caso limite con a=1 (Vs = C) e ϑ = 45° (ossia cot ϑ = 1).
E' evidente che dal tempo t0 in avanti per l'osservatore in C, si aggiunge un tempo crescente dovuto al maggior percorso che impiega la luce (prima si guadagnava tempo ora si perde tempo..), per cui dt' è sempre maggiore rispetto a dt.
Usando gli stessi passaggi matematici di prima, questo cambio di segno si traduce nella funzione:
Vo = a cos ϑ/(sinϑ +a)
Solo nel caso limite di un angolo teta di 0°, V0 può raggiunge la velocità della luce... ma si tratta di un caso limite, poiché con un tale angolo l'ombra può raggiungere il suolo solo all'infinito (proprio come due rette parallele che possono congiungersi solo all'infinito).
Paolo
La funzione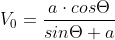 in
in  (schermo che si alza) è sempre decrescente , in modo molto blando
(schermo che si alza) è sempre decrescente , in modo molto blando
in 0 vale 1 e si annulla in 90°; per 0<a<1 non varia sostanzialmente di molto la forma:
siete bravissimi...
ma se lo schermo si muove rispetto all'ombra con velocità relativistica allora mi aspetto che gli eventi diano diversi se visti dallo schermo oppure visti da un osservatore solidale col terreno. C'è qualcosa che non mi torna.
Scusa Leandro, in attesa che domani risponda Enzo, per come descritto, a me sembra che nel quiz non c'è un osservatore sullo schermo in movimento, c'è un osservatore in B che misura la velocità dello schermo (o se preferisci uno in B e uno in B') ed uno in C (o se preferisci uno in C e uno in C') che misura la velocità dell'ombra.
I due osservatori non si muovono uno rispetto all'altro (il loro sistema di riferimento è lo stesso) ed i loro orologi sono sincronizzati.. dal loro punto di vista gli osservatori sono fermi, a muoversi sono lo schermo e l'ombra...
Paolo
Provo a dire la mia.
Se in un istante t vedo l'ombra finire in x(t), il fotone che inizia la zona non in ombra deve avere lambito la saracinesca ad un istante t-x(t)/(c cos(theta)) per arrivare in x(t) all'istante t.
All'istante t-x(t)/(c cos(theta)) la saracinesca arrivava a {y0-vs [t-x(t)/(c cos(theta))]}.
Quindi la relazione che lega x(t) a vs e theta dovrebbe essere
x(t)={y0-vs [t-x(t)/(c cos(theta))]} cot(theta)
che risolta in x(t) diventa
x(t)=(y0-vs t) cot(theta)/{1-vs/[c sin(theta)]}
La velocità dell'ombra è la derivata rispetto al tempo di x(t), che in unità relativistiche è
vo=- (vs/c) cot(theta)/{1-vs/[c sin(theta)]}=- a cos(theta)/(sin(theta)-a)
Per vs>c sin(theta) l'ombra si allungherebbe quando la saracinesca si abbassa e si accorcerebbe quando la saracinesca si alza.
Un altro modo è quello di seguire i percorsi della cima della saracinesca e dei fotoni che la lambiscono.
Se in t1 la saracinesca si trova in y1, il fotone che la lambisce arriverà in x1=y1 cot(theta) all'istante T1=t1+y1/(c sin(theta)).
A t1+d la saracinesca sarà in y1-vs d, il fotone che la lambisce arriverà in x2=[y1-vs d] cot(theta) all'istante T2=t1+d+[y1-vs d]/[c sin(theta)].
La velocità dell'ombra sarà
vo=(x2-x1)/(T2-T1)=- vs cot(theta)/{1-vs/[c sin(theta)] come sopra
Fabrizio
caro Leandro,
come dice Paolo, siamo in un solo sistema di riferimento in cui avvengono i due moti (non confondiamoci con lo spazio-tempo, in cui lo spazio era limitato a una retta). Le attese per l'arrivo o per la scomparsa della luce sono quelle che sono. Non vi è nessun sistema che si muove rispetto a un altro. I movimenti avvengono nello stesso sistema. In fondo, il tempo diverso di arrivo coinvolge già la relatività, in quanto tiene conto di una velocità finita della luce. Non confondiamo sistemi in movimento con movimenti in un sistema.
Volevo fare una osservazione fuori tempo massimo; ho riflettuto parecchio sul fatto che la formula:
(sempre ammesso che sia giusta)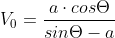 diverge a infinito per
diverge a infinito per ) ; ma che senso ha dire che la velocità è infinita per quel valore di a? O che la velocità diventa negativa?
; ma che senso ha dire che la velocità è infinita per quel valore di a? O che la velocità diventa negativa?
Ho fissato un valore, per esempio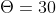 , il denominatore diverge a infinito per a=1/2, e la frazione diventa negativa per a>1/2; ma per me non ha senso applicare quella formula per a>=1/2 (in generale per
, il denominatore diverge a infinito per a=1/2, e la frazione diventa negativa per a>1/2; ma per me non ha senso applicare quella formula per a>=1/2 (in generale per ) );
);
infatti per quei valori di a (velocità saracinesca) l'ombra non si forma mai, quindi non si può parlare di velocità dell'ombra; i raggi che vengono liberati successivamente con quelle velocità di caduta percorrendo spazi più brevi illuminano le zone che dovrebbero essere in ombra. Spero non aver fatto troppa confusione, però in tal caso a resterebbe sempre <1 (quando ci si avvicina a 90)
In realtà, ha senso far variare la velocità in funzione di a per determinati valori di teta, compresi tra o e 90°...
caro Umberto,
ho capito cosa intendi dire... Secondo me l'ombra inizia a viaggiare in senso inverso, da sinistra verso destra. Intendiamo come ombra l'inizio della parte luminosa e l'arretramento del limite dell'ombra....
Avevo gli stessi dubbi di Umberto sul significato di una velocità infinita o negativa dell'ombra.
La cosa mi è sembrata più chiara quando ho pensato a come viaggiano i fronti dei raggi di luce che la saracinesca abbassandosi lascia passare.
Ho cercato di mettere i tre casi,\;&space;\;&space;a>sin(\theta)\;&space;\;&space;e&space;\:&space;\:&space;a=sin(\theta)) in tre figure
in tre figure
dove fisso l'immagine al momento nel quale la saracinesca è ad una certa altezza s. La linea blu è il fronte dei raggi lasciati passare dall'abbassamento della saracinesca.
I raggi lasciati passare per primi hanno raggiunto il pavimento e quindi ridotto l'ombra. Più si abbassa la saracinesca è più si riduce la zona d'ombra a partire da destra.
Se invece) i raggi rimangono indietro rispetto alla saracinesca poiché
i raggi rimangono indietro rispetto alla saracinesca poiché ) , cioé la componente verticale della velocità dei raggi è inferiore a quella della saracinesca
, cioé la componente verticale della velocità dei raggi è inferiore a quella della saracinesca
In questo caso, i raggi lasciati passare dall'abbassamento della saracinesca non raggiungono il pavimento fino a che la saracinesca non è completamente abbassata. A questo punto il pavimento inizia ad essere illuminato a partire da sinistra, sono i raggi lasciati passare per ultimi che arrivano prima al pavimento.
Anche in questo caso l'ombra si riduce, ma a partire da sinistra. Quindi, il segno opposto della velocità non è come pensavo il film al contrario del caso precedente.
Infine, se) il fronte dei raggi rimane all'altezza della saracinesca.
il fronte dei raggi rimane all'altezza della saracinesca.
Quando la saracinesca arriva ad aprirsi totalmente "istantaneamente" il pavimento s'illumina. Cosa che mi sembra dia un senso alla velocità tendente all'infinito del limite dell'ombra.
L'equazione del fronte dei raggi credo sia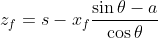 , dove
, dove 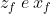 sono rispettivamente la coordinata verticale e quella orizzontale dei punti del fronte. La zona illuminata è quella con
sono rispettivamente la coordinata verticale e quella orizzontale dei punti del fronte. La zona illuminata è quella con 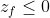 , cioè dove i raggi hanno raggiunto il pavimento.
, cioè dove i raggi hanno raggiunto il pavimento.
Fabrizio
ho paura che si sia mischiato, in generale, un po' troppo la variazione di teta con quella di sin(teta). sin(teta) è costante per ogni esperimento ed è a che cambia fino a raggiungere sin (teta). Il problema dell'inversione del fronte d'ombra è dovuto al fatto che per certi valori di a la luce arriva prima in C' che non in C, e quindi si ha il ramo negativo....
Direi che è ora di descrivere l meglio l'esperimento. Se riesco lo inizio oggi, ma esseno fuori casa non so se ce la faccio... domani sicuramente!
In ogni modo Fabrizio sembra avere colpito nel segno, anche se quella linea blu andrebbe spiegata meglio per i non addetti ai lavori ...
Quante cose si possono fare con un'ombra....
caro Fabrizio,
ho analizzato un po' meglio la situazione e direi che hai proprio utilizzato il metodo migliore per far vedere l'inversione del moto dell'ombra. Cercherò di renderlo ancora più intuitivo, ma il merito è tutto tuo! Complimenti veramente!!!!
Ho cercato di visualizzare in due animazioni gif quanto detto a parole. Spero si riescano a vedere.
Caso)
Caso)
Caso)
Grazie per i complimenti, il merito è da condividere con chi propone i problemi e fa attivare i ragionamenti.
Complimenti. Gran bel lavoro!
caro Fabrizio,
non poso che unirmi a Umberto (che è stato bravo da par suo, come anche altri): lavoro perfetto e ultra esplicativo!!!
Ho avuto contrattempi imprevisti che mi bloccano anche oggi... ritarderò l'uscita della spiegazione dettagliata, di cui voi non avete ovviamente bisogno. Abbiate pazienza... E se riesco inserisco l'ottimo filmato di Fabrizio!!!
Grazie Umberto e grazie ancora Vincenzo.
Adesso divento rosso
Se servisse qualche adattamento alle animazioni per inserirle nella spiegazione sono a disposizione.
Ho notato solo che le gif animate devono essere inserite negli articoli con la dimensione originale, altrimenti sono staticheNei commenti invece sembra di no
Molto belle le animazioni di Fabrizio... complimenti!
Umberto, confermo, negli articoli le gif animate se non imposti "dimensione reale" non partono..
Una sola piccola considerazione sulla funzione trovata: Vo = a cos ϑ/(sinϑ -a).
Vo tende a infinito quando il denominatore tende a zero.
Guardando la funzione si nota subito che la condizione sinϑ= -a individua proprio l'asintoto verticale (qui) a cui tendono i due rami dell'iperbole (quando x tende ad un certo valore finito la y tende a infinito, ossia la curva va verso infinito)....e dato che il limite tendente a zero del denominatore si può raggiungere da sinistra o da destra si passa da -∞ a +∞...
L'asintoto verticale, come mostrano i grafici che ho postato in precedenza, esiste sia se si pone sull'ascissa il valore di ϑ (x=ϑ), sia se si pone il valore di a (x=a)... ovviamente sulle ordinate si trova il valore di V0 (y =V0).
Paolo
carissimi,
ormai siete padroni delle ... ombre!!! Purtroppo, non riesco ad avere tempo per scrivere l'articolo definitivo (in cui userò sicuramente l'animazione di Fabry). Problemi di salute di Barbara, che dovrebbero risolversi entro oggi (spero!). Il quiz, chiamiamolo così, è stato affrontato con grande sapienza e intuito. E' un problemino non banale, che servirà sicuramente per tutti coloro che vogliono cercare di andare a fondo di cose apparentemente inutili, ma che tali non sono: la mente ha fame di questi ragionamenti e di queste considerazioni!
Vi ringrazio tutti per la partecipazione, la volontà e l'impegno. Una vera collaborazione tra persone che vogliono ancora usare il cervello! Vi ringrazio di cuore!!!!
Vi prometto che scriverò un articolo che possa servire a tutti per comprendere appieno la situazione. E voi ne siete stati partecipi attivi e fondamentali. Malgrado gli intoppi, il Circolo va avanti benissimo, grazie a voi...
Ho seguito sin dall'inizio gli sviluppi di questo quiz e mi unisco agli apprezzamenti per il modo in cui è stato ad esso risposto da Fabrizio, Umberto, Paolo e tutti gli altri. Devo dire, però, che continua ancora a ronzarmi in testa la domanda che mi sono fatto sin da quando ho letto la prima volta il quiz: ma, fisicamente, davvero l'ombra può andare più veloce della luce ? Cioè, l'ombra è l'assenza di luce, assenza di fotoni. In che senso un'assenza di fotoni può andare più veloce dei fotoni ?! La risposta più sensata che sinora mi sono dato è che ciò che può muoversi a velocità uguali o anche maggiori a quella della luce è si l'ombra ma senza intenderla come un oggetto. Un esempio per me più intuitivo di come l'ombra possa muoversi alla velocità della luce e oltre è quello di una sorgente di luce (una lampadina ?) al centro di una stanza con le pareti cilindriche e un oggetto che le gira attorno ad una certa distanza da essa. Tale oggetto proietterà la propria ombra sulle pareti della stanza e la velocità con cui l'ombra si muoverà sulle pareti sarà , rispetto a quella con cui l'oggetto ruota attorno alla lampadina, tanto maggiore quanto maggiore è la distanza delle pareti dalla sorgente di luce. In teoria, fissata la velocità angolare di rotazione , sarebbe possibile stabilire una distanza delle pareti tale che la velocità dell'ombra proiettata su di esse sia pari a c ! Ma se, per esempio, tale distanza fosse ... astronomica, la luce, quindi anche la sua assenza quando l'oggetto è davanti alla sorgente, impiegherebbe il suo tempo per arrivare all'osservatore. Caro Enzo, magari oltre alla soluzione dettagliata del quiz, almeno per me penso sarebbe bene approfondire anche questo aspetto, perché io resti convinto che Einstein non sbagliava a proposito del limite della velocità della luce.
caro Arturo,
il tuo dubbio è più che legittimo e ne parleremo nel testo che sto scrivendo (un po' a rilento per vari motivi di famiglia). In realtà l'ombra che si muove non è altro che la luce che arriva, ma che deve compiere percorsi diversi. Questo gioco di ritardi e di anticipi permette di assistere a fenomeni che appaiono più veloci della luce. Ricordiamo sempre, comunque, che l'informazione che giunge alla fine NON supera mai c... E questo è quello che conta.
Grazie Enzo. In effetti , se non fosse come hai scritto, circa l'informazione, ipotizzando di avere sorgenti di luce così potenti da proiettare ombre di lunghezza astronomica, avremmo inventato da tempo un sistema di comunicazione molto più efficiente di quello che utilizza le onde radio...
E sarebbe proprio quello che ho utilizzato per far viaggiare Paolo nel Cosmo con i suoi antifotoni (QUI)

In effetti se sostituiamo l'ombra proiettata con un flusso fotonico laser molto collimato (fisicamente non possibile a causa della diffrazione) che ruota come un annaffiatore in un prato vedremmo che la luce o acqua mentre si allontana dall' irrigatore sembra piegarsi in forma di spirale e non arriva diritta a destinazione. L'ombra sarebbe più veloce di c solo se c fosse più elevata di c.
Volevo solo far notare che il comportamento dell'ombra è molto diverso se questa si sta formando (lo schermo si alza) oppure se si sta ritirando (schermo che si abbassa).
Nel primo caso la velocità dell'ombra è inferiore rispetto a quella dello schermo che si alza (e quindi è inferiore a C), nel secondo caso l'ombra può ritirarsi da destra (velocità positiva) o da sinistra (velocità negativa) a velocità superiori a C che tendono a ± ∞ quando sinϑ = -a.
A mio avviso non è un caso..
Quando si forma l'ombra, l'informazione che si è frapposto un ostacolo che impedisce ai fotoni di raggiungerci viaggia a velocità inferiore a C (a parte il caso limite in cui l'angolo ϑ è uguale a zero e l'ombra viaggia a velocità C).
Quando l'ostacolo si ritira a una certa velocità, è proprio la velocità finita della luce ed il tempo che impiega per raggiungerci a determinare la rapidità (ed il verso) con cui l'ombra si ritira, velocità che può superare in alcune situazioni quella della luce... fino a tendere a infinito (l'ombra scompare istantaneamente).
Oppure il gioco è tra fotoni e antifotoni... mah...
Paolo