Questo articolo non contiene praticamente formule, ma è decisamente FONDAMENTALE per capire l’essenza più profonda della RG e della sua definizione di spazio tridimensionale curvo. Non perdetelo e non esitate a porre domande se vi rimane qualche dubbio. Capirete anche perché abbiamo perso tanto tempo a spiegare le regole geometriche di una superficie sferica (QUI), confrontandole con quelle euclidee e anche perché abbiamo scaldato un piano con una strana piastra (QUI). Sembrerà una trattazione addirittura pedante, ma il concetto di curvatura è troppo importante per rischiare di non chiarirlo completamente.

Prima di cominciare è necessario capire un concetto veramente base. Quando abbiamo detto che viviamo in un mondo, la Terra, che non è euclideo, ci siamo limitati alla superficie sferica della Terra, ossia a una curvatura bidimensionale. Adesso faremo un  passo decisamente più importante e decisivo, cercando di valutare se lo spazio a tre dimensioni che contiene la Terra è uno spazio curvo oppure no. Non andate avanti se non avete capito questo punto. Chiedete senza paura e cercheremo di spiegarlo ancora meglio. Tralasciandone una giusta comprensione, tutta la RG diventerebbe un ostacolo insormontabile e privo di senso…

Abbiamo visto che una superficie curva può essere simulata perfettamente da un piano con una strana piastra che scalda sempre di più allontanandosi dal suo centro. Il calore deforma il righello che serve per misurare le distanze e se viviamo su quel piano la linea di minima distanza è una curva e non una retta. In qualche modo, abbiamo capito che il concetto di curvatura non è essenzialmente dovuto a una superficie realmente “curva” (come la intendiamo noi) ma a un comportamento ben più generale.

Capito questo concetto, possiamo tornare a disegnare una superficie curva attraverso una sfera, dato che le sue stranezze sono molto più semplici da raffigurare. Tuttavia, non dimentichiamoci che è solo un modo comodo per rappresentare la situazione che potrebbe anche essere ottenuta su un piano perfetto, attraverso altre manipolazioni. Piastra che scalda e superficie curva si comportano nello stesso identico modo.

L’importante è che la situazione sia comprensibile da un personaggio che vive nello spazio e ha anch’esso le stesse dimensioni del suo spazio e non attraverso una visione che sfrutta una dimensione supplementare. In altre parole stiamo parlando di curvature intrinseche e non estrinseche. D’altra parte, se questo “furbo” espediente può essere risolutivo per uno spazio a due dimensioni, diventa impraticabile per uno spazio a tre dimensioni (vi sfido a guardarlo in uno spazio con una dimensione in più!). Dobbiamo, perciò, abituarci ad accorgerci di  una “curvatura”del proprio spazio, senza sperare di vederla in modo estrinseco.

Un compito non certo facile, soprattutto da un punto di vista concettuale e intuitivo. Bisogna munirsi di grande immaginazione e riuscire a non essere troppo influenzati dall’aspetto grafico.

Qual è il problema più grande? Sicuramente la confusione che si fa tra sfera sulla cui superficie si disegna uno spazio curvo a due dimensioni e lo spazio a tre dimensioni, contenente una sfera di una certa massa, di cui si vuole misurare o, almeno, scoprire l’eventuale curvatura. In altre parole, lo spazio in cui sta una sfera può essere curvo oppure no, ma di certo non lo indica la forma della sfera che è parte integrante dello spazio. Siamo in balia della visione intrinseca senza nessun aiuto da parte di utili spostamenti in una quarta dimensione.

La forma sferica viene spesso usata solo perché è una figura simmetrica attraverso cui si può determinare la curvatura media dello spazio di cui fa parte. Se poi i pianeti o le stelle sono proprio sfere… tanto meglio!

Stiamo parlando di curvatura che può essere determinata attraverso misure eseguite solo localmente. Questo è quello che Einstein intende per spazio curvo. Ciò che si deve riuscire a fare è, quindi, rendersi conto che, almeno localmente, lo spazio in cui viviamo è curvo. Sarà poi fondamentale capire la causa di tutto ciò… Per colpa di una piastra che allunga i righelli nelle tre dimensioni o per colpa di ciò che definiamo massa (e, quindi, energia)?

Un altro punto importantissimo è che il personaggio che deve risolvere la questione deve essere intelligente e deve avere studiato molto. Lui conosce perfettamente le regole di Euclide e sa, quindi, riconoscere subito se vi è curvatura del suo spazio oppure no.

Facciamo ancora un paio di esempi nelle due dimensioni e poi affrontiamo con cautela le tre dimensioni…

Immaginiamo il nostro studente della volta scorsa (QUI), che su una superficie estrinsecamente curva o riscaldata in qualche modo, voglia muoversi per ottenere un quadrato. Parte da un punto e segue tratti di uguale distanza (per lui) piegando al momento giusto di 90°. Per quanto detto precedentemente (e lo potete provare direttamente), in entrambi i casi, alla fine del percorso, non si trova sicuramente nel punto di partenza.

Lui non ha tracciato una figura intrinsecamente curva, dato che ha seguito le regole di Euclide (retta, angolo 90°, retta, angolo 90°,…), tuttavia alla fine il risultato non è conforme a quello previsto. Risultato: si accorge che il suo spazio non è euclideo, ossia è curvo. Ripetiamo: si accorge di vivere in uno spazio curvo dato che una figura che non è curva nel suo mondo dà luogo a un risultato non conforme a quanto previsto da Euclide.

Facciamo un secondo esempio ancora più calzante per il proseguo della trattazione. Lo studente prende una corda e la fissa in punto P qualsiasi (Fig. 1).

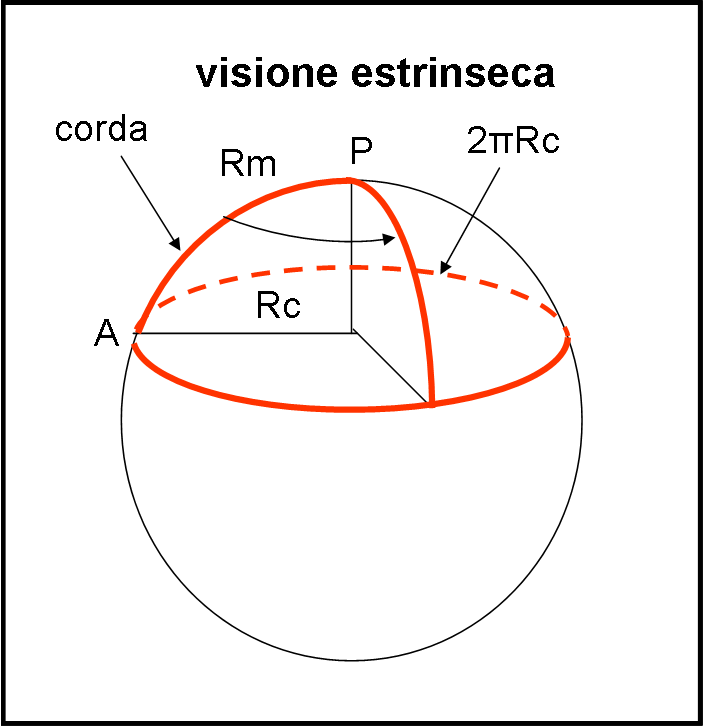
Poi si sposta fino al punto A, in modo che la corda sia ben tesa. In altre parole, ha percorso il tratto, per lui rettilineo, Rm. Comincia a camminare, mantenendo sempre la corda ben tesa. Alla fine si ritroverà nel punto di partenza A (come è capitato al piccolo riccio che abbiamo conosciuto QUI).

Nuovamente, la stessa cosa capita sia sulla superficie sferica che sul piano riscaldato (basta fissare la corda nel centro della piastra). Può concludere che NON è su uno spazio curvo? Assolutamente no. Lui ha solo scoperto di avere descritto una circonferenza di raggio Rm. In altre parole, lui ha effettivamente disegnato una curva intrinseca, che non lo stupisce di certo e non contraddice assolutamente Euclide (anche nel piano una circonferenza si traccia nello stesso identico modo!).

A questo punto, però, oltre che a misurare il raggio Rm (la corda), può anche misurare la circonferenza che ha descritto. La chiama C. Notiamo bene che mentre la circonferenza C può essere misurata direttamente (curva intrinseca), non lo è di certo la distanza Rc che è completamente fuori dallo spazio in cui vive. La vediamo noi perché abbiamo aggiunto una dimensione... Lui può solo calcolarlo utilizzando Euclide.

Infatti, conoscendo Euclide, sa benissimo che il rapporto tra circonferenza e raggio è dato da un numero “fatato”, uguale a circa 6.28… (2π). Non gli rimane che dividere il suo valore di C per 6.28 e dovrebbe aspettarsi di trovare il raggio misurato Rm. Pensate che lo trovi? Nemmeno per sogno. Lui trova un numero più piccolo del suo, Rc (raggio calcolato). In formula matematica:

Rm  > Rc = C/2π

Ossia:

Rm – Rc = dR

Essendo istruito, non si spaventa più di tanto e conclude che il suo mondo a due dimensioni è CURVO, senza preoccuparsi troppo a cosa sia dovuta la curvatura. La sua curva intrinseca (circonferenza) non risponde ai principi di Euclide, dato che il raggio è più lungo del previsto. Non è la circonferenza “curva” che ha tracciato a fargli capire qualcosa, ma le sue caratteristiche confrontate con quelle della geometria euclidea. Tutto chiaro? Se non lo fosse, bloccatemi!

Fino a qui, penso che i problemi concettuali si riescano a inquadrare molto bene attraverso le figure corrispondenti. Figure che utilizzano, però, la terza dimensione. Ci piace vincere facile… Potremmo dire: basta guardare le cose dal di fuori e si vede benissimo che quello strano mondo è curvo, senza bisogno di fare tante misure…

Adesso, dobbiamo fare il passo più difficile: entrare nello spazio a tre dimensioni, in cui diventiamo personaggi obbligati a decidere se esso è euclideo oppure è curvo, vivendo al suo interno e senza nessuna figura con una dimensione in più che ci possa illuminare. Vincere non è più così facile…

La faccenda non è “matematicamente” semplice -anzi- ma a noi basta afferrare il concetto di base.

Innanzitutto, non abbiamo più una direzione particolare in cui introdurre un’eventuale curvatura. Essa può esistere in tutte le direzioni. Mi spiego meglio. Potremmo disegnare un triangolo e guardare se la somma dei suoi angoli è 180°. Oppure disegnare una circonferenza e vedere se il suo raggio è quello che ci si aspetterebbe da una geometria euclidea. O disegnare un quadrato e vedere se si chiude. Staremmo comunque valutando la curvatura in una sola direzione. Cosa succederebbe se il triangolo fosse ruotato o si cambiasse il piano della circonferenza?

La curvatura in tre dimensioni presenta componenti di curvatura che possono essere anche diverse. In parole più semplici, se trovassimo un eccesso di curvatura in una circonferenza, potremmo non trovarla o trovarla completamente diversa, ruotando la nostra circonferenza di 90°.

Soffermiamoci su questo esempio, quello più facile da comprendere. Attenzione al ragionamento da fare, evitando le confusioni con lo spazio a due dimensioni.

Teoricamente, potremmo far girare la circonferenza, variando regolarmente l’angolo tra i due piani, e vedere che curvatura ha di volta in volta. Tuttavia, c’è un metodo più semplice. Perché non considerare una sfera e agire su di lei in modo “globale”?

Innanzitutto, definiamo la sfera in questo spazio a tre dimensioni: essa è il luogo di tutti i punti che abbiano la stessa distanza da un punto detto centro. Attenzione: stiamo facendo la costruzione basandoci sul nostro metodo di misura delle distanze. In modo del tutto analogo a quando abbiamo disegnato una circonferenza su una superficie sferica a due dimensioni con una corda che per noi era la minima distanza.  In quel caso era stato facile vedere la situazione in modo estrinseco.

Questa volta NON possiamo più usare quella verifica e dobbiamo solo fidarci della conoscenza delle regole euclidee.

Dividiamo allora la superficie sferica così costruita (ossia attraverso una corda sempre uguale) in tanti quadratini infinitesimi e sommiamo le loro aree (Fig. 2).

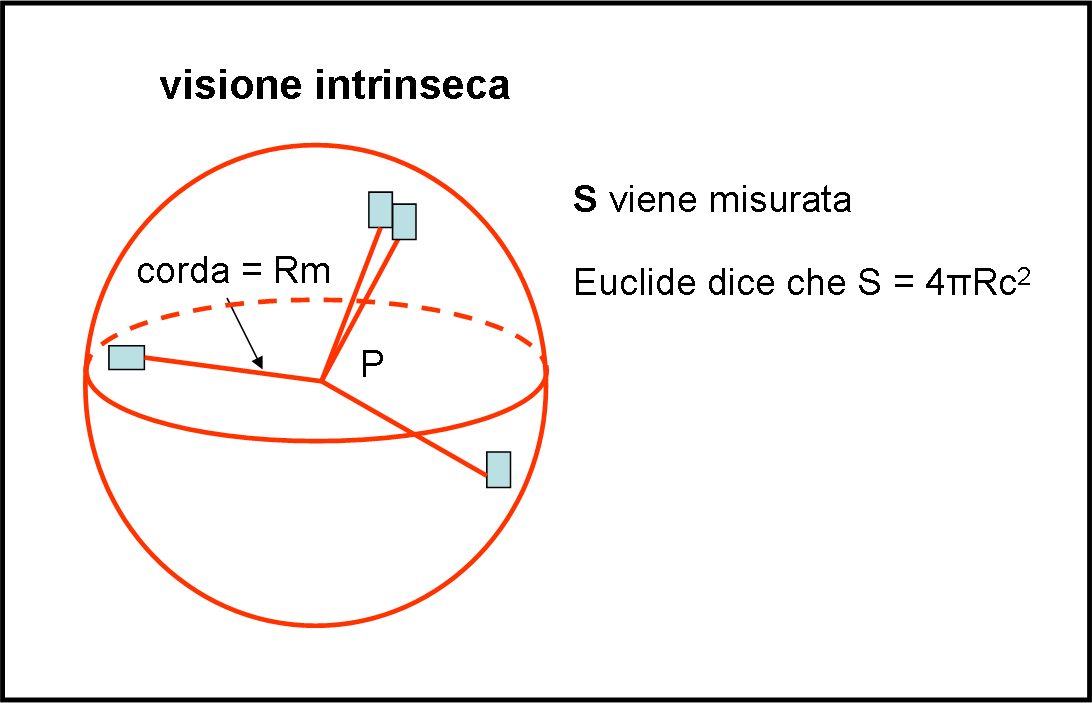
Così come avevamo misurato, precedentemente, la circonferenza costruita con la corda, adesso possiamo misurare la superficie sferica costruita con una corda del tutto simile di lunghezza Rm, libera di muoversi in tutte le direzioni dello spazio a tre dimensioni, dove stiamo vivendo.

Ribadiamo ancora: disegnando la sfera abbiamo disegnato una "curva" intrinseca nello spazio a tre dimensioni, così come avevamo disegnato una circonferenza nello spazio a due dimensioni. Non è la sfera a dirci se lo spazio è curvo, così come non era la circonferenza a dirci se lo spazio bidimensionale era curvo. Tutti d’accoro? Bene, allora possiamo proseguire…

Noi siamo istruiti e sappiamo perfettamente che Euclide dice che la superficie sferica è data da S = 4πR². Ne segue che possiamo facilmente determinare il raggio previsto da Euclide:

Rc = (S/4π)^1/2

Non ci resta che confrontare questo raggio con quello misurato, che ci è servito a costruire la sfera. Se troviamo un eccesso di raggio dR, ossia se:

Rm – Rc = dR

possiamo VERAMENTE concludere che viviamo in uno spazio tridimensionale curvo.

Ribadiamo ancora la differenza fondamentale tra i sue spazi. Nel primo, a due dimensioni, che avevamo rappresentato (vedendolo dalla terza dimensione) come una superficie sferica o come un piano riscaldato da una piastra, avevamo disegnato una circonferenza; nel secondo, che non possiamo rappresentare estrinsecamente, abbiamo disegnato una sfera. Il confronto va fatto tra la circonferenza e la sfera intese come entità geometriche intrinsecamente curve, relative a due spazi di dimensioni diverse.

Qualsiasi sia il raggio della sfera, così come qualsiasi sia il raggio della circonferenza, il problema della curvatura è esattamente la stesso. Ciò che conta è la differenza, se esiste, tra il raggio calcolato a partire dalla superficie sferica (calcolato SOLO attraverso Euclide) o dalla circonferenza (calcolato attraverso Euclide o attraverso una figura con una dimensione in più) e il raggio misurato nello spazio in cui si vive, ossia la corda usata per la costruzione della figura.

A costo di essere pedante: la curvatura dello spazio a tre dimensioni, contenente una sfera, non dipende assolutamente dal raggio della sfera, ma dal confronto tra raggio misurato direttamente e raggio calcolato con Euclide.

Tutto chiaro? Bene, anzi benissimo. Anche se non sembra, abbiamo fatto un gran bel lavoro e il concetto reale di curvatura di uno spazio non ha più problemi.

Tuttavia, matematicamente, siamo ancora lontani da una definizione accurata di spazio curvo. Noi, infatti, abbiamo trovato una curvatura MEDIA. Conoscendo solo l’eccesso medio abbiamo solo una vaga idea della effettiva curvatura di una parte del nostro spazio, ossia di quella in cui è contenuta la sfera.

Ribadiamo ancora: la circonferenza bidimensionale descriveva una parte dell’intero spazio bidimensionale, in modo perfetto. La sfera, di cui abbiamo determinato la curvatura media nelle tre dimensioni, ci indica, molto rozzamente, la curvatura di una piccola parte dell’intero spazio tridimensionale.

Diciamo subito che, per definire accuratamente la vera curvatura locale, sarebbero necessari ben sei parametri di curvatura. E già possiamo capire perché le formule finali della Relatività Generale diventano piuttosto complicate: sei numeri per ogni curvatura locale e le varie formule che li legano ad altre grandezze.  Per adesso (e per noi), la curvatura media basta e avanza…

La grande domanda che vogliamo farci, pur con le sue limitazioni, è: “Siamo in grado di dire se il nostro spazio è mediamente curvo oppure no?”. La risposta è SI e il risultato ricorda forse molto di più il caso della piastra che non quello di una superficie sferica. Non ve l’aspettavate, vero? E, invece, tra poco, concorderete con me…

Purtroppo, una misura della Terra, intesa come spazio tridimensionale, sembrerebbe portare a un risultato negativo, ma la faccenda non deve stupire se affrontiamo di petto il motivo di uno spazio tridimensionale curvo. Le misure non sono abbastanza accurate per valutare un eventuale “eccesso” nel raggio.

E qui entra in ballo Einstein che, attraverso la sua teoria, ci permette di capire perché è così difficile calcolare la curvatura dovuta alla Terra. Facendo conti piuttosto impegnativi è stato in grado di dire che lo spazio è curvo, ma che la Terra è un’attrice di scarso rilievo, una comparsa....

Il succo del discorso è questo: se esiste un luogo dello spazio che contiene una massa M e noi immaginiamo di concentrala in una sfera così piccola (e densa) tale da poter ammettere che la sua densità si possa considerare costante, allora esiste un eccesso di raggio dR che può essere scritto come:

dR= Rm – Rc = Rm – (S/4π)^1/2 = (G/3c²)M

Risulta immediatamente chiaro che l’unica variabile è la massa contenuta all’interno (il resto è una costante). La formula precedente viene detta la legge di Einstein per la curvatura media dello spazio tridimensionale. Notiamo subito che nella costante compare la velocità della luce e la costante di gravitazione. Il “profumo” è già quello di un cambiamento epocale…

Passiamo subito a un caso pratico, inserendo i valori conosciuti per le costanti G e c e per la massa della Terra (considerata di densità costante). Otteniamo:

dR(Terra) = 1.5 mm

Una cosa ridicola (ecco perché sarebbe impossibile calcolarlo direttamente), ma tale da poter dire che lo spazio tridimensionale in cui viviamo localmente è curvo per effetto della sola massa della Terra.

E se facessimo la stessa cosa per il Sole? Beh… il risultato sarebbe più significativo, anche se sempre minimo:

dR(Sole) = 0.5 km

E’ chiaro che, per sentirsi realmente preda di uno spazio “curvo” , sono necessarie masse ben più grandi. E più la massa viene compressa in un volume piccolo (ossia aumentando la densità) è maggiore è l’effetto locale, potendo arrivare più vicino alla zona “critica”.

Già capiamo però che, allontanandosi dalle masse, la trattazione assomiglia sempre più al caso trattato nella Relatività Ristretta. Ancora una volta possiamo dire che la Relatività Generale diventa fondamentale in punti particolari dello spazio, dove esistono masse significative, altrimenti Minkowski è più che sufficiente. La Relatività Ristretta è chiaramente un caso particolare (anche se molto comune) della Relatività Generale.

E’ abbastanza ovvio interpretare il risultato ottenuto precedentemente, grazie al genio di Einstein, come estremamente simile a quello della piastra… La piastra tridimensionale diventa la massa e più vicino si riesce ad arrivare più il regolo cambia di lunghezza. In parole povere, le masse riescono a cambiare l’unità di misura dello spazio, a mano a mano che ci avviciniamo a loro.

L’effetto che si riscontra è del tutto simile a quello di uno spazio curvo e la massa prende il significato di “motore” capace di rendere non euclideo lo spazio circostante. Le traiettorie di minimo percorso non sono più intrinsecamente rette euclidee, ma archi di curva e via dicendo. Curve che non sono visibili estrinsecamente (non possiamo, infatti, aggiungere una dimensione), ma che si “scoprono” confrontando la geometria spaziale con quella euclidea.

Attenzione, però… si potrebbe anche continuare in questa trattazione relativamente semplice, ma ci saremmo dimenticati di un dato di fatto fondamentale che Newton non aveva considerato: lo spazio e il tempo sono profondamente legati (le trasformazioni di Lorentz insegnano …) e, quindi, questo gioco di deformazione spaziale è costretta a diventare una deformazione spazio-temporale, con tutte le complicazioni del caso.

Non è ancora ora di occuparci del tempo e limitiamoci a pensare al fatto che se considerassimo uno spazio sufficientemente grande, al suo interno sarebbero sicuramente collocate delle masse di tutte le dimensioni. Al di là del loro effetto locale, l’insieme di tutte queste masse, inserite un po’ casualmente, ma con una certa regolarità, potrebbe dar luogo a uno spazio generale (ossia che le contenga tutte) curvo? Tante piccole piastre possono creare una specie di piastra unica su grande scala?

Per rispondere in modo “osservativo”, l’ideale sarebbe poter prendere una sfera enorme (ricordiamoci che prendiamo una sfera perché ci regala un modo semplice per valutare la sua eventuale curvatura spaziale), composta da galassie poste alla stessa distanza e cercare di confrontare la distanza misurata e quella prevista, utilizzando le regole euclidee, così come abbiamo fatto per la Terra.

In questo modo, potremmo sapere se lo spazio nel suo insieme (potremmo già chiamarlo un pezzo significativo di Universo ), in cui sono contenute masse in modo più o meno omogeneo, sia uno spazio euclideo oppure curvo. In altre parole, piatto oppure no. Come vediamo molto bene ci avviciniamo a quella che viene chiamata “forma” dell’Universo (della quale abbiamo parlato QUI).

Molti sono stati i tentativi in tal senso, ma la risposta è ancora molto aleatoria, anche se si pensa sempre di più a uno spazio piatto (quello teoricamente più probabile, oltre che avvalorato da osservazioni indirette), che non lede comunque la curvatura locale nei pressi di ogni singola massa.

Bene… tanto lavoro per nulla (o quasi…)? No, di certo… Siamo sicuramente pronti per capire cosa significhi realmente uno spazio curvo e, in particolare, uno spazio localmente curvo. Tuttavia, la Relatività Ristretta ci ammonisce di non essere troppo contenti. Abbiamo fatto solo un piccolo passo. Qualsiasi cosa faccia lo spazio non può non influire sul suo fratello gemello, il tempo. Ed è così che le equazioni di Einstein diventano molto meno semplici, ma permettono di costruire un regola che sembra più indistruttibile della stessa realtà delle cose. Lo spazio si lega al tempo e alle masse (ossia all’energia) è la faccenda diventa entusiasmante.

Alla prossima… ricordando che, pur nella sua limitatezza, questo articolo è di importanza fondamentale e che qualsiasi dubbio a riguardo deve essere chiarito senza alcun timore… mi raccomando!

 

Questo articolo fa parte della serie "Verso la RG", in quanto propedeutico alla comprensione della Relatività Generale, QUI trovate tutti quelli che sono stati scritti fino ad ora.

QUI trovate l'approfondimento dedicato alla Relatività Generale