Questa è una soluzione approssimata, a cui sono giunto per via grafica, al quiz della volpe e del coniglio (che trovate QUI), alternativa a quella proposta da Vincenzo (che trovate QUI).

Prima che venga dato il via alla caccia, la volpe e il coniglio sono fermi, distanziati tra loro di una certa lunghezza che indichiamo con d.

All’istante t=0, la volpe, visto il coniglio, inizia a correre verso di lui con velocità di modulo pari a v. Il coniglio, avvertito il pericolo, si mette a correre istantaneamente, quindi allo stesso t=0, ad una velocità anche essa di modulo pari a v ma con direzione inclinata di un certo angolo  rispetto alla direzione della volpe. Nel mio modello grafico ho posto  = 90 gradi, ma potrebbe essere un qualsiasi angolo compreso tra 0 e 180 gradi.

Dopo una frazione di tempo dt dall’inizio della corsa del coniglio, quindi all’istante t=0+dt,  la volpe, vedendo che questo si è spostato un po’ verso destra, corregge la direzione della propria corsa e punta nuovamente verso il coniglio. Ma quest’ultimo se ne accorge istantaneamente e devia nuovamente di un angolo  la direzione della propria fuga, rispetto alla direzione della volpe.

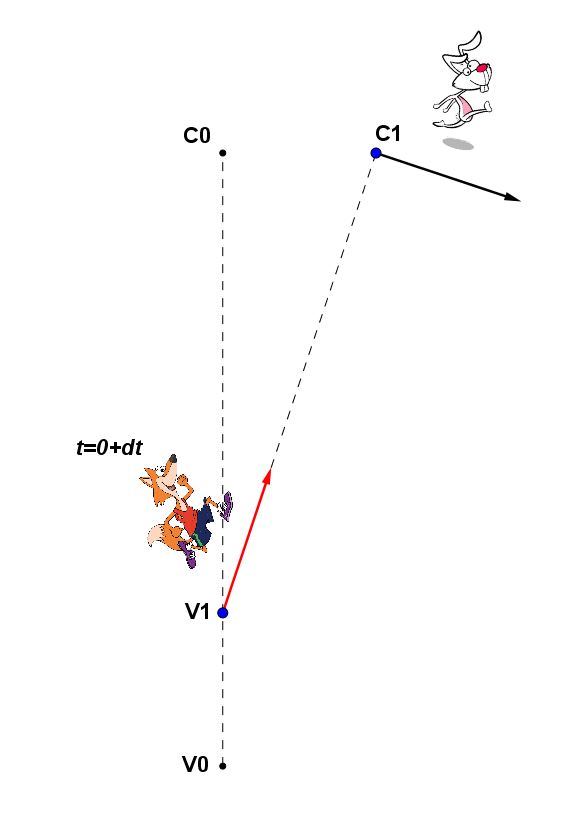
Dopo un ulteriore frazione di tempo dt, quindi all’istante t=0+dt+dt, la volpe ripunta verso il coniglio e questo devia nuovamente dell’angolo :

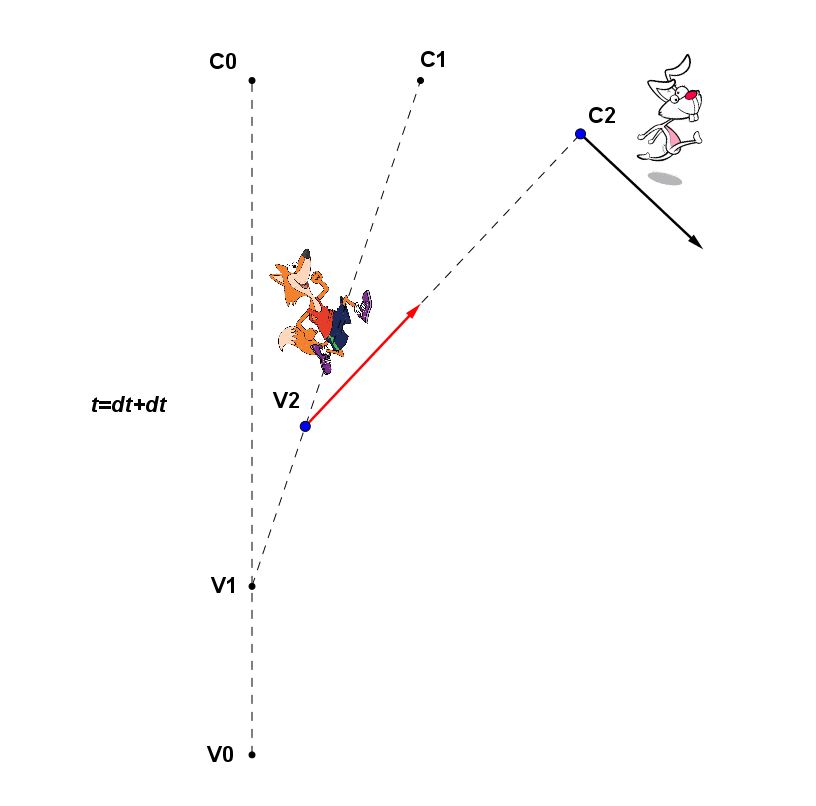
Ho continuato a reiterare questo evento per vedere come andava a finire. Così, dopo qualche tentativo ho capito che con dt troppo grande (a cui corrispondono tratti elementari ds di traiettoria attraverso la relazione v=ds/dt) sembrava quasi che volpe e coniglio, pur avvicinandosi, dovessero alla fine restare separati indefinitamente di una certa lunghezza, pari proprio a ds. Riducendo l’intervallino dt, invece, si nota che le due traiettorie seguite rispettivamente da volpe e coniglio, vanno a confluire in un punto, chiamato C nelle figure, situato sull’asse del segmento iniziale  e distanziato da questo di d/2. In perfetta sintonia con la soluzione pubblicata da Vincenzo.

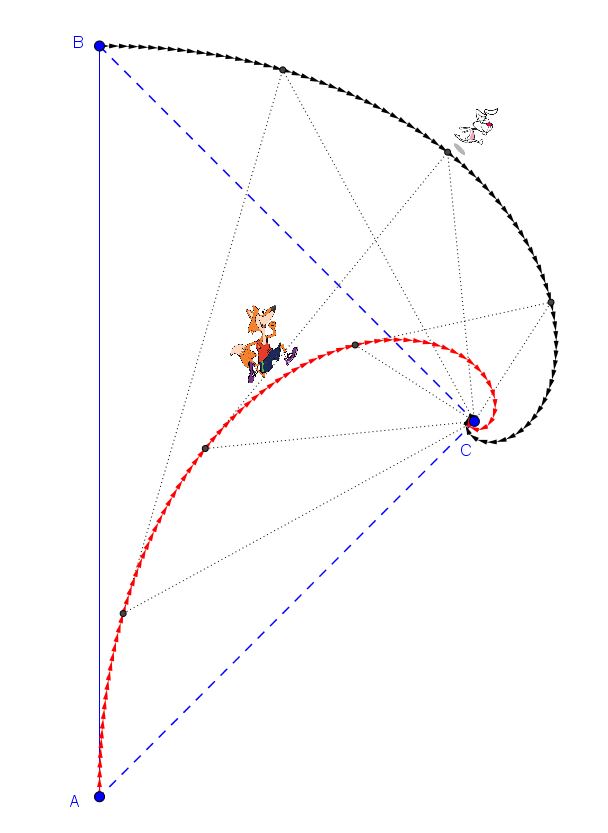
Ma non basta.

Fissato un valore di v pari a 10 m/s, ho impostato il ds in maniera tale da avere un intervallino elementare di tempo dt pari a ds/v = 0,091/10=0,0091 s, cioè poco meno di 1/100 di secondo.  Fissata una distanza d iniziale pari a 7 metri, ho ottenuto il risultato grafico suddetto con un numero di passi pari a 80. Ho potuto a quel punto calcolare il tempo impiegato dalla volpe a raggiungere il coniglio, semplicemente moltiplicando il dt per il numero di passi: 0,0091 x 80 = 0,728 s, in buono accordo con il risultato trovato tramite la formula indicata da Vincenzo [d/v(1-cos alfa)].

Dopo 80 passi, la distanza finale tra volpe e coniglio è risultata pari a 0,091 m, cioè circa 9 cm, mentre la distanza della volpe o del coniglio dal punto C è risultata pari a circa 6 cm. Considerate dimensioni fisiche di una volpe e quelle di un coniglio, che non sono ovviamente quelle puntiformi del modello grafico, possiamo tranquillamente affermare che , anche con l’approssimazione del modello grafico, la volpe riesce a raggiungere il coniglio e lo fa nel punto C.

Inoltre, ho potuto calcolare la lunghezza complessiva della traiettoria percorsa dalla volpe, semplicemente moltiplicando il ds per il numero di passi: 0,091 x 80 = 7,28m. Con quale valore confrontare questo dato ? Mi sono, a questo proposito, chiesto cosa rappresentasse, geometricamente, la traiettoria della volpe (ma le identiche considerazioni possono farsi per quella del coniglio). Dalla successione dei tratti elementari di traiettoria venuta fuori dal procedimento grafico , nonché dalla constatazione che l’angolo tra la direzione del moto del coniglio e quella della congiungente i due animali si mantiene costante, sono giunto alla conclusione che si tratta di una spirale logaritmica. L’equazione generica di una spirale logaritmica in coordinate polari è :

          (1)

dove r è la distanza del generico punto P della spirale dalla sua origine e θ è l’angolo compreso tra la congiungente l’origine della spirale con il generico punto P e l’asse x.

Con riferimento al nostro caso, se la traiettoria della volpe è una spirale logaritmica, essa , per angolo θ = 5/4 π   (225 °)  deve passate per il punto A, cioè deve risultare

Sostituendo i valori nell’equazione (1) e ponendo b=1,  ricavo a:

Inoltre, volendo rappresentarla in coordinate cartesiane attraverso le due equazioni parametriche:

devo tenere conto del fatto che l’origine della spirale non è nell’origine degli assi, ma nel punto C, quindi:

In definitiva, la traiettoria della volpe, se fosse una spirale logaritmica, sarebbe rappresentata dalle equazioni parametriche:

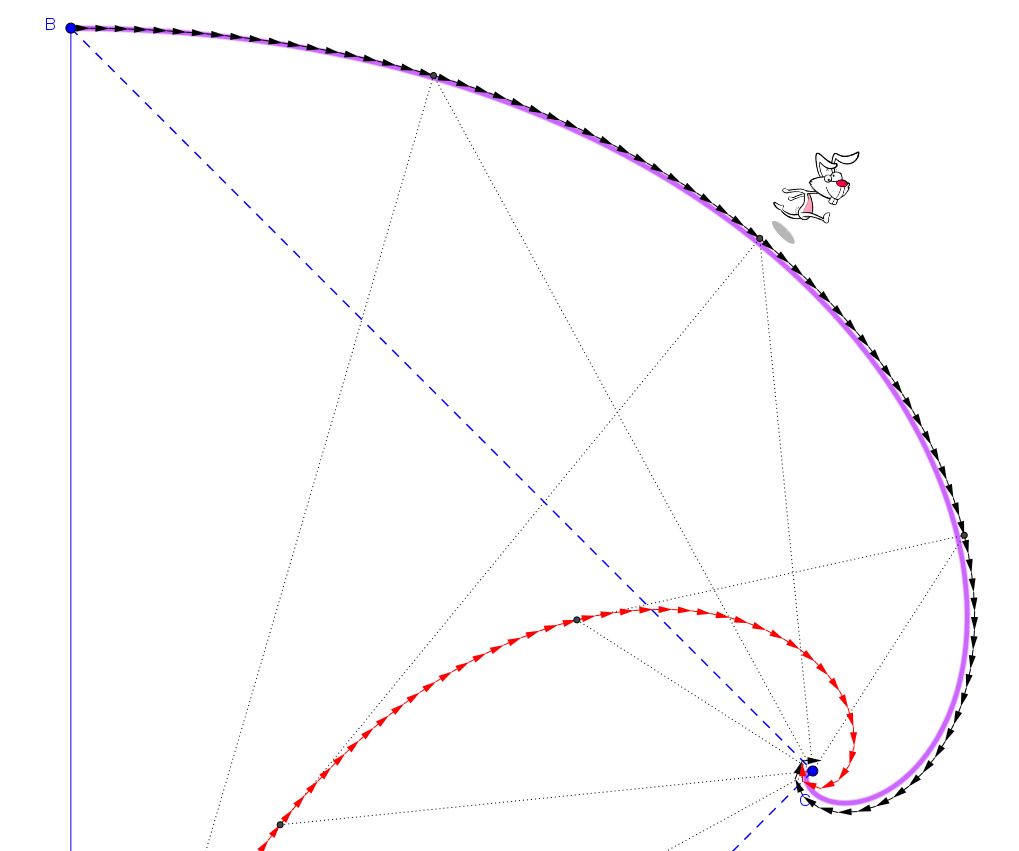
Ebbene, ho tracciato graficamente tale curva ottenendo il seguente risultato. La spirale è la curva verde.

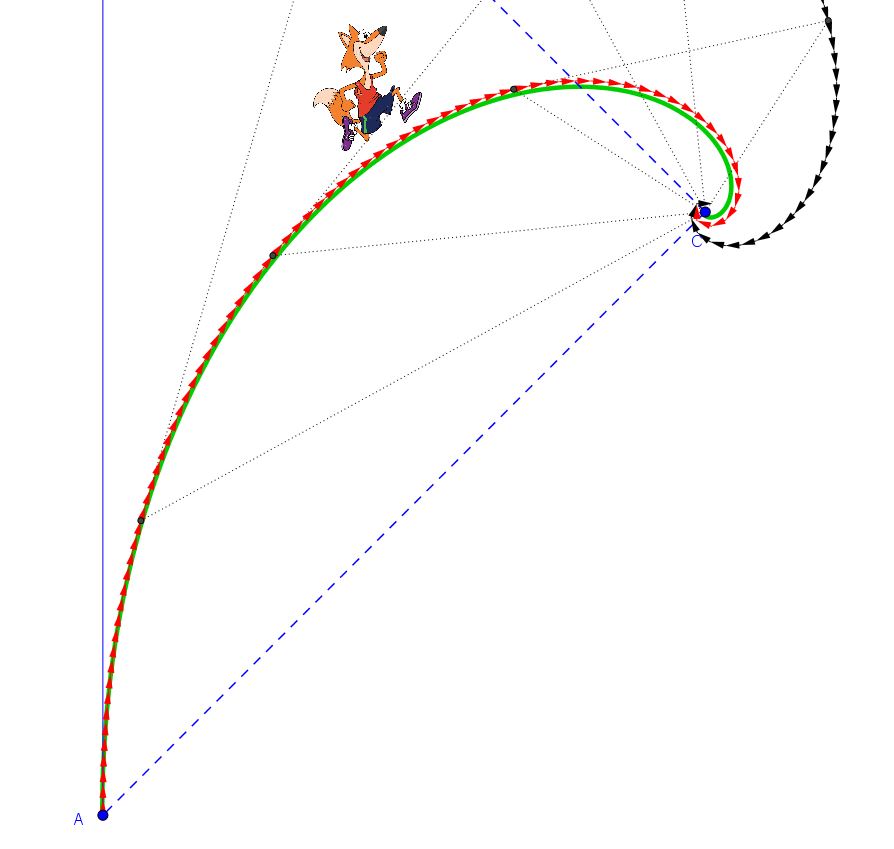
Si nota un’ottima  sovrapponibilità di questa con la traiettoria “discreta” ricavata graficamente. Approssimandoci all’origine della spirale, cioè al punto C, le differenze tra spirale logaritmica e traiettoria discreta diventano un po’ più marcate ma questo dipende dall’entità del dt. Qualora spingessi la discretizzazione della traiettoria a intervalli ancora più piccoli, alla fine quest’ultima sarebbe pressoché identica alla spirale logaritmica sopra ricavata.

E la traiettoria del coniglio ? E’ anche essa una spirale logaritmica, con origine nel punto C e con lo stesso valore del coefficiente a, ma semplicemente ruotata in senso orario di un angolo pari a 90 gradi. In figura è la curva di colore viola.

A questo punto, posso calcolare la lunghezza del percorso seguito ad esempio dalla volpe tramite la formula che deriva dalla teoria della spirale logaritmica:

Nel caso che interessa , vogliamo calcolare l’arco di spirale che va dalla sua origine (punto C) al punto A  (in corrispondenza del quale si ha ). Sostituendo i valori già trovati per a e b, alla fine otteniamo s=d=7 metri.

Confronto ora questo valore con quello che avevo trovato con la soluzione grafica (7,28m) e noto anche in questo caso una buona approssimazione.

In definitiva, la soluzione grafica approssimata da me adottata risulta in buon accordo con quella rigorosa ottenuta da Vincenzo.

(QUI  l'articolo di Vincenzo sulla spirale logaritmica)