Grazie a tutti coloro che hanno manifestato interesse per questo quiz, attestato dall'elevato numero di visite, e a coloro che hanno partecipato con le proprie risposte.

La risposta alla domanda posta dal quiz è affermativa. L'occorrente per far cadere più lentamente il disco cilindrico è già tutto presente e non ci serve altro. Basta solo avvolgere il filo attorno alla superficie laterale del disco cilindrico , portando poi quest'ultimo all'altezza del punto di ancoraggio del filo e lasciandolo cadere in maniera tale che il filo si svolga man mano che il disco cade. Insomma, qualcosa di molto simile ad un gioco con cui molti di noi si saranno almeno una volta divertiti da ragazzi (e anche da grandi): lo yo-yo.

Si osserva in tal modo che il disco cade verticalmente in modo più lento rispetto a quando il filo non è avvolto su di esso. In quel caso, infatti, il disco in caduta semplicemente trasla in direzione verticale, senza ruotare su sè stesso.

Possiamo affrontare analiticamente il problema applicando il principio di conservazione dell'energia meccanica. Abbiamo supposto trascurabili gli attriti e la resistenza del mezzo. Le uniche energie in gioco sono dunque quella cinetica traslazionale , dovuta al fatto che il disco, ad un certo istante t, ha una velocità v(t) diretta verso il basso, l'energia cinetica rotazionale, dovuta al fatto che il disco, all'istante t, ruota , mentre cade, con velocità angolare (t) , e l'energia potenziale gravitazionale, dovuta al fatto che il cilindro , all'istante t, si trova ad una altezza h(t) rispetto al suolo (che assumiamo come piano di riferimento).

Per il principio di conservazione dell'energia deve, dunque, risultare:

               (1)

cioè l'energia meccanica all'istante iniziale deve essere uguale all'energia meccanica al generico istante di tempo t. All'istante iniziale, quando il disco è ancora fermo a quota H dal suolo, abbiamo solo energia potenziale gravitazionale, quindi:

avendo indicato con m la massa del disco cilindrico (quella del filo l'abbiamo supposta trascurabile). All'istante di tempo generico t, invece, il disco è in caduta , quindi ha una velocità di traslazione verso il basso v(t) e una di rotazione attorno al suo asse (t). In particolare, indichiamo con t l'istante di tempo in cui il disco impatta al suolo. In tale istante l'energia potenziale gravitazionale iniziale si sarà completamente convertita in energia cinetica traslazionale e rotazionale. Quindi, nell'istante di impatto, l'energia meccanica sarà data solo da energia cinetica:

avendo indicato con I il momento di inerzia del disco rotante attorno al proprio asse (pari a  , se con R indichiamo il raggio del disco)

Per la (1), dunque , risulta:

           (2)

Inoltre, il filo avvolto al disco, mentre si svolge, non slitta sulla superficie laterale del disco (perché lo avevamo precedentemente ben fissato ad una estremità al disco e lo avevamo ben avvolto attorno ad esso). Vi è dunque una perfetta corrispondenza tra la velocità di traslazione verso il basso del disco e quella di rotazione attorno al suo asse. Si ha, cioè, che:

che , sostituita nella (2) permette di riscriverla come:

cioè, sostituendo ad I la sua espressione:

cioè:

da cui, dividendo tutto per m ed esplicitando rispetto a v:

Se confrontiamo tale espressione con quella nota della velocità   con cui un oggetto in caduta libera da altezza H impatta al suolo , pari a , ci accorgiamo che

        (perché )

In definitiva, il disco che cade avvolto sul filo a cui era sospeso, lo fa più lentamente rispetto alla caduta libera senza alcun filo.

Volendo sapere con quale accelerazione avviene la caduta del disco, basta applicare le leggi orarie del moto uniformemente accelerato, dove, al posto di g ci mettiamo a, incognita del problema.

In particolare , usiamo la legge:

avendo indicato con s lo spazio percorso.

Essendo, nel nostro caso, H lo spazio totale percorso durante il moto uniformemente accelerato con accelerazione a , ed essendo nulla la velocità iniziale v(0) , alla fine otteniamo:

da cui, esplicitando rispetto ad a:

sostituendo ora a v l'espressione prima ottenuta, si ha:

In definitiva, l'accelerazione con cui il disco con il filo avvolto cade verticalmente è pari a 2/3 di quella di gravità.

Ma vediamo un caso pratico. Analizziamolo dapprima in maniera simulata, utilizzando cioè il computer. Abbiamo due dischi identici, stessa massa, stesso diametro, stesso materiale, posti alla stessa altezza H dal suolo (nel modello pari a 12 metri). Al disco di sinistra è avvolto senza lasco il filo inestensibile e di massa trascurabile. Il disco di destra è assolutamente libero. Li lasciamo cadere nello stesso istante. Il video seguente illustra la caduta simulata con il computer:

OK, il filo attorno al disco di sinistra non è avvolto esattamente come nel quiz, ma non si poteva fare di meglio nella fase di modellazione. I grafici sulla destra sono quelli della velocità dei dischi in funzione del tempo. Il grafico superiore è relativo al disco di destra, ossia quello in caduta libera senza filo. Quello inferiore è relativo al disco di sinistra, ossia quello con il filo avvolto.

Naturalmente, la pendenza media dei due grafici non è altro che la derivata della velocità rispetto al tempo, cioè l'accelerazione.

Ingrandiamo tali grafici.

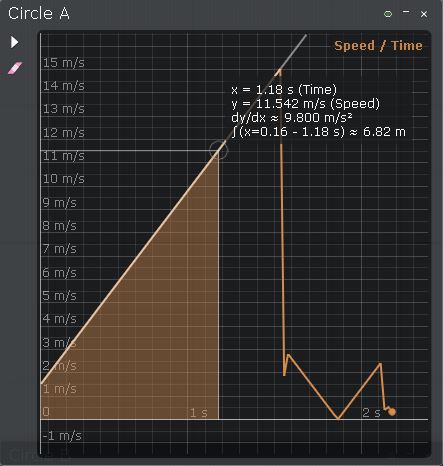
La velocità con cui il disco di destra impatta al suolo è di circa 15 m/s, in ottimo accordo con la teoria. L'accelerazione in questo caso è quella di gravità.

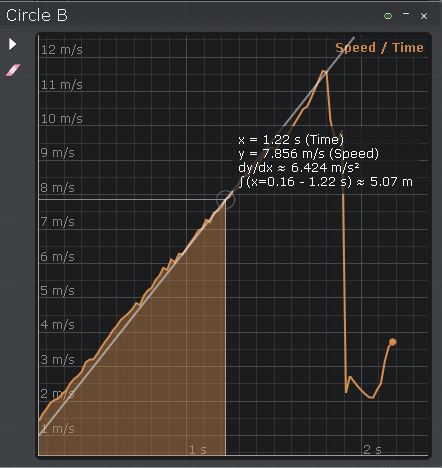
Nel caso del disco con il filo avvolto, invece, la velocità con cui esso impatta al suolo risulta di circa 11,5 m/s, leggermente inferiore a quella attesa in base alla teroia (12,5 m/s), sicuramente per le approssimazioni del modello a proposito del filo avvolto sul disco. L'accelerazione media risulta pari a circa 6,4   , in buon accordo con il valore atteso in base alla teoria (6,54 ).

Ora vi proponiamo, un caso pratico nel vero senso del termine.. 

Due pulegge in alluminio assolutamente identiche, ma una con il solito filo di massa trascurabile e ben avvolto attorno, vengono fatte cadere contemporaneamente da una stessa altezza (circa 2,30 metri) e riprese con una Go-Pro Hero2 impostata a 100 frames/s. Abbiamo rallentato il video così da ottenere un effetto "slow motion". La qualità del risultato non è il massimo, ma crediamo sia sufficiente per i nostri fini.

E' evidente la caduta più lenta del disco a sinistra , quello con il filo avvolto. Il materassino gonfiabile in basso è servito a evitare che l'energia cinetica delle pulegge in caduta si trasferisse nell'urto al pavimento sottostante, con conseguenze imprevedibili sulla tenuta familiare... 

QUI trovate tutti i quiz del Club dei Maghi