Per una trattazione completa dell'entrata nel buco nero, si consiglia di leggere il relativo approfondimento, nel quale è stato inserito anche il presente articolo.

 

E' arrivato il momento di introdurre il diagramma di Penrose, che ci accompagnerà, con relativa semplicità, a scoprire i segreti racchiusi dentro l'orizzonte degli eventi e, perché no, anche il modo di uscirne. Per adesso, però, impariamo a costruirlo.

I buchi neri, a parte la difficoltà di trovare il miglior modo per rappresentarli, sono sicuramente  gli oggetti più perfetti dell’Universo (non l’ho detto solo io…). Bastano infatti tre soli parametri per caratterizzarli: massa, carica elettrica e momento angolare. Nel caso più semplice che stiamo trattando, ne basta uno solo: la massa. Questo fatto porta a una conclusione straordinaria e unica: qualsiasi sia il tipo di materia che forma un buco nero, degenere o non degenere, salata o non salata, solida o liquida, non ha alcuna importanza (un vero deposito i rifiuti, dove non interessa la differenziazione…). Le caratteristiche finali dell’oggetto non cambiano di una virgola. Qualsiasi informazione su ciò che è stato inghiottito viene persa. Questa peculiarità ha portato al ben noto slogan: “I buchi neri non hanno capelli (black holes have no hairs)”.

Un oggetto, perciò che potrebbe anche considerarsi estremamente semplice, almeno per quanto riguarda le sue proprietà fisiche. L’unica cosa che dobbiamo cercare di esprimere al meglio è il suo inserimento in un diagramma altrettanto semplice, che possa, alla fine, portare ben più lontano dello spazio che lo circonda.

Con la metrica di Schwarzschild siamo riusciti a descrivere sia l’interno che l’esterno di un buco nero (ossia fuori e dentro l’orizzonte), ma si può fare di meglio e di più. Traiettorie che possono solo andare o provenire dall’infinito, coni di luce che si piegano e/o si stringono. Difficoltà che possono e devono essere superate, qualsiasi siano le modalità di formazione. Ricordiamo, infatti, che il buco nero stellare deriva da una storia ben definibile (una massa si contrae fino a che il suo raggio diventa minore dell’orizzonte degli eventi). In realtà, però, non ci sarebbe nemmeno bisogno di una massa che si contragga, basterebbe avere una massa  tale che l’orizzonte degli eventi sia esterno alla sfera che la contiene. Il caso classico è quello dei buchi neri galattici. Non dimentichiamo, infatti, che il raggio di Schwarzschild dipende solo e soltanto dalla massa della sfera: il buco nero non ha capelli…

Ricordiamo, inoltre, che la metrica di Schwarzschild descrive, finché può, ciò che si vede da un sistema in quiete esterno, che non risenta del campo gravitazionale. Chi si avvicina al buco nero mostra a chi sta fermo un orologio che continua a rallentare, il che si traduce in qualcosa che non può raggiunge mai l’orizzonte degli eventi, se non all’infinito. In altre parole, una traiettoria che sembra dare sempre una possibilità di uscita a chi ha intrapreso un viaggio così rischioso.

L’orizzonte degli eventi rappresenta l’ultima via d’uscita, quella che è permessa solo alla luce. Non una vera via d’uscita, però, dato che la luce è costretta a restare sempre in quella posizione. E’ inutile che l’astronave aspetti il segnale di ritorno, dato che lo riceverà solo all’infinito. Permettetemi di azzardare un frase che potrebbe chiarire ciò che stiamo per andare a fare: l’orizzonte degli eventi è l’ultimo percorso effettuabile dalla luce prima di entrare nel buco nero.

Lo spaziotempo di Schwarzschild ammette, però, una soluzione ben più ampia di quanto sia stato detto finora, che affronteremo più “facilmente” in seguito. Detto in parole molto povere, la soluzione può essere ribaltata, cambiando il segno al tempo, con tutto ciò che ne può derivare. Avete sicuramente già capito di cosa sto parlando, ma ogni cosa a suo tempo.

Devo anticipare che sono stati fatti vari tentativi per descrivere lo spaziotempo attorno a un buco nero, partendo dalla metrica di Schwarzschild. Una piuttosto comune è quella che usa le coordinate di Kruskal–Szekeres. Attraverso una trasformazione di coordinate è come se si aprisse l’imbuto di Schwarzschild (al pari di un’anguria) e si appiccicasse su un piano. Ne viene fuori un diagramma simile a quello di Minkowski, estremamente interessante, ma che si porta dietro, comunque, i punti all’infinito che tutto hanno, meno che essere facilmente rappresentabili. Chi vuole andare a fondo di questa metrica, che già porta molto avanti, può leggere l’ottima spiegazione data su Wikipedia (inglese!) QUI

Il diagramma di Penrose

Noi, invece, facciamo un passo ancora più lungo, dato che siamo stati abituati a non spaventarci dei punti all’infinito, perfino quando abbiamo introdotto il corso di matematica elementare.

Guardiamo con occhio molto critico lo spaziotempo di Minkowski. Esso rappresenta uno spaziotempo infinito e, di conseguenza possiede molti punti all’infinito: quelli delle curve tipo spazio, quelle delle curve tipo tempo e quelle delle curve tipo luce.

Partiamo da lontano e costruiamo un diagramma semplicissimo, composto da due fasci di linee rette e parallele tra loro… (Fig. 7).

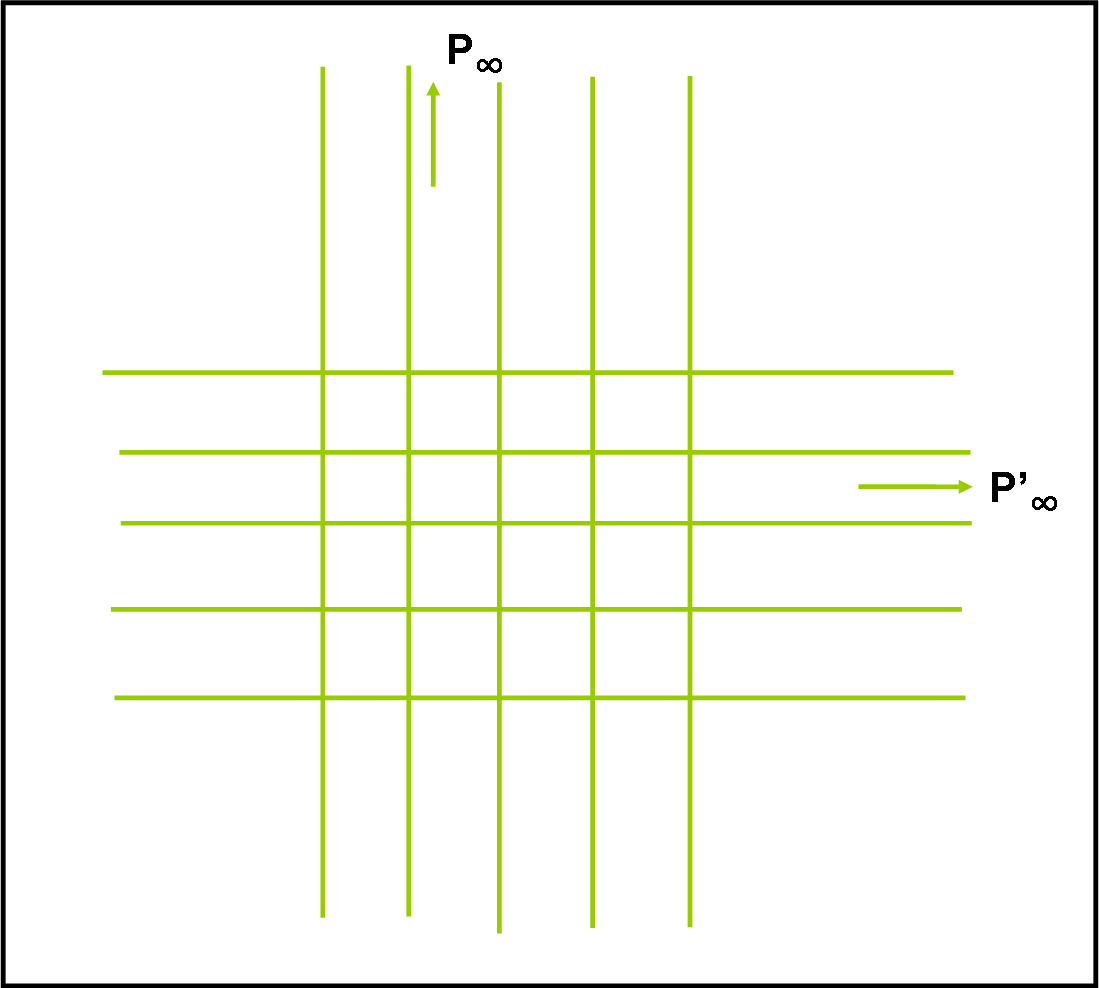
Tanti binari paralleli, in due direzioni perpendicolari. Vi è una tecnica tipica dell’architettura più sofisticata che riesce a disegnare ciò che vede un osservatore in qualsiasi punto si trovi: la prospettiva. In parole terra-terra, le rette verticali andranno tutte verso un punto all’infinito, così come quelle orizzontali (Fig. 8). Perché allora non disegnare questi punti immaginari come veri e propri punti? La linea che passa per loro la conosciamo molto bene, ed è la retta all'infinito.

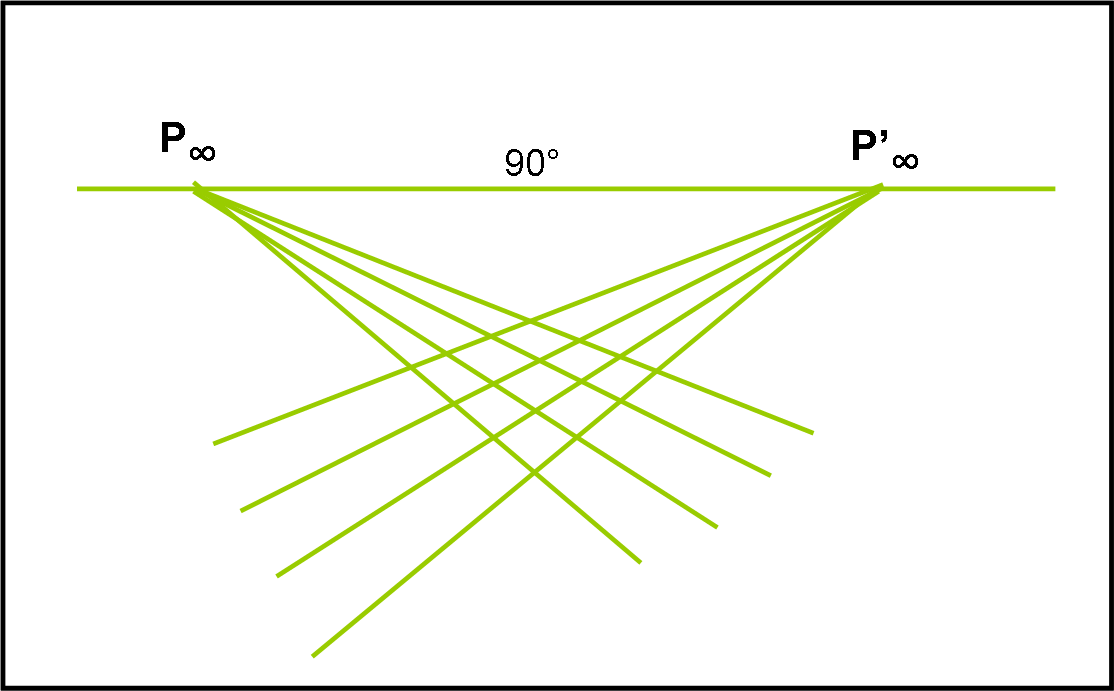
Ovviamente le distanze sulle rette che portano a loro non si mantengono, nel senso che gli stessi segmenti vicini a noi sembrano molto più lunghi di quelli che vediamo in lontananza. Tuttavia, se a noi non interessasse la misura di ciò che osserviamo, ma solo la causalità degli eventi che vengono rappresentati, non sarebbe un grosso problema. Proviamo a estendere la rappresentazione anche “alle nostre spalle”, ossia i binari convergono non solo davanti a noi, ma anche dietro. Otteniamo così quattro punti all’infinito .  Immaginiamo, ancora, di considerare le linee verticali come linee del tempo e quelle orizzontali come linee dello spazio. La figura diventa un qualcosa di estremamente semplice: le linee verticali e orizzontali si curvano per finire nei punti all'infinito (Fig. 9).

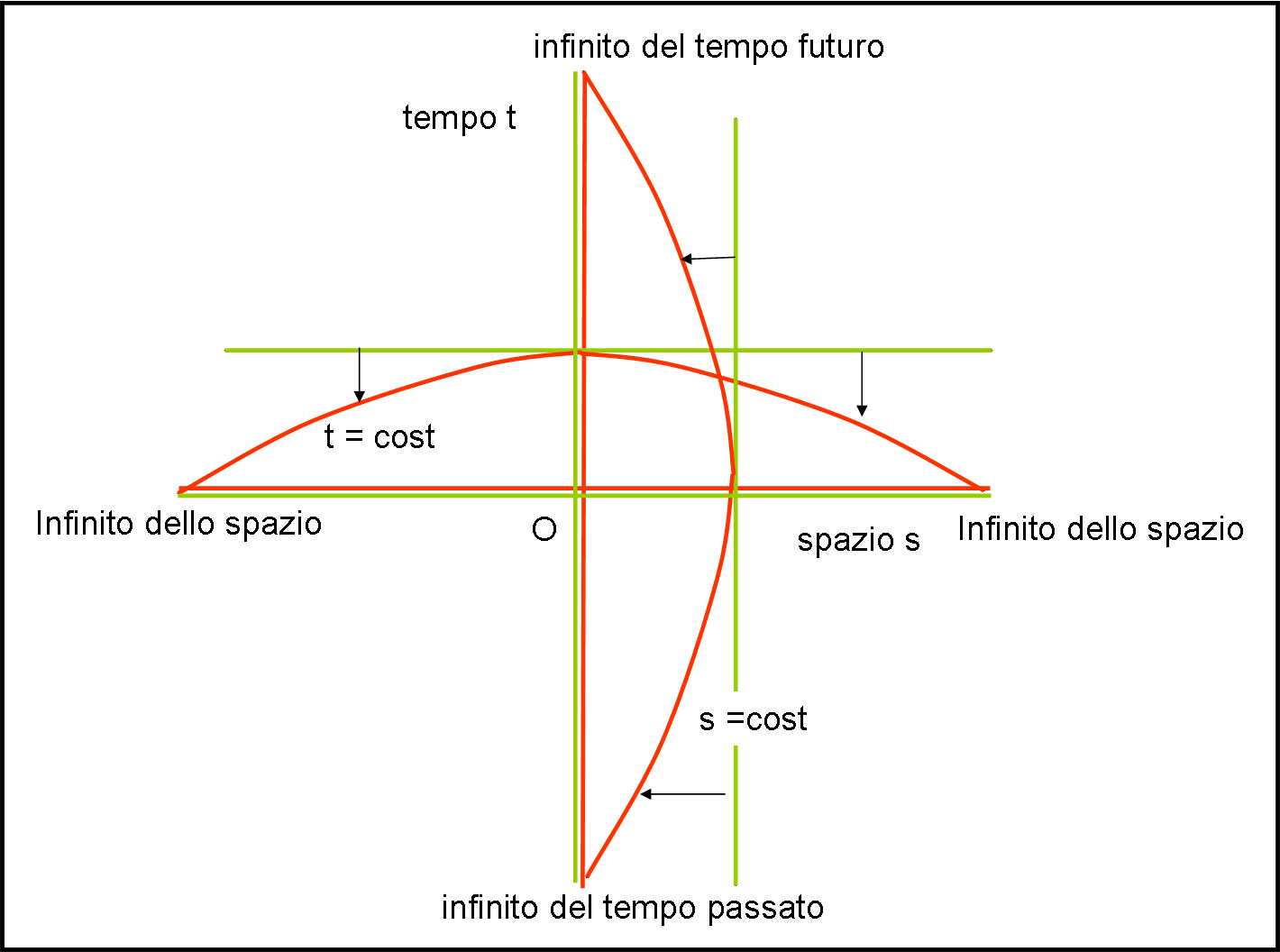
A questo punto possiamo tranquillamente collegare tra loro, in Fig. 10, i punti all’infinito e ottenere un quadrato. I lati del quadrato, dato che uniscono punti all’infinito, sono anch’essi situati all’infinito e rappresentano la linea all'infinito dello spaziotempo (infinito futuro e infinito passato)

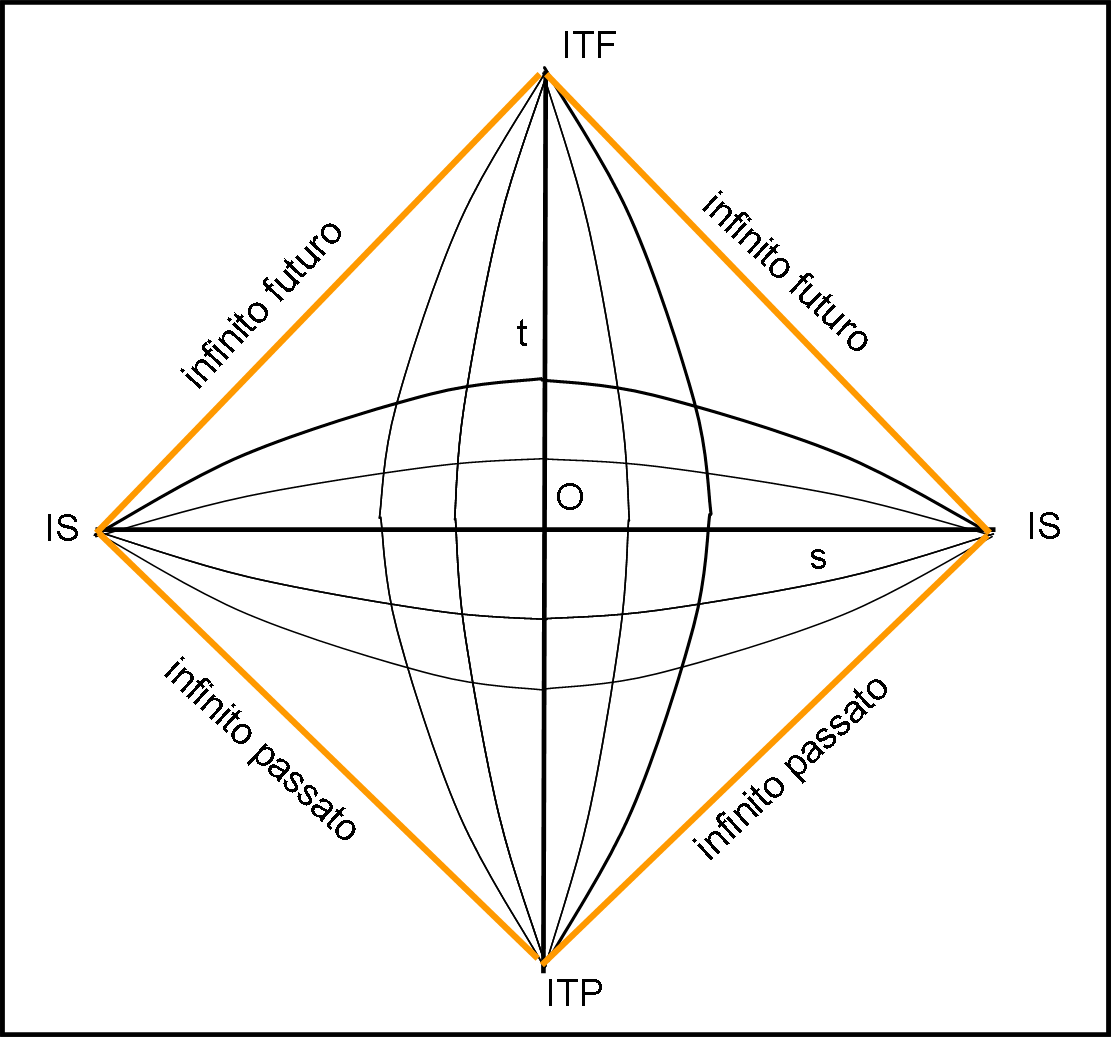
L’effetto più “visibile” di questa operazione è che le linee del passato e del futuro, descrivibili nello spazio a un tempo t, saranno delle curve e non più rette orizzontali parallele come nello spazio-tempo di Minkowski. In altre parole è come se “stringessimo” lo spazio, rappresentando concretamente i suoi punti all’infinito e facendo convergere le rette parallele proprio verso questi punti. Non possiamo stupirci, dato che ogni retta "parallela" deve andare a finire nello stesso punto. Un’analoga operazione possiamo effettuarla per l’asso del tempo. In questo caso le linee descritte da un corpo fermo nello spazio, saranno curve che terminano nei punti all’infinito del passato e del futuro. Esse sono le curve per cui lo spazio s e il tempo t e sono costanti.

Tutto ciò non è altro che lo spaziotempo di Minkowski, dove abbiamo mantenuto la causalità e dove abbiamo sacrificato la conoscenza della lunghezza dei vari segmenti (volendo, però si potrebbero anche ricostruire). Le linee curve orizzontali e verticali non sono altro, ovviamente, che le linee tipo spazio e tipo tempo.

A questo punto, chiediamoci: "Cosa sono mai le linee che uniscono i quattro punti fondamentali?" Ebbene, lo sappiamo bene: la linea dei punti all’infinito. Ma quali sono le linee più famose che partono dall’infinito e terminano all’infinito? Beh… le linee tipo-luce. In poche parole, la retta a 45° rispetto ai due assi che uniscono i quattro vertici è sicuramente una linea tipo-luce e tali e quali sono le rette parallele a lei. Le linee tipo-luce restano delle rette!

Pensiamoci un attimo e scopriamo, subito, che i coni luce si sono mantenuti tali e quali, sempre formati da rette a 45° rispetto alle rette tipo tempo e tipo spazio. La nostra trasformazione è una trasformazione conforme, dato che mantiene gli angoli e lascia le linee tipo luce rettilinee. Per ottenere ciò non abbiamo fatto altro che stirare e stringere le distanze temporali e spaziali (Fig. 11)

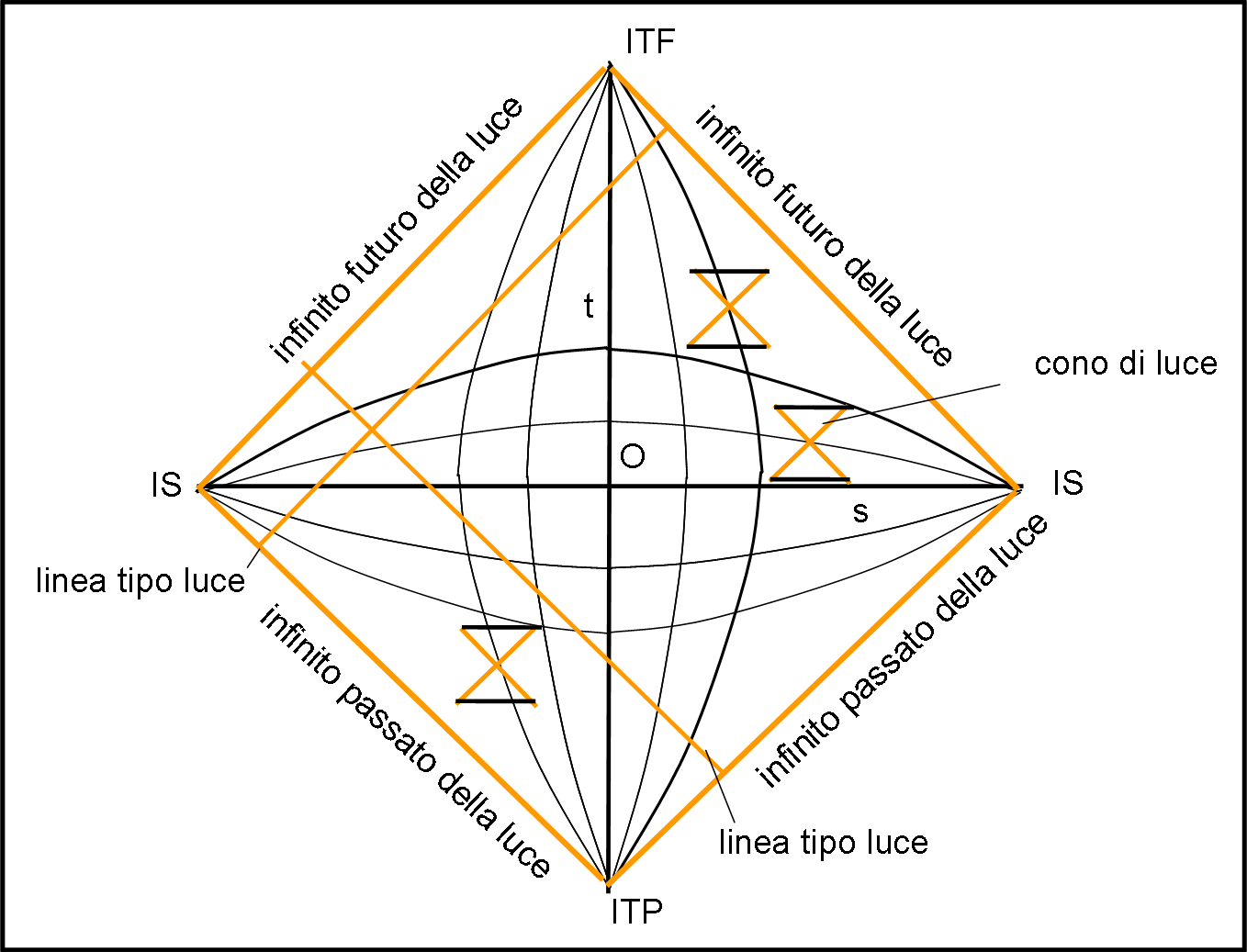
Notiamo, anche, che una geodetica tipo tempo non è altro che un punto che si muove in modo inerziale e la geodetica tipo spazio non è altro che la “comune” retta della geometria di tutti i giorni. Le linee tipo luce , chiamate anche geodetiche nulle, dato che il tempo trascorso su una di queste linee è nullo, non è altro che la traiettoria di un fotone lasciato libero di muoversi.

Diciamo anche che i lati del quadrato possono essere considerati come l’infinito passato e futuro della luce.

Un’idea quasi banale, ma sicuramente geniale.

Il contorno del nostro quadrato rappresenta perfettamente tutto ciò che è infinito nello spaziotempo. Ciò non toglie che si possa lavorare tranquillamente al suo interno, con regole semplici e ben note, come coni di luce non deformati.

Basta considerare un certo evento E e seguire una sua traiettoria percorsa a velocità inferiore a quella della luce. In ogni suo punto possiamo tracciare, come sempre la linea relativa alla luce.

Spieghiamoci meglio…

Come ormai abbiamo capito, le geodetiche tipo tempo cambiano continuamente la loro direzione, passando da un evento a un altro. Preso qualsiasi evento della linea di Universo, si consideri la tangente alla curva nell’evento. Questa tangente deve sempre fare un angolo minore di 45° rispetto alla linea verticale.  E questo deve valere per qualsiasi evento che compone la geodetica tipo tempo (Fig. 12).

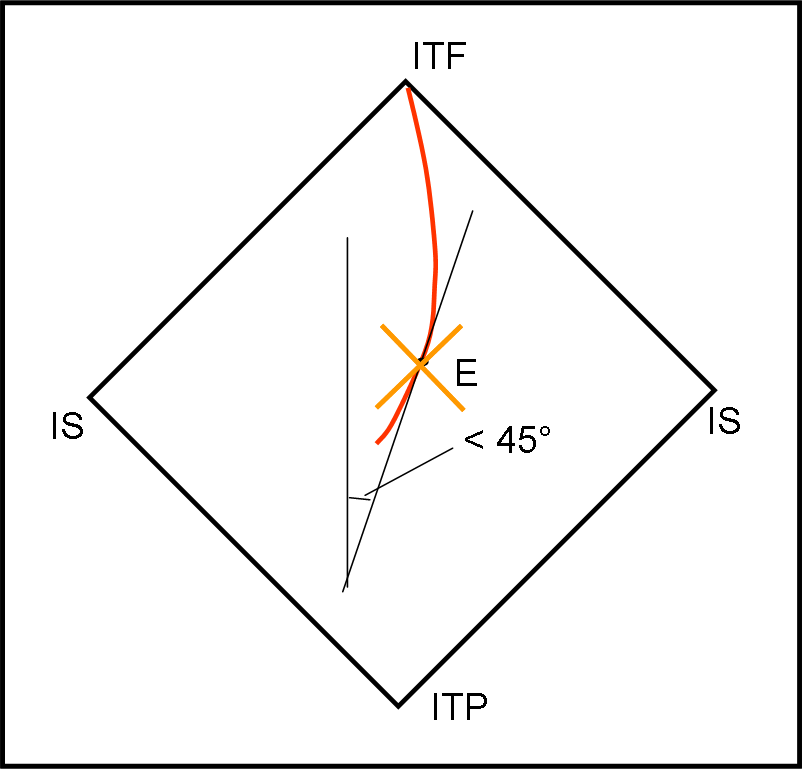
Prima di proseguire, digeriamo bene il diagramma super compatto di Fig. 11 e riassumiamo le sue caratteristiche fondamentali:

1) Il tempo continua a scorrere lungo la verticale e lo spazio a 90° da lui.

2) Le linee tipo luce formano sempre 45° con il tempo e lo spazio. Le linee di Universo (tipo tempo) formano sempre angoli inferiori a 45° con l’asse del tempo. Le linee tipo spazio formano, invece, un angolo maggiore di 45°.

3) Gli stessi intervalli disegnati sulle varie curve non rappresentano distanze o tempi uguali: un centimetro al centro diventa, dopo poco, un chilometro e, addirittura, infinito quando un estremo è infinito.

Provate a pensare come può essere rappresentato un buco nero stellare con una sua evoluzione fisica… ma non andate a copiare, mi raccomando!

 

QUI un approfondimento sulle singolarità

In attesa di essere riuniti in un unico approfondimento, QUI trovate tutti gli articoli della serie "Apriamo la porta del buco nero" finora pubblicati