Per una trattazione completa di questo argomento, si consiglia di leggere il relativo APPROFONDIMENTO nel quale è stato inserito anche il presente articolo

 

Questo articolo rappresenta la soluzione del quiz che è valso un premio Nobel al grande Michelson. Tuttavia ne ho approfittato per spiegare l’esperimento che ha cambiato la fisica (oltre che essere un fallimento… ma ce ne fossero tanti così!), in modo veramente elementare, sotto forma di una favola. Ciò ha comportato qualche inesattezza, che giudico, però, di secondaria importanza rispetto al concetto di fondo. Seguirà tra breve l’articolo “serio” che metterà le cose a posto. Per adesso, seguendo il nostro stile, giudico la favola vietata ai maggiori di X anni, con X che tende a infinito…

In un mondo incantato (il nostro Universo), esistono due strani folletti, che ormai conosciamo molto bene, avendoli spesso chiamati per nome: fotoni. Essi sono molto allegri e spesso dispettosi, ma hanno un compito veramente straordinario, quello di trasportare la luce. Senza di loro non potremmo vedere né i nostri familiari, né gli animali, le piante, il nostro pianeta, il Sole, le stelle e le galassie. Insomma, saremmo completamente ciechi. I fotoni sanno quanto sono importanti, per cui cercano di correre al massimo delle loro possibilità. Ci riescono benissimo, in quanto, nell’Universo, non c’è niente che vada più veloce di loro. Essi percorrono, infatti, ben 300 000 chilometri in un secondo, ossia raggiungono quella che noi chiamiamo velocità della luce.

Un lavoro veramente stressante. Pensate che per riuscire a raggiungere questa velocità in modo costante essi non si devono fermare mai. Anzi, possono esistere solo se corrono sempre al massimo. Non potremo mai dirgli grazie abbastanza e gli si possono facilmente perdonare alcuni scherzi e giochi che compiono con i loro amici elettroni.

Bene… conosciuti i nostri due eroi, vediamo per cosa un certo grande scienziato di nome Michelson pensò di utilizzarli. Potremmo considerarlo un vero mago con i suoi due assistenti…

Innanzitutto, un po’ di storia molto semplice. Il comportamento dei fotoni è alquanto bizzarro, come si diceva prima. Essi, a volte, sembrano delle vere e proprie particelle, ma, altre volte, si comportano come onde (questa favola ce l'hanno raccontata Fotino e i suoi fratelli) e gli scienziati hanno cambiato idea molte volte a riguardo. In realtà le due cose sono del tutto compatibili, ma ai tempi del nostro scienziato non si era ancora compresa appieno questa capacità dei piccoli fotoni (e di molti altri loro piccoli amici). A quei tempi si parlava di onde, come quelle del suono, capaci di trasmettere i rumori. Onde, capaci di trasmettere la luce.

Tuttavia, sorgeva un grave problema: le onde del suono si propagano perché c’è l’aria. In parole ancora più semplici: loro mettono in vibrazione l’aria che ondeggia, appunto, e permette di trasportare il segnale rumoroso. Qualcosa di molto simile alle onde del mare che si propagano nell’acqua e la fanno alzare ed abbassare al loro passaggio.

Il che voleva dire che se la luce, intesa come onda, poteva viaggiare tra le stelle e arrivare fino ai nostri occhi, doveva esistere una specie di acqua o aria che potesse vibrare. Un qualcosa che doveva impregnare tutto l’Universo. Gli scienziati l’avevano chiamata etere, una specie di sostanza molto rarefatta che non desse fastidio al movimento dei corpi celesti, ma che permettesse, comunque, di poter vibrare e trasportare le onde luminose.

Il signor Michelson decise di provare l’esistenza dell’etere attraverso l’utilizzo dei suoi due fotoni sempre disponibili a giocare. Per non complicare troppo le cose, immaginiamo che i fotoni siano proprio particelle che continuino a saltellare su è giù rispetto a una linea diritta, in modo da simulare un’onda dell’etere che si alza e si abbassa, come vediamo nella Fig. 1.

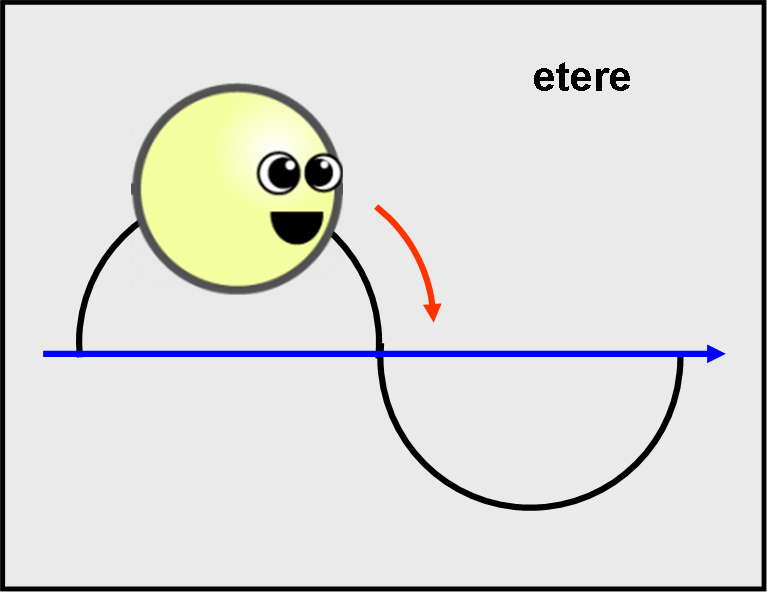
Lo stesso signor Michelson pensò che la Terra, durante il suo moto attorno al Sole, doveva muoversi attraverso l’etere, immaginato sempre immobile, e, quindi, doveva succedere la stessa cosa che a noi capita quando corriamo velocemente. Anche se non c’è vento, sentiamo l’aria che ci sbatte in faccia. In questo modo ci accorgiamo che attorno a noi c’è aria, qualcosa di materiale, anche se è talmente rarefatta da non accorgercene normalmente, quando siamo fermi. La stessa cosa doveva succedere alla nostra Terra mentre si muoveva attorno al Sole. Lei viaggiava nell’etere e quindi muovendosi a una certa velocità doveva venire investita dall’etere che le sbatteva contro, come viene rappresentato in Fig. 2.

In poche parole se la Terra si muovesse con una certa velocità, è come se fosse considerata ferma e venisse investita da un vento di etere con pari velocità, ma diretta in senso contrario al moto della Terra. La stessa cosa che capiterebbe se, correndo, pensassimo di essere fermi e sentissimo il vento dell’aria colpirci con la stessa velocità con la quale in realtà stiamo correndo.

Ovviamente, se esisteva l’etere, anche i due fotoni scelti da Michelson dovevano subire l’effetto dell’etere. Se viaggiavano nella direzione del moto della Terra sarebbero stati investiti dal vento dell’etere e avrebbero dovuto trovare un po’ di resistenza nel correre, se invece fossero andati in senso contrario sarebbero stati aiutati nella loro corsa.

Per spiegare ancora meglio l’esperimento di Michelson, immaginiamo di essere nei pressi di un fiume. Esso ha una certa corrente, ossia la sua acqua è trascinata verso una direzione (dalla sorgente alla foce). La corrente del fiume simula molto bene ciò che fa il vento dell’etere: un qualcosa che si oppone al movimento se si va controcorrente e che l’aiuta se va in favore di corrente.

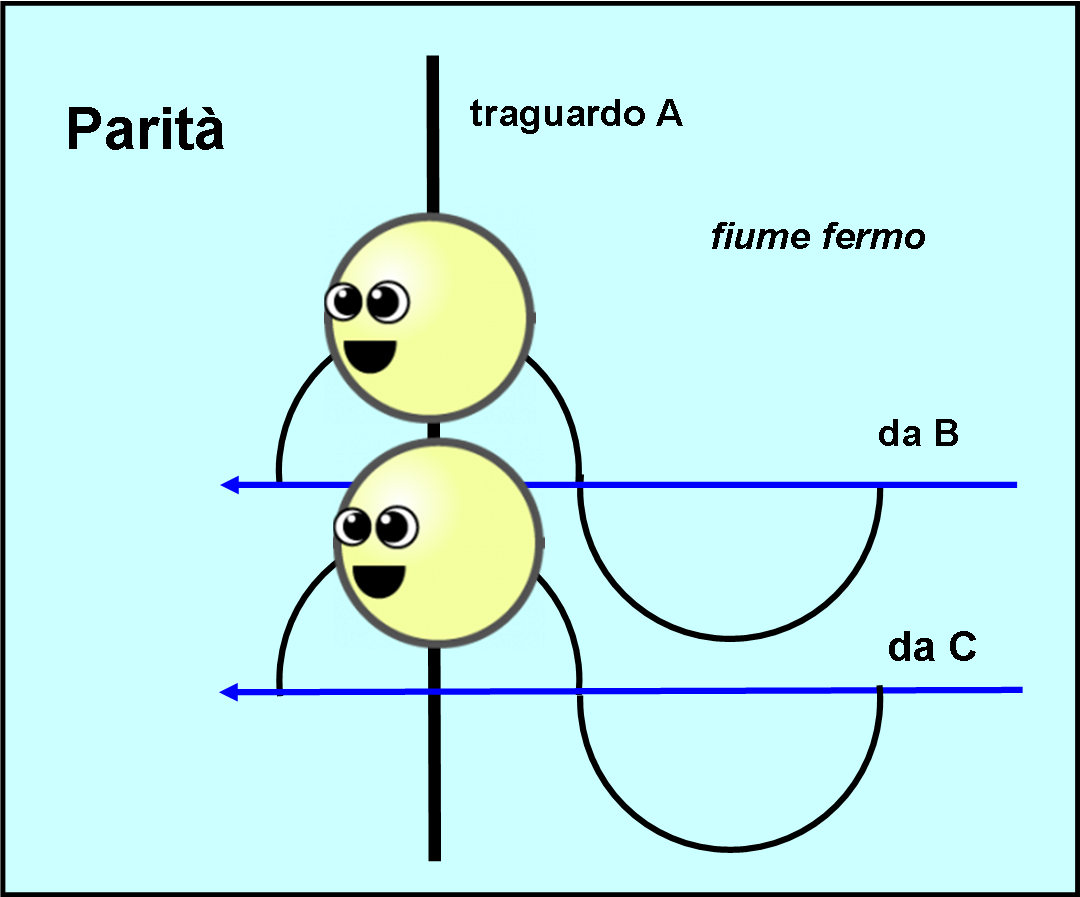
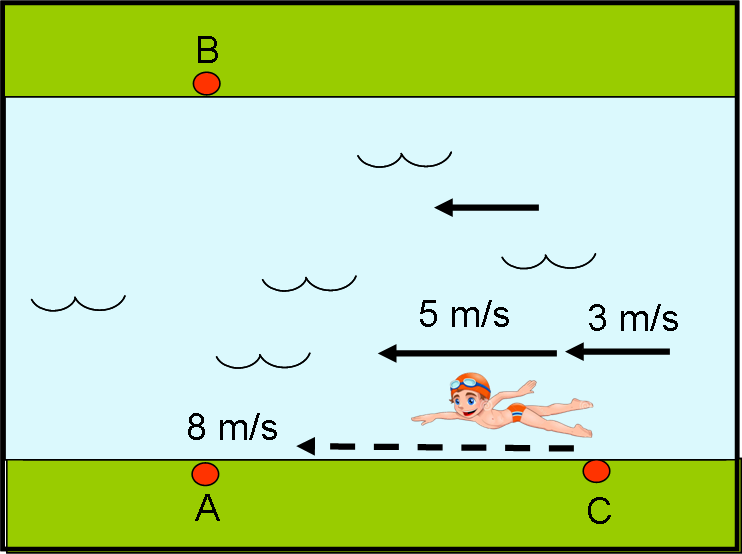
Prendiamo due nuotatori, ossia i nostri due fotoni. Con un colpo di bacchetta magica blocchiamo la corrente del fiume in modo che esso diventi una piscina con l’acqua immobile. Dopodiché impostiamo una bella gara tra i due fotoni N e N’ (travestiti da veri nuotatori), come mostra la Fig. 3. Il primo deve partire da A, attraversare il fiume, toccare B e tornare esattamente indietro in A. Il secondo deve, invece, percorrere la distanza da A e C, vicino alla riva del fiume, e tornare in A. La distanza tra A e C (d) è ESATTAMENTE uguale a quella tra A e B. Vince la gara chi arriva per primo.

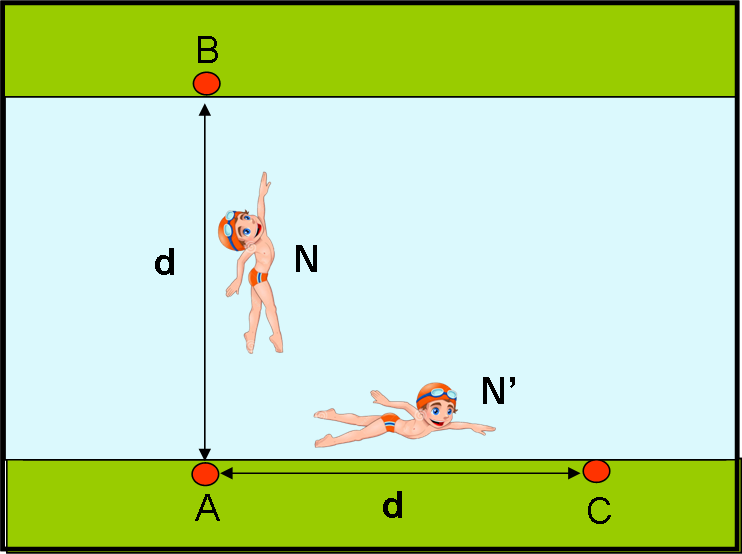
I fotoni sono contentissimi di questo gioco e non vedono l’ora di eseguirlo. Partono nello stesso istante da A e, saltellando, saltellando (nuotando, nuotando), tornano al punto di partenza. Michelson si accorge della parità dato che i fotoni effettuano lo stesso identico saltello quando arrivano al traguardo. L’acqua è ferma, le distanze uguali e la velocità dei fotoni esattamente la stessa (tutti i fotoni viaggiano alla stessa velocità): non poteva ottenere niente di diverso (Fig. 4).

Fin qui tutto bene. Adesso, la faccenda si complica, dato che al fiume viene permesso di scorrere tranquillamente. In altre parole, inseriamo il vento dell’etere, ossia la corrente del fiume. Vediamo passo dopo passo cosa capita ai nostri due fotoni. Consideriamo per primo quello che attraversa il fiume (Fig. 5a).

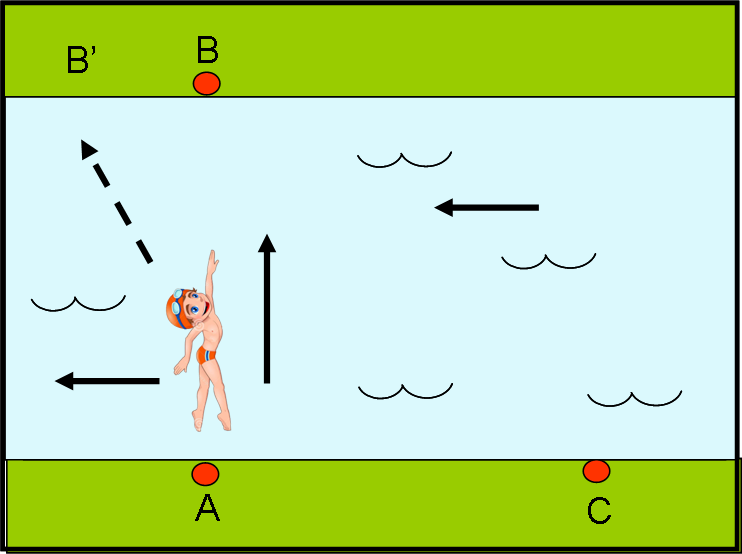
Il fotone non è uno sprovveduto e sa benissimo che se si dirigesse nella direzione in cui vede B alla partenza sarebbe ben presto trascinato dalla corrente verso sinistra e toccherebbe l’altra sponda in un punto diverso (B’). I fotoni sono piccolissimi, ma molto intelligenti e non è da meno il nostro nuotatore. Lui sa che deve dirigersi contro corrente di un certo angolo (verso B”), in modo che la sua velocità in quella direzione si sommi a quella della corrente del fiume e lo porti esattamente in B (Fig. 5b).

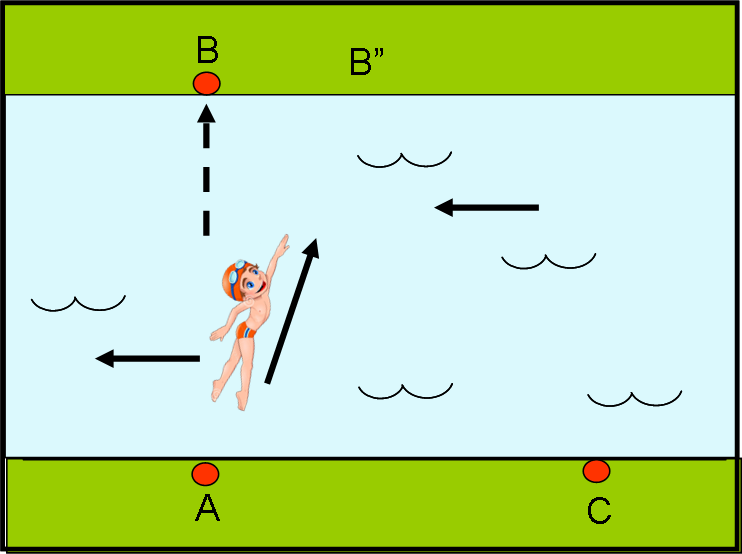
Mentre va verso destra viene costantemente spostato verso sinistra dalla corrente fino a raggiungere esattamente B. La stessa cosa deve fare al ritorno in modo perfettamente simmetrico (Fig. 5c).

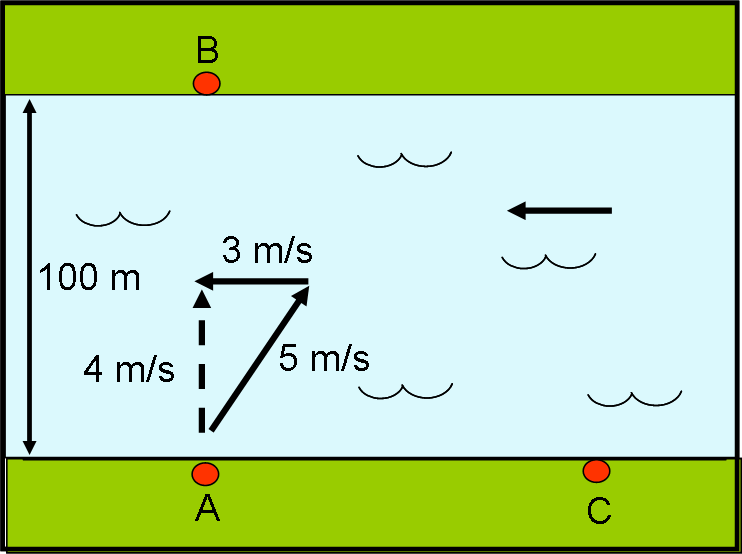
Per coloro che conoscono il teorema di Pitagora è facile capire a che velocità va effettivamente il fotone. Se, ad esempio, la sua velocità fosse 5 m/s e quella del fiume 3 m/s, si otterrebbe una velocità di 4 m/s (√(5² – 3²) = √ (25 – 9) = √16 = 4), come mostrato in Fig. 6.

Ipotizzando un fiume largo 100 m, per raggiungere B il primo fotone impiegherebbe esattamente 25 secondi. Il ritorno sarebbe identico e quindi il traguardo sarebbe toccato dopo 50 secondi. Notiamo che il tempo impiegato sarebbe decisamente più lungo di quello ottenuto con il fiume fermo. In quel caso la velocità sarebbe sempre di 5 m/s e quindi l’andata e il ritorno si percorrerebbero entrambi in soli 100/5 = 20 secondi. Il tempo totale sarebbe di 40 secondi.

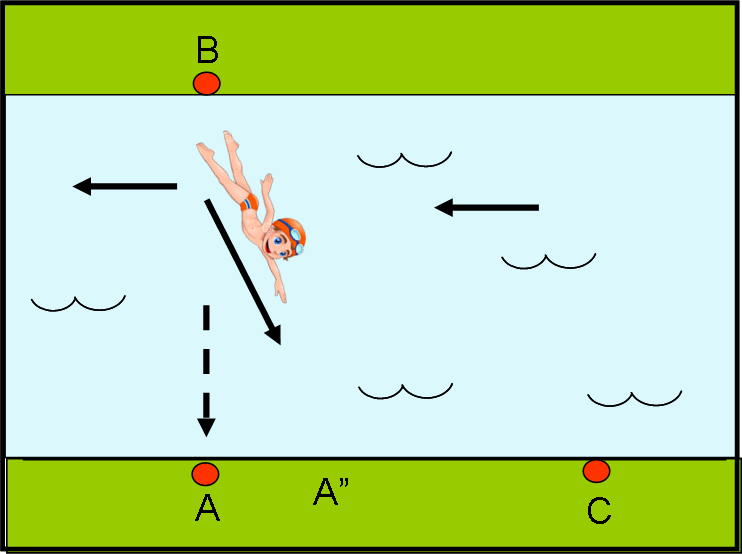
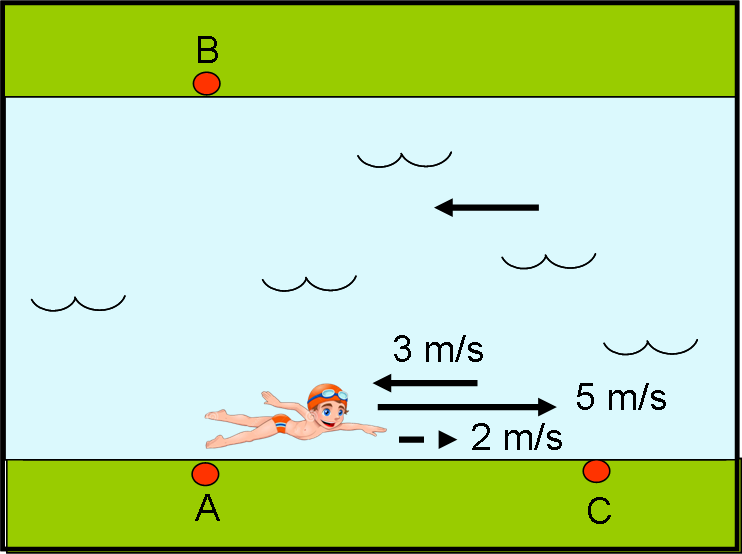
Vediamo, adesso, cosa succede al fotone che nuota lungo la sponda del fiume. Lui deve raggiungere C, andando in linea retta e alla velocità di 5 m/s, ma viene investito dalla corrente che cerca di trascinarlo indietro di 3 m/sec. In poche parole, in un secondo lui percorrerebbe 5 metri, ma sarebbe portato indietro di 3 metri. In conclusione, è proprio come se nuotasse a 5 – 3 = 2 m/s (Fig. 7a).

Per raggiungere C deve faticare molto e vi arriverebbe dolo 100/2 = 50 secondi (ricordiamo che la velocità si misura in metri diviso secondi, per cui dividendo i metri per la velocità si ottengono proprio i secondi impiegati).

Fortunatamente, il ritorno è decisamente più facile… Adesso, la corrente del fiume va nel verso del nuotatore e l’aiuta a spostarsi più velocemente. In un secondo il fotone percorrerebbe 5 metri, ai quali si aggiungono i 3 metri della corrente. Ne segue che il nuotatore si muove alla considerevole velocità di 5 + 3 = 8 m/s. I 100 metri del ritorno sarebbero, perciò, percorsi in solo 100/8 = 12.5 m/s (Fig. 7b).

Una vera saetta, ma… ormai è troppo tardi. Sommando i 50 dell’andata si ottiene un risultato finale di 50 + 12.5 = 62.5 secondi. Il secondo fotone arriverebbe al traguardo ben 12.5 secondi dopo l’arrivo del primo. Con pochi calcoli si potrebbe facilmente capire, da questo risultato, quanto vale la corrente del fiume, ossia quanto vale il vento dell’etere e - soprattutto - se esiste.

Parlando di velocità comparabili tra loro (3 e 5 metri al secondo), la gara avrebbe un netto vincitore e tutti i calcoli potrebbero essere fatti in modo banale. Ma, allora, perché dare un premio Nobel a un signore che ha inventato una gara così elementare e controllabile? Il fatto è che la differenza tra velocità del nuotatore e velocità della corrente del fiume è decisamente grande. I fotoni “nuotano” a 300 000 chilometri al secondo, mentre la Terra (e quindi il vento dell’etere) si muove a 30 chilometri al secondo. Il loro rapporto è 10 000, ossia i fotoni viaggiano 10 000 volte più veloci del vento dell’etere.

Questo fatto comporta una differenza tra i tempi impiegati dai due fotoni, praticamente impossibile da misurare ai tempi di Michelson (fine ottocento!).

Tuttavia, egli ebbe l’idea geniale che gli permise di ottenere il Nobel. Conoscendo bene i suoi due fotoni sapeva quanto velocemente riuscissero a saltellare sopra e sotto una linea diritta. Questi saltelli duravano pochissimo e tra il punto più alto di un saltello e quello del successivo saltello il tempo era dello stesso ordine della differenza di tempo impiegato dai due nuotatori. Guardando attentamente il punto A (di fine corsa) Michelson si sarebbe accorto che nell’istante in cui il primo fotone raggiungeva il punto più alto del saltello, il secondo sarebbe stato in ritardo e vicino al punto più basso. Questa differenza era facile da vedere e anche da fotografare. Una specie di fotofinish di una corsa ciclistica, analizzabile con molta calma e precisione.

Ovviamente, Michelson non usò un fiume, ma uno strano macchinario che mandava i fotoni in direzioni perpendicolari tra loro in modo da raggiungere una distanza uguale e tornare indietro. Ma il primo avrebbe subito il vento dell’etere come il nuotatore che ha attraversato il fiume; il secondo sarebbe andato nel verso del moto della Terra, ossia controcorrente nel fiume. Quest’ultimo sarebbe arrivato in ritardo di mezzo saltello circa! In tal modo, il nostro premio Nobel avrebbe potuto misurare, analizzando i saltelli (in parole tecniche la lunghezza d’onda), la velocità dell’etere, come fatto per la corrente del fiume (Fig. 8).

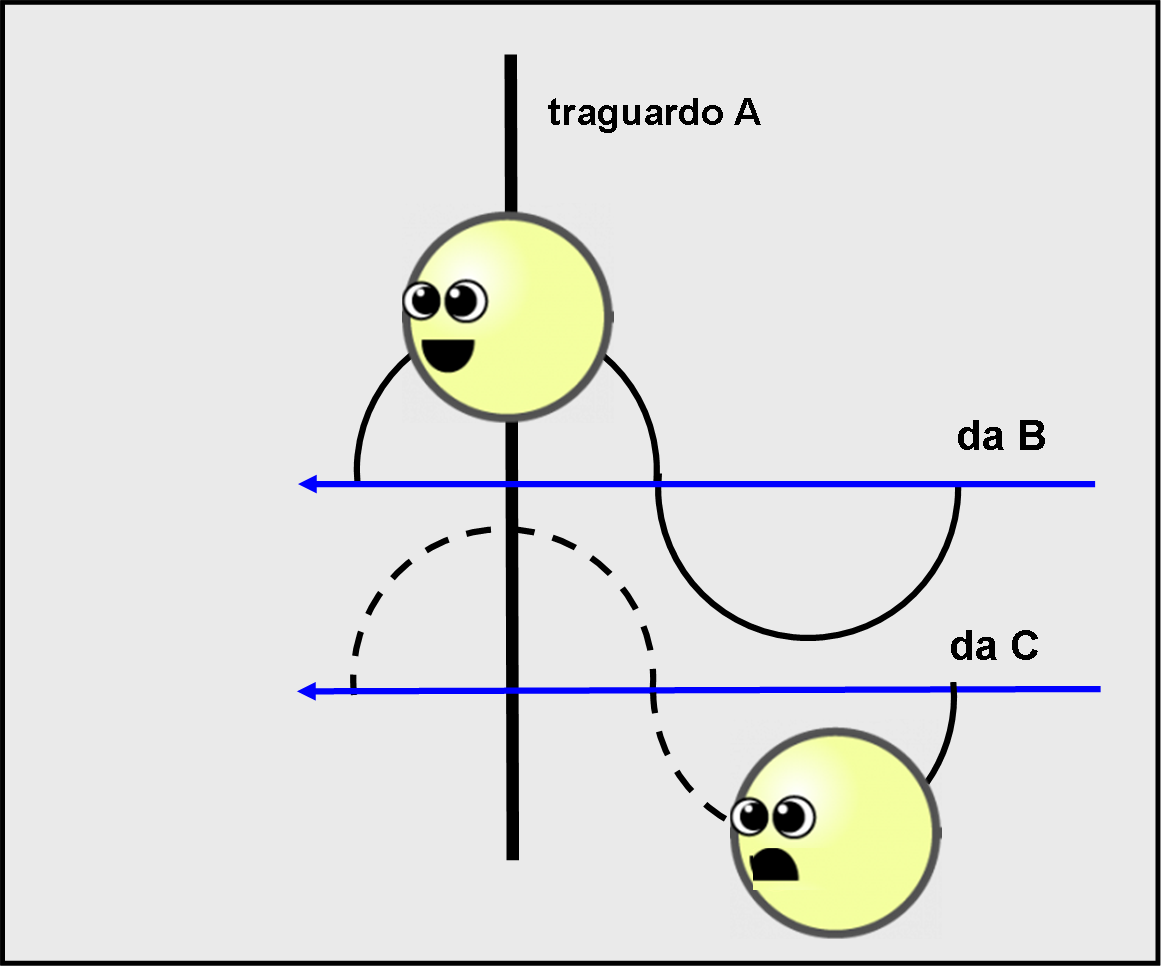
Più correttamente, i saltelli del secondo fotone sarebbero “sfasati” rispetto ai quelli del primo. Lo sfasamento, in realtà piccolissimo, si sarebbe, però, potuto misurare facilmente analizzando la luce che colpiva il traguardo, dove i due fotoni erano giunti.

Spieghiamoci meglio... Il secondo fotone arriva in ritardo rispetto al primo, ma la differenza di tempo è impossibile da misurare con un orologio. Tuttavia, in quella differenza di tempo così piccola, i fotoni sono capaci di effettuare almeno un saltello o poco meno. Ciò vuol dire che il secondo fotone arriva al traguardo dopo aver compiuto circa mezzo saltello in più (ha impiegato più tempo). La luce combinata dei due fotoni riesce a evidenziare questo sfasamento e valutare la differenza di tempo senza usare un orologio, ma solo attraverso lo sfasamento tra i saltelli. Invece del tic-tac dell'orologio si usa il rapidissimo tic-tac dei saltelli, molto più preciso e "facilmente" osservabile sulla linea del traguardo.

Tutto bene? Nemmeno per sogno! Compiendo l’esperimento nelle condizioni migliori a variando anche le direzioni dei due fotoni rispetto al moto della Terra (ossia della direzione del vento dell’etere) i due fotoni arrivavano sempre insieme al traguardo. Tutto succedeva come se non ci fosse corrente nel fiume, ossia come se la Terra non si muovesse. Dato, però, che la Terra si muove sicuramente, l’unica soluzione fu che non esisteva l’etere e quindi nemmeno il suo vento che favoriva o sfavoriva le due “nuotate”.

Un esperimento fallito, sicuramente, ma che permise di inventare un sistema per misurare differenze di tempo (e/o di metri) impossibili prima di allora. L’apparecchio di Michelson venne chiamato interferometro e si usa ancora adesso. Inoltre, la “scomparsa” dell’etere cambiò completamente la fisica dell’epoca, dimostrando che le onde luminose si propagano anche nel vuoto e che la velocità della luce resta sempre la stessa in qualsiasi sistema di riferimento si misuri: si era aperta la porta verso la relatività di Einstein.

Ma questa è tutta un’altra favola…

 

La storia continua continua QUI con la descrizione del celeberrimo esperimento di Michelson e Morley