Dall’opera di Tolomeo si evince un concetto fondamentale: i moti circolari uniformi sono riservati alle sfere celesti, mentre i moti rettilinei sono propri del mondo sublunare. Non parliamo poi di quelli non uniformi.  In pratica, un altro confine ben delimitato tra la Terra, posta al centro dell’Universo, e i movimenti degli altri pianeti.  Bene, esiste un teorema, detto di Copernico, che riesce a dimostrare come moti circolari possano produrre un moto rettilineo. Ma era proprio di Copernico…? In ogni modo questo argomento permette di divertirsi  a costruire illusioni ottiche e ad avvicinarsi strettamente ai quiz sulle monete che rotolano una sull’altra, su cui stanno lavorando alacremente i nostri maghi.

Il teorema di cui stiamo per parlare si attribuisce solitamente a Copernico. Lui lo ha sicuramente generalizzato, ma è interessante notare che più di due secoli prima, lo stesso teorema era stato enunciato da un grande  astronomo arabo, Al-Tusi (1201-1274). Pur rimanendo ancorato alla teoria tolemaica, lui fu il primo a unire il moto rettilineo con quello circolare.

Noi cerchiamo di semplificare il tutto, cercando anche di creare illusioni ottiche e permettendoci di dimostrarlo in modo … moderno.

Torniamo alle nostre monete girovaghe e mettiamoci nel caso proposto da Oreste e risolto immediatamente da Andy: una moneta più piccola rotola all’interno di una circonferenza di raggio maggiore. In geometria la curva descritta da un punto qualsiasi del bordo esterno della moneta piccola viene chiamata ipocicloide (su queste curve vorrei tornarci in modo molto più generale, per cui non affondo il colpo…). Bene , il teorema di Copernico (o -meglio- di Al-Tusi) dice che se il raggio della circonferenza più piccola è la metà di quello della più grande, il moto del punto descrive una linea retta con un moto armonico (avanti e indietro).

Dimostrato questo teorema allargheremo il discorso e vedremo come Copernico sia riuscito a introdurre in qualche modo il moto ellittico. Niente di conclusivo, ma un primo passo verso Keplero.

Seguiamo, passo dopo passo, la dimostrazione del teorema, in modo più semplice di quanto fatto dallo stesso Copernico.

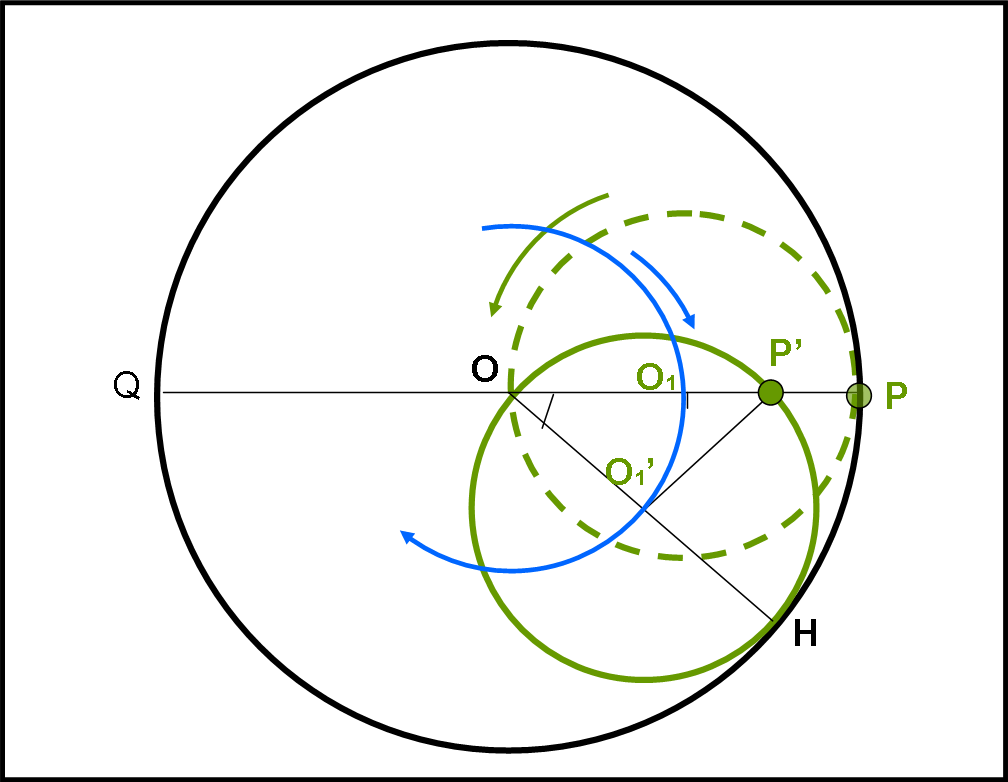
Nella figura che segue, disegniamo la circonferenza nera più grande di centro O. Al suo interno facciamo rotolare senza strisciare la circonferenza verde piccola che ha il raggio uguale alla metà di quella precedente.

In un certo istante, la circonferenza verde (tratteggiata) tocca la circonferenza grande in P, considerato come punto della circonferenza piccola (cerchietto verde). Cerchiamo di capire bene come avviene il movimento. La circonferenza verde ruota nel senso della freccia verde, rotolando lungo la circonferenza nera. Il centro O₁ della circonferenza verde descrive una circonferenza azzurra (di raggio uguale a quello della circonferenza verde) nella direzione della freccia azzurra. Dopo un certo intervallo di tempo, O₁ si porta in O₁’, P si porta in P’ e le due circonferenze di partenza si toccano in H.

Per come avviene il movimento deve rimanere costante la distanza percorsa da P rispetto a H, ossia la distanza PH deve rimanere uguale a P’H.

Ciò che vogliamo dimostrare è che il punto P (pallino verde) si muove lungo il diametro QP della circonferenza grande, ossia percorre un segmento rettilineo da P fino a Q e viceversa, durante il rotolamento completo della circonferenza verde all’interno di quella nera (ovviamente, se il raggio di una è la metà di quella dell’altra).

Per arrivare a questo risultato basta dimostrare che l’angolo POH è uguale a P’OH (non fatevi ingannare dalla figura, che ovviamente deve mettere il punto nella giusta posizione… P’ potrebbe teoricamente essere in una posizione diversa). La tesi è quindi:

POH = P’OH

Cominciamo a notare che l’angolo P’OH è la metà dell’angolo P’O₁’H, dato che il primo è l’angolo alla circonferenza e il secondo è l’angolo al centro dello stesso arco P’H della circonferenza verde di centro O1’

P’O₁’H = 2 P’OH              …. (1)

Sappiamo, però, che gli archi PH e P’H sono uguali.  L’arco PH corrisponde all’angolo POH della circonferenza nera, mentre l’arco P’H corrisponde all’angolo PO₁’H della circonferenza verde. In parole povere, abbiamo trovato che due archi sono uguali e corrispondono ad angoli al centro di circonferenze che hanno una il raggio doppio dell’altra. Questo non può che significare che gli angoli sono uno la metà dell’altro (o viceversa)!

Possiamo scrivere:

P’O₁’H = 2 POH               …. (2)

Dalla (1) e dalla (2) si ottiene subito:

P’O₁’H = 2 P’OH = 2 POH

P’OH =  POH

Come volevasi dimostrare.

L’importanza storica e “scientifica” è enorme, dato che si è in realtà distrutta la convinzione tolemaica e i movimenti circolari tipici del Cosmo riescono, combinandosi, a produrre un movimento “terrestre” rettilineo e nemmeno uniforme.

Tuttavia, il teorema di Copernico o di Al-Tusi (come preferite), comporta la possibilità di descrivere una traiettoria ellittica. Invece di considerare il moto di un punto sulla circonferenza minore, consideriamo il moto di un punto interno alla circonferenza, ma che sia solidale con essa. Bene, provate a disegnarlo e vedrete che esso descrive un’ellisse! Siamo ancora ben lontani da Keplero, ma le basi erano già state gettate…

Riportiamo più correttamente l’enunciato: se un cerchio minore rotola all'interno di un cerchio maggiore con diametro doppio, allora il luogo geometrico di un punto che non giace sulla circonferenza del cerchio minore, ma che è fisso rispetto a questo cerchio minore, costituisce un'ellisse.

Le due circonferenze ci permettono, inoltre, di fare un bel giochino con tante palline (non quelle di Pippo e Pappo). Facendo rotolare la nostra circonferenza minore e facendo partire varie palline in corrispondenza di diversi punti di contatto con la maggiore (in pratica, le palline partono in ritardo una rispetto all’altra), esse descrivono diametri diversi della circonferenza maggiore. Guardando soltanto le palline, sembra di vedere una strana ruota che rotola attorno al cerchio. Si crea l’illusione che le palline tutto facciano meno che descrivere, ognuna, una traiettoria rettilinea.

Meglio di tante parole vale il video che segue…

Che dire, la geometria sa essere molto simpatica e divertente, anche quando ha tanti secoli sulle sue spalle.