Per una trattazione organica dell'argomento "Velocità della Luce" si rimanda alla relativa pagina d'archivio, nella quale è stato inserito anche questo articolo

 

Questo articolo recupera vecchi articoli e quiz e presenta alcuni fenomeni  che fanno  apparire velocità superiori a quella della luce. Non parliamo di tachioni o di neutrini o di entanglement, ma di qualcosa alla portata di chiunque. In particolare, ci dedichiamo a qualcosa che è proprio l'opposto della luce: l'ombra!

Sappiamo molto bene che niente o nessuno può andare più veloce della luce e solo i fotoni, privi di massa, possono tranquillamente raggiungerla. Anzi, sono obbligati a farlo se no non sarebbero più fotoni...  Oggi sappiamo che, probabilmente, anche le onde gravitazionali viaggiamo alla stessa velocità. Poi si può anche sconfinare in tante altre ipotesi come quelle che riguardano i tachioni e gli stessi neutrini. Per non parlare, poi, dell'effetto quantistico chiamato "entanglement",  rispetto a cui la velocità della luce sembrerebbe quella di una vera tartaruga...

Tuttavia, in questo articolo, vogliamo solo parlare di effetti, più o meno apparenti, che sembrano dimostrare la possibilità di superarla, pur rimanendo nelle condizioni "normali", quelle di tutti i giorni, sia utilizzando un telescopio sia anche solo il nostro occhio. Sappiamo che la lentezza della luce gioca molti scherzi, mettendo anche in crisi gli effetti della relatività ristretta, ma non vi è bisogno di andare molto distanti per trovar qualcosa che sembra superarla anche abbondantemente.

Effetti superluminali astronomici

Iniziamo dalla parte più generale, e probabilmente più semplice, ossia dai cosiddetti fenomeni superluminali, quelli in cui le velocità misurate di certi “oggetti”  celesti raggiungono valori anche notevolmente superiori a quella della luce.

Anche se la soluzione appare, adesso, abbastanza ovvia (un problemino di geometria), non possiamo dimenticare come queste osservazioni “apparentemente assurde”  abbiano creato non pochi problemi agli astrofisici.

1. Descrizione qualitativa

Questi fenomeni prendono il nome di sorgenti superluminali, in quanto sembrano propagarsi a velocità di gran lunga superiori a quella della luce. Normalmente sono associati a galassie attive e si formano a causa della caduta di materiale verso il buco nero centrale. Si presentano normalmente come getti di particelle che vengono scagliate verso lo spazio. Al loro interno si notano “nodi” più densi e luminosi che permettono di misurarne la velocità, dato che sono segni che possono essere seguiti col telescopio durante un periodo relativamente breve. Misurando lo spazio percorso da questi nell’unità di tempo si determina la velocità della materia del getto. Questo semplice “calcolo” può portare a velocità nettamente superiori a quella della luce, da cui il nome di sorgenti superluminali.

Questi valori assurdi per la fisica odierna derivano da un fenomeno prospettico non molto difficile da descrivere, che si può spiegare in modo semplificato e abbastanza intuitivo…

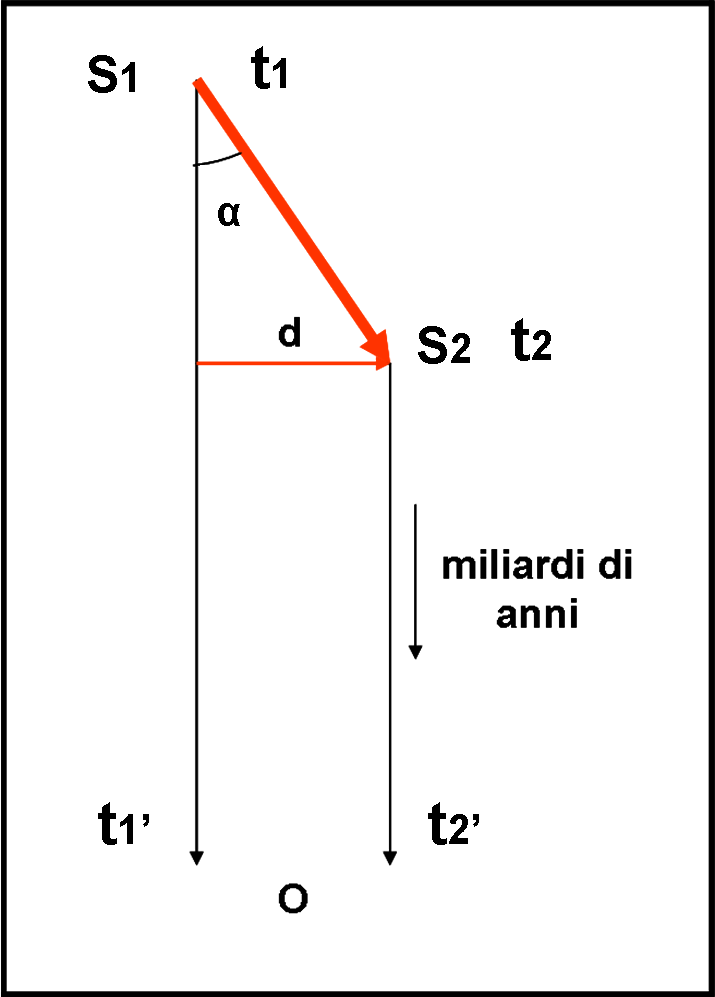
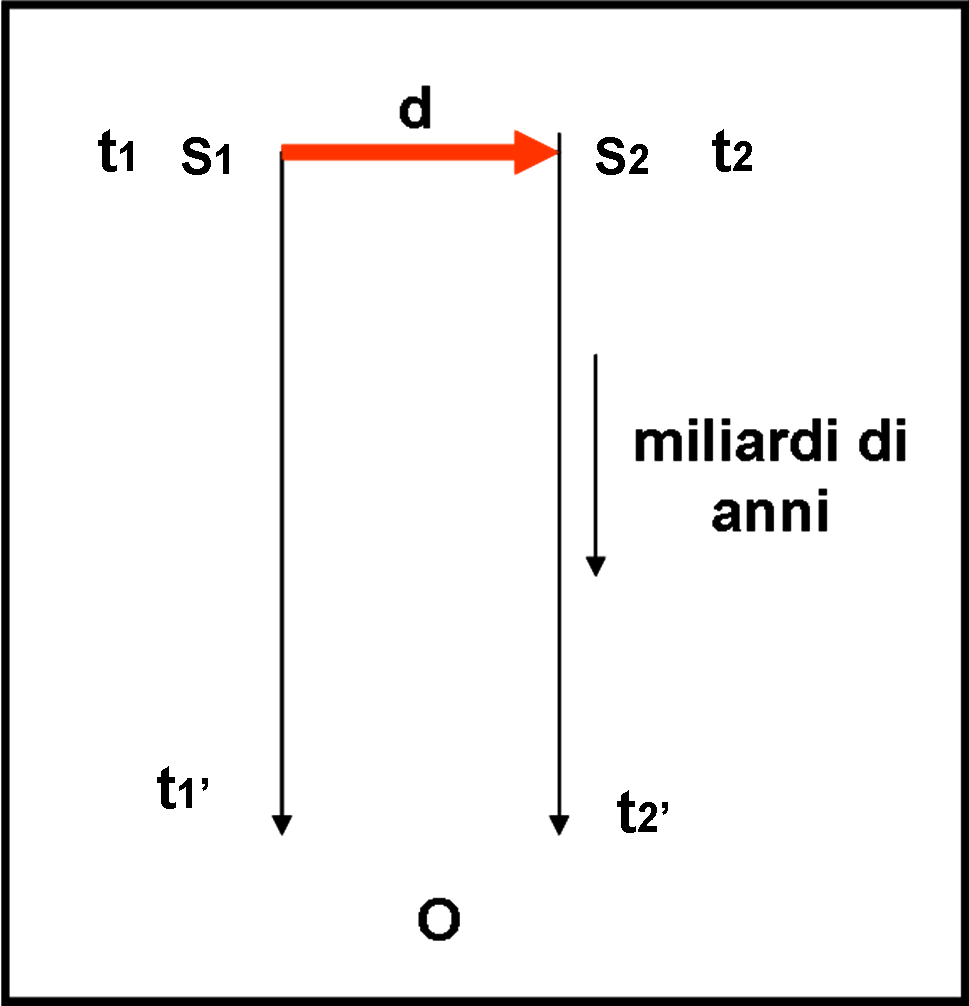
Consideriamo la Fig.1 in cui S₁ è  la sorgente all'interno del getto. Ammettiamo, per adesso, che la direzione del getto sia esattamente trasversale rispetto all’osservatore. Al tempo t₁’ osservo la luce del nodo partita al tempo t₁ (la differenza tra questi tempi dipende ovviamente dalla distanza della sorgente da noi e potrebbe anche essere di miliardi di anni, ma  poco importa). Al tempo t₂ il nodo si è spostato in S₂ e la sua luce giunge sulla Terra al tempo t₂’. Per percorrere il tratto S₁S₂ = d  nel tempo t₂ – t₁ il nodo ha viaggiato al velocità v = d/(t₂ – t₁). Questa è la velocità reale del getto e non può ovviamente superare quella della luce. Tuttavia, le si avvicina molto e questo è estremamente importante.

L’osservatore misura, ovviamente, la differenza di tempo (t₂’- t₁’) e la distanza d. Nella situazione rappresentata nella Fig. 1, la differenza t₂’ – t₁’ risulta perfettamente uguale a t₂ – t₁. Notiamo che per i valori estremamente piccoli dell’intervallo di tempo e della distanza percorsa possiamo trascurare completamente gli effetti dovuti all’espansione dell’Universo (lo spazio si espande ma non i singoli oggetti e il getto può considerarsi proprio come un singolo oggetto).

Se vogliamo calcolare la velocità osservata da terra dobbiamo fare v’ = d/(t₂’- t₁’), che è uguale a quella vera v = d/(t₂ – t₁), dato che t₂ – t₁ = t₂’- t₁’. La velocità misurata è altissima ma non va contro la teoria della relatività.

Non siamo, pero, sempre così fortunati… Consideriamo la Fig. 2, dove il getto è inclinato e forma un angolo α, abbastanza piccolo, con la linea di vista. Noi, ovviamente, non possiamo sapere la configurazione effettiva della sorgente e del suo getto e dobbiamo limitarci a eseguire i calcoli basandoci su quello che vediamo, che, in questo caso, è una proiezione,  sulla sfera celeste, di quanto capita realmente . Possiamo, oltretutto, calcolare solo i tempi di arrivo sulla Terra della luce del nodo durante il suo percorso.

La distanza d misurata è esattamente uguale a quella precedente (anche se non possiamo sapere se è una proiezione o è quella effettiva). Misuriamo nuovamente la differenza osservata tra i tempi  t₂’ e t₁’. Con grande meraviglia troviamo che  v = d/(t₂’– t₁’) supera di gran lunga la velocità della luce.

Dov’è l’errore?

Stiamo bene attenti… il calcolo che abbiamo fatto presuppone che le condizioni effettive siano come quelle del caso fortunato della Fig.1. D’altra parte, da terra, non possiamo fare altro. Siamo, quindi, costretti a considerare t₂’– t₁’ uguale a t₂ – t₁, ossia a considerare la differenza di tempo tra S₂ e S₁ come nel caso precedente.  E qui commettiamo l’errore fondamentale.

La differenza effettiva di tempo tra gli eventi REALI  S₂ e S₁ è ben maggiore di t₂’ – t₁’. Infatti, la luce che è arrivata da noi al tempo t₁’, relativa alla sorgente in S₁, è partita ben prima (t1) di quanto rappresentato in Fig. 1. Essa ha dovuto percorrere un tratto decisamente più lungo rispetto a quella che ha percorso S₂. Per trovare la vera velocità del getto dovremmo dividere la distanza per un tempo molto più lungo (che non possiamo conoscere).

Siamo, perciò, costretti a dividere per un valore più piccolo, che rispetto a quello vero decresce al diminuire dell’angolo α. Dividendo una distanza costante per un tempo sempre più corto rispetto a quello effettivo, troviamo una velocità sempre più grande che può tranquillamente superare di molto quella della luce, dato che la velocità reale è solo di poco inferiore.

2. Descrizione quantitativa

Supponiamo che dal buco nero BN venga emesso un getto di particelle verso l’osservatore lungo una direzione che forma un angolo α con la linea di vista (Fig. 3). Supponiamo inoltre che il nodo, visibile, si muova con una velocità v,  vicina alla velocità della luce c .

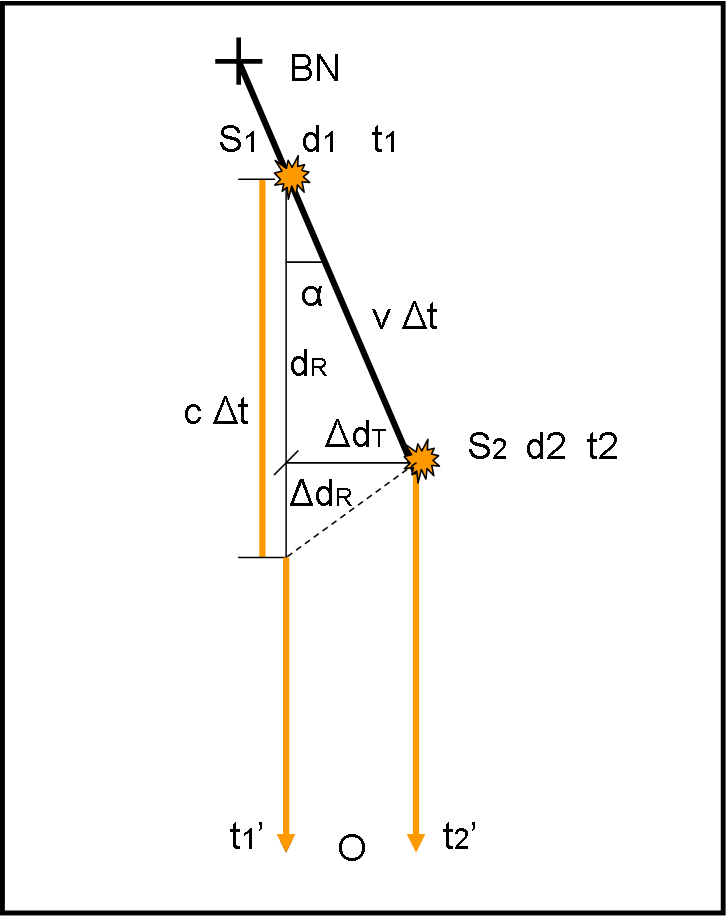
Siano d₁ e d₂ = d₁+ Δd = d₁ + vΔt, le distanze delle posizioni S₁ e S₂ del nodo rispetto al buco nero BN in due istanti  t₁ e t₂ = t₁ + Δt, rispettivamente. In queste due posizioni il nodo emette la propria luce. Nel passare da S₁ a S₂ , il nodo si avvicina all’osservatore, per effetto della sua velocità, di una quantità:

d_R = v cos(α) Δt

La luce emessa in direzione dell’osservatore quando era in S₁ ha già compiuto nel frattempo un tratto più lungo, pari c Δt .  Esiste, quindi, una differenza tra il tragitto percorso dalla luce verso di noi e quello percorso dal nodo. Quando il nodo arriva in S₂, ed emette la sua luce, quella inviata da S₁ è più a vicina a noi (c > v). La loro differenza spaziale, nella nostra direzione, è data da:

Δd_R = cΔt - v cos(α) Δt

Definendo la solita variabile β = v/c (la conosciamo bene…), i due impulsi luminosi, quello emesso in S₁ e quello emesso in S₂, viaggiano verso di noi, a una distanza costante, l’uno dall’altro, uguale a:

Δd_R = c (1- β cos(α)) Δt

e giungono distanziati da un tempo, decisamente più corto di quello realmente passato dall’emissione da parte di S1 e di S2:

Δt' = Δd_R/c = (1- β cos(α)) Δt .

Lo spostamento compiuto dal nodo in direzione ortogonale alla linea di vista, ovvero lo spostamento sulla sfera celeste, che è quello effettivamente misurato nel passaggio da S₁ a S_2, è dato da:

Δd_T = v sin(α) Δt .

Ne segue che la velocità del getto misurata da terra in questa direzione è pari a:

v' = Δd_T /Δt' ,

ovvero

v' = c (β sen (α))/(1- β cos(α)).

Se il getto si muovesse proprio lungo una direzione ortogonale alla linea di vista (caso fortunato della trattazione qualitativa), si avrebbe:

α = π/2

sin(α) = 1

cos(α) = 0

e, quindi:

v' = v.

La velocità osservata sarebbe effettivamente quella con cui si sposta il nodo. Per un getto diretto verso l’osservatore la velocità apparente può, invece, superare nettamente quella della luce.

Volendo, si possono determinare i valori di v’ per vari valori di β e per vari valori di α. Un esercizio niente male… che dimostra che si ottengono velocità apparenti maggiori di quella della luce solo per valori di β molto prossimi a 1 e per angoli α minori di 90°.

L'ombra

La prima parte può essere anche prospettata come un semplice quiz, una specie di indovinello, alla cui risposta si può arrivare con un lampo di intuito. La seconda parte è decisamente più difficoltosa, anche se fa solo uso di una matematica e di una geometria elementari…

Tutte le sere sotto quel lampione...

Abbiamo un lampione che ha un’altezza L. Davanti a lui vi è una persona che è alta h (< L). La distanza tra il lampione e la persona è uguale a d. la lunghezza dell’ombra proiettata dalla persona è s.

Per un qualsiasi piccolo allontanamento della persona rispetto al lampione, l’ombra si allunga con una certa velocità. La domanda è: “Si muove più velocemente l’ombra di una persona alta o di una bassa (posta, ovviamente, alla stessa distanza dal lampione)?”

La figura relativa all’ombra di una persona che si sposta rispetto a un lampione è molto semplice (Fig. 4).

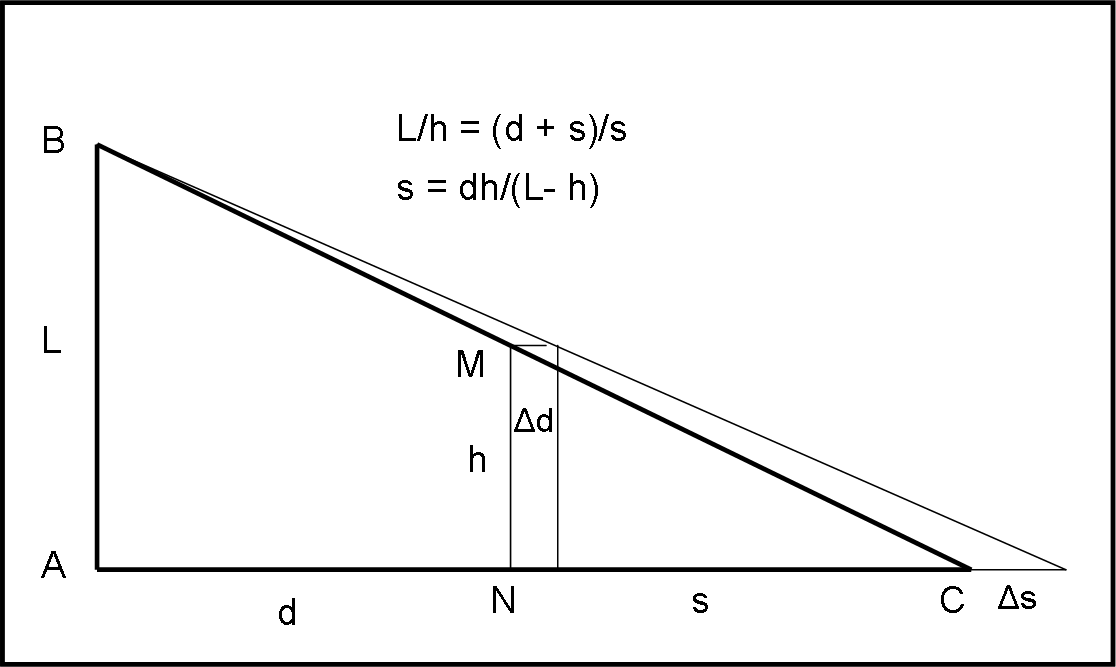
Dai triangoli simili ABC e MNC, si ha:

AB/MN = AC/NC

L/h = (d + s)/s

sL =h(d + s)

sL – hs = hd

s = hd/(L – h)

Sappiamo che h ed L sono costanti. Possiamo scrivere:

s = (h/(L - h)) d

Se la persona si sposta in avanti, aumenta il valore di d. Aumentando d, varia s che è funzione della sola d.

Per uno spostamento Δd, abbiamo:

Δs =  (h/(L – h)) Δd

Dividendo entrambi i membri per il corrispondente intervallo di tempo Δt, necessario a ottenere Δd (e Δs), otteniamo il confronto tra la velocità della persona v_P (variazione di d) e la velocità dell’ombra v_O (variazione di s)

Δs/Δt = (h/(L – h)) Δd/Δt

v_O = (h/(L – h)) v_P

Se la persona è più bassa, cambia la sua altezza h, ma non cambia la sua velocità di spostamento, cioè v_P. La velocità v_O della persona più bassa dipende, perciò, solo dal coefficiente (h/(L – h)). Se diminuisce h, diminuisce il numeratore e cresce il denominatore (L > h).

Ne segue che diminuisce il valore del coefficiente e quindi anche la velocità dell’ombra.

Possiamo fare anche una rapida prova pratica. Ammettiamo che h passi da 1.80 a 1.50 m. Il lampione sia alto 4 m. Nel primo caso, abbiamo:

1.8/(4 – 1.8) = 0.818

Nel secondo caso, abbiamo:

1.5/(4 – 1.5) = 0.60

v_O(alto) = 0.818 v_P

v_O(basso) = 0.60 v_P

Ricavando v_P e uguagliando, si ha:

v_O(alto)/0.818 = v_O(basso)/0.60

v_O(basso) = (0.60/0.818) v_O(alto)

v_O(basso) = 0.73 v_O(alto)

Come volevasi dimostrare.

Ammettendo che le persone si muovano di moto uniforme abbiamo fatto a meno di eseguire le derivate e ci è bastato fare le divisioni tra intervallo di spazio e intervallo di tempo (ma sarebbe cambiato ben poco).

Abbiamo anche considerato l’intervallo di tempo dell’ombra uguale a quello della persona, ossia abbiamo considerato istantaneo l’arrivo della luce ai limiti dell’ombra. Questa semplificazione porta a risultati inaspettati e imprevedibili.

Vediamo di dimostrarlo con un semplice esperimento geometrico.

Uno schermo che si abbassa

Consideriamo la Fig. 5.

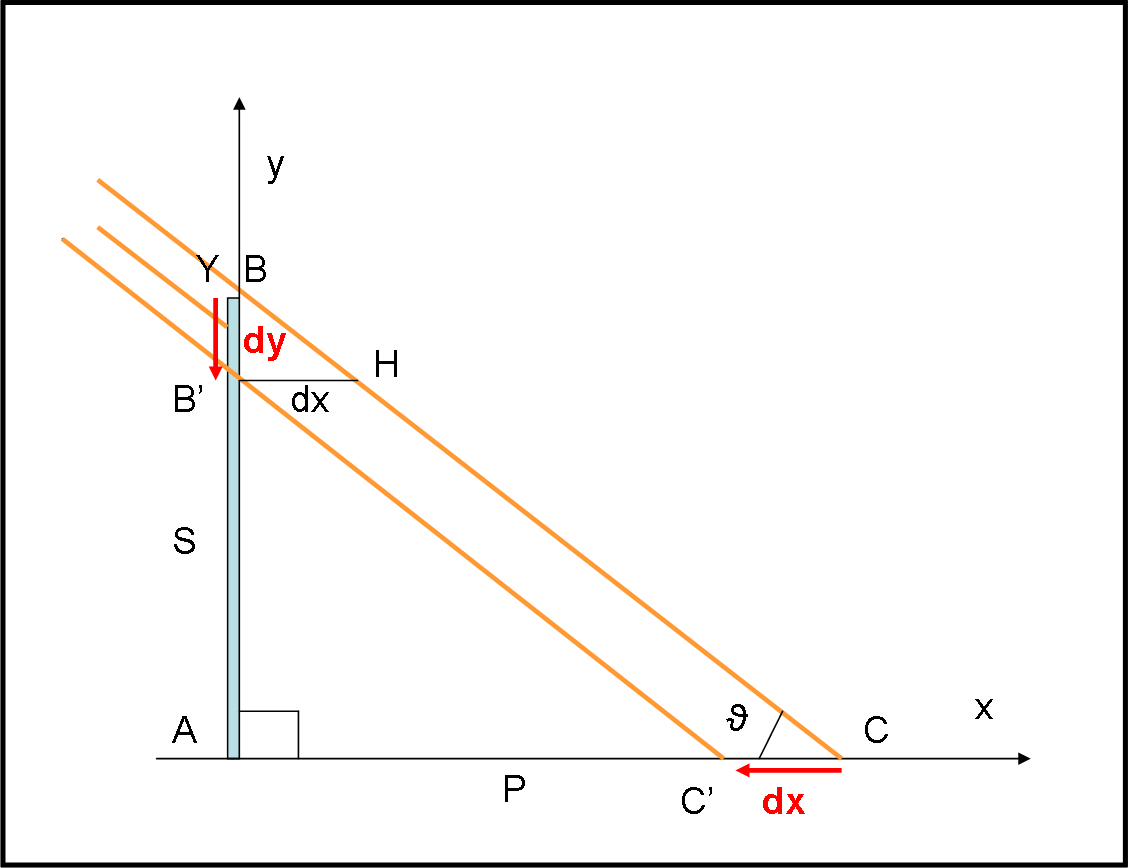
A sinistra vi è uno schermo S che può abbassarsi alla velocità che vogliamo. Esso viene investito da un fascio luminoso i cui raggi sono paralleli tra loro (sorgente molto lontana). L’ombra relativa allo schermo S si allunga sul pavimento P. Poniamo l’asse x lungo il pavimento e l’asse y lungo lo schermo. Schermo e pavimento sono perfettamente perpendicolari tra loro. Immaginiamo una situazione statica. Il primo raggio che oltrepassa lo schermo sfiora il punto B e giunge in C. L’ombra copre esattamente la linea AC. Sia, inoltre, BCA = ϑ l’angolo di inclinazione dei raggi rispetto al pavimento.

Scriviamo una semplice relazione tra i cateti del triangolo rettangolo BAC:

BA/AC = tan(ϑ)

Chiamiamo BA = Y e AC = X

Y/X = tan(ϑ)

Ricaviamo la lunghezza dell’ombra in funzione dell’altezza dello schermo:

X = Y/tan(ϑ) = Y cot(ϑ)

Abbiamo soltanto richiamato la funzione cotangente (QUI) che altro non è che l’inverso della tangente o, se preferite, il rapporto coseno/seno. Per semplicità chiamiamola solo cot e non cotan

Per adesso abbiamo fatto un confronto tra lunghezze…

Passiamo adesso al calcolo delle velocità. Abbassiamo lo schermo di una quantità dy (BB’). Ne segue che anche l’ombra si accorcia e il suo punto estremo passa da C ad C’, ossia percorre uno spazio dx. I triangoli ABC e BB’H sono ovviamente simili e vale immediatamente la relazione:

dx = dy cot(ϑ)

Ricordiamoci, adesso, una vera banalità: la velocità è data dal rapporto tra lo spazio percorso e il tempo impiegato a percorrerlo.

Noi sappiamo perfettamente quanto vale la velocità di abbassamento dello schermo v_S. Essa è data da:

v_S = dy/dt

Analogamente si può calcolare la velocità dell’ombra v_O:

v_O = dx/dt = dy cot(ϑ)/dt = v_S cot(ϑ)

Come abbiamo detto precedentemente, la velocità di abbassamento dello schermo può essere scelta a piacere. Per non fare torto ad Einstein (un pochino sì perché ha una massa…), immaginiamo di abbassarlo alla velocità della luce (ma potremmo anche abbassarlo a una velocità di poco inferiore… e sarebbe più contento).

La relazione precedente si riduce (ponendo v_S = c = 1) a:

v_O = cot(ϑ)

Non ci resta che fare qualche conto o, ancora meglio, disegnare, in un grafico, v_O in funzione dell’angolo ϑ, che può variare tra 0° e 90°, per costruzione. Vediamo, perciò, in Fig. 6, come varia v_O in funzione dell’angolo di inclinazione dei raggi, avendo posto c = 1.

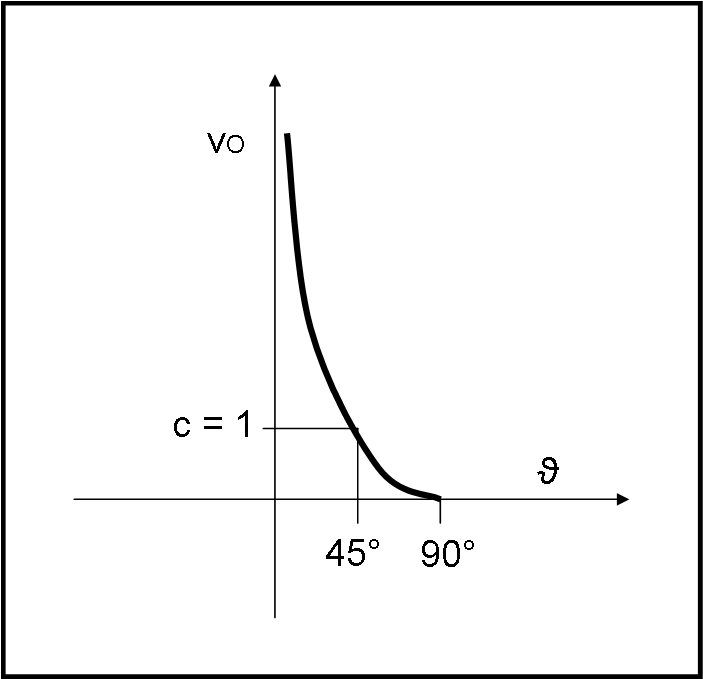
Non è difficile concludere che per valori di ϑ inferiori a 45° la cotangente è maggiore di 1 e quindi la velocità dell’ombra supera la velocità della luce. Addirittura tende a infinito (singolarità!) per ϑ che tende a zero (ombra estremamente radente).

Per capire il perché, basta disegnare in Fig. 7, il sistema “schermo - luce - pavimento” con angoli diversi. Se l’angolo è minore di 45°, l’ombra supera lo scorrimento dello schermo. Se l’angolo è maggiore di 45,° l’ombra diventa più piccola, fino a diventare ZERO per un angolo di 90° (chiedete ad Eratostene e ai suoi pozzi…). L’ombra tende, invece, a infinito per angoli vicini a zero.

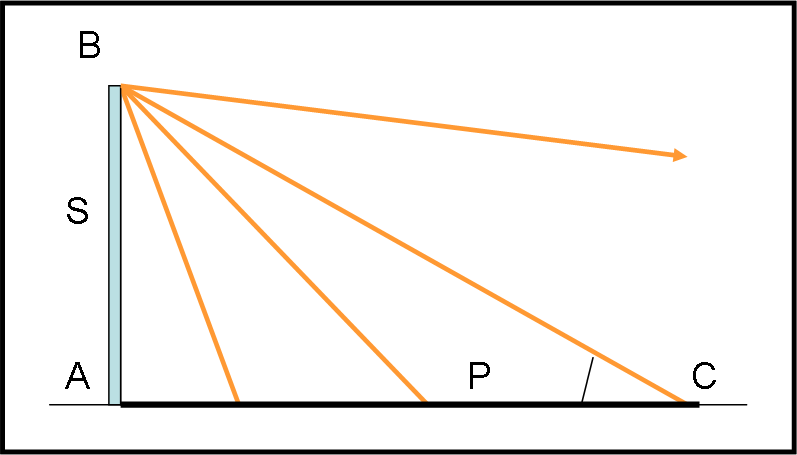
In realtà, se i raggi diventano quasi paralleli al pavimento sembra proprio che l’ombra si proietti (potendola vedere) attraverso l’intera galassia, e anche oltre, in un attimo. Quasi meglio che le particelle “entangled”.

Tuttavia, prima di andare avanti, rileggiamo bene quanto è stato scritto fin qui… Abbiamo fatto un ERRORE MADORNALE. Va subito corretto. Il bello è, però, che anche correggendolo, il risultato non cambia di molto e se ne vedranno delle belle…

Ammettendo che lo scorrimento dello schermo possa avvenire a velocità prossime a quelle della luce, l’errore più grosso che abbiamo fatto  è stato quello di trascurare del tutto il tempo che la luce impiega a percorrere spazi diversi. Nel caso della persona più alta o più bassa potevamo benissimo supporre che l’arrivo della luce fosse istantanea sui due individui, sia relativamente alla loro altezza che al loro piccolo movimento in avanti, la stessa cosa non può più essere fatta nel caso che lo scorrimento avvenga a velocità molto alte.

Prima di passare a qualche formula, cerchiamo di capire il concetto essenziale dell’esperimento e perché esso abbia senso solo facendo scorrere verso il basso lo schermo. Innanzitutto, per non mettere troppa carne al fuoco, limitiamo il nostro problema a una sola variabile: la velocità di scorrimento dello schermo v_S. L’altra variabile, l’angolo di incidenza dei raggi luminosi, ϑ, lo manteniamo fisso, ossia diventa una costante.

Immaginiamo, inoltre, che la luce venga inviata attraverso raggi luminosi (cosa usata comunemente e non errata concettualmente), intervallati da infinitesimi intervalli di tempo. Intervalli di tempo che definiscono la velocità v_S, data dalla lunghezza dello scorrimento infinitesimo diviso per il tempo che intercorre tra due raggi. In altre parole, dopo la partenza di un raggio luminoso, lo scorrimento deve essere  ds e il tempo trascorso dt, prima che parta il raggio successivo. Costruiamo, perciò, una specie di cannone a luce, che spari con una certa velocità i suoi proiettili-raggi.

Il cannone a luce è lo schermo che scende di una quantità  ds ogni dt  prima di inviare il suo raggio. I raggi sono quindi paralleli tra loro (ϑ non cambia) e sono intervallati da uno stesso spazio e da uno stesso tempo. Abbiamo già capito un concetto fondamentale: quando passeremo a trattare la velocità dell’ombra proiettata sul pavimento, non studieremo effettivamente ciò che capita all’ombra, ma analizzeremo l’arrivo dei raggi luminosi sul pavimento. Il bordo estremo dell’ombra, ossia la sua apparente velocità, non è altro che la velocità con cui i raggi di luce giungono sul pavimento, causando una variazione della lunghezza dell’ombra e, quindi, una sua apparente velocità di scorrimento. Questo fatto ci dice una cosa importantissima: l’informazione sul movimento dell’ombra e l’apparente velocità di quest’ultima, viaggia solo e soltanto alla velocità della luce e quindi Einstein può dormire sonni tranquilli.

Torniamo al nostro “cannone” di Fig. 8.

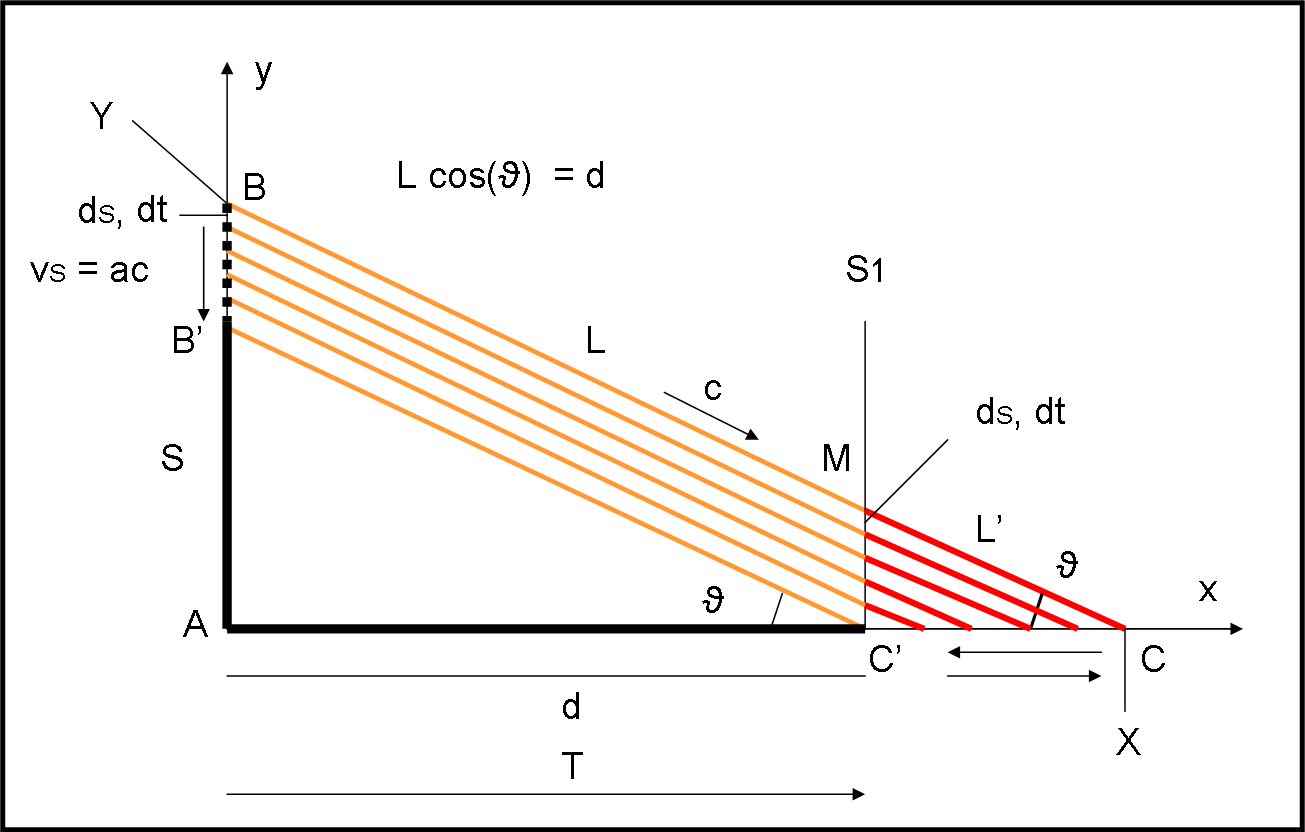
Poniamo un altro schermo S₁ FISSO parallelo al primo. Ogni raggio di luce sparato dal primo schermo colpisce il secondo schermo dopo un certo tempo T, legato alla velocità della luce c e alla distanza L che è poi nient’altro che d/cosϑ. Il tempo T è quindi una costante (come è ovvio anche intuitivamente) e possiamo concludere che lo schermo S₁ non fa altro che ripetere ciò che capita in S, con un ritardo di tempo costante, uguale a T. In altre parole, la luce si è trasferita in S₁ con le stesse modalità che aveva alla partenza da S. Per potere illuminare l’ombra del pavimento (ossia farla muovere) è, però, necessario che ogni raggio colpisca il pavimento.

Diventa, perciò fondamentale il tragitto che ogni raggio compie per andare da S₁ al pavimento. E qui le cose cambiano radicalmente: il raggio più alto arriva per primo su S₁, ma poi impiega un tempo, che è più lungo rispetto a quello del raggio successivo, per giungere sul pavimento in C. L’ultimo raggio arriva sicuramente dopo, ma quando arriva in  S₁ è anche arrivato sul pavimento, in C’.

Ne segue, da un punto di vista intuitivo, che siamo di fronte a un confronto di tempi: Il tempo che il cannone impiega a sparare i suoi proiettili-raggi (dt) e quello necessario a percorrere il tragitto L’ che è funzione dell’angolo ϑ e che varia da raggio a raggio.

Il triangolo MC’C è il triangolo fondamentale per ogni nostro calcolo. Se il cannone spara lentamente, il primo raggio ha tutto il tempo di arrivare in C, prima che arrivi il secondo raggio e via di seguito. La luce illumina l’ombra e sposta il suo bordo estremo andando da destra verso sinistra, come è logico aspettarsi. Prima la luce arriva in C, per finire poi in C’.

Ma, se il cannone spara molto velocemente, può capitare che il raggio diretto in C’ arrivi addirittura prima di quello diretto in C. In altre parole, se il cannone spara a raffica, il tempo intercorso dal primo all’ultimo raggio sparato, può essere decisamente minore del tempo che il primo raggio impiega per passare da M a C! La luce illumina l’ombra in senso inverso! Prima illumina C’ e poi, per ultimo, proprio C.

Anche se rischiamo di ripeterci, analizziamo ancora meglio, in Fig. 9, questa situazione dall’apparenza assurda, partendo dall’invio della luce dallo schermo S. Trattiamo i raggi di luce proprio come fossero colpi di cannone, scegliendo i tempi degli spari.

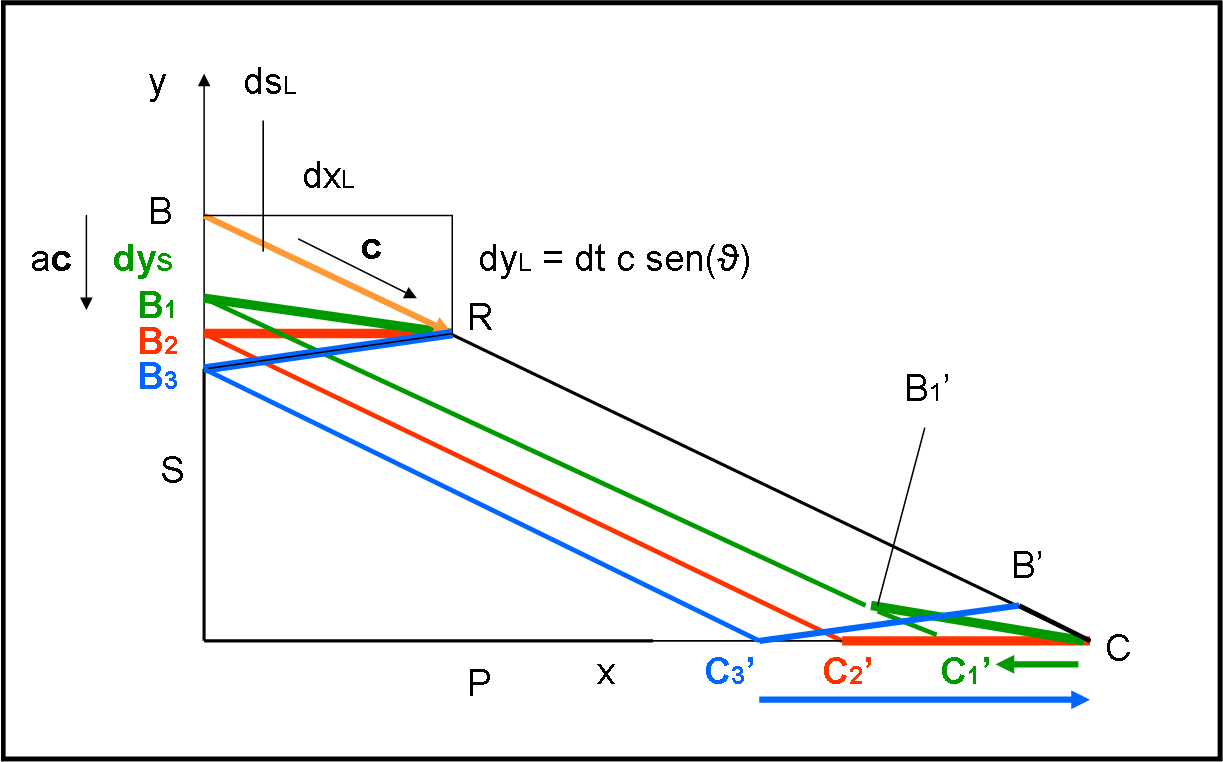
Facciamo partire il primo raggio di luce che viaggia verso il pavimento P con una velocità c. Immaginiamo di bloccarlo nel punto R dopo un intervallo di tempo dt.

Risulta:

ds_L = dt c

ds_L  può essere scomposto nelle sue due componenti dx_L e dy_L che valgono:

dx_L = dt c cos(ϑ)

dy_L = dt c sen(ϑ)

Occupiamoci soltanto della componente verticale.

Nel momento in cui la luce (il primo proiettile) ha raggiunto il punto R, dopo un tempo dt, lo schermo è sceso fino a B₁, di una certa quantità dy_S, che dipende dalla sua velocità v_S = ac, con a, ovviamente, minore di 1 (se no Einstein si arrabbia troppo!).

Ne segue che

BB₁ = dy_S =  dt a c.

In quel preciso momento spariamo il secondo raggio di luce.

Siamo nelle condizioni in cui:

BB₁ =  dt a c < dt c sen(ϑ)

Ossia:

a < sen(ϑ)

Qual è il “fronte d’onda” dei due raggi luminosi considerati finora (ossia la linea che unisce i loro punti più avanzati al tempo dt)? Beh… il primo è arrivato in R il secondo è ancora in B₁. Ne segue che esso è rappresentato dalla linea verde B₁R.

A questo punto, il fronte d’onda, ossia la linea verde, può solo spostarsi alla velocità della luce fino a che il raggio partito da B tocchi il pavimento in C. B₁’, il corrispondente di B₁, è ancora in viaggio e, di conseguenza, tocca il pavimento in ritardo rispetto al primo raggio. Come conseguenza, l’ombra sparisce da C e solo dopo sparisce anche da C₁’. L’apparenza del fenomeno è, quindi, quella che mostra il limite dell’ombra che si sposta da C verso C₁’, con una certa velocità (proprio quella che indichiamo come velocità dell’ombra v_O).

Ribadiamo il concetto fondamentale: l’ombra appare muoversi da C verso C₁’ dato che la luce arriva prima in C e poi in C₁’. Calcoleremo in seguito con esattezza la velocità di questa “ombra”. Per ora ci basta avere capito il verso che segue.

A questo punto cambiamo la velocità ac dello scorrimento dello schermo S. in particolare, aumentiamo a in modo tale che nel tempo dt lo schermo arrivi esattamente nel punto B₂. In quel momento spariamo il secondo raggio (rosso). Esso è stato scelto proprio in modo che:

BB₂ = dt a c = dt c sen(ϑ)

Ossia:

a = sen(ϑ)

Il fronte d’onda al tempo dt è, adesso, la linea orizzontale rossa B₂R, Essa viaggia alla velocità della luce e tocca contemporaneamente sia C che C₂’. L’ombra sparisce nello stesso momento sia da C che da C₂’ e appare viaggiare a una velocità infinita, dato che percorre l’intervallo CC₂’ in un tempo uguale a zero.

Passiamo al terzo caso, forse il più assurdo… Aumentiamo ancora la velocità di scorrimento dello schermo S, in modo che al tempo dt lo schermo sia arrivato in B₃. Come al solito, spariamo la nostra cannonata di luce. Siamo nelle condizioni in cui:

BB₃ = dt a c > dt c sen(ϑ)

Ossia:

a > sen(ϑ)

Il fronte d’onda è la linea blu B₃R. Essa prosegue alla velocità della luce, ma il primo punto che tocca il pavimento P è, adesso, il punto C₃’, corrispondente al raggio partito per secondo. Il primo raggio è ancora in B’, con un certo ritardo corrispondente al tempo che B’ impiega per giungere in C. Ne consegue che la luce arriva prima in C₃’ e solo dopo in C. L’ombra appare muoversi da C₃’ verso C, in verso opposto a quello del primo caso trattato (verde).

E’ facile comprendere che se, invece di un cannone che spara a comando, usassimo una mitragliatrice che spara in modo continuo, come, in realtà, si comporta la luce mentre si abbassa lo schermo, tutto ciò che abbiamo detto si trasforma in un fenomeno continuo con l’ombra che sembra proprio muoversi in un verso o nell’altro.

Einstein non si arrabbia

Tuttavia, ripetiamo ancora, la luce, ossia l’informazione che decide chi si oscura per primo o per ultimo, viaggia sempre alla sua velocità c. E’ solo una questione di ritardi o di anticipi, causati da percorsi diversi che creano ciò che si vede sull’ombra “vagabonda” e velocissima. In ogni caso, però, è indubbio che possiamo assistere a un “qualcosa” di visibile e misurabile che riesce a superare la velocità della luce. Un qualcosa, però, che non ha niente di reale e concreto, come massa, energia, quantità di moto, ecc. Insomma, Einstein può dormire sonni tranquilli.

Vale la pena riassumere, ancora una volta, il meccanismo, in modo molto semplificato. L’ombra scorre da destra verso sinistra per a < sen (ϑ) e in senso contrario per a > sen (ϑ). Nel caso limite a = sen (ϑ), l’ombra scompare immediatamente in ogni punto e può dirsi che si muove a velocità infinita.

Per visualizzare direttamente ciò che capita nei tre casi, utilizziamo con vero piacere l’animazione di Fabrizio, che rende in modo perfetto quando discusso precedentemente.

Prima di passare alla descrizione leggermente più matematica, pensiamo un attimo al perché  abbiamo fatto scorrere lo schermo verso il basso. Non potevamo fare il contrario e farlo spostare verso l’alto? Sarebbe stata un’esperienza più vicina alla realtà di un ombra, che si muove a mano a mano che una certa zona non riceve più la luce.

E’ facile comprendere, guardando la Fig. 10, che se lo scorrimento fosse verso l’alto ogni raggio successivo (i colpi di cannone) non solo partirebbe in ritardo rispetto al primo, ma dovrebbe anche percorrere tragitti più lunghi.

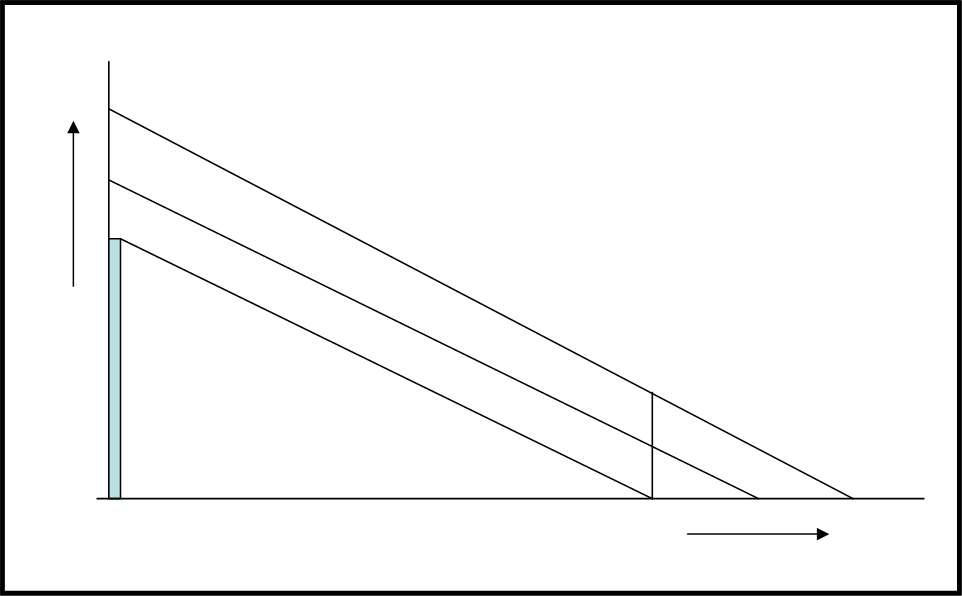
L’ombra, ossia la sparizione della luce, è costretta ad andare sempre nello stesso verso e la sua velocità rimane sempre inferiore a quella della luce, qualsiasi sia la velocità con cui si alza lo schermo. Questa situazione la vedremo meglio alla fine dell’articolo.

In viaggio con l’ombra: un po’ di matematica (semplice).

Per capire meglio tutte queste conclusioni QUALITATIVE è giunta l’ora di usare qualche formuletta e tornare alla prima versione (sbagliata) della soluzione sulla velocità dell’ombra.

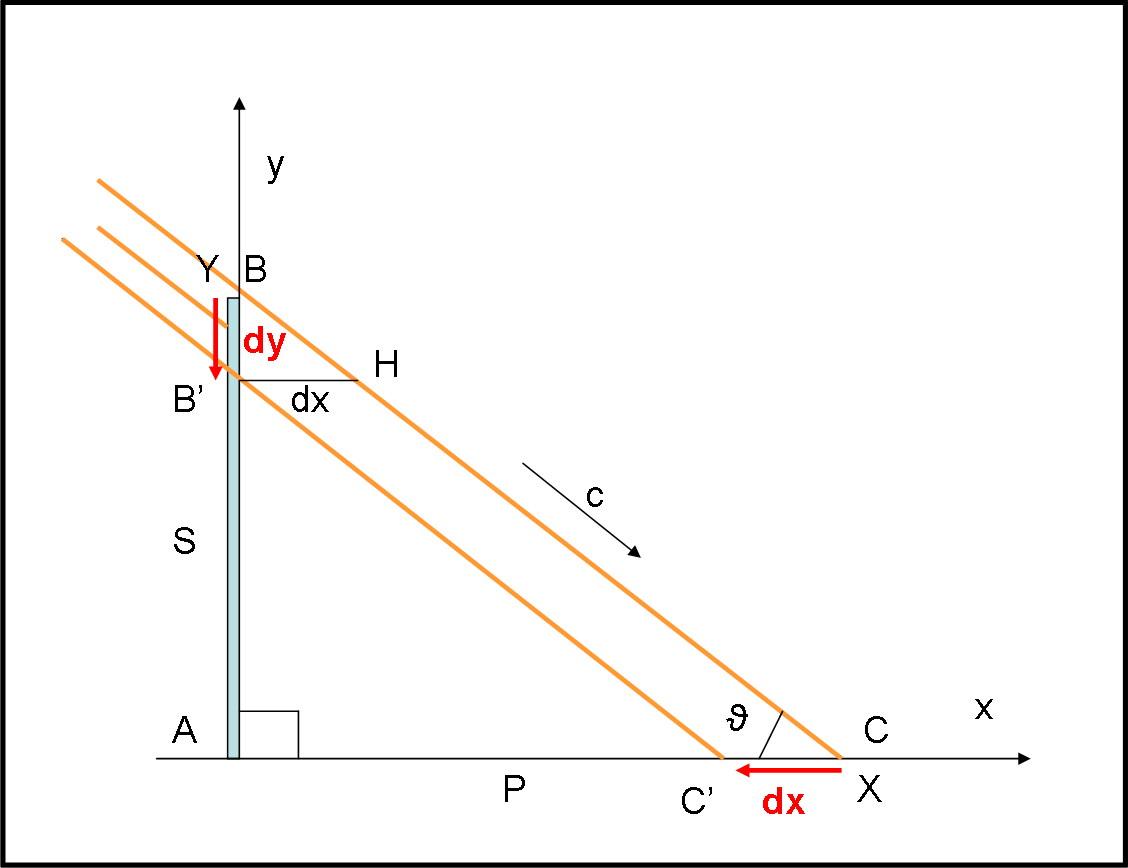
Analizziamo la Fig. 11 (che riporta nuovamente la Fig. 5), e ricordiamo quanto ottenuto:

dx = dy cot(ϑ)              …. (1)

v_O = dx/dt = dy cot(ϑ)/dt = v_S cot(ϑ)

Ne seguiva che, per certi valori dell’angolo ϑ, si superava abbondantemente la velocità della luce.  In particolare per tutti i valori per cui la cot(ϑ) era maggiore di 1. Per semplicità avevamo posto la velocità di scorrimento uguale a quella della luce, ma la situazione valeva anche per velocità v_S = ac, con a < 1.

Riscriviamo la relazione fondamentale:

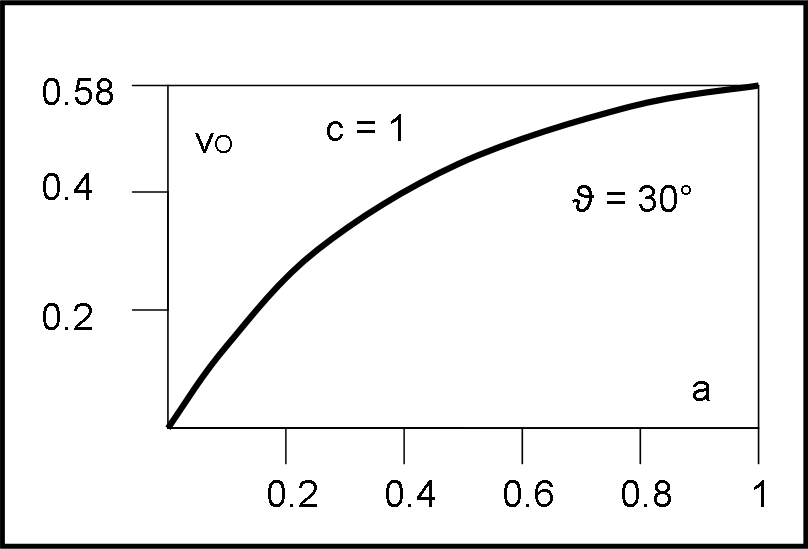
v_O = a c cot(ϑ)

Fissiamo un certo valore di ϑ e facciamo variare a, come fatto precedentemente.  A questo punto cot(ϑ) è una costante come c (che possiamo porre = 1). La relazione precedente non è altro che l’equazione di una retta che passa per l’origine nelle coordinate a e vo. La Fig. 12 mostra questa funzione per ϑ = 30°. E’ sufficiente una a = 0.58 per far viaggiare l’ombra alla velocità della luce.

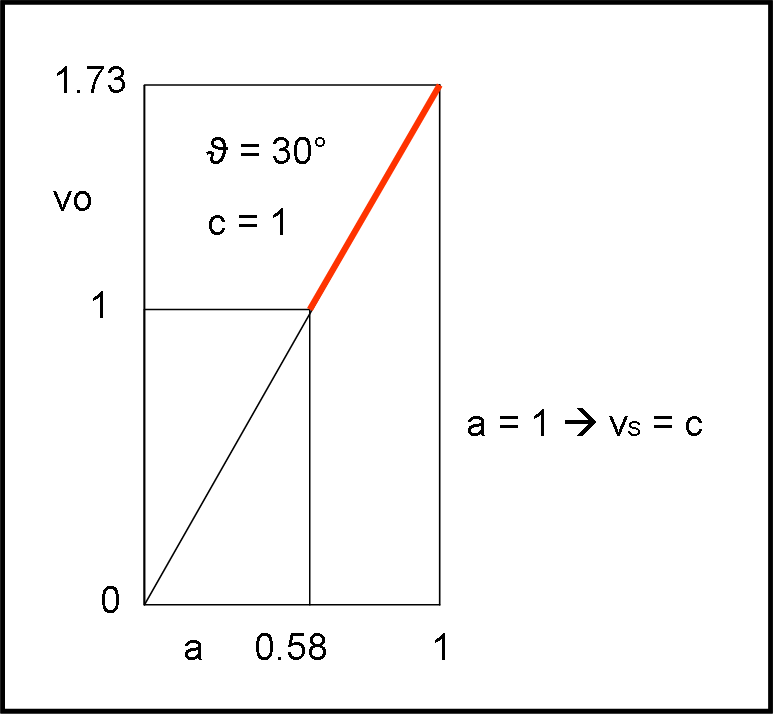
Tutte queste conclusioni sono, però, sbagliate, in quanto per ottenerle abbiamo usato lo stesso tempo dt sia per calcolare la velocità di scorrimento che la velocità dell’ombra. In altre parole, abbiamo diviso spazi diversi per lo stesso tempo e abbiamo ottenuto delle velocità. Il problema è che il tempo non è lo stesso e va calcolato quello corrispondente allo spazio percorso dall’ombra. Per far ciò dobbiamo analizzare attentamente i tempi di arrivo sul pavimento P dei raggi di luce, con i loro ritardi, perché solo la differenza tra questi ci dà l’intervallo di tempo giusto per il calcolo della velocità dell’ombra.

Continuiamo con la Fig. 11 e facciamo qualche ragionamento più attento e controllato. Qual è in realtà il tempo di inizio del movimento dell’ombra in C ? Non è certo quello in cui si lancia il primo raggio da B. la luce deve, infatti, arrivare fino a C e impiega un certo tempo. Abbiamo quindi un ritardo dell’inizio del movimento dell’ombra in C (ossia dell’arrivo della luce in C).

Il tratto che deve percorrere la luce è, perciò, BC che possiamo scrivere come:

BC = Y/sen(ϑ)

Il raggio si muove alla velocità della luce ed è quindi immediato scrivere l’intervallo di tempo dt₁ che la luce impiega per passare da B a C:

dt₁ = BC/c = Y/(c sen(ϑ))           …. (2)

Possiamo chiamare questo intervallo di tempo il ritardo dell’inizio del movimento dell’ombra rispetto all’inizio dello scorrimento dello schermo. Esso non è altro che il tempo impiegato dalla luce per passare da B a C.

Calcoliamo, adesso, il ritardo della fine del movimento dell’ombra. Infatti, l’ultimo raggio B’C’ impiega un certo tempo per percorrere il tragitto B’C’. Un tempo che NON è certo uguale a quello precedente, dato che lo spazio da percorrere è decisamente minore (B’C’ <  BC).

Chiamo questo secondo ritardo dt₂. Esso vale:

dt₂ = B’C’/c = (Y – dy)/(c sen(ϑ))          …. (3)

che, ripetendo, non è altri che il ritardo della fine del movimento dell’ombra rispetto alla fine dello scorrimento dello schermo (dy è la lunghezza dello scorrimento). In altre parole, è il tempo che la luce impiega per andare da B’ a C’.

Bene. Adesso abbiamo tutti i dati per calcolare l’effettivo tempo trascorso dall’inizio alla fine del movimento dell’ombra, ossia del tratto dx = CC’.

L’intervallo di tempo sarà dato dalla differenza tra il tempo finale e il tempo iniziale.

Poniamo come tempo d’inizio dell’intero esperimento t = 0. Ne segue che il tempo finale è dato da:

t_F = 0 + dt + dt₂        (dt è il tempo di scorrimento dello schermo)

Mentre il tempo iniziale è dato da:

t_I = 0 + dt₁

Basta effettuare la differenza e otteniamo l’intervallo di tempo  dt_O corrispondente allo spazio dx percorso dall’ombra.

dt_O = t_F – t_I =  dt + dt₂ – dt₁

Sostituendo la (2) e la (3), si ha (ricordando che ac = dy/dt):

dt_O = dy/ac + (Y – dy)/(c sen(ϑ)) - Y/(c sen(ϑ))

dt_O = (dy sen (ϑ) + a(Y – dy) – Ya)/(ac sen(ϑ))

dt_O = (dy sen (ϑ) – a dy)/(ac sen(ϑ))

dt_O =  dy(sen (ϑ) – a )/(ac sen(ϑ)) = (dy/c) (sen (ϑ) – a)/(a sen(ϑ))

Non ci resta che calcolare la velocità dell’ombra, che è data semplicemente dal rapporto tra lo spazio (dx) e il tempo (dt_O), ricordando la (1):

v_O = dx/dt_O = dy cot(ϑ)/((dy/c) (sen (ϑ) – a)/(a sen(ϑ)))

v_O = c (cos(ϑ)/sen(ϑ))(a sen(ϑ))/(sen (ϑ) – a)

v_O = a c cos(ϑ)/(sen(ϑ) – a)          …. (4)

Questa è la funzione che possiamo descrivere nella Fig. 13, per un certo valore di ϑ (ad esempio, come prima, lo scegliamo uguale a 30°). L’unica variabile è ovviamente a che al suo variare ci fornisce i vari valori di v_O.

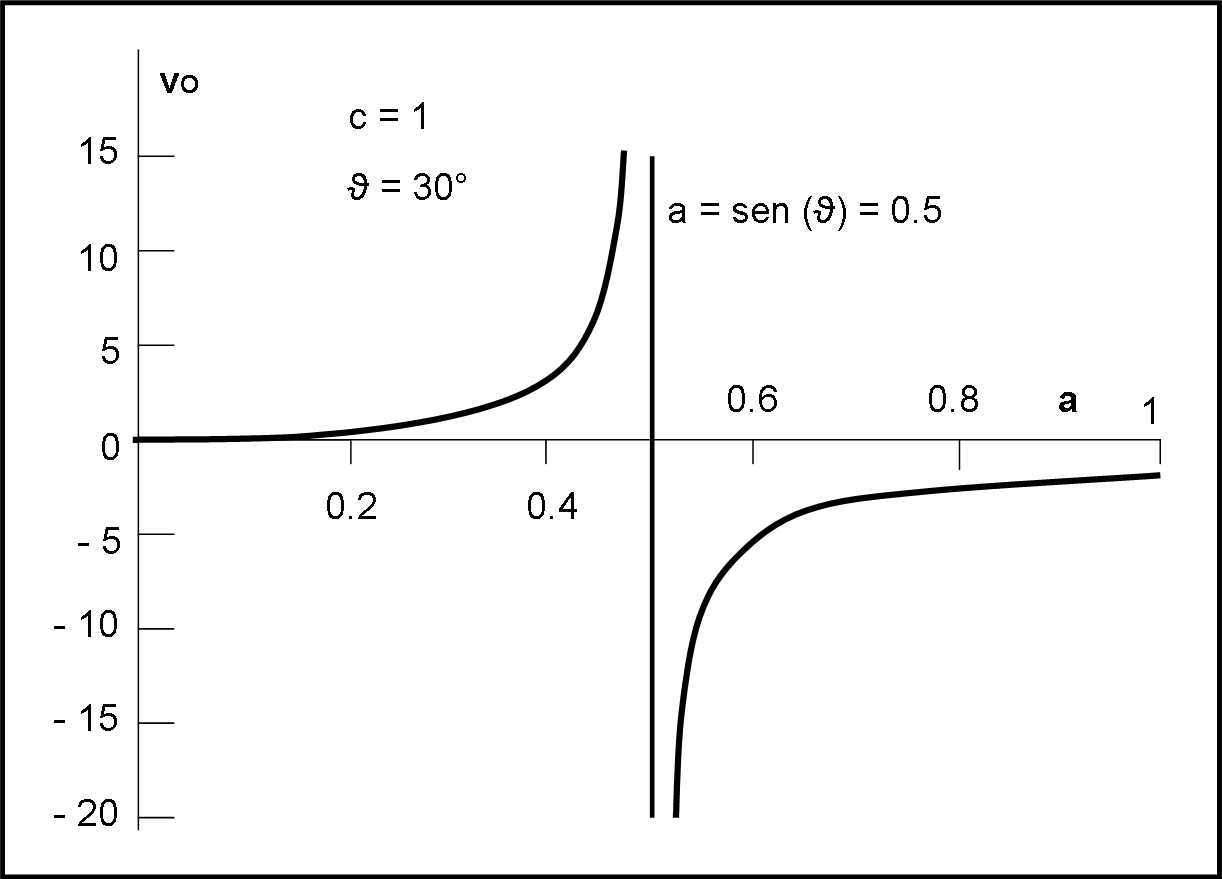
Notiamo subito che il denominatore va a ZERO, ossia la funzione va a infinito, proprio per a = sen(ϑ), la situazione limite per l’inversione del verso dell’ombra, come avevamo trovato nella trattazione precedente: la matematica non può che confermare i risultati ottenuti con un “giusto” ragionamento e non fa altro che rendere sintetica e immediata l’intera visualizzazione.

Analogamente si spiega molto bene perché la velocità è positiva, per a < sen(ϑ), e negativa, per a > sen(ϑ).

Non è nemmeno difficile comprendere che per a = 1 (scorrimento dello schermo pari alla velocità della luce… che Einstein ci perdoni!), il valore della velocità resta un valore finito e diverso da zero.

Notiamo, infine, che se a e molto piccolo, ossia se a << sin (ϑ), la (4) ci regala la ben nota relazione:

v_O = ac cot(ϑ)

che avevamo usato precedentemente, quando si poteva considerare istantaneo il viaggio della luce.

Divertitevi pure a cambiare l’angolo ϑ, come fatto da Paolo, e a calcolare quanto poco ci vuole per viaggiare a velocità pazzesche, a cavallo di un’ombra come spiega questo racconto. A riguardo inseriamo, con molto piacere, la splendida e simpaticissima vignetta eseguita da Paolo, relativa al racconto che lo vede … protagonista.

Non alzate quello schermo

Come promesso, dimostriamo che NON si possono raggiungere velocità superiori a quelle della luce alzando lo schermo, invece che abbassandolo.

Il primo raggio parte dal basso e deve percorrere il tragitto minore (ossia B’C’). Il suo ritardo per arrivare in C’ è dato, ovviamente, da dt₂. Poi, lo schermo scorre verso l’alto in un tempo dt. L’ultimo raggio arriva in C con un ritardo uguale a dt₁.

L’intervallo di tempo che ci serve per calcolare la velocità dell’ombra (sempre da C’ verso C) è dato questa volta da:

dt_O = dt + dt₁ - dt₂ = dy/ac + Y/(c sen(ϑ)) - (Y - dy)/(c sen(ϑ))

Calcolando v_O = dx/dt, come fatto precedentemente, si ottiene:

v_O = ac cos (ϑ)/((sen(ϑ) + a)     …. (5)

che è completamente diversa dalla (4). Se a fosse anche uguale a 1, ma ϑ ≠ 0, il denominatore sarebbe maggiore di 1. Il numeratore sarebbe uguale a qualcosa di più piccolo di c e quindi il risultato sarebbe una velocità minore di c.

In Fig. 14 riportiamo il grafico relativo per ϑ = 30°.

Un articolo lungo, ma non troppo complesso (se seguito con attenzione). Grazie, soprattutto, ai nostri più accaniti e preparati lettori NON silenziosi, l’ombra e la sua velocità non hanno più segreti. E anche Einstein non ha dovuto saltare sulla sedia!

QUI potete continuare a divertirvi aiutando il nervoso Ulisse a fuggire dalla sua ombra!

Mentre QUI potete scoprire qual è la parte più... "luminosa" dell'ombra e, soprattutto, perché!