Quiz astronomico sul Sole usato come telescopio. 2 ***

09/06/18

Quiz astronomico sul Sole usato come telescopio. 2 ***

Categorie: Matematica Quiz Relatività Tags: Scritto da: Vincenzo Zappalà Commenti:9

La soluzione del quiz della volta scorsa la darò insieme a quella di questa seconda parte (anche se nei commenti è facile dedurre il procedimento approssimato da svolgere). Proseguiamo nello "studio" pratico dell'effetto lente del grande Albert.

In poche parole, abbiamo visto che il Sole riesce a far convergere la luce di una stella lontanissima in un punto non così lontano (il nostro Sedna potrebbe passare benissimo per quel punto…). Ciò ci fa capire che attraverso il Sole riusciamo a vedere qualcosa che dovrebbe nascondersi dietro di lui a grande distanza. Ma l’effetto lente, previsto dalla relatività generale, e continuamente confermato e utilizzato, deve fare molto di più. Infatti, il nome stesso lo dice… se si chiama LENTE , lente deve essere, ossia deve riuscire a immagazzinare più luce rispetto a una visione diretta, proprio come fanno i telescopi.

Attenzione: non parliamo di ingrandimenti (l’incubo degli astrofili di basso rango), ma di quantità di luce, ossia di quantità d’informazione, il vero scopo dei telescopi.

Immaginiamo allora che Ist sia l’intensità luminosa della stella posta all’infinito e cerchiamo di calcolare, in modo estremamente semplice e approssimato, di quanto il Sole riesca ad amplificare la luminosità raccolta su un certo ricevitore.

Poniamo, ad esempio, un dischetto “sensibile” nel punto di fuoco minimo della volta scorsa e chiediamoci quale sarà il flusso luminoso ricevuto da questo cerchietto. Anzi, facciamo ancora di più: calcoliamo il rapporto tra il flusso ricevuto, senza il Sole, e quello ricevuto, con il Sole, sulla stesso dischetto ricettore. Ridendo e scherzando e con pochi passaggi, troveremo un fattore importantissimo per lo studio dell’Universo lontano: il fattore di amplificazione dell’effetto lente. E dico poco…

Ovviamente viene esclusa la luce proveniente dal Sole..

Un quiz altamente istruttivo e decisamente semplice, se approssimato con intelligenza e intuito.

Non si richiedono conti numerici, ma solo una formuletta finale di estrema semplicità, funzione di due soli parametri, ben conosciuti, che risultano fondamentali. La parte più difficile è proprio il saper semplificare i calcoli, eliminando, in modo corretto, i termini decisamente trascurabili. Nessuno pretende la formula completa… anzi, la parte più interessante è proprio saper trafficare con cosa poter buttare via e cosa dover tenere ben stretto.

Forza… il quiz è aperto a tutti e non ha difficoltà matematiche di rilievo…

 

QUI la soluzione (e un approfondimento sull'effetto lente)

Articoli correlati

9 commenti

  1. Vincenzo Zappalà
    10/06/2018 at 07:44

    Beh?! I "maghi" sono solo matematici e geometrici? e quelli astronomici? guardate che per risolverlo ci vuole solo un po' di geometria e matematica: sono o non sono il linguaggio della fisica???? :roll:  :?:

  2. Vincenzo Zappalà
    11/06/2018 at 16:17

    va beh... un piccolo aiuto...

    Il concetto è lo stesso dell'altra volta in cui si è trovato un punto. Ma cosa succede se allontaniamo i raggi rispetto al Sole? Cambia il fuoco oppure no? E se mettiamo un dischetto nel primo fuoco, gli altri raggi lo colpiscono oppure no? Non possiamo certo allontanarci troppo dal Sole se no il dischetto non viene toccato... Inoltre, a noi interessa poco la messa a fuoco... per quello ci penserà qualcos'altro. La luce che colpisce uno specchio aumenta con l'aumentare dello specchio.... ma sullo specchio non è certo a fuoco...

  3. Vincenzo Zappalà
    11/06/2018 at 16:19

    Aggiungo ancora... Sicuramente il mio dischetto deve avere dimensioni "umane" e quindi di diametro piccolo... per cui è facile trovare quel qualcosa che ci permette di eliminare molti termini e ottenere una formula quasi banale...

    non deludetemi.... in fondo è un problema di ... matematica applicata!

  4. Fabrizio
    11/06/2018 at 18:31

    Ci provo.

    I fotoni tangenti al sole arrivano sul centro del dischetto, perché è proprio li che abbiamo messo il dischetto.

    Quindi sul dischetto penso che  arrivino i fotoni provenienti dall'infinio che attraversano una corona circolare intorno al sole.

    Se il dischetto è piccolo anche la larghezza della corona circolare dovrebbe essere piccola. Questo mi dovrebbe permettere di assumere che la deviazione dei fotoni rimane circa la stessa. Da questo posso dedurre che la larghezza della corona circolare è uguale al raggio del dischetto.

    L'amplificazione richiesta è il rapporto tra le aree della corona circolare e del dischetto.

    Se r è il raggio del sole e s è il raggio del dischetto avrei:

    A=\frac{\pi\:(r+s)^2-\pi\:r^2}{\pi\:s^2}=\frac{\pi\:(2\:r\:s+s^2)}{\pi\:s^2}\approx2\:\frac{r}{s}

     

     

  5. Vincenzo Zappalà
    11/06/2018 at 18:37

    la strada è buona, ma la deviazione dei fotoni non può essere la stessa (basta poco per cambiare di molto il fuoco). Questa non è un'approssimazione perfetta, ma potrebbe anche essere accettata... prova a tener conto di un fuoco differente... la cosa cambia di poco... Un bravo, comunque, a Fabry... non si smentisce mai!!!!

  6. Fabrizio
    12/06/2018 at 01:43

    Cerco di considerare la differente deviazione dei fotoni che passano a diversa distanza dal sole.

    r: raggio del sole, s:raggio del dischetto, R: raggio esterno della corona circolare dalla quale provengono i fotoni che arrivano sul dischetto

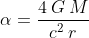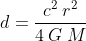    Se non ho capito male la formula della deviazione, i fotoni che arrivano al centro del dischetto sono deviati di un angolo \alpha =\frac{4\:G\:M}{c^2\:r}. Da questa formula si deriva cha la distanza del fuoco minimo è d=\frac{c^2\:r^2}{4\:G\:M}.

    La deviazione β dei fotoni che arrivano sul bordo del dischetto dovrà essere tale che

    \beta\:d=R-s

    \frac{4\:G\:M}{c^2\:R} \frac{c^2\:r^2}{4\:G\:M}=R-s

    \frac{r^2}{R}=R-s

    R^2-s\:R-r^2=0

    che ha come soluzione che ci interessa

    R=\frac{s}{2}+\frac{\sqrt{s^2+4\:r^2}}{2}\approx r+\frac{s}{2}

    L'amplificazione è il rapporto tra le aree della corona circolare e del dischetto.

    A\approx \frac{\pi\:(r+s/2)^2-\pi\:r^2}{\pi\:s^2}=\frac{r\:s+s^2/4}{s^2}\approx \frac{r}{s}

     

  7. Vincenzo Zappalà
    12/06/2018 at 06:28

    vedi Fabry... in fondo c'era solo un fattore 2...Una bella amplificazione.... non trovi? :wink:

  8. Fabrizio
    12/06/2018 at 13:31

    Certo, una concentrazione elevatissima.

    Ma ciò che mi ha lasciato in dubbio sulla correttezza della mia risposta è stato il fatto che questo fattore di amplificazione non dipendesse da M. M agisce solo su d e non su questo fattore.

    Un altra cosa "strana" è che se allontaniamo il nostro sensore il fattore di amplificazione aumenta, almeno idealmente.

  9. Vincenzo Zappalà
    12/06/2018 at 14:15

    caro Fabry,

    la massa interviene nella deviazione dei raggi... anche se poi sparisce. E più è grande e maggiore è l'anello che converge. Ovviamente, viene considerata la sorgente all'infinito e l'intensità costante a qualsiasi distanza. Se mettessimo una sorgente puntiforme e i raggi che partono da lei , arriverebbe sempre meno luce sul rivelatore.

    A parità di condizioni, questo è però il fattore di amplificazione (estremamente semplificato).

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.