Il presente articolo è stato inserito nella pagina di approfondimento dedicata all'effetto lente gravitazionale

 

Questo articolo rappresenta praticamente la soluzione ai due quiz (QUI e QUI) sulla deviazione della luce per effetto di una grande massa (e ne contiene uno ulteriore), ma è meglio che viva indipendentemente come ulteriore analisi (approssimata) della celebre e utilissima lente gravitazionale di Einstein. Faremo conoscenza con un fantastico telescopio "naturale" non molto lontano da noi. Chissà...

Ricordiamo brevemente che già la teoria di Newton prevedeva (vedi QUI) una deflessione della luce, dipendente dalla massa del corpo centrale, dato che l’accelerazione di gravità è indipendente dalla massa del corpo che la subisce (come aveva intuito Galileo). Ne consegue che poco imposta che la massa del fotone sia piccola o nulla. Il risultato, in un primo momento, era del tutto simile a quello proposto dalla RG di Einstein. Solo in un secondo tempo il grande Alberto trovò l’errore e concluse con un effetto “doppio” rispetto a quello di Soldner.

Possiamo, perciò, scrivere senza esitazione la formuletta più o meno approssimata che definisce l’angolo di deflessione della luce quando passa vicino a una massa considerevole. La migliore definizione si riferisce non tanto alla massa in sé, ma al raggio di Schwarzschild, che stabilisce chiaramente quanto sia concentrata la massa.

Abbiamo già studiato come la luce si comporti vicino a un oggetto la cui massa sia completamente interna al raggio di Schwarzschild (QUI), ma è altrettanto interessante analizzare ciò che capita vicino a una stella “normale” come il Sole. Anche se la sua capacità di deflettere è decisamente ridotta, ciò non toglie che rimanga un ottimo esempio per studiare l’effetto lente in modo estremamente semplice ed efficace.

La formula (la sua deduzione attraverso la RG non è cosa banale…) è la seguente:

ϑ = 2R_Sc/r            …. (1)

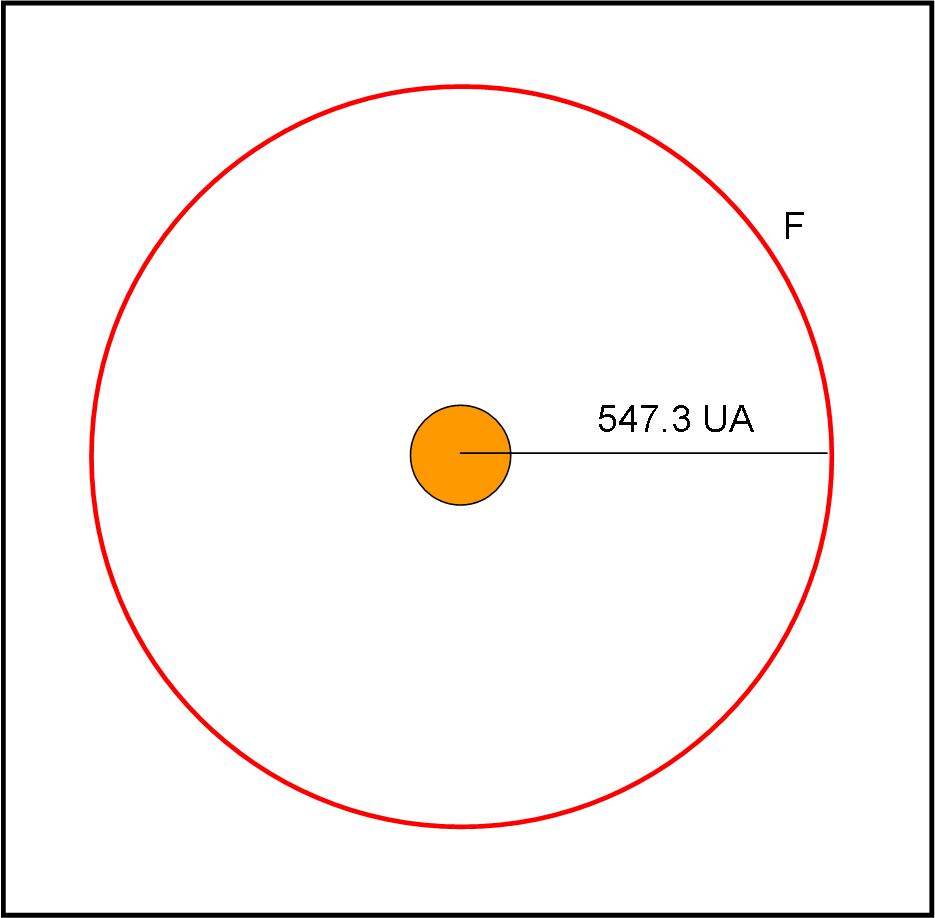
Dove ϑ è l’angolo di deflessione, R_Sc è il raggio di Schwarzschild (funzione della massa) e r il parametro d’impatto, ossia la distanza tra l’asse centro del Sole-fuoco finale dei raggi luminosi e il raggio proveniente dalla stella (considerata all’infinito). Tutto è decisamente più chiaro guardando la Fig. 1.

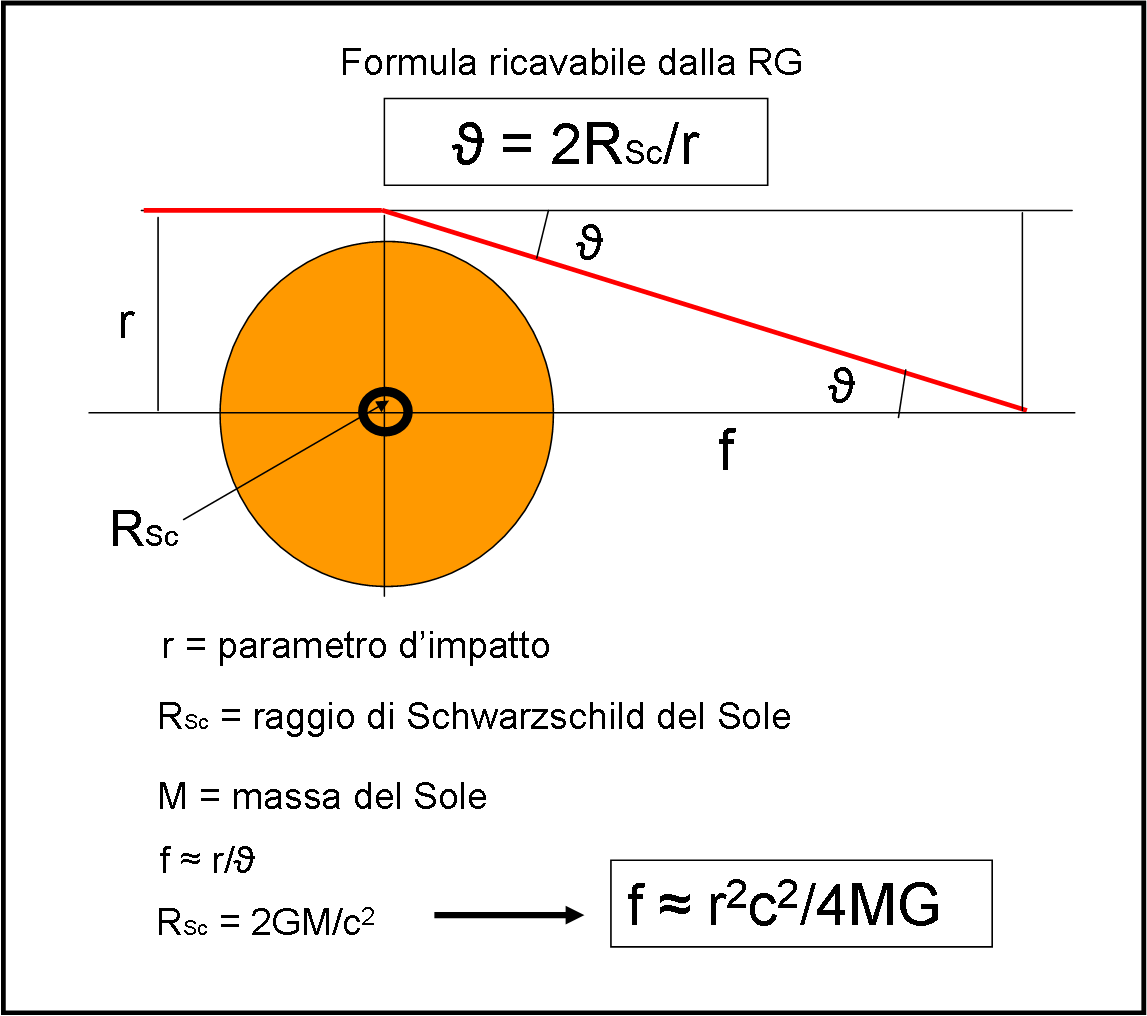
Notate che abbiamo usato una semplificazione (non così tragica): il raggio si piega nel punto di minima distanza dal Sole, mentre, in realtà, dovrebbe piegarsi gradatamente…

Abbiamo definito come distanza focale f, la distanza tra il centro del Sole e il fuoco in cui convergono i raggi, come quello rappresentato in figura a distzanza r dal centro del Sole.

Una banale geometria ci permette di scrivere che l’angolo ϑ è legato a r e alla distanza f attraverso la relazione

tan ϑ = r/f

Data la piccolezza degli angoli in gioco è ammissibile scrivere:

ϑ ≈ r/f

L’angolo è noto dalla (1) e  possiamo scrivere:

2R_Sc/r ≈ r/f                   …. (2)

Ma sappiamo molto bene che:

R_Sc = 2GM/c²

Sostituendo nella (2) si ha:

f = r²c²/4MG                  ….(3)

La (3) ci permette di calcolare per ogni distanza r (parametro d’impatto) il fuoco dei raggi provenienti dalla stella supposta all’infinito (raggi paralleli).

Dove cadrà il fuoco “minimo” (f₁) ossia quello più vicino al Sole? Beh… il primo raggio luce utile per costruire questo strano e ingombrante telescopio è il raggio che “sfiora” il Sole , ossia r = R, come rappresentato in Fig. 2.

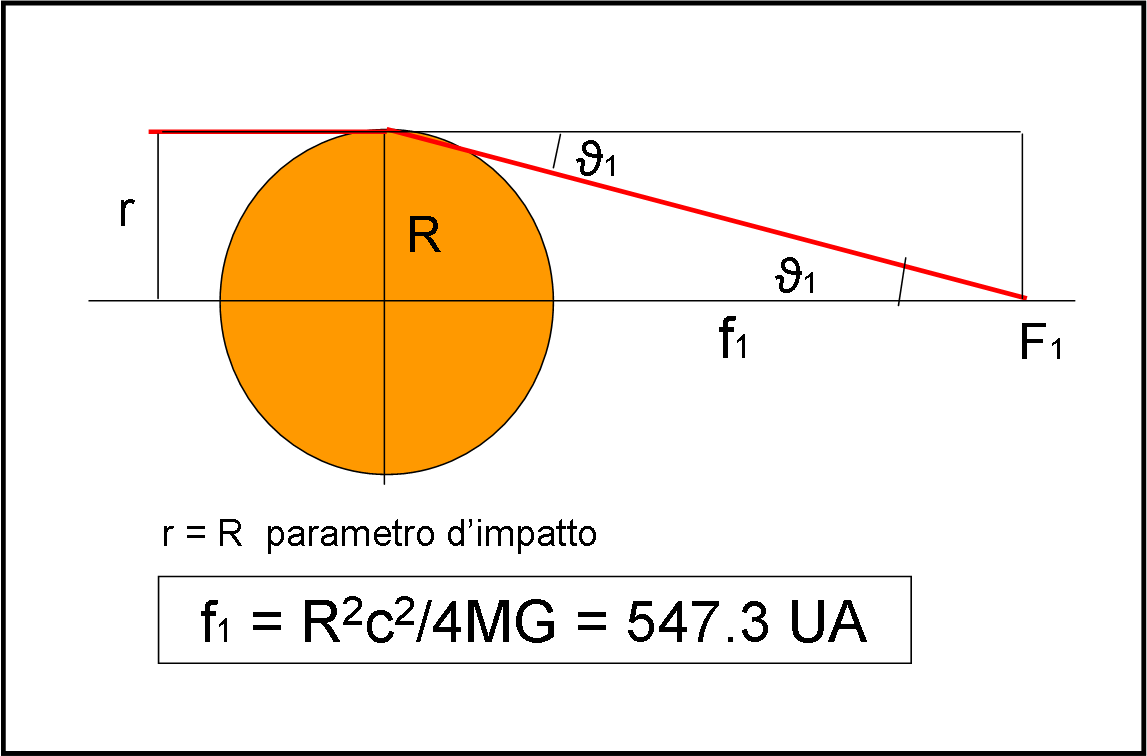
La  (3) diventa:

f₁ = R²c²/4MG

I parametri al secondo membro sono tutti noti e il risultato è il seguente:

f₁ = 547.3 UA

Una lunghezza enorme rispetto al raggio, non certo piccolo, del Sole. Tuttavia, un abitante di Sedna o di altri oggetti transnettuniani a grande eccentricità potrebbero anche recarsi in quel punto così importante. Chissà che folla di astrofili sedniani…

Tuttavia, un telescopio che si rispetti deve raccogliere più luce possibile e quindi vogliamo inserire un dischetto capace di ricevere la luce della stella proprio nel punto F₁. Più è grande è meglio è, ma non possiamo certo costruire rilevatori di dimensioni planetarie (anche se non conosciamo le dimensioni dei sedniani…).

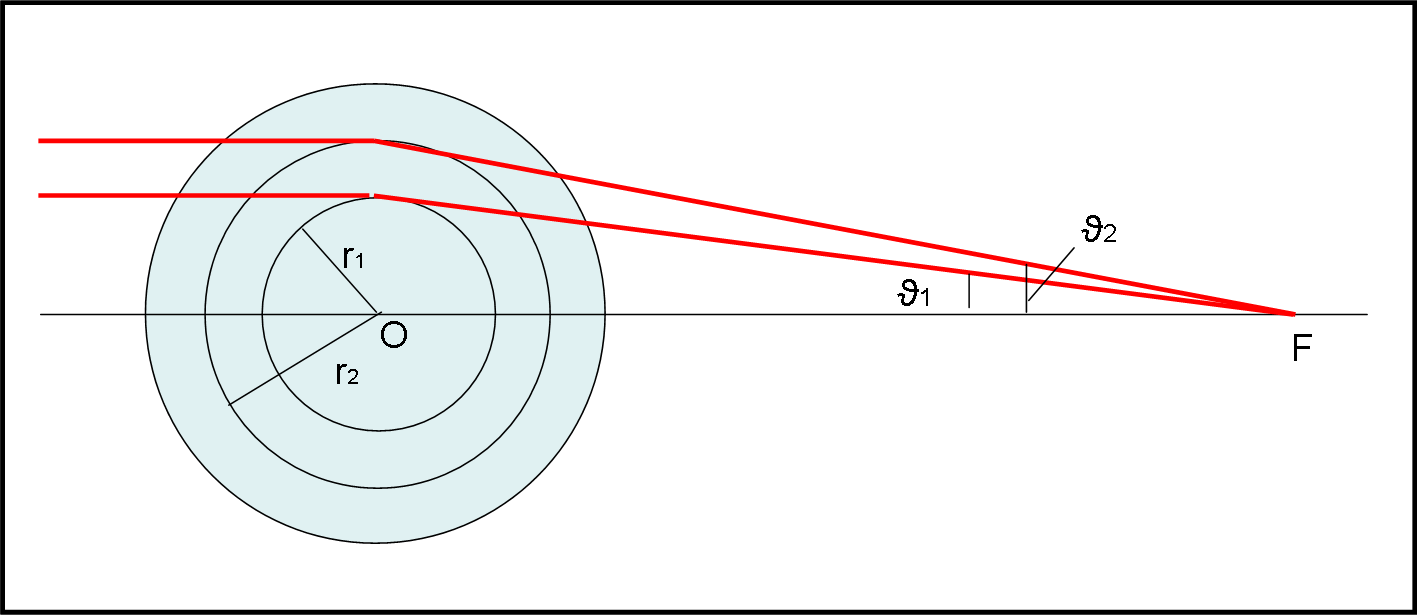
Inseriamo, perciò, in F₁ un dischetto di raggio d, capace di raccogliere anche raggi della stella non proprio radenti al Sole.

Il raggio limite che riesce a toccare il bordo di d passerà a una distanza h dal bordo del Sole prima di essere deviato. Essendo un po’ più distante dobbiamo tener conto che il suo angolo di deflessione ϑ₂ sarà u po’ più piccolo di ϑ1 e la sua distanza focale un po' più lunga (ricordiamoci che basta una piccolissima differenza nell’angolo per avere una variazione non trascurabile).

La Fig. 3 ci illustra la situazione.

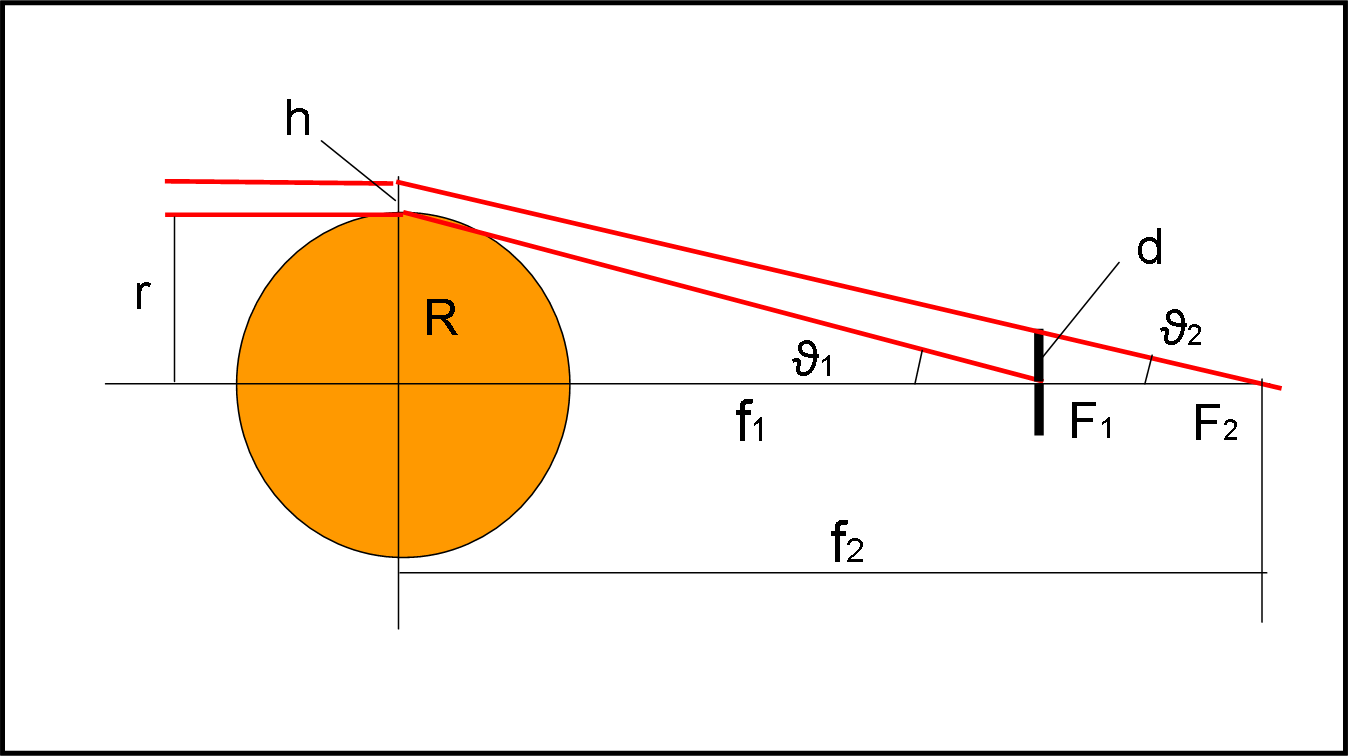
E’ immediaato scrivere quanto vale f₂, ricordando la (3) in cui possiamo tranquillamente lasciare il raggio di Schwarzschild

f₂ = (R + h)²/2R_Sc

Lavorando sempre con angoli molto piccoli possiamo scrivere senza problemi:

(f₂ - f₁)/d ≈ ϑ₂

ossia (utilizzando anche la (1)):

d = (f₂ - f₁)/ϑ2 = ((R + h)²/2R_Sc - R²/2R_Sc) (2R_Sc/(R +h))

semplificando:

d =  ((R + h)² – R²)/(R + h) = (R² + h² + 2hR – R²)/(R + h)

d = (h² + 2hR)/(R + h)

A questo punto ragioniamo un po’ sulle grandezze in gioco. Sicuramente abbiamo che h << R. Il che vuol dire che si possono tranquillamente eliminare le potenze di h e fermarci al primo grado. Ossia possiamo porre h² = 0

d ≈ 2Rh/(R + h)

Dividiamo numeratore e denominatore per R (sicuramente non è uguale a zero):

d ≈ 2h/(R/R + h/R)

d ≈ 2h/(1 + h/R)

ma h/R è sicuramente una quantità che può essere trascurata.

Si ha, infine:

d ≈ 2h           …. (4)

 Ora possiamo occuparci della luce che proviene dalla stella. Essa ha un’intensità I_st. Definiamo come amplificazione A, dovuta all’effetto lente, il rapporto tra il flusso ricevuto sul dischetto di raggio d nel caso che sia presente il Sole e nel caso che esso venga annullato (Fig. 4).

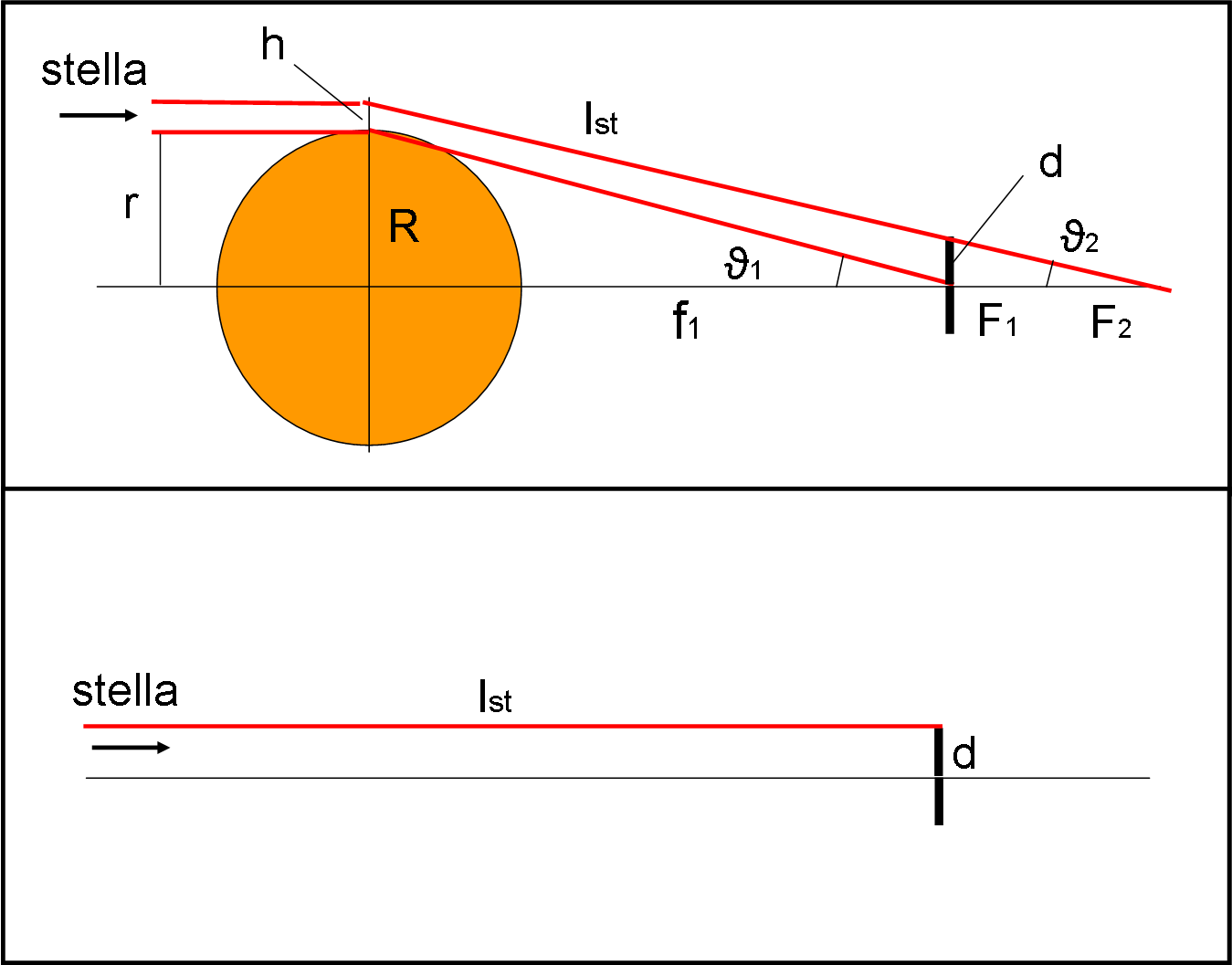
Nel secondo caso la luce che giunge sul dischetto è proprio quella contenuta in un cilindretto di raggio d. Nel primo caso è quella che proviene dalla corona circolare compresa tra il Sole e una sfera di raggio R + h. Noi possiamo, comunque, lavorare sempre nel piano della figura.

Il flusso ricevuto è  dato dal prodotto tra l’intensità luminosa (costante) e la superficie da cui proviene la luce, ossia:

A = I_st · area corona circolare di raggio (R + h)/I_st · cerchio di raggio d

A = (π(R+ h)² – πR²)/(πd²)

A = (R²+ h²+ 2Rh – R²)/d²

Semplificando e trascurando il termine in h², si ottiene:

A ≈ 2Rh/d²

Ricordando la (4), si ha infine:

A ≈ 2Rd/2d²

A ≈ R/d

Per un raggio di un metro avremmo un’amplificazione pari a più di 6 ·10⁸. Niente male… direi, pur tenendo conto che le magnitudini vanno con il logaritmo…

Notiamo che non esiste certo un solo fuoco minimo, ma essi descrivono una sfera con centro nel Sole. Infatti le stelle hanno direzioni qualsiasi e non per niente si distribuiscono su una sfera… celeste. In Fig. 5

Dato che la Nube di Oort è ancora più lontana, non sarebbe impossibile inserire un ricevitore in orbita attorno al Sole e magari fargli anche cambiare piano orbitale. Mamma mia, che spettacolo sarebbe!

Inoltre, la deflessione è anche funzione della lunghezza d’onda e così lo è anche il fuoco. Basterebbe spostarsi lungo l’asse … ottico e avere una specie di fantastico spettrografo!

In realtà, una missione in grado di raggiungere quel luogo è già stata proposta… Per non farsi prendere dall’euforia, ricordiamo, però, che la corona solare non è certo un limite trattabile facilmente e che 500 Unità Astronomiche non sono una bazzeccola.

Facciamo ancora un passo in avanti, anche se la faccenda diventa più un esperimento mentale che una realtà fisica… Cerchiamo di trattare la lente stellare come una vera lente. Finora, infatti, abbiamo considerato la luce che proviene dall’esterno della lente, dato che il Sole non si fa certo attraversare dai fotoni della stella lontana. Creiamo un modello particolare, che, solitamente, è descritto come materia oscura. Essa sarebbe l’ideale, dato che la luce  può attraversarla impunemente, subendone, però, tutti gli effetti gravitazionali.

Noi, invece, prendiamo qualcosa di meno “astratto”, ma che può darci comunque un’idea del problema. Ad esempio, un ammasso globulare o anche un ammasso galattico (che però ha un po’ troppo gas e polvere nel suo centro). Immaginiamoci, quindi, una struttura di grande massa che possa comunque essere attraversata dai raggi luminosi di una stella lontana senza bloccare troppo la luce che la investe. Assumiamo che le stelle seppur tantissime diano poco fastidio ai raggi provenienti dall’infinito.

Possiamo perciò considerarla come una vera lente che si lasci attraversare dai raggi luminosi (e se poi sono tutti affievoliti, ammettiamo che lo siano in modo continuo).

Il problema che ci poniamo è il seguente: quale deve essere la distribuzione della massa al variare del raggio affinché tutti i raggi si concentrino in un solo fuoco. Una vera lente convessa, in poche parole…

Chi vuole provare a risolverlo da solo non avrà molte difficoltà, e interrompa la lettura. Noi, intanto andiamo avanti…

Costruiamo la Fig. 6 dove al posto del Sole inseriamo una massa “penetrabile” dai raggi luminosi di una stella lontana e imponiamo che tutti questi raggi si concentrino in un solo fuoco. Dobbiamo fare un’ulteriore semplificazione: la massa che è causa della deflessione dei raggi sia solo quella interna al raggio considerato.

Indichiamo con M(r) la massa interna al raggio che ha come parametro d’impatto r. Ovviamente, più il raggio si avvicina al centro della “lente” è minore è la sua deflessione (la massa che lo costringe a deviare diminuisce e, quindi, anche il relativo raggio di Schwarzschild).

Indichiamo due raggi qualsiasi a distanza r₁ e r₂ dal centro della massa-lente. I raggi vengono deflessi secondo le solite regole, tenendo in conto la massa che racchiudono. Abbiamo:

f_i = r_i²/2RSc_i = r_i²c²/4GM_i              (i = 1,2)

Basta imporre che f₁ = f₂ e si ottiene:

r₁²/r₂² = M₁/M₂

Il che vuol dire che la massa deve variare in funzione del raggio al quadrato

M(r) ∝ r²

Una bella sfida… ma che telescopio!!!