Il presente articolo è stato inserito nella pagina di approfondimento dedicata all'effetto lente gravitazionale

 

Attraverso semplici approssimazioni, più che valide per le distanze in gioco, è facile ricavare la rappresentazione geometrica della lente gravitazionale che può immediatamente legarsi a quanto previsto da Einstein. Un esercizio molto più semplice di quanto ci si aspetti.

Il nome lente gravitazionale è estremamente indicativo e anche giustificato, sempre che si capisca bene il funzionamento di una lente comune e di una relativistica. Diamone una spiegazione molto succinta, ma sufficiente e intuitiva.

Una lente comune è costruita in modo che più i raggi luminosi si allontanano dal centro e più vengono deviati. Solo in questo modo si può aggiungere luce a luce sull’immagine che si forma nel fuoco. Per una trattazione diversa, ma estremamente istruttiva, si può anche andare QUI, dove la lente entra a far parte della QED (QUI, invece, troverete una spiegazione delle lenti più comuni usate per i telescopi).

Nella lente gravitazionale capita il contrario. Più il raggio di luce passa lontano dalla lente vera e propria e sempre meno viene deviata. Ovviamente, le differenze non si fermano qui, ma il risultato finale è estremamente simile: una concentrazione di luce in punti particolari (uno solo per la lente normale, più punti per la lente gravitazionale).

In modo non banale si può anche dimostrare che la lente gravitazionale non solo fa vedere cose che non si potrebbero vedere perché nascoste, ma ingigantisce anche la loro luminosità. Abbiamo uno strumento ottico, basato sulla relatività generale, che sembra costruito proprio per permetterci di conoscere l’Universo più lontano. Einstein lo ha previsto in modo mirabile, ma resta il fatto che la Natura ce l’ha offerto su un piatto d’argento…

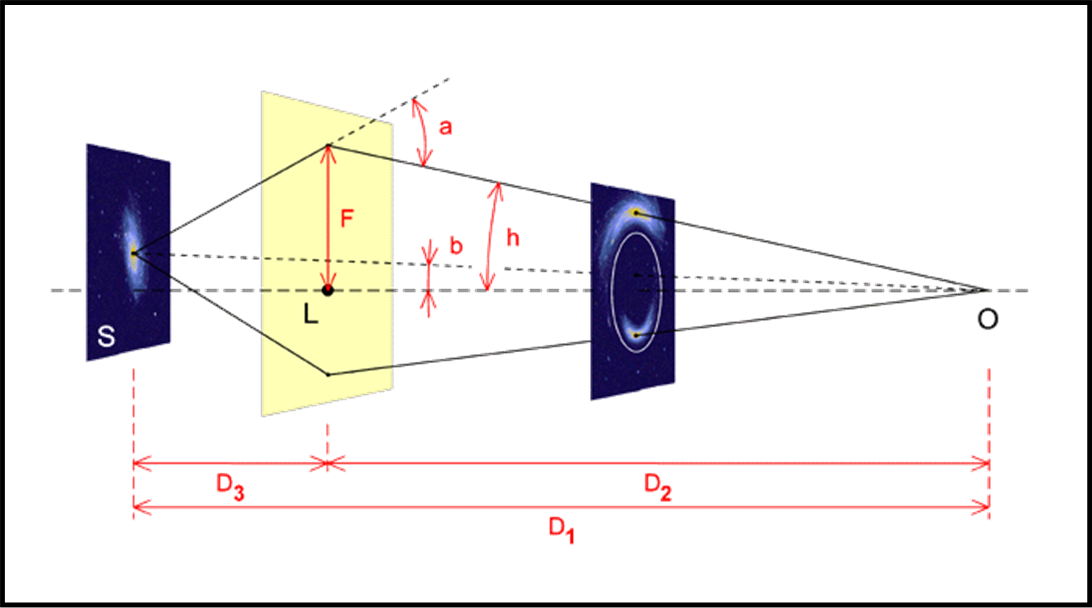
Bene, dirigiamoci verso il nocciolo del problema. Rappresentiamo nella Fig. 1 la situazione trasportata su un piano che contenga la sorgente lontana S, la lente gravitazionale L e l’osservatore T. Inoltre, consideriamo sorgente e lente come oggetti “puntiformi”.

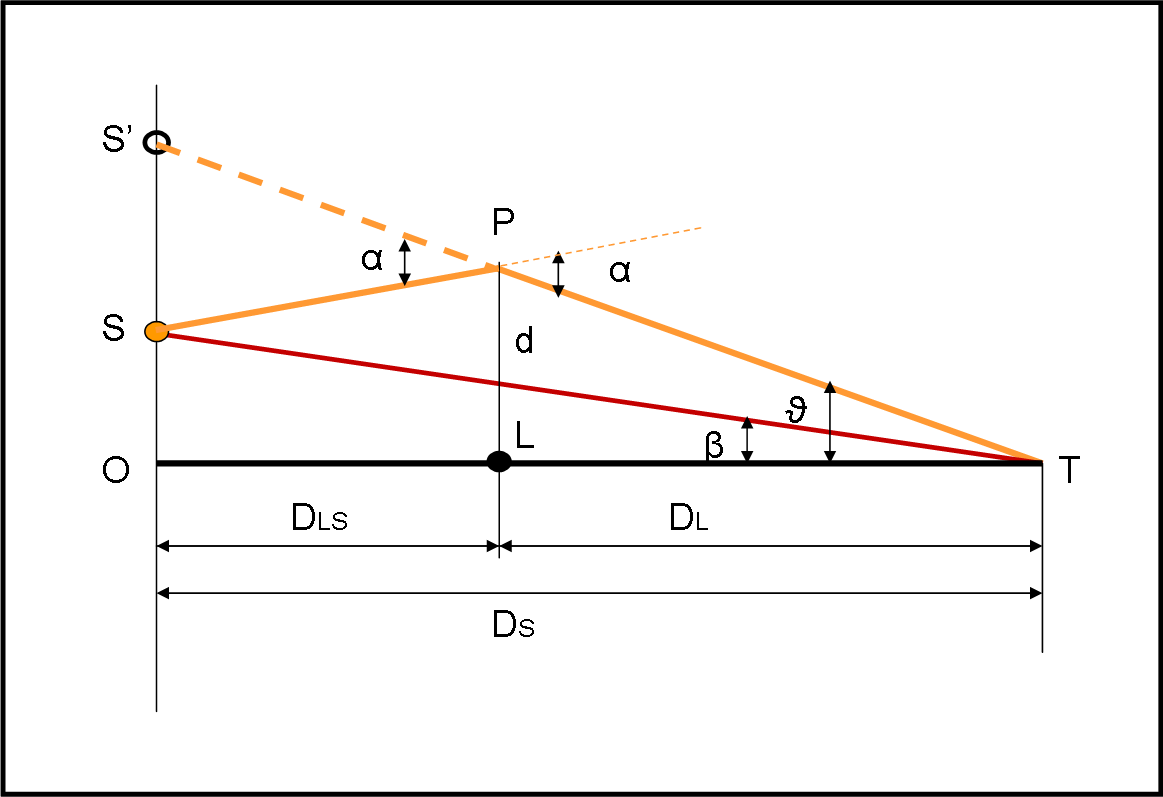
La sorgente invia i suoi fotoni verso il Cosmo. Noi siamo interessati al fotone che passa per P a una certa minima distanza d dalla lente gravitazionale. Permettiamoci di rappresentarlo come un raggio di luce. In realtà, il raggio comincia a deviare prima di raggiungere P e continua anche dopo. Per semplicità, noi lo facciamo piegare di un angolo α proprio in P (le cose cambiano di poco).

Il raggio, così deviato, giunge all’osservatore T, formando un angolo ϑ con la direzione della lente L. Possiamo anche tracciare la congiungente ST che, in generale, è nascosta da L, ma che nel caso di oggetti puntiformi potrebbe anche essere in vista. Diciamo “potrebbe”, perché, in realtà, questo raggio diretto sarebbe deviato molto più di quello passante per P (a differenza di ciò che capita nella lente comune), non arrivando mai all’osservatore T. Chiamiamo β l’angolo all’osservatore T, tra S e L.

A questo punto, cominciamo con le approssimazioni … Non pensiamo, però, di fare cose esagerate. Ricordiamo, infatti, che le distanze tra noi e la sorgente e la lente (e tra loro due) sono enormemente più grandi che le distanze sottese nella loro posizione dagli angoli sopra descritti (anche milioni di volte). In altre parole, la separazione angolare è veramente piccola.

Innanzitutto, ricordiamo una cosa ben nota a tutti: in un triangolo isoscele che abbia i due lati uguali enormemente più lunghi del terzo lato, si può assumere che l’angolo tra i lati uguali, espresso in radianti, moltiplicato per il lato lungo, sia uguale al lato corto. In realtà, quello che si fa è considerare un cerchio che ha per raggio il lato lungo e uguagliare l’arco di cerchio, corrispondente a un piccolo angolo, alla corda che congiunge i suoi estremi, come mostrato in fig. 2.

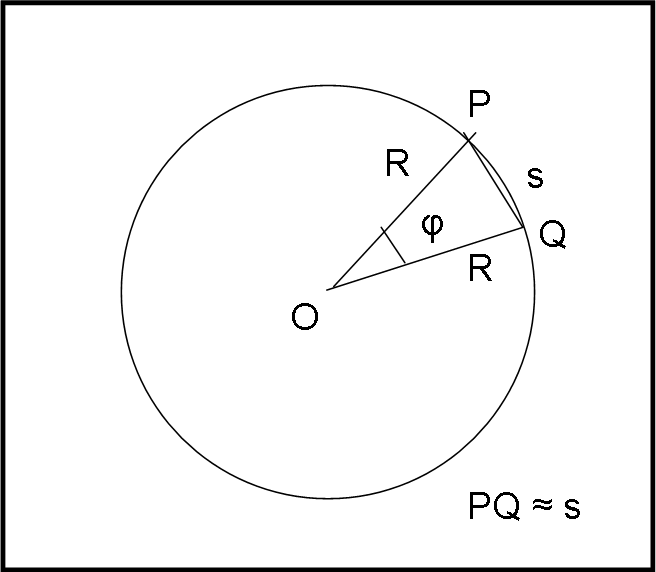
Infatti, come spiegato nelle lezioni di geometria sferica, vale la relazione ben conosciuta:

2πR : s = 360 : φ

Ossia

s = R φ

Ma s può essere assunto uguale a PQ e quindi:

PQ ≈ R φ

Proprio quello che volevamo…

Inoltre (seconda approssimazione), se consideriamo distanze misurate su un piano passante per la sorgente, possiamo considerare isoscele ogni triangolo che ha per lato corto una piccola distanza misurata su questo piano e per vertice un punto sul piano della lente. La fig. 3 ci aiuta a capire meglio cosa intendiamo dire: il triangolo può essere considerato isoscele e quindi vale ciò che abbiamo appena detto.

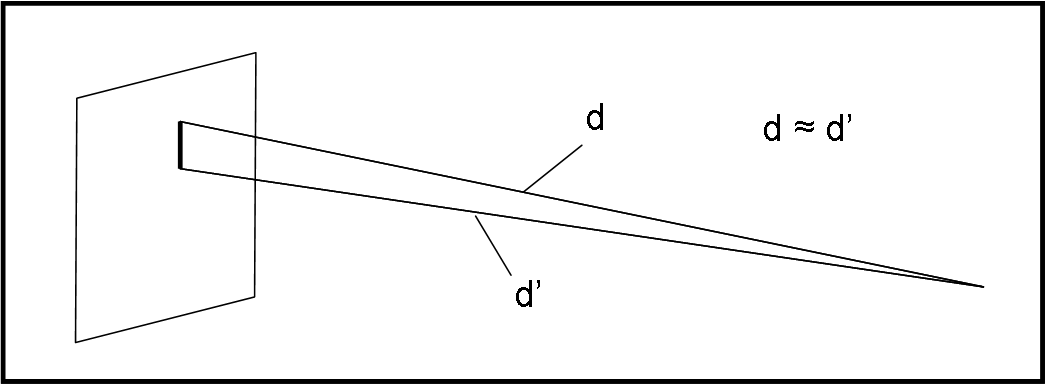
Tornando alla Fig. 1, si ha:

S’S ≈ α PS ≈ α D_LS

Ovviamente, date le distanze relative non vi sono problemi a sostituire PS con LO (= D_LS). Non spaventatevi guardando la figura… tutti gli angoli sono stati enormemente ingranditi così come sono state rimpicciolite le distanze. Il tutto si svolge vicinissimo a L.

Senza pensare a triangoli isosceli, l’approssimazione si ripete per i triangoli TS’O e TSO. In questi due casi possiamo scrivere:

tan ϑ = S’O/D_S

e

tan β = SO/D_S

Ed è facile approssimare a:

ϑ ≈ S’O/D_S

β ≈ SO/D_S

da cui:

S’O ≈ ϑ D_S

SO ≈ β D_S

Possiamo scrivere, guardando la Fig. 1:

S’O = S’S + SO

Ossia:

ϑ D_S = α D_LS + β D_S

e, infine:

α = (D_S/ D_LS) ϑ + (D_S/ D_LS) β       …. (1)

Anche se sembra di aver giocato in modo elementare con qualche triangolo, ciò che abbiamo ricavato si chiama equazione della lente ed è di interesse fondamentale per il calcolo dei vari parametri in gioco. In realtà, si dovrebbe considerare la lente come un oggetto esteso, di forma più o meno allungata e le cose si complicano notevolmente. Tuttavia, il concetto essenziale non cambia.

Ancora più interessante è pensare a cosa succede dall’altra parte della lente. Vi è un raggio che viene piegato di un angolo α’ e che giunge anch’esso in T. In pratica, è facile capire come in queste condizioni semplificate si identificano due punti di concentrazione della luce: uno in direzione S’ e uno in direzione S” (vedi Fig. 4).

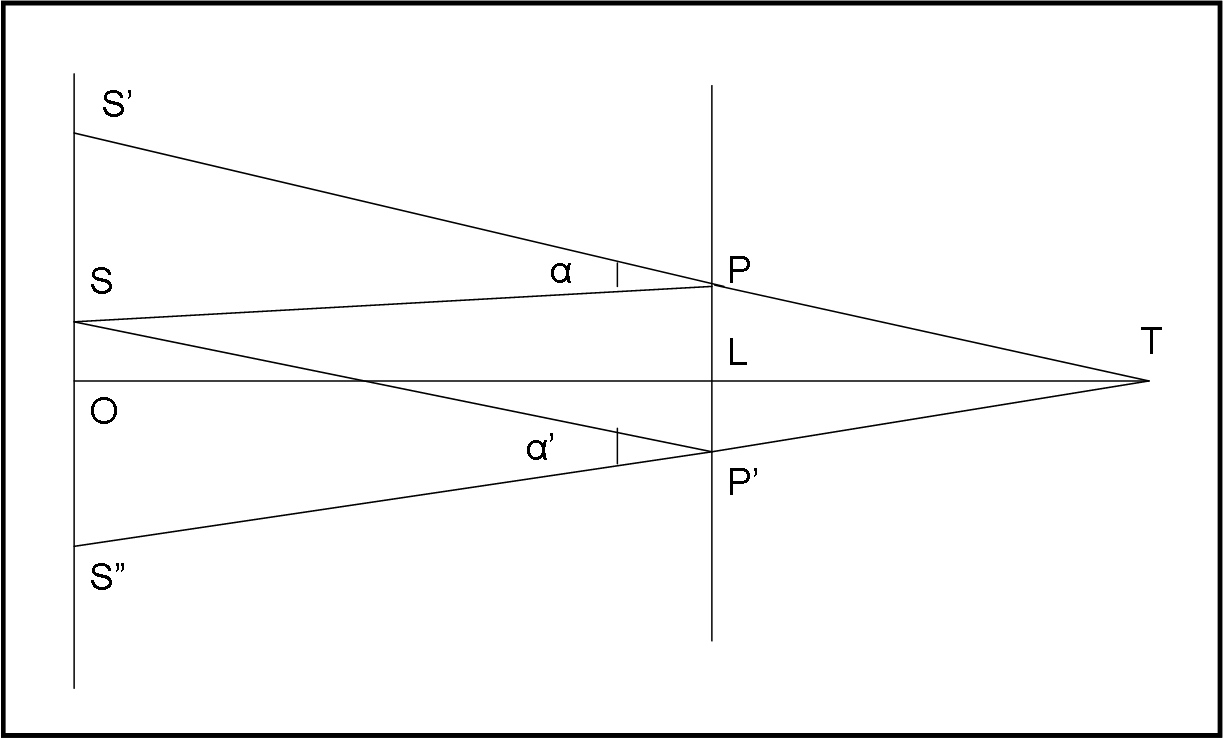
Stiamo dando tanta importanza all’angolo α, ma la ragione è sotto agli occhi di tutti. Quest’angolo è proprio il parametro che stabilisce la deflessione della luce nell’ambito della relatività generale. La formula che lo lega ai parametri fisici della lente è dato da (vedi QUI):

α = 4GM_L/dc²

Tenendo presente la Fig. 1 possiamo scrivere:

α = 4GM_L/dc² = (4GM_L/c²)∙(1/ϑD_L)      …. (2)

Ricordando che:

d ≈ ϑD_L

La (2) lega parametri fisici con l’angolo ϑ che è quello che si osserva direttamente. Inoltre, ci dimostra matematicamente che l’angolo di deflessione diminuisce al crescere della distanza angolare del raggio dalla lente.

Vale la pena fare un piccolo esercizio. Cosa succede se la sorgente è esattamente dietro alla lente, ossia se S è lungo la retta OL? Beh… risulta, ovviamente che β = 0, il che porta a punti simmetrici S’ e S” e, passando alle tre dimensioni, all’anello di Einstein. In altre parole, α = costante e, quindi, per la (2) , anche ϑ = costante.

Questo banale risultato acquista un valore fisico ben più importante qualora si analizzi la situazione in modo più completo. Lo vediamo nelle Fig.re 5 e 6.

 

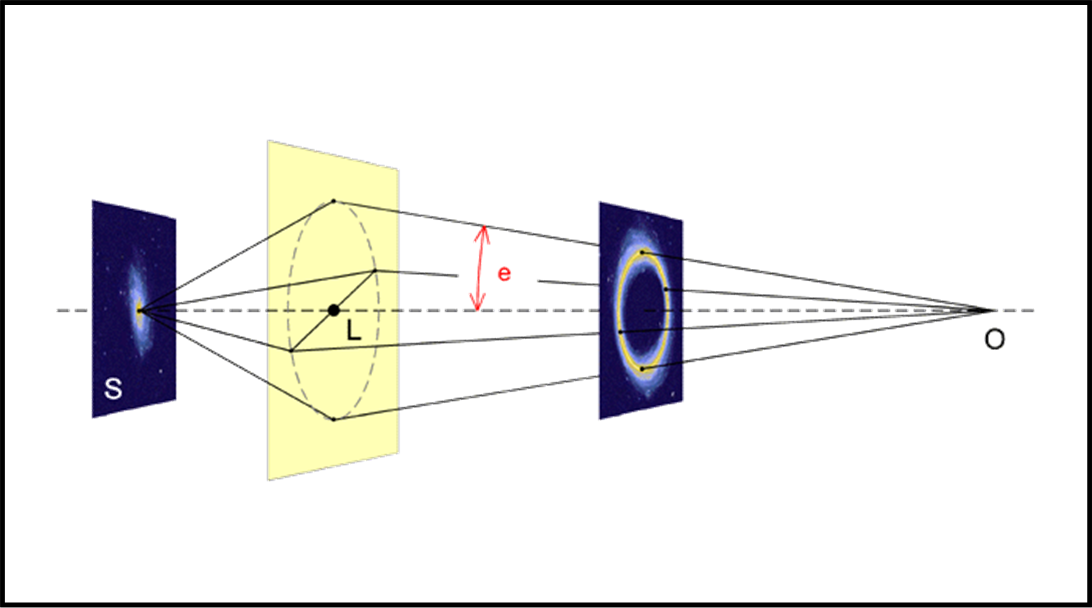
Nella prima abbiamo la sorgente perfettamente allineata, nell’altra invece no. Se poi abbiamo anche una lente allungata si ricade nella celebre croce di Einstein. I calcoli, diventano,ovviamente più complicati. Chi vuole avere un quadro ben più generale può andare QUI.

 

 

 

APPENDICE: Una lente gigantesca

A questo punto non posso non parlare di un risultato eccezionale, ottenuto con una lente veramente gigantesca, l’ammasso galattico Abell 2744. Hubble lo conosce molto bene, dato che è uno tra i migliori "obiettivi naturali"  che può inserire tra lui e le galassie più lontane, ancora immerse nella nebbia dell’era di reionizzazione.

Scrutando in quell’ammasso di massa spaventosa è facile riconoscere immagini relative a oggetti ben più lontani, la cui luce è stata aumentata anche di dieci volte e riesce a raggiungere il nostro amico spaziale. Tutto ciò che sta dietro, prospetticamente, a questa fantastica lente, riesce a mettersi in evidenza con forme più o meno strane: archetti, immagini multiple, cerchi completi. Tutto dipende da quanto l’allineamento sia esatto o no.

Nessuno stupore, quindi, se Abell 2744 ha regalato una nuova galassia, forse la più debole, piccola e lontana.  La geometria relativistica del triangolo sorgente lontana, lente gravitazionale, telescopio non è banalissima. Tanto per farvi capire come mai, chiamate DS la distanza Hubble-sorgente lontana, DA la distanza tra Abell e Hubble e DSA la distanza tra la sorgente e Abell. Anche i bambini direbbero che DS = DA + DSA. E, invece, quando si tratta con distanze cosmologiche questa semplice relazione non è più vera… Non possiamo certo entrare a fondo nelle equazioni che si applicano alla lente gravitazionale, ma potete essere certi che permettono di ottenere un sacco di informazioni.

Tra le tante, però, manca quella più fondamentale: la distanza della sorgente! Per ottenere questo parametro fondamentale per potere inserire la lontanissima sorgente nel giusto periodo evolutivo dell’Universo, ci si affida, normalmente, al redshift e alla legge di Hubble. Purtroppo, le immagini deformate create dalla lente gravitazionale, ben più luminose di quanto sarebbero senza lente,  rimangono estremamente deboli. In poche parole, è ben difficile ottenerne uno spettro che permetta di misurare spostamenti di righe. Bisogna accontentarsi di arrossamento della luce, con gli errori che ne possono derivare, dato che le galassie non nascono tutte gialle o blu… o, meglio ancora, ultraviolette.

Scienziati, un po' esibizionisti, spesso contestano i valori ottenuti in questo modo e riescono anche a pensare che i quasar non siano altro che protuberanze di galassie vicine. Insomma, un bel pasticcio: abbiamo davanti a noi immagini che si riferiscono all’infanzia dell’Universo, all’epoca oscura, immagini che possono svelarci come la luce delle proto galassie abbia riportato la luce, o se volete, abbia  fatto rinascere l’Universo, eppure dobbiamo avere questa incertezza che pesa come un macigno (una delle frasi che la TV ripete fino all’ossessione…).

Dimmi come ti disperdi e ti dirò dove sei

Non si può proprio trovare un metodo alternativo e indipendente per misurare le distanze che ci portano indietro, fino a poche centinaia di milioni di anni dopo il Big Bang? A furia di utilizzare la lente Abell 2744, l’idea è arrivata. Rileggendo attentamente le formule di Einstein si vede che la dispersione delle immagini di una sorgente, creata da una stessa lente, varia in funzione della distanza della sorgente da noi. Non è un’equazione banale, ma esiste. Inoltre, Abell ha permesso di compilare  un vero e proprio elenco di sorgenti più o meno lontane, alcune delle quali, le più vicine, con un valore di distanza piuttosto accurata (la spettroscopia o altre tecniche hanno funzionato).

Bene. Questi valori di distanza, ottenuti in vari modi, possono essere collegati alla dispersione delle immagini causate dalla lente, che rimane sempre la stessa. Si è visto che quanto previsto da Einstein funzionava: più le sorgenti erano vicine e meno disperse erano le immagini create dalla lente. A questo punto bastava estrapolare l’andamento fino alla dispersione osservata per la nuova debole e lontanissima galassia e ricavare la relativa distanza. Insomma, si è costruita una “funzione” sperimentale tra dispersione e distanza e, entrando con la dispersione si è ricavata la distanza. Vedete che le funzioni servono moltissimo… dobbiamo proseguire con la matematica!

Il risultato, veramente straordinario, è che il valore ottenuto in questo modo coincide molto bene con il valore ottenuto soltanto dall’arrossamento. La piccola, eroica galassia ha  un redshift  di z = 10, ossia la sua età non supera  il mezzo miliardo di anni. Un risultato astrofisico enorme, ma anche la prova che ormai si possono usare le lenti gravitazionali come fossero degli obiettivi “normali”. Si può addirittura cambiare il fuoco e focalizzare oggetti più lontani o più vicini.

In ogni modo, il valore di z = 10 ha una sicurezza che è stimata del 95%, un valore mai raggiunto finora. Si conoscono altre galassie primigenie con valori simili, ma la loro l’incertezza è così grande da non dare certezze.

La nuova galassia è veramente piccola (o almeno ciò che manda luce è molto piccolo). Essa misura solo 850 anni luce e ha una massa dell’ordine di 40 milioni di masse solari. Una vera bambina. Il tasso di formazione stellare sembra abbastanza modesto: un Sole ogni tre anni. Sembrerebbe poca cosa se paragonato a quello della Via Lattea (tre volte superiore), ma, se si tiene conto delle dimensioni e del numero di stelle, è invece da considerare molto elevato e il suo contributo allo scioglimento della nebbia circostante è sicuramente all’altezza della situazione.

Dove sono le sorelline?

Insomma, proprio la giusta galassia che ci si aspettava per  quei tempi lontani. Il problema è che dovrebbero essercene tantissime e invece le scoperte sono molto rare. Pensiamo a loro come piccoli ammassi di gas, senza una forma ben definita. Stanno inviando luce e intanto cercano di unirsi in strutture ben più gigantesche. La gravità le aiuta sicuramente. Non dobbiamo disperare, però. La recente scoperta potrebbe essere anche una tra le più grandi delle piccole... e poi è riferita solo a una certa direzione nel cielo. Prima o poi le lenti di Einstein e i nuovi telescopi ne faranno uscire allo scoperto un numero sicuramente enorme. La nebbia si popolerà di luci e l’Universo ci apparirà sempre più popolato e luminoso. Intanto, cerchiamo e utilizziamo tutte le lenti che si trovano in giro, senza discutere molto sul loro prezzo, la loro tecnologia, le loro sigle e i loro codici. Agli astrofisici basta sapere che funzionano!

Articolo originario QUI

 

Il genio di Einstein, un pizzico di fortuna, tanta preparazione ed una buona tecnologia hanno consentito di osservare per la prima volta “in diretta” l’esplosione di una supernova grazie all'effetto lente gravitazionale

QUI e QUI una galassia e una stella lontanissime (la loro luce ha impiegato ben nove miliardi di anni luce per raggiungerci!) osservate grazie all'effetto lente: un risultato questo che, se già è stupefacente per una galassia, ha quasi del "miracoloso" per una piccola stella (più o meno come il nostro Sole) ed è stato reso possibile grazie al perfetto allineamento con un'altra stella, e alle capacità del caro "vecchio" Hubble Space Telescope.