Categorie: Fisica classica
Tags: esplosione Non quiz quiz non quiz razzo
Scritto da: Vincenzo Zappalà
Commenti:1
Un razzo esplode **
Stiamo scherzando parecchio in questi giorni (ma sempre imparando qualcosa). Per chi ha voglia di impegnarsi un pochino di più, ecco un quiz non-quiz di meccanica classica.
Abbiamo imparato come descrivere il moto di un razzo e come il gas di scarico serva a imprimere una variazione di velocità al razzo vero e proprio. Ma non sempre tutti i lanci funzionano alla perfezione. In questo articolo descriviamo un caso abbastanza tipico: l’esplosione del velivolo (fortunatamente senza equipaggio) e ci poniamo un piccolo problema.
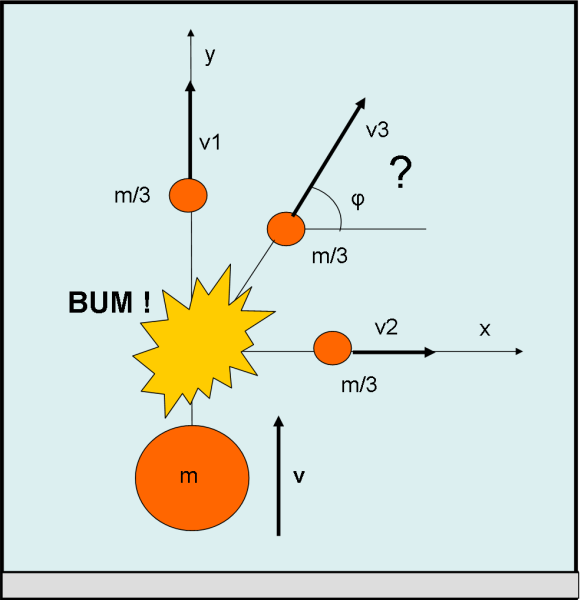
Il razzo di massa m è stato lanciato in direzione perfettamente verticale. Tutto funziona molto bene e in breve esso raggiunge la velocità v. Poi qualcosa accade… avviene una grossa esplosione, dovuta a problemi interni del motore (nessuna meteorite, né detrito spaziale di passaggio).
Caso vuole che il razzo si divida in tre parti di massa uguale (ormai sono tre pezzi di metallo senza motore e senza alcuna spinta data dal gas di scarico). Il primo pezzo prosegue in direzione perfettamente verticale con velocità v1. Il secondo pezzo viene invece sparato a 90° rispetto alla direzione originale del razzo ancora integro (e, quindi, anche del primo pezzo) con una velocità v2
Possiamo calcolare la velocità v3 del terzo pezzo e la direzione del suo moto, oppure ci manca ancora qualche dato?
Come al solito, la risposta è nascosta per dare modo di cercare di risolvere il problema da soli. Per poterla vede, basta cliccare su "mostra la risposta". Ma, fatelo solo dopo averci provato...
RISPOSTA







1 commento
La quantità di moto è una grandezza vettoriale e si deve conservare in assenza di forze esterne.
Inzialmente il vettore vale v m, in modulo ,in direzione verticale.
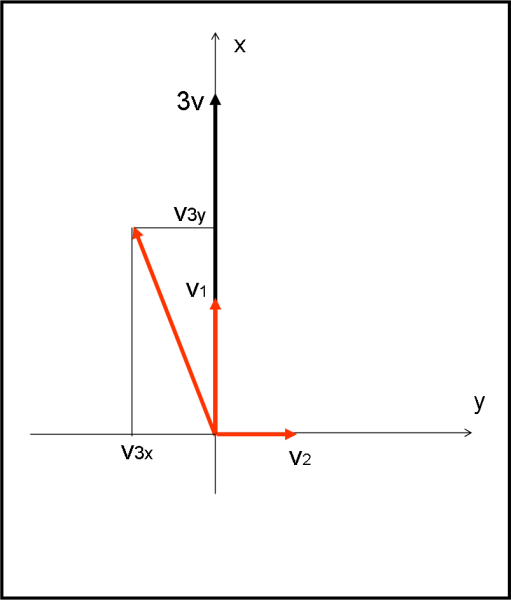
Dopo l'esplosione ci sono 3 componenti
a) v1 m/3 in direzione verticale, verso l'alto
b) v2 m/3 in direzione orizzontale, verso destra
c) v3 m/3 in direzione da calcolare.
Considerando l'asse verticale la quantità di moto mancante verso l'alto (asse y) sarà
v m - v1 m/3 = (v-v1/3) m
Considerando l'asse orizzontale la variazione da compensare verso sinistra (asse x negativo) sarà
- v2 m/3
quindi il terzo pezzo deve compensare una quantità di moto deve avere una direzione
orientata di un angolo
ed un modulo di
radq( (v-v1 /3 )^2 m^2 + v2 ^2 m^2 /9 = radq ( ((v-v1 /3)^2 + v2 ^2 /9 )) m
cioè una velocità verso sinistra pari a