Un gioco all'apparenza molto semplice che, però, può avere risvolti molto interessanti e che permette di spaziare dalla geometria alla fisica e alla matematica. Volendo si potrebbe anche andare oltre...

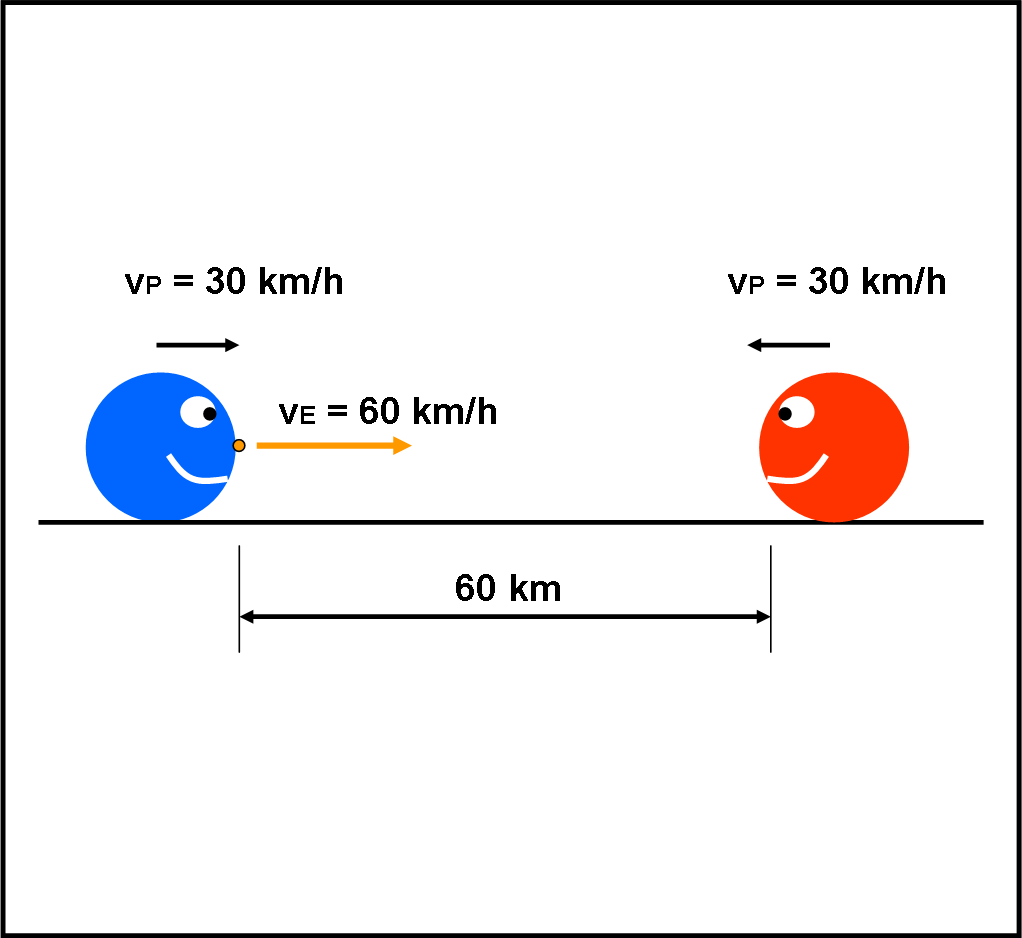
Il gioco è molto semplice e vede due papalatleti che si fronteggiano e che corrono uno verso l’altro, lungo la stessa linea retta, con la stessa velocità v. Sulla fronte di uno di loro viene posto un papalelettrone di dimensioni praticamente nulle. Appena dato il via, i papalatleti si mettono subito in moto con la loro velocità costante, ma il papalelettrone viaggia molto più veloce di loro e, partito dal primo, raggiunge rapidamente il secondo papalatleta. Appena raggiunto, inverte immediatamente la sua corsa e si dirige di nuovo verso il primo papalatleta. Lo raggiunge e inverte nuovamente il suo moto e via dicendo. Un gioco divertentissimo, che dà luogo a un semplice quiz, una volta che si siano impostate le velocità dei papalatleti, la distanza tra di loro e la velocità del papalelettrone.

Ed è proprio quello che vogliamo fare noi. Stabiliamo che la distanza tra i due papalatleti, all’inizio, sia di 60 km. Scegliamo come loro velocità 30 km/ora, mentre quella del papalelettrone è di 60 km/ora. La domanda che ci facciamo è veramente semplice: “Quanti viaggi riesce a fare l’elettrone tra un papallo e l’altro prima che i due papalli si scontrino?”.

La risposta è estremamente semplice e non dipende assolutamente dalle distanze e dalle velocità che abbiamo scelto. L’unica cosa importante è che la velocità del papalelettrone sia maggiore di quella dei due papalli. In queste condizioni possiamo tranquillamente dire che il numero di viaggi che è costretto a fare il papalelettrone è INFINITO. Ogni viaggio, da un papallo all’altro, diventa sempre più corto e dopo un certo tempo, ben determinato, i due papalli si incontrano e quindi anche il papalelettrone è obbligato a fermarsi (anche se ha dimensioni nulle), ma dobbiamo accettare che il numero di tragitti fatti, avanti e indietro, sia infinito.

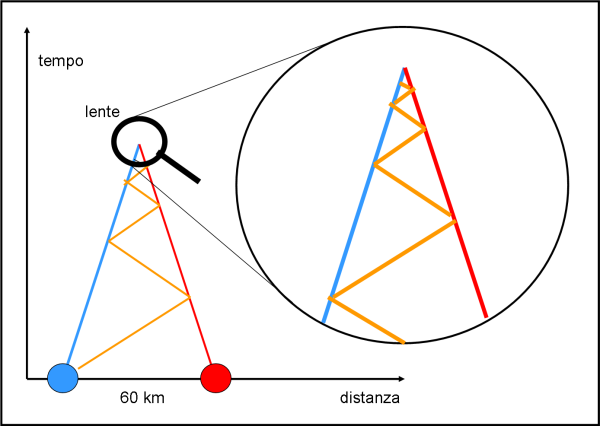
Se disegniamo la distanza dei papalli in funzione del tempo, essa continua a diminuire e il papalelettrone continua a rimbalzare in uno spazio sempre più stretto (Fig. 1). Tuttavia, se utilizziamo una lente e andiamo a vedere cosa succede mentre ci si avvicina all’urto finale dei due papalli, ci accorgiamo che la figura non cambia e l’andamento si ripete fino all’infinito. Siamo di fronte al solito scontro tra zero e infinito, che ci era già servito all’inizio del corso di matematica. Il tratto percorso dal papalelettrone tende a zero (diventa infinitesimo), mentre il numero di tratti percorsi tende a infinito.

Se si riflette un attimo, il gioco dei due papalli ricorda moltissimo il celeberrimo paradosso di Zenone. In quel caso, si dice che se una tartaruga, molto più lenta di Achille piè veloce, parte prima di lui, il grande guerriero greco non riuscirà mai a raggiungerla. Infatti, nel tempo che Achille parte di gran carriera e raggiunge la tartaruga, quest’ultima si è mossa di una certa quantità in avanti. Achille supera in un attimo anche questa piccola lunghezza, ma la tartaruga, nel frattempo, ha proseguito… e via dicendo. In altre parole, la tartaruga è sempre di una quantità, seppure infinitesima, davanti ad Achille. Di questo paradosso ne abbiamo parlato a lungo QUI e QUI.

Il nostro caso papalliano è molto simile, anche se sembrerebbe non esistere un paradosso, dato che il senso comune direbbe che il papalelettrone deve fermarsi dopo un certo numero di viaggi. In realtà, invece, la situazione è analoga: in entrambi i casi dobbiamo tenere conto che aggiungere, a una certa quantità, una quantità sempre più piccola porta a un risultato finale ben determinato e non a infinito.

In altre parole, sommare infinite volte delle quantità sempre più piccole non dà come risultato infinito ma un numero finito.

L’assurdità dei due papalli che si urtano  sta proprio nell’accettare che per ottenere la fermata del papalelettrone è necessario che questo rimbalzi infinite volte, anche se in un tempo sicuramente limitato.

Cerchiamo di capire meglio questa apparente assurdità. Se io dicessi: “Contate ogni volta che il papalelettrone tocca uno dei due papalli”, voi comincereste a contare: “Uno, due, tre, quattro, ecc., ecc.” in attesa che tutto finisca.

Vi accorgereste però che il numero continua a salire e non ha mai fine. Vi arrabbiereste non poco dicendo: “E’ impossibile! Se continuo a sommare tragitti, ossia intervalli di tempo, per un  numero infinite di volte, l’elettrone deve automaticamente impiegare un tempo infinito per terminare la sua corsa". E, invece, vediamo benissimo che dopo un certo tempo ben definito, che dipende SOLO dalla distanza e dalla velocità dei papalli, la corsa deve avere termine.

L’errore che si commette è lo stesso di Achille e la tartaruga. Voi non  sommate quantità costanti, ma quantità sempre più piccole di quella precedente. In  questo caso, ribadiamo ancora, un numero infinito di volte una quantità che tende a diventare zero dà come risultato un valore finito e non infinito. Non dovreste contare “uno, due, tre, quattro,…” sempre alla stessa velocità, come se fossero secondi di tempo, ma dovreste contare accelerando le parole, dato che l’intervallo di tempo di ogni tragitto si fa sempre più corto e tende a diventare zero.

Vi sono vari modi per dimostrare in modo analitico questo fatto (lo avevamo già fatto per il paradosso di Zenone) e per andare avanti con le domande e le risposte, tipo: quanta strada ha percorso il papalelettrone prima di rimanere incastrato tra i due papalli? E ancora: cosa succede se le dimensioni del papalelettrone non sono nulle?

Il giochino diventa un ottimo strumento didattico per analizzare la situazione generale (velocità e distanze qualsiasi) sia con mezzi puramente matematici e/o geometrici (normalmente più rapidi), sia attraverso gli sviluppi in serie, magari non indispensabili, ma interessanti per  comprenderne appieno il significato.

Usiamo un po' di fisica 

In parole più tecniche, gli intervallini di tempo tra un incontro e l’altro possono essere rappresentati da una serie di infiniti termini che converge verso un valore finito.

Ricordiamoci che capire le situazioni come quella del paradosso di Zenone o dell’elettrone di Papalla è un punto fondamentale per comprendere molti altri concetti matematici come il limite, l’infinitesimo, l’infinito, lo sviluppo in serie e la geometria analitica in generale. Seguiamo quindi da vicino le peripezie dei due papalli e del simpatico e disponibile papalelettrone…

Iniziamo col descrivere il campo da gioco e tutto ciò che si può dedurre prima dell’ingresso del papalettrone. Utilizziamo la Fig. 1, decisamente più “seria” e adatta ai calcoli matematici (veramente ridicoli…). Impostiamo il tempo come asse orizzontale e lo spazio percorso come asse verticale.

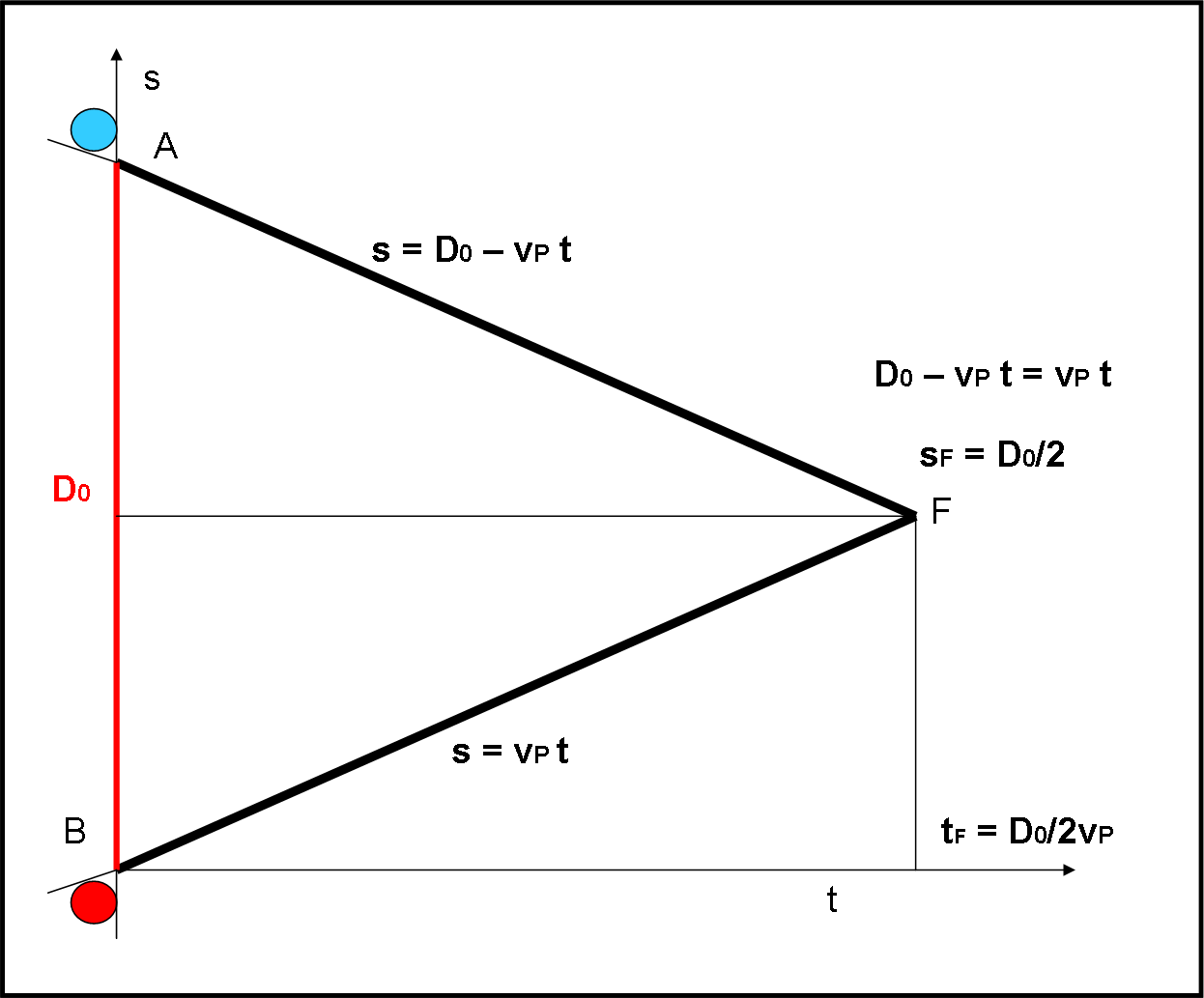
I due papalli partono con una distanza relativa D₀ e viaggiamo ognuno con una velocità v_P. Le loro traiettorie, al passare del tempo, sono descritte dalle due rette inclinate, che hanno equazioni:

s = v_P t

e

s = D₀ - v_Pt

Negli assi tempo e spazio, queste rette rappresentano le equazioni del moto, ossia lo spazio percorso in funzione del tempo con una velocità v_P.

Risulta immediato trovare il punto in cui esse si intersecano, ossia dove i due papalli si scontrano: basta eguagliare la s, ossia lo spazio percorso dai due papalli.

Uguagliando le due relazioni di prima, si ottiene:

v_P t  = D₀ - v_Pt

Da cui si ricava il valore t_F che ci dice l’istante in cui si scontrano i due papalli:

v_P t_F  = D₀ - v_Pt_F

2 t_F v_P = D₀

t_F = D₀/2v_P

Conosciuto t_F e ancora più immediato trovare lo spazio percorso da ciascun papallo prima dell’incontro finale. Basta sostituire t_F in una qualsiasi delle due rette precedenti e si ha:

s_F = v_P t_F = v_PD₀/2v_P = D₀/2

s_F = D₀ – v_Pt_F = D₀ – v_PD₀/2v_P = D₀ – D₀/2 = D₀/2

Abbiamo svolto calcoli di una banalità estrema. La conclusione è ovviamente semplicissima: quando i due papalli si incontrano hanno percorso lo stesso spazio, che è esattamente uguale alla metà della distanza iniziale.

Una piccola riflessione: se cambiassimo le velocità dei due papalli (mantenendole, però, uguali e contrarie) o modificassimo la distanza tra loro due, cambieremmo sicuramente il tempo dell’incontro (d’altra parte t_F dipende sia da D₀ che da v_P), ma non cambiamo il punto d’incontro che avviene sempre e comunque a metà strada dai punti di partenza.

Se cambiassimo anche i moduli delle velocità dei due papalli, ossia le loro velocità fossero opposte ma non uguali, la faccenda si complicherebbe un poco: cambierebbe il tempio dell’incontro e la distanza percorsa dai due papalli… Per adesso limitiamoci al nostro caso semplificato. Un domani chissà…

Un’altra grandezza estremamente importante che possiamo studiare nella Fig. 1 è la distanza, istante per istante, tra i due papalli. Chiamiamola D_i, in Fig. 2. Ovviamente, per quanto detto finora questa distanza vale D₀ alla partenza e vale ZERO alla fine (i due papalli si scontrano).

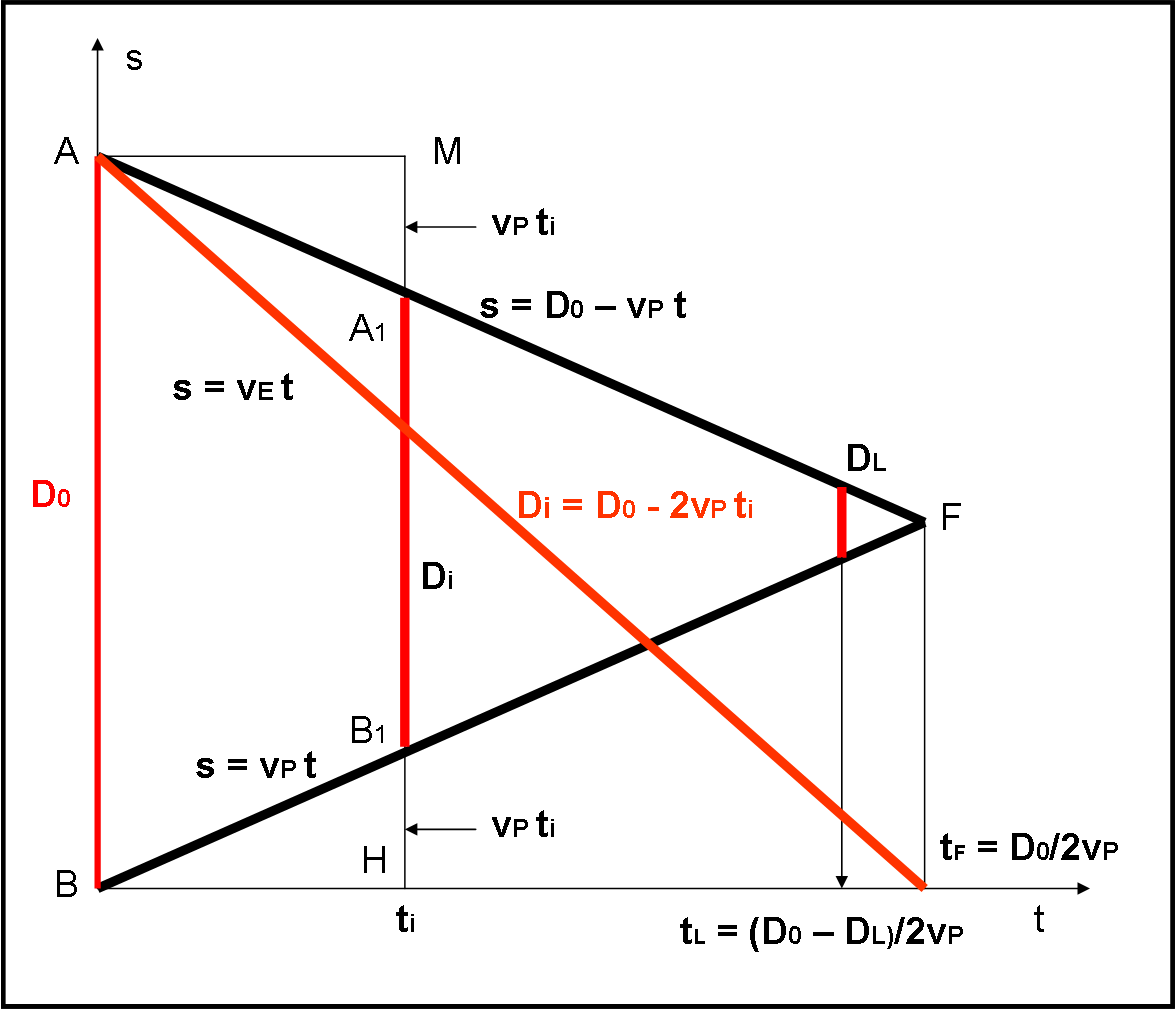
Questa distanza variabile deve essere funzione solo e soltanto del tempo (e della velocità v_P). Essa si ricava facilmente scegliendo un certo t_i e scrivendo la differenza tra le posizioni s_i1 e s_i2 dei due papalli.

Al tempo t_i il primo papallo è arrivato in

s_i1 = D₀ – v_Pt_i

e il secondo in

s_i2 = v_Pt_i

Facendo la differenza tra s₁ e s₂, ricaviamo la distanza relativa Di tra i due papalli a un qualsiasi tempo ti:

D_i = D₀ – v_Pt_i – v_Pt_i = D₀ – 2v_Pt_i     …. (1)

La conclusione si può ottenere guardando direttamente la figura e notando che la differenza tra D₀ e D_i è proprio data dalla somma dei due segmenti uguali B₁H e A₁M, dati proprio da v_Pt_i…

In ogni modo abbiamo ricavato la funzione D(t) che, per un certa velocità impostata in partenza, descrive la variazione della distanza tra i due papalli in funzione del tempo. La possiamo rappresentare nella stessa Fig. 2, come la linea colorata in rosso. Essa è una retta che parte da (D₀,0) e arriva in (0,t_F).

Questa relazione ci permette di ricavare immediatamente (sia matematicamente che geometricamente) il valore di D_i, sapendo il tempo t_i o, cosa che potrebbe anche essere più interessante, il viceversa, ossia ricavare il tempo t_i,impostando un certo valore della distanza D_i tra i papalli. Se pensiamo che l’elettrone, che introdurremo tra poco, potrebbe avere anche un diametro DL, noi poniamo un limite alla distanza relativa raggiungibile dai due papalli e questo è dato proprio da DL, dato che l’elettrone rimarrebbe incastrato tra i due papalli. Il valore DL ci permette subito di sapere il tempo che è passato per arrivare all’incastro… Lasciamo questa eventualità da parte e introduciamo finalmente il papalelettrone di diametro nullo. Il problema è essenzialmente matematico e introdurre parametri fisici avrebbe ben poco interesse.

Passiamo alla matematica

Abbiamo ricavato tutto il ricavabile dalla Fig. 1, tra cui una conclusione che appare ovvia ma che sarà fondamentale nel prosieguo dl gioco: il tempo di incontro è un valore finito e facilmente determinabile. I due papalli  a un certo tempo t_F si scontrano e tra di loro non vi è nemmeno un posticino per l’elettrone per piccolo che sia. Ne segue che anche lo spazio percorso avanti e indietro dall’elettrone deve non solo terminare, ma avere anche un valore finito.

Prima di rappresentarlo nella figura, che abbiamo già cominciato a conoscere, facciamo un semplice ragionamento su quello che succede. L’elettrone deve muoversi all’interno del triangolo delle figure precedenti, in quanto appena tocca un papallo deve tornare indietro. La sua velocità v_E è per definizione maggiore di v_P (se non lo fosse rimarrebbe attaccato al primo papallo…). Ciò comporta che la traiettoria del papalelettrone è composta da tanti tratti più inclinati dei bordi del triangolo. Più inclinati vuol dire che per un qualsiasi istante t, pur vicinissimo a t_F, il papalettrone riesce sempre a “staccare” il papallo superiore o inferiore e raggiungere l’altro.

Possiamo fare diventare la differenza tra t e t_F piccola a piacere, ma continuiamo ad avere sempre una stessa figura con il zig-zag del papalelettrone sempre attivo. Ciò che diminuisce sempre più è il tragitto compiuto tra i due papalli. Dato che esiste sempre un t_F - t_i più piccolo di una certa quantità piccola a piacere, esiste sempre un tragitto dell’elettrone tra i due papalli. In altre parole, il numero di intervallini sempre piccoli di tempo è uguale a infinito e tale deve essere anche il numero di viaggi.

La prima domanda del nostro quiz originario non dipende, perciò, dai dati di partenza: qualsiasi siano D₀, v_P e v_E, i tragitti percorsi dal papalelettrone sono infiniti, proprio come erano infiniti gli intervallini di spazio a cui la tartaruga di Zenone lasciva Achille dietro di sé. L’errore è pensare che la somma di un numero infinito di intervalli sia anch’esso un numero infinito. Se gli intervalli sono sempre più piccoli e tendono a diventare zero, la somma può benissimo tendere a un valore finito. In parole più tecniche, una serie di termini via via più piccoli ha come risultato un valore finito. Ricordate la serie geometrica? Bene siamo nella stessa situazione.

Come succedeva per Achille e la tartaruga, la faccenda ha poi anche una conclusione “fisica”. Così come il piede di Achille non aveva dimensioni nulle, così succede anche al papalettrone, per cui, in realtà il numero di viaggi del papalettrone (di diametro diverso da zero) è un numero finito che si può ricavare abbastanza facilmente. Forse dovevamo considerare un fotone… ma ci saremmo scontrati con la sua massa relativistica e la conclusione sarebbe stata simile, anche se ben più complicata.

Bene, quanto detto a parole cerchiamo di dimostrarlo attraverso la matematica e la geometria, introducendo la Fig. 3

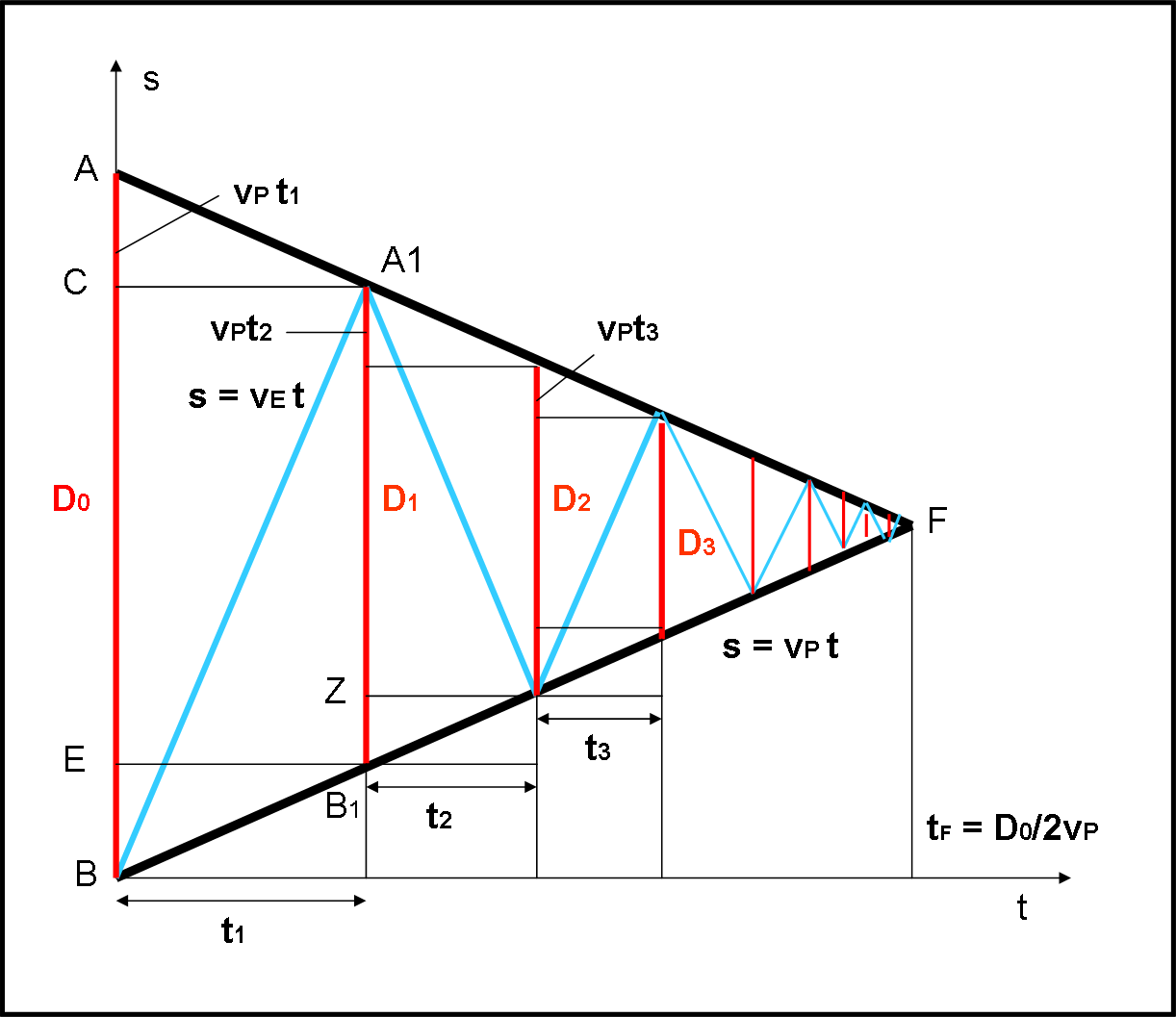
Aggiungiamo alla solita figura “triangolare”, la linea azzurra che descrive il percorso fatto dall’elettrone. Lui parte, ad esempio, dal papallo B (ma potevamo farlo partire da A, non cambiava assolutamente niente). La sua legge del moto è data da:

s = v_E t

A noi interessa sapere a quale istante t₁ esso incontra il papallo A che si muove con la legge:

s = D₀ – v_Pt

Si ottiene subito :

t₁ =D₀/(v_E + v_P)

Notiamo che la stessa relazione si ottiene subito guardando la figura. D₀ non è altro che la somma dei due segmenti AC e CB, dato che  essi valgono:

AC = v_Pt

CB = v_Et

Si può scrivere:

D₀ = AC + BC = v_Pt + v_Et

Da cui, nuovamente:

t₁ = D₀/(vE + vP)

Non stupiamoci di certo… in fondo, abbiamo applicato sempre e soltanto le stesse relazioni.

Nel primo caso abbiamo eseguito l’intersezione tra due rette; nel secondo abbiamo sommato due segmenti, ma il succo rimane lo stesso: geometria e matematica vanno sempre a braccetto. Quale usare è una nostra scelta (basta non commettere errori).

Facciamo anche in fretta a calcolare la distanza tra i due papalli (D₁) al momento del primo incontro, ossia all’istante t₁.

La calcoliamo con un’altra relazione, indipendente dalla prima, ma che faccia uso sempre di t₁:

D₁ = D₀ – AC – EB = D₀ - 2 v_Pt₁       …. (2)

Una relazione che avevamo, ovviamente, già incontrato, essendo nient’altro che la (1), dove B₁H è proprio uguale a EB e A₁M è uguale ad AC. Come sempre, meglio abbondare…

Sostituendo t₁ nella (2), abbiamo:

D₁ = D₀ - 2v_PD₀/(v_E + v_P) = D₀(1 – 2v_P/(v_E + v_P)) = D₀(v_E + v_P – 2v_P)/(v_E + v_P)

D₁ = D₀(v_E – v_P)/(v_E + v_P)

Ricaviamo adesso t₂, partendo dal valore D₁ che già conosciamo. Come già ricordato prima, anche in questo caso, risulta immediatamente che il segmento D₁ è uguale alla somma A₁Z e B₁Z, per cui.

D₁ = v_P t₂ + v_E t₂

t₂ = D₁/(v_E + v_P) = D₀(v_P - v_E)/((v_E + v_P)(v_E + v_P))

t₂ =  (D₀/(v_E + v_P)) (v_E - v_P)/(v_E + v_P)

Non abbiamo eseguito il prodotto al denominatore, dato che D₀/(v_E + v_P) compariva anche in t₁…

Non ci resta che calcolare D₂ (in modo del tutto analogo a quanto fatto per D₁, come si vede bene dalla figura):

D₂ = D₁ – 2v_Pt₂ = D₁ – 2v_PD₁/(v_E + v_P) = D₁(1 – 2v_P/(v_E + v_P)) = D₁(v_E – v_P)/(v_E + v_P)

D₂ = D₀(v_E – v_P)²/(v_E + v_P)²

Ricaviamo, nuovamente, t₃ partendo dal valore D₂ che abbiamo appena calcolato:

D₂ = v_P t₃ + v_E t₃

t₃ = D₂/(v_E + v_P) = (D₀/(v_E + v_P)) ((v_E – v_P)²/(v_E + v_P)²)

Ovviamente, avremo poi:

D₃ = D₀(v_E – v_P)³/(v_E + v_P)³

e via dicendo…

Abbiamo sufficienti termini per generalizzare il risultato relativo a D_i e t_i

D_i = D₀(v_E – v_P)ⁱ/(v_E + v_P)ⁱ

t_i = (D₀/(v_E + v_P)) ((v_E – v_P)^i-1/(v_E + v_P)^i-1)

Occupiamoci subito di t_i. Per trovare il tempo totale che il papalettrone impiega per terminare il suo percorso, basta che sommiamo tutti gli intervallini che, ovviamente, sono infiniti.

t_F = Σ^∞_n=1(D₀/(v_E + v_P)) ((v_E – v_P)^n-1/(v_E + v_P)^n-1)

t_F = D₀/(v_E + v_P) Σ^∞_n=1 ((v_E – v_P)/(v_E + v_P))^n-1

Ma questa non è altro che una serie geometrica, dato che il rapporto tra due termini consecutivi è costante. Oltretutto, il termine della serie risulta essere sempre minore di uno, infatti il denominatore è chiaramente maggiore del numeratore. Stiamo proprio sommando quantità che diventano sempre più piccole.

Noi conosciamo molto bene, dai capitoli relativi in matematica, la somma dei termini di una serie geometrica del tipo:

Σ^∞_n=0 xⁿ = 1/(1- x)

Nel nostro caso:

t_F = Σ^∞_n=1 t_n = D₀/(v_E + v_P)Σ^∞_n=1 ((v_E – v_P)/(v_E + v_P))^n-1 = D₀/(v_E + v_P) (1/ (1 – ((v_E – v_P)/(v_E + v_P))))

t_F = D₀/(v_E + v_P) ((v_E + v_P)/ 2v_P) = D₀((v_E + v_P)/(v_E + v_P))/ 2v_P

t_F = D₀/2v_P

Non possiamo certo sorprenderci se abbiamo trovato esattamente il valore del tempo di incontro tra i due papalli! Questo è proprio il tempo necessario perché l’elettrone di diametro nullo si incastri tra i due papalli, ossia il tempo del loro contatto.

Un lavoro inutile? No di certo. Innanzitutto, abbiamo visto che sono necessari infiniti viaggi per giungere alla conclusione, come indica il valore di n che va proprio da uno a infinito. Ogni valore successivo di n indica proprio un tragitto in più fatto da un papallo all’altro. E poi… ci siamo divertiti a trovare una bellissima serie geometrica, che ci permette di risolverne subito un’altra…

Rimane, infatti, aperta la domanda: “Quanta strada deve fare il papalelettrone per arrivare alla fine della corsa?”. Benché lui sia comunque costretto a fare infiniti viaggi avanti e indietro, cambia  il percorso effettuato in base alla sua velocità v_E. Più è alta e più strada deve percorrere.

Introduciamo, allora, una nuova distanza nella figura precedente, il tratto verde S_i, come mostrato in Fig. 4.

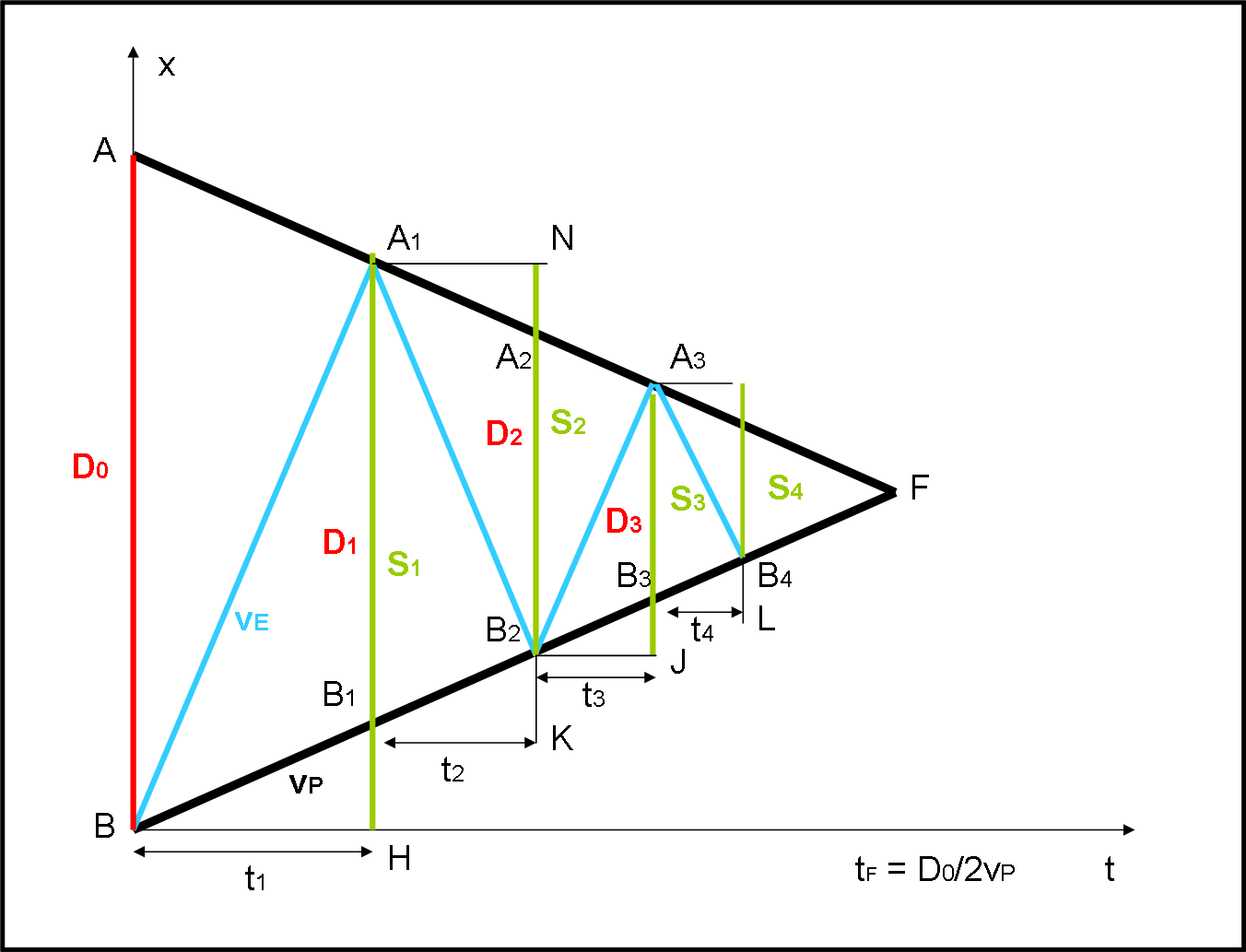
Risulta chiarissimo che i tratti verdi S_i rappresentano lo spazio percorso durante ogni intervallo ti.

Possiamo scrivere la relazione ricorrente:

S₁ = v_E t₁

S₂ = v_E t₂

S₃ = v_E t₃

…

S_i = v_E t_i

E’ solo e soltanto una questione di triangoli…

Ne segue che per avere la somma totale degli Si basta fare la somma totale di v_Et_i. In tal modo avremo lo spazio totale percorso dal papalelettrone, in moto con velocità v_E.

Basta scrivere:

S_TOT = Σ^∞_n=1S_n = vE Σ^∞_n=1t_n = v_E t_F = D₀v_E/2v_P

Avevamo bisogno di applicare il risultato della serie trovata attraverso i tempi? Assolutamente no. Potevamo trovare la risposta direttamente dalla figura. Ragioniamoci un attimo sopra.

Quando l’elettrone arriva in A₁, torna indietro effettuando il tratto azzurro con la stessa velocità di prima. Il tratto percorso potrebbe essere aggiunto SOPRA quello precedente (dobbiamo sommarli, senza interessarci se lo compie verso l’alto o verso il basso). Basta, quindi, traslare B₂N verso l’alto fino a che B₂ sia alla stessa altezza di A₁. La stessa cosa può essere fatta per S₃, ossia per JA₃, che va inserito sopra quello precedente, con J alla stessa altezza della posizione attuale di N. Alla fine, facendo questo gioco di  “costruzione”, troviamo esattamente S_TOT. Quando? Beh… esattamente quando saremo arrivati in t_F! La linea che tocca tutti gli estremi dei segmenti verdi traslati in questo modo è una retta la cui pendenza è data da v_E (per definizione). Si ottiene così il triangolo BST come mostrato in Fig. 5.

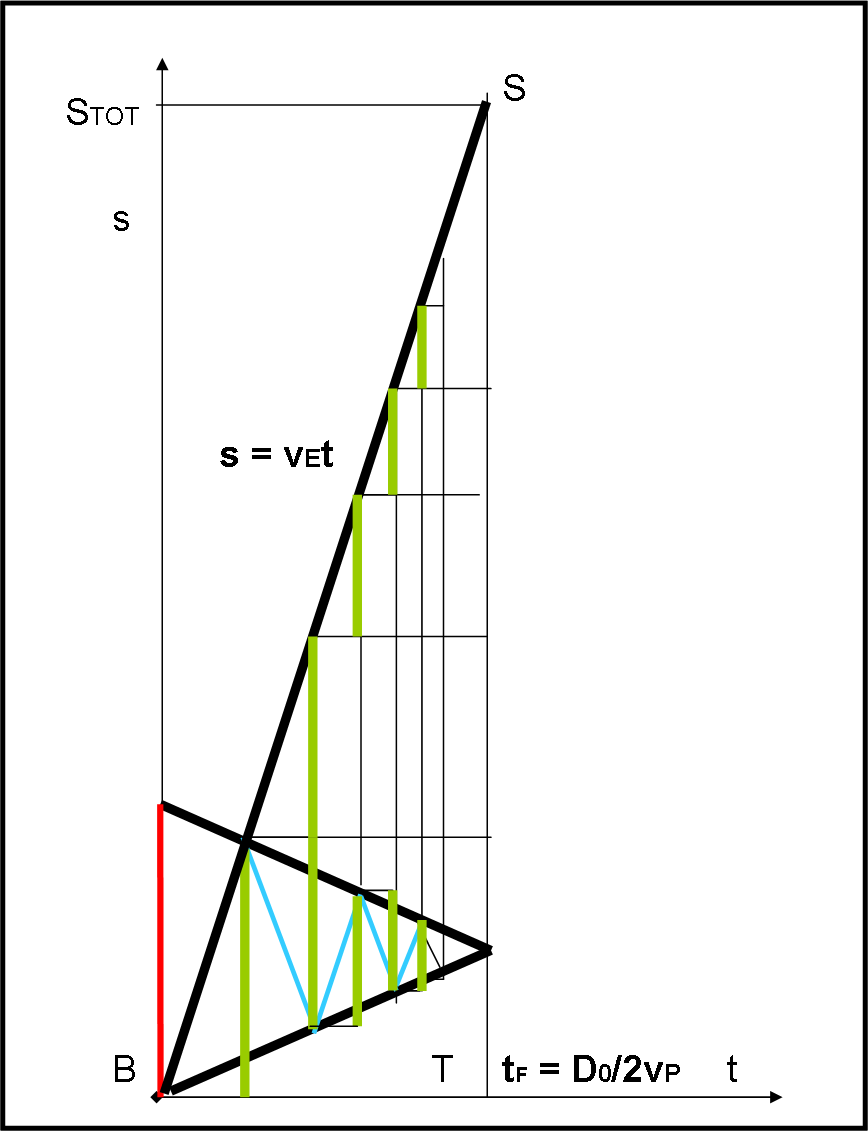
L’altezza S_TOT è quindi data immediatamente da:

S_TOT = t_F v_E = D₀v_E/2v_P

Cosa si può fare graficamente? Tracciare la retta da B inclinata di v_E e fermarla quando incontra la perpendicolare tracciata all’asse t dal punto t_F (v_E e t_F sono noti). L’altezza del triangolo, così trovato, indica subito la lunghezza del tragitto percorso dall’elettrone.

Si può anche fare in altro modo… Vi ricordate quei “metri” di legno pieghevoli che usavano i falegnami? Bene, la linea azzurra che indica il cammino del papalelettrone assomiglia proprio a quell’antico strumento (io lo uso ancora…). L’unica differenza è che le varie aste sono di lunghezza decrescente. Servirebbe a poco come misuratore di lunghezze, ma è perfetto per il nostro problema.

L’unica cosa che dobbiamo fare è “aprirlo” del tutto. Per come è costruito, i vari tratti del metro formano sempre angoli uguali con l’asse dello spazio (la velocità del papalelettrone è sempre la stessa sia che vada verso l’alto o verso il basso). Ne segue che possiamo piegare il metro e farlo diventare rettilineo mantenendo le lunghezze dei singoli tratti, come descritto nella Fig.6.

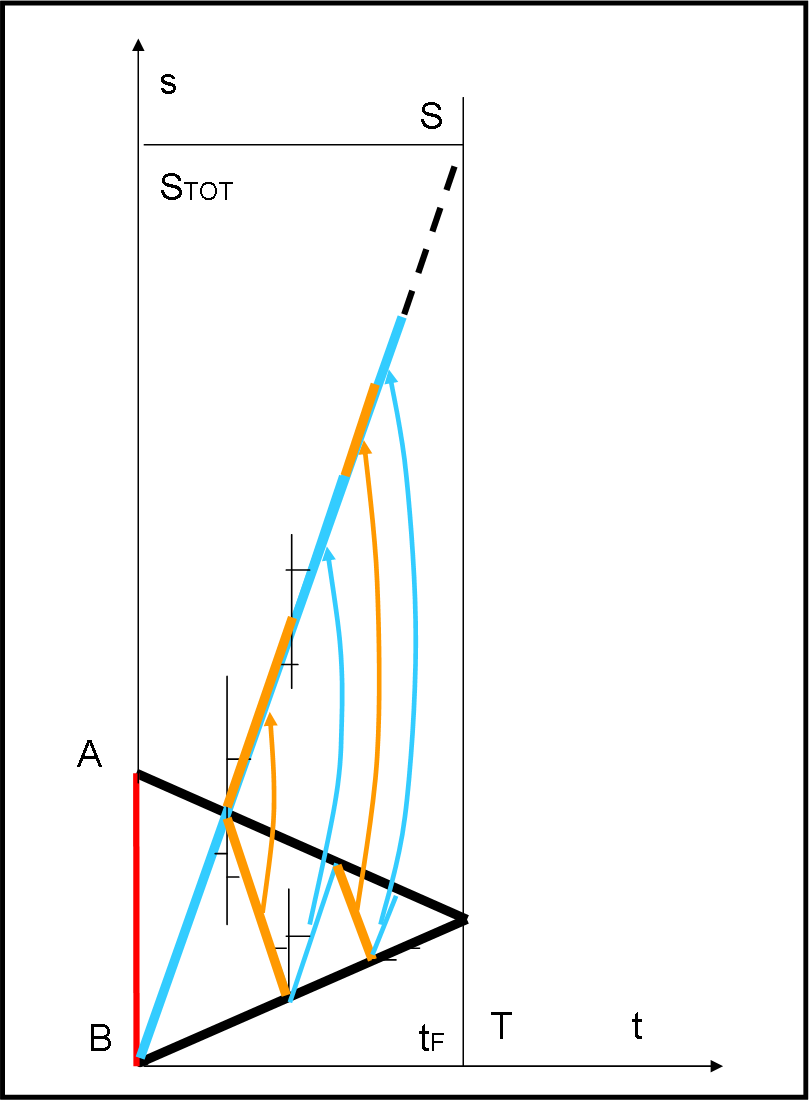
Questo segmento rettilineo ha quindi come lunghezza totale i tragitti del papalelettrone. Ne segue immediatamente lo stesso triangolo della Fig. 5 e quindi la distanza percorsa dalla nostra simpatica particella.

Ognuno è libero di usare il sistema che preferisce, dato che sono in pratica la stessa identica cosa e che danno luogo allo stesso risultato. In un modo o nell’altro, comunque, ci siamo divertiti con qualche intersezione tra rette, qualche sviluppo in serie e un metro da falegname un po’ speciale. E dite poco? Questi papalliani sono proprio fantastici e la matematica insieme alla sua amica geometria sono proprio divertenti!